Functions and algebra: Use a variety of techniques to sketch and interpret information from graphs of functions
Unit 9: The cosine function
Dylan Busa
Unit 9 outcomes
By the end of this unit you will be able to:
- Sketch functions of the form [latex]\scriptsize y=a\cos k\theta[/latex].
- Determine the effects of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex] on the cosine graph of the form [latex]\scriptsize y=a\cos k\theta[/latex].
- Find the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex] from a given cosine graph of the form [latex]\scriptsize y=a\cos k\theta[/latex].
Remember that the domain of trigonometric functions can be represented as [latex]\scriptsize x[/latex] or [latex]\scriptsize \theta[/latex]. Therefore, [latex]\scriptsize y=\cos x[/latex] and [latex]\scriptsize y=\cos \theta[/latex] are the same function.
What you should know
Before you start this unit, make sure you can:
- Sketch cosine functions of the form [latex]\scriptsize y=a\cos \theta +q[/latex]. Refer to level 2 subject outcome 2.1 Unit 5 if you need help with this.
Introduction
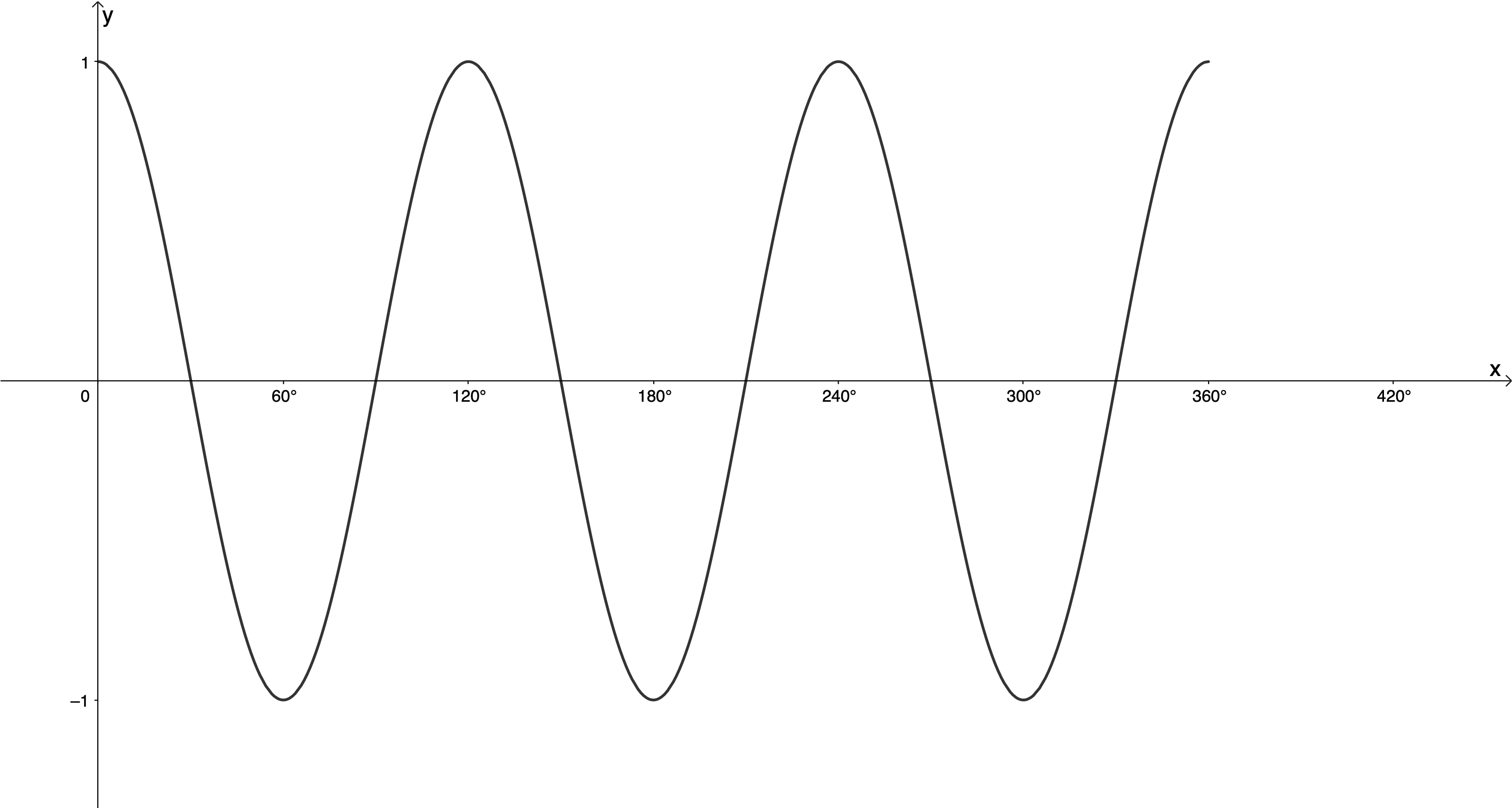
We know that the period of the cosine function is [latex]\scriptsize {{360}^\circ}[/latex] (same as the sine function) (see Figure 1).
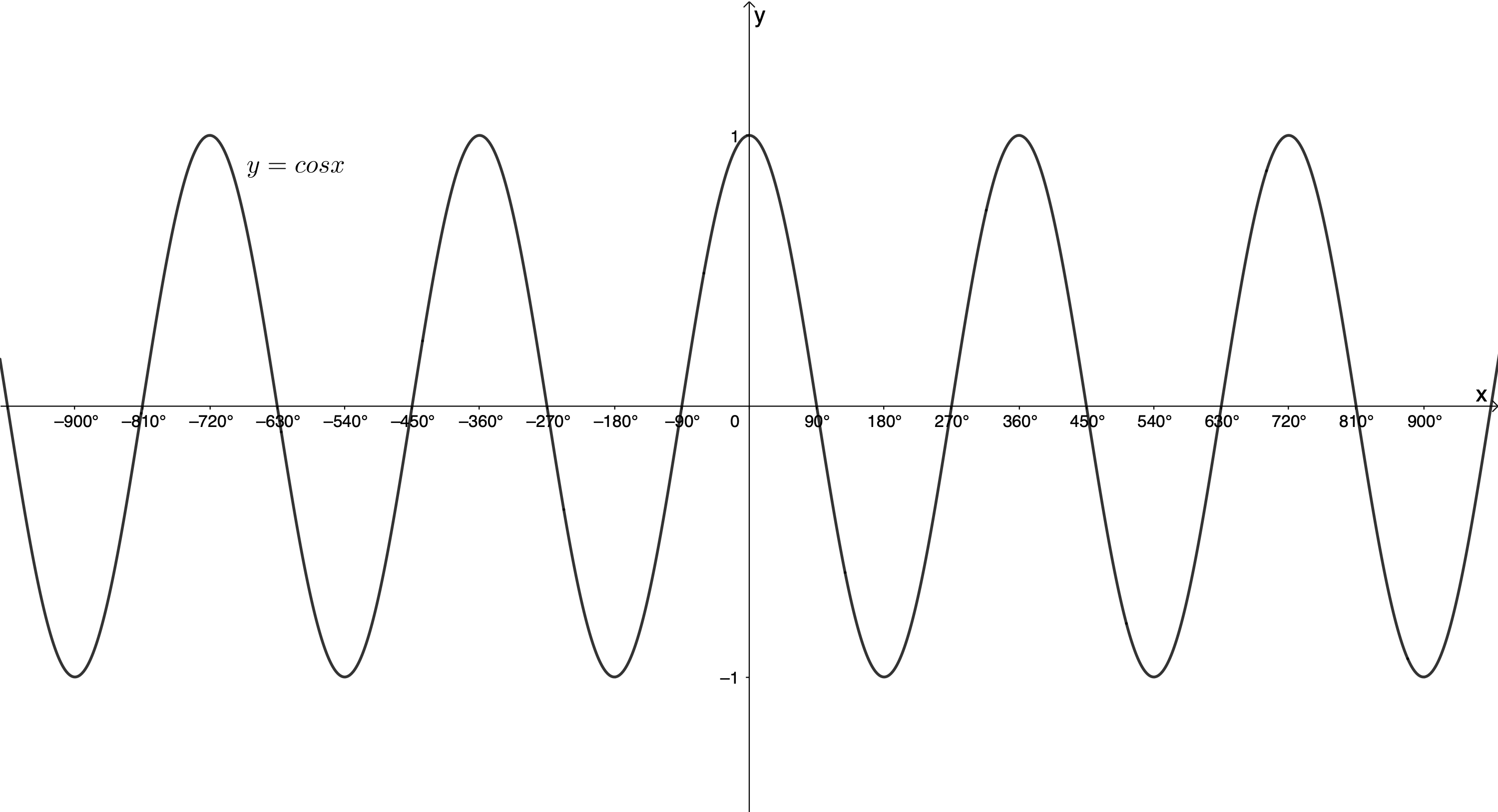
We also know that the amplitude is the maximum distance of the function from its midpoint and that the amplitude of [latex]\scriptsize y=\cos x[/latex] is [latex]\scriptsize 1[/latex] (see Figure 2).
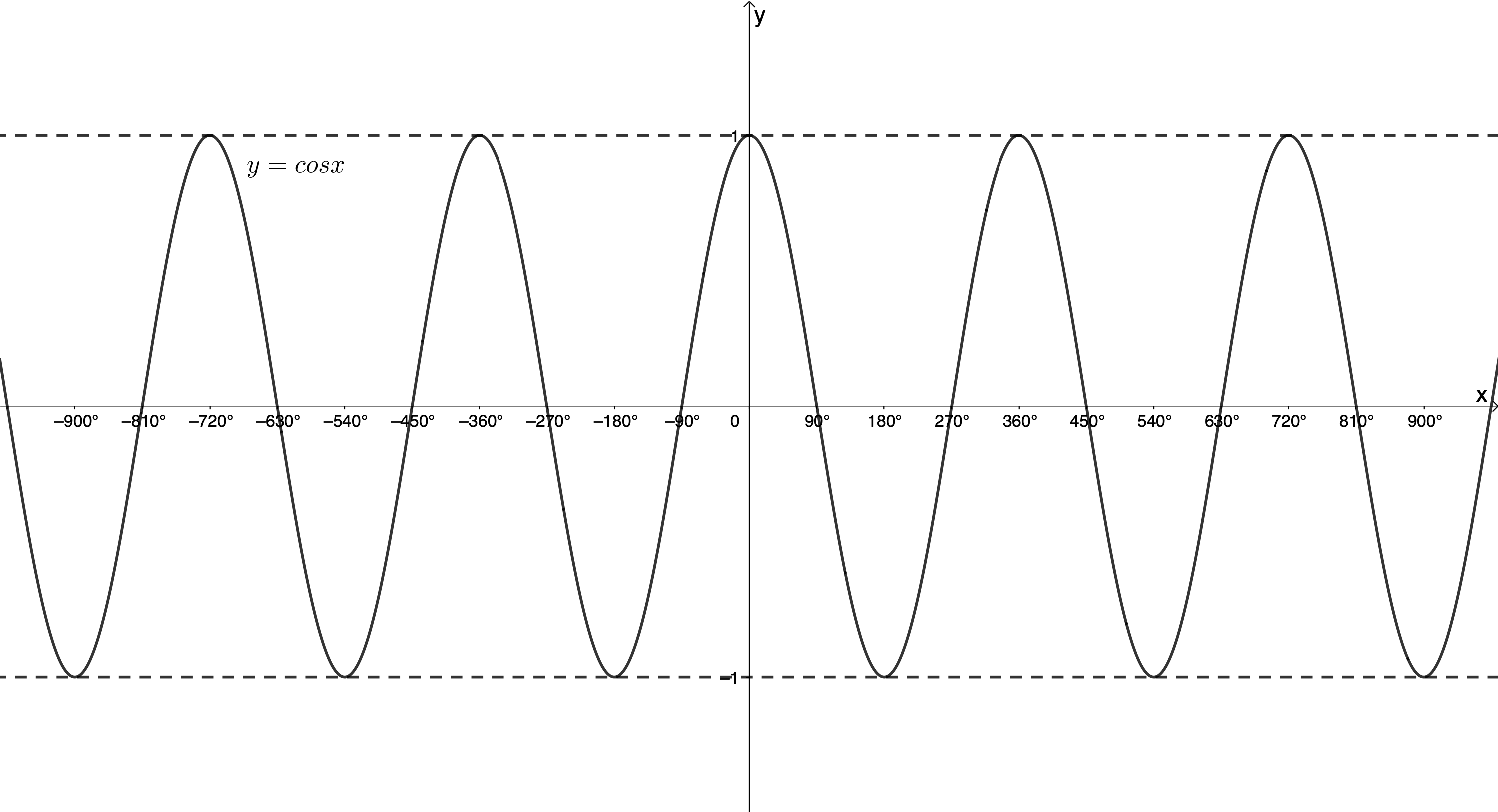
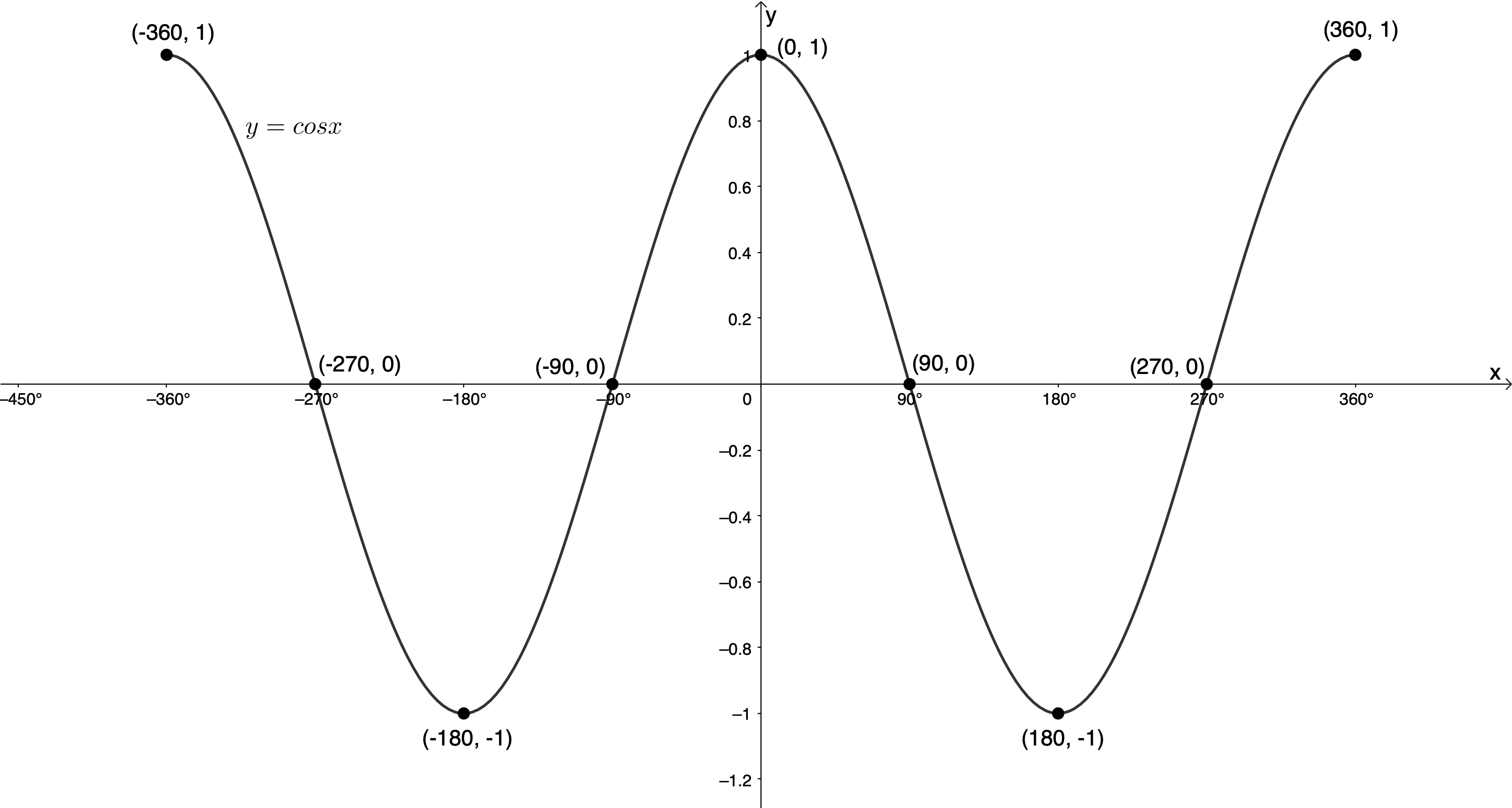
In [latex]\scriptsize y=\cos x[/latex], because the amplitude is [latex]\scriptsize 1[/latex] and the graph’s midpoint is the x-axis, the maximum value of [latex]\scriptsize y=\cos \theta[/latex] is [latex]\scriptsize 1[/latex] and the minimum value is [latex]\scriptsize -1[/latex]. In the interval [latex]\scriptsize {{0}^\circ} \leq x \leq {{360}^\circ}[/latex], the graph of [latex]\scriptsize y=\cos x[/latex] has a maximum turning point at [latex]\scriptsize ({{0}^\circ},1)[/latex] and [latex]\scriptsize ({{360}^\circ},1)[/latex], and a minimum turning point at [latex]\scriptsize ({{180}^\circ},-1)[/latex] (see Figure 3).
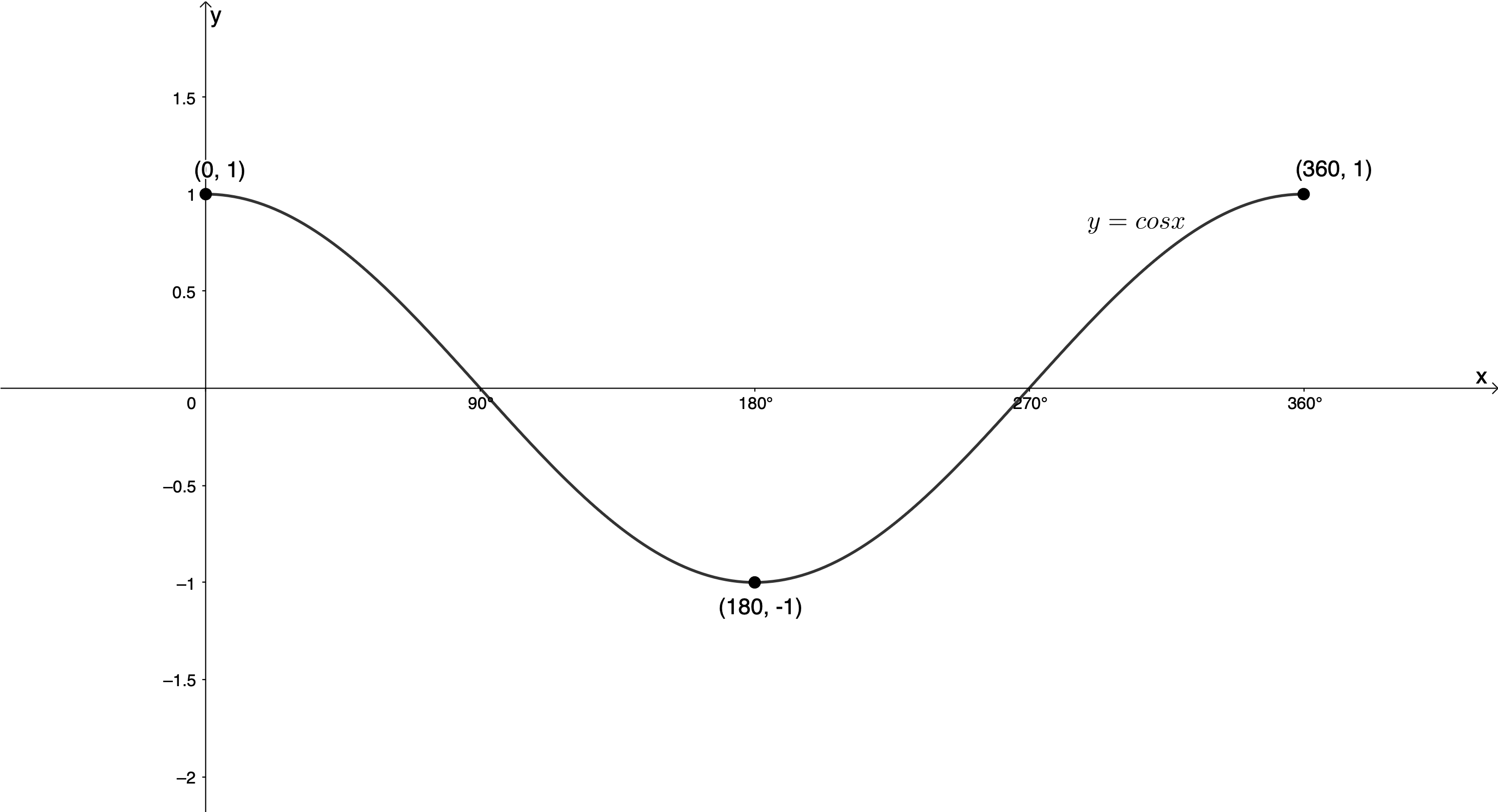
In level 2 we were introduced to the cosine function of the form [latex]\scriptsize y=a\sin \theta +q[/latex]. We discovered that the value of [latex]\scriptsize q[/latex] shifted the graph vertically up and down while the value of [latex]\scriptsize a[/latex] changed the amplitude of the graph.
Take note!
The period of [latex]\scriptsize y=a\cos \theta +q[/latex] is [latex]\scriptsize {{360}^\circ}[/latex].
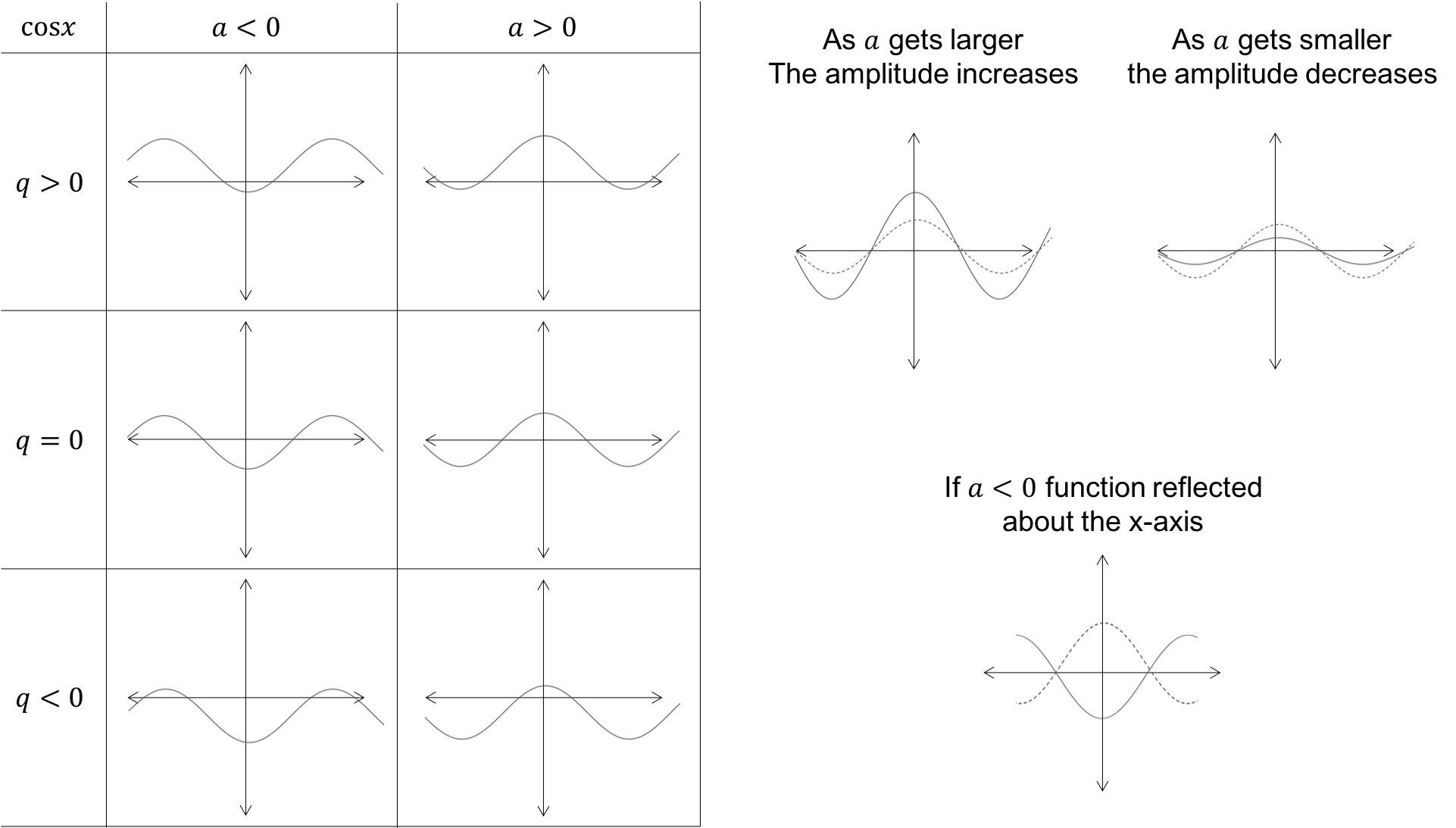
The effect of [latex]\scriptsize q[/latex]:
- if [latex]\scriptsize q \gt 0[/latex], the function is shifted up by [latex]\scriptsize q[/latex] units
- if [latex]\scriptsize q \lt 0[/latex], the function is shifted down by [latex]\scriptsize q[/latex] units.
The effect of [latex]\scriptsize a[/latex]:
- if [latex]\scriptsize a \gt 1[/latex], the amplitude increases to [latex]\scriptsize a[/latex]
- if [latex]\scriptsize 0 \lt a \lt 1[/latex], the amplitude decreases to [latex]\scriptsize a[/latex]
- if [latex]\scriptsize a \lt 0[/latex], the function is reflected about the x-axis
- if [latex]\scriptsize a \lt -1[/latex], the amplitude increases to [latex]\scriptsize a[/latex]
- if [latex]\scriptsize -1 \lt a \lt 0[/latex], the amplitude decreases to [latex]\scriptsize a[/latex].
Note
If you have access to the internet, visit this interactive simulation.
Here you will find a cosine function of the form [latex]\scriptsize y=a\cos x+q[/latex] with sliders to change the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize q[/latex]. Spend some time playing with it to make sure that you understand how changing the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize q[/latex] affect the shape and location of the cosine function of the form [latex]\scriptsize y=a\cos x+q[/latex].
The cosine function of the form [latex]\scriptsize y=\cos kx[/latex]
In Activity 7.1 in unit 7, we saw that the value of [latex]\scriptsize k[/latex] in [latex]\scriptsize y=\sin kx[/latex] affects the period of the function and that we can calculate the period as:
[latex]\scriptsize \text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}[/latex] where [latex]\scriptsize \left| k \right|[/latex] is the absolute value of [latex]\scriptsize k[/latex], in other words the positive value of [latex]\scriptsize k[/latex].
This means that if [latex]\scriptsize k \gt 1[/latex], the period decreases and if [latex]\scriptsize 0 \lt k \lt 1[/latex], the period increases.
The same is true for the cosine function [latex]\scriptsize y=\cos kx[/latex]. The period can be calculated as follows:
[latex]\scriptsize \text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}[/latex] where [latex]\scriptsize \left| k \right|[/latex] is the absolute value of [latex]\scriptsize k[/latex], in other words the positive value of [latex]\scriptsize k[/latex].
This means that if [latex]\scriptsize k \gt 1[/latex], the period decreases and if [latex]\scriptsize 0 \lt k \lt 1[/latex], the period increases.
If [latex]\scriptsize k \lt 0[/latex], it changes the period, but the graph is not reflected about the x-axis. This is because the graph of [latex]\scriptsize y=\cos x[/latex] is symmetrical about the y-axis. Therefore [latex]\scriptsize \cos(-x)=\cos x[/latex] (see Figure 5).
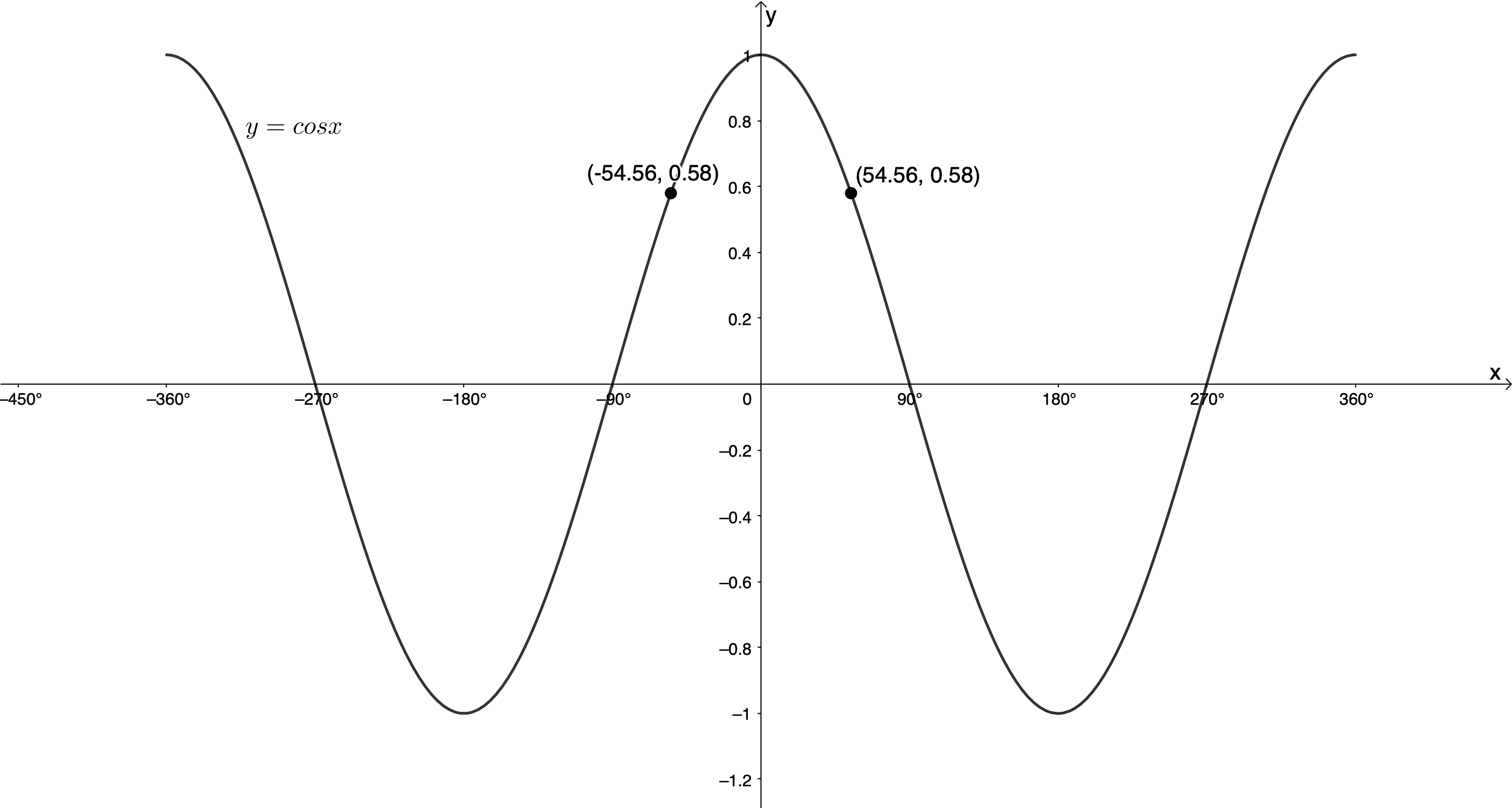
Another way of looking at this is that angles of [latex]\scriptsize -\theta[/latex] lie in the fourth quadrant where the cosine function is positive, as it is in the first quadrant. Therefore, there is no change of sign for the function values.
Note
If you have an internet connection, visit this online simulation to compare the effect values of [latex]\scriptsize k \lt 0[/latex] have on the sine and cosine functions.
Take note!
In [latex]\scriptsize y=\cos kx[/latex] the [latex]\scriptsize \text{period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}[/latex].
[latex]\scriptsize \cos (-x)=\cos (x)[/latex], so the graph is not reflected about the x-axis for [latex]\scriptsize k \lt 0[/latex].
Example 9.1
Given the function [latex]\scriptsize y=\cos \left( {\displaystyle \frac{{2x}}{3}} \right)[/latex] for the interval [latex]\scriptsize {{0}^\circ}\le x\le {{360}^\circ}[/latex], determine the:
- domain and range
- period.
Solutions
- Domain: [latex]\scriptsize \{x|x\in \mathbb{R},\text{ }{{0}^\circ}\le x\le {{360}^\circ}\}[/latex]
Range: [latex]\scriptsize \{y|y\in \mathbb{R},\text{ }-1\le y\le 1\}[/latex] - [latex]\scriptsize k=\displaystyle \frac{2}{3}[/latex]. Therefore, the period of the graph is [latex]\scriptsize \displaystyle \frac{{{{{360}}^\circ}}}{{\left| {\displaystyle \frac{2}{3}} \right|}}=\displaystyle \frac{{3\times {{{360}}^\circ}}}{2}={{540}^\circ}[/latex].
Exercise 9.1
- Determine the periods of the following functions:
- [latex]\scriptsize y=\cos (2x)[/latex]
- [latex]\scriptsize y=\cos \left( {-\displaystyle \frac{3}{5}x} \right)[/latex]
- [latex]\scriptsize y=\cos \left( {-\displaystyle \frac{3}{2}x} \right)[/latex]
- For each function of the form [latex]\scriptsize y=\cos kx[/latex], determine the value of [latex]\scriptsize k[/latex]:
- .
- .
- .
- .
The full solutions are at the end of the unit.
Sketch functions of the form [latex]\scriptsize y=a\cos kx[/latex]
Now that we know that the value of [latex]\scriptsize k[/latex] affects the period of the function [latex]\scriptsize y=\cos kx[/latex], we can combine this with our knowledge of the effects of [latex]\scriptsize a[/latex] and examine functions of the form [latex]\scriptsize y=a\cos kx[/latex].
The effects of [latex]\scriptsize a[/latex] on [latex]\scriptsize y=a\cos kx[/latex] are exactly the same as they were on [latex]\scriptsize y=a\sin x+q[/latex]. Before we learn how to sketch functions of the form [latex]\scriptsize y=a\cos kx[/latex], spend some time playing with this online simulation.
In this simulation you will find a graph of the function [latex]\scriptsize y=a\cos kx+q[/latex] for the interval [latex]\scriptsize -{{360}^\circ}\le x\le {{360}^\circ}[/latex]. Pay particular attention to how the amplitude, period and the values of the turning points and intercepts with the axes change as you change the values of [latex]\scriptsize a[/latex], [latex]\scriptsize k[/latex] and [latex]\scriptsize q[/latex].
The best way to sketch functions of the form [latex]\scriptsize y=a\cos kx[/latex] is to transform the basic function of [latex]\scriptsize y=\cos x[/latex] depending on the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex]. To do this, you need to know the set of ‘anchor points’ of [latex]\scriptsize y=\cos x[/latex], as transformation of these points will help you to sketch functions of the form [latex]\scriptsize y=a\cos kx[/latex].
Take note!
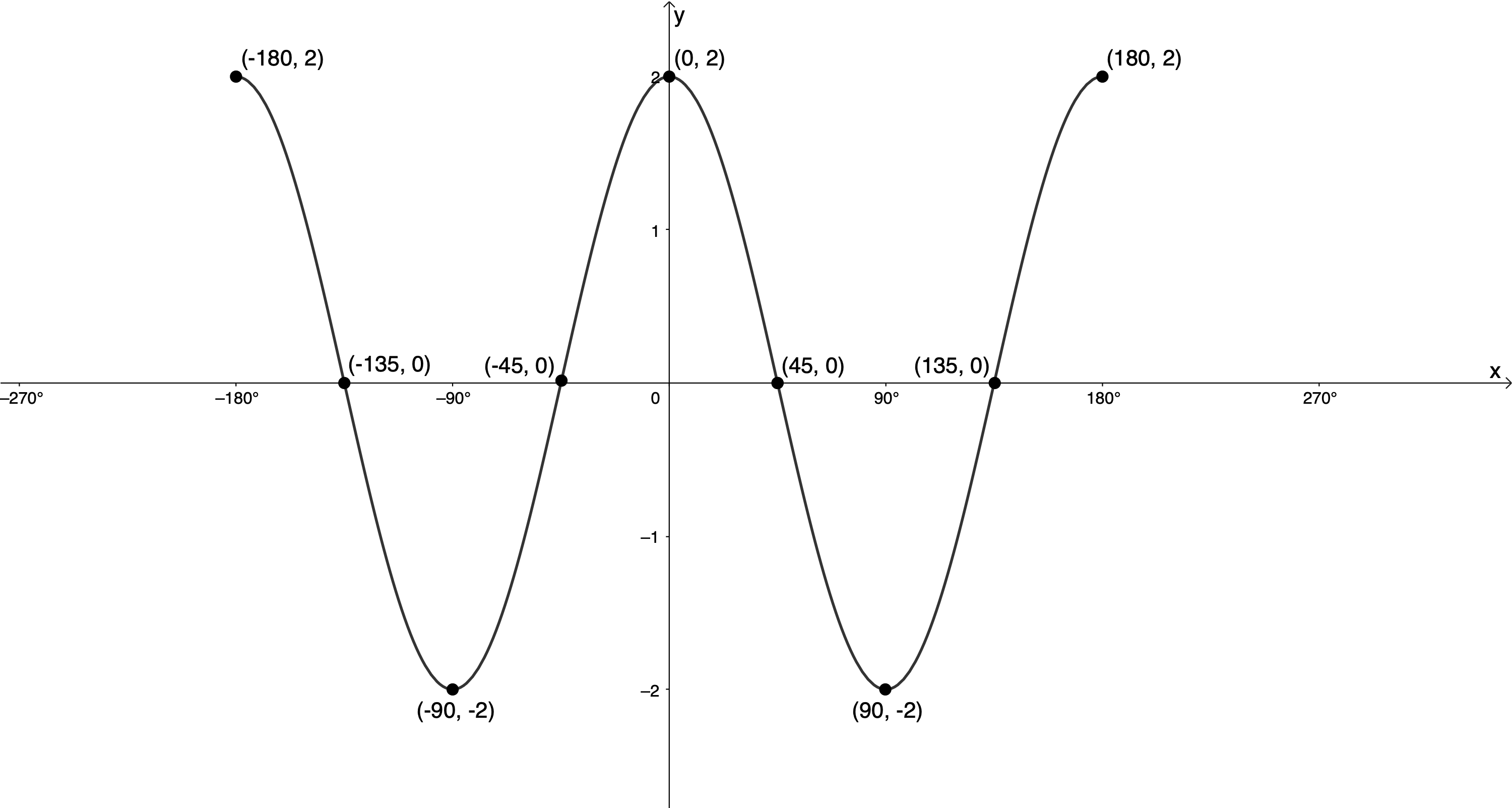
The ‘anchor points’ for [latex]\scriptsize y=\cos x[/latex] are illustrated in Figure 6 for the interval [latex]\scriptsize -{{360}^\circ}\le x\le {{360}^\circ}[/latex].
Example 9.2
Sketch the function [latex]\scriptsize y=2\cos 2x[/latex] for the interval [latex]\scriptsize -{{180}^\circ}\le x\le {{180}^\circ}[/latex].
Solution
The function is of the form [latex]\scriptsize y=a\cos kx[/latex], with[latex]\scriptsize a=2[/latex] and [latex]\scriptsize k=2[/latex].
Because [latex]\scriptsize k=2[/latex], we know that the period of the function will be [latex]\scriptsize \displaystyle \frac{{{{{360}}^\circ}}}{{\left| 2 \right|}}={{180}^\circ}[/latex]. We need to transform one period of ‘anchor points’ as follows:
| [latex]\scriptsize \cos x[/latex] | [latex]\scriptsize ({{0}^\circ},1)[/latex] | [latex]\scriptsize ({{90}^\circ},0)[/latex] | [latex]\scriptsize ({{180}^\circ},-1)[/latex] | [latex]\scriptsize ({{270}^\circ},0)[/latex] | [latex]\scriptsize ({{360}^\circ},1)[/latex] |
| [latex]\scriptsize \cos 2x[/latex] | [latex]\scriptsize ({{0}^\circ},1)[/latex] | [latex]\scriptsize ({{45}^\circ},0)[/latex] | [latex]\scriptsize ({{90}^\circ},-1)[/latex] | [latex]\scriptsize ({{135}^\circ},0)[/latex] | [latex]\scriptsize ({{180}^\circ},1)[/latex] |
Because the period has been halved, the value of each of the x-coordinates is also halved. We can see that the function will start at[latex]\scriptsize 1[/latex], which is its maximum turning point [latex]\scriptsize ({{0}^\circ},1)[/latex], fall to zero , fall to its minimum turning point [latex]\scriptsize ({{90}^\circ},-1)[/latex], rise back to zero and rise back to its maximum turning point [latex]\scriptsize ({{180}^\circ},1)[/latex] in [latex]\scriptsize {{180}^\circ}[/latex], the new period.
Because [latex]\scriptsize a=2[/latex], we know that each function value (or y-value) is going to be multiplied by [latex]\scriptsize 2[/latex] thereby making the amplitude of the function [latex]\scriptsize 2[/latex]. We need to further transform one period of ‘anchor points’ as follows:
| [latex]\scriptsize \cos x[/latex] | [latex]\scriptsize ({{0}^\circ},1)[/latex] | [latex]\scriptsize ({{90}^\circ},0)[/latex] | [latex]\scriptsize ({{180}^\circ},-1)[/latex] | [latex]\scriptsize ({{270}^\circ},0)[/latex] | [latex]\scriptsize ({{360}^\circ},1)[/latex] |
| [latex]\scriptsize \cos 2x[/latex] | [latex]\scriptsize ({{0}^\circ},1)[/latex] | [latex]\scriptsize ({{45}^\circ},0)[/latex] | [latex]\scriptsize ({{90}^\circ},-1)[/latex] | [latex]\scriptsize ({{135}^\circ},0)[/latex] | [latex]\scriptsize ({{180}^\circ},1)[/latex] |
| [latex]\scriptsize 2\cos 2x[/latex] | [latex]\scriptsize ({{0}^\circ},2)[/latex] | [latex]\scriptsize ({{45}^\circ},0)[/latex] | [latex]\scriptsize ({{90}^\circ},-2)[/latex] | [latex]\scriptsize ({{135}^\circ},0)[/latex] | [latex]\scriptsize ({{180}^\circ},2)[/latex] |
We can see that the function will start at [latex]\scriptsize 2[/latex], which is its new maximum turning point [latex]\scriptsize ({{0}^\circ},2)[/latex], fall to zero, fall to its new minimum turning point [latex]\scriptsize ({{90}^\circ},-2)[/latex], rise back to zero and rise back to its new maximum turning point [latex]\scriptsize ({{180}^\circ},2)[/latex] in [latex]\scriptsize {{180}^\circ}[/latex], the new period.
We can now plot our transformed ‘anchor points’ and draw the graph. We first draw it for the interval [latex]\scriptsize {{0}^\circ}\le x\le {{180}^\circ}[/latex] and then continue the pattern for the full interval of [latex]\scriptsize -{{180}^\circ}\le x\le {{180}^\circ}[/latex].
Example 9.3
Given the function [latex]\scriptsize f(x)=3\cos \left( {-\displaystyle \frac{1}{2}x} \right)[/latex]:
- Sketch the graph of [latex]\scriptsize f(x)[/latex] for the interval [latex]\scriptsize -{{360}^\circ}\le x\le {{360}^\circ}[/latex].
- State the domain and range of [latex]\scriptsize f(x)[/latex].
- List the turning points of [latex]\scriptsize f(x)[/latex].
- What is the amplitude of [latex]\scriptsize f(x)[/latex]?
- What is the period of [latex]\scriptsize f(x)[/latex]?
Solutions
- The function is of the form [latex]\scriptsize y=a\cos kx[/latex] with [latex]\scriptsize a=3[/latex] and [latex]\scriptsize k=-\displaystyle \frac{1}{2}[/latex].
.
Because [latex]\scriptsize k=-\displaystyle \frac{1}{2}[/latex], we know that the period of the function will be [latex]\scriptsize \displaystyle \frac{{{{{360}}^\circ}}}{{\left| {-\displaystyle \frac{1}{2}} \right|}}=\displaystyle \frac{{{{{360}}^\circ}}}{{\displaystyle \frac{1}{2}}}={{720}^\circ}\text{ }[/latex].
.
We need to transform one period of ‘anchor points’ as follows:[latex]\scriptsize \cos x[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{90}^\circ},0)[/latex] [latex]\scriptsize ({{180}^\circ},-1)[/latex] [latex]\scriptsize ({{270}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},1)[/latex] [latex]\scriptsize \cos \left( {-\displaystyle \frac{1}{2}x} \right)[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{180}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},-1)[/latex] [latex]\scriptsize ({{540}^\circ},0)[/latex] [latex]\scriptsize ({{720}^\circ},1)[/latex] .
Because the period has been doubled, the value of each of the x-coordinates is also doubled. We can see that the function will start at [latex]\scriptsize 1[/latex], which is its maximum turning point [latex]\scriptsize ({{0}^\circ},1)[/latex], fall to zero , fall to its minimum turning point [latex]\scriptsize ({{360}^\circ},-1)[/latex], rise back to zero and rise back to its maximum turning point [latex]\scriptsize ({{720}^\circ},1)[/latex] in [latex]\scriptsize {{720}^\circ}[/latex], the new period.
.
Because [latex]\scriptsize a=3[/latex], we know that each function value (or y-value) is going to be multiplied by [latex]\scriptsize 3[/latex] thereby making the amplitude of the function [latex]\scriptsize 3[/latex]. We need to further transform one period of ‘anchor points’ as follows:[latex]\scriptsize \cos x[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{90}^\circ},0)[/latex] [latex]\scriptsize ({{180}^\circ},-1)[/latex] [latex]\scriptsize ({{270}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},1)[/latex] [latex]\scriptsize \cos \left( {-\displaystyle \frac{1}{2}x} \right)[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{180}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},-1)[/latex] [latex]\scriptsize ({{540}^\circ},0)[/latex] [latex]\scriptsize ({{720}^\circ},1)[/latex] [latex]\scriptsize 3\cos \left( {-\displaystyle \frac{1}{2}x} \right)[/latex] [latex]\scriptsize ({{0}^\circ},3)[/latex] [latex]\scriptsize ({{180}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},-3)[/latex] [latex]\scriptsize ({{540}^\circ},0)[/latex] [latex]\scriptsize ({{720}^\circ},3)[/latex] .
We can see that the function will start at , which is its new maximum turning point [latex]\scriptsize ({{0}^\circ},3)[/latex], fall to zero , fall to its new minimum turning point [latex]\scriptsize ({{360}^\circ},-3)[/latex], rise back to zero and rise back to its new maximum turning point [latex]\scriptsize ({{720}^\circ},3)[/latex] in [latex]\scriptsize {{720}^\circ}[/latex], the new period.
.
We can now plot our transformed ‘anchor points’ and draw the graph for the interval [latex]\scriptsize -{{360}^\circ}\le x\le {{360}^\circ}[/latex].
.
- Domain: [latex]\scriptsize \{x|x\in \mathbb{R},\text{ }-{{360}^\circ}\le x\le {{360}^\circ}\}[/latex]
Range[latex]\scriptsize \{f(x)|f(x)\in \mathbb{R},\text{ }-3\le f(x)\le 3\}[/latex] - Turning points: [latex]\scriptsize (-{{360}^\circ},3)[/latex], [latex]\scriptsize ({{0}^\circ},3)[/latex] and [latex]\scriptsize ({{360}^\circ},-3)[/latex]
- Amplitude is [latex]\scriptsize 3[/latex]
- Period is [latex]\scriptsize {{720}^\circ}[/latex]
Exercise 9.2
Sketch the following functions for the indicated intervals:
- [latex]\scriptsize y=-2\cos \displaystyle \frac{\theta }{2}[/latex] for [latex]\scriptsize -{{360}^\circ}\le \theta \le {{360}^\circ}[/latex]
- [latex]\scriptsize \displaystyle y=\cos \left( {-\displaystyle \frac{{3x}}{2}} \right)[/latex] for [latex]\scriptsize -{{180}^\circ}\le x\le {{180}^\circ}[/latex]
- [latex]\scriptsize y=\displaystyle \frac{1}{2}\cos 3\theta[/latex] for [latex]\scriptsize -{{180}^\circ}\le \theta \le {{180}^\circ}[/latex]
The full solutions are at the end of the unit.
Find the equation of a cosine function of the form [latex]\scriptsize y=a\cos kx[/latex]
By examining the amplitude and period of a graph of the form [latex]\scriptsize y=a\cos kx[/latex], we can determine the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex].
Example 9.4
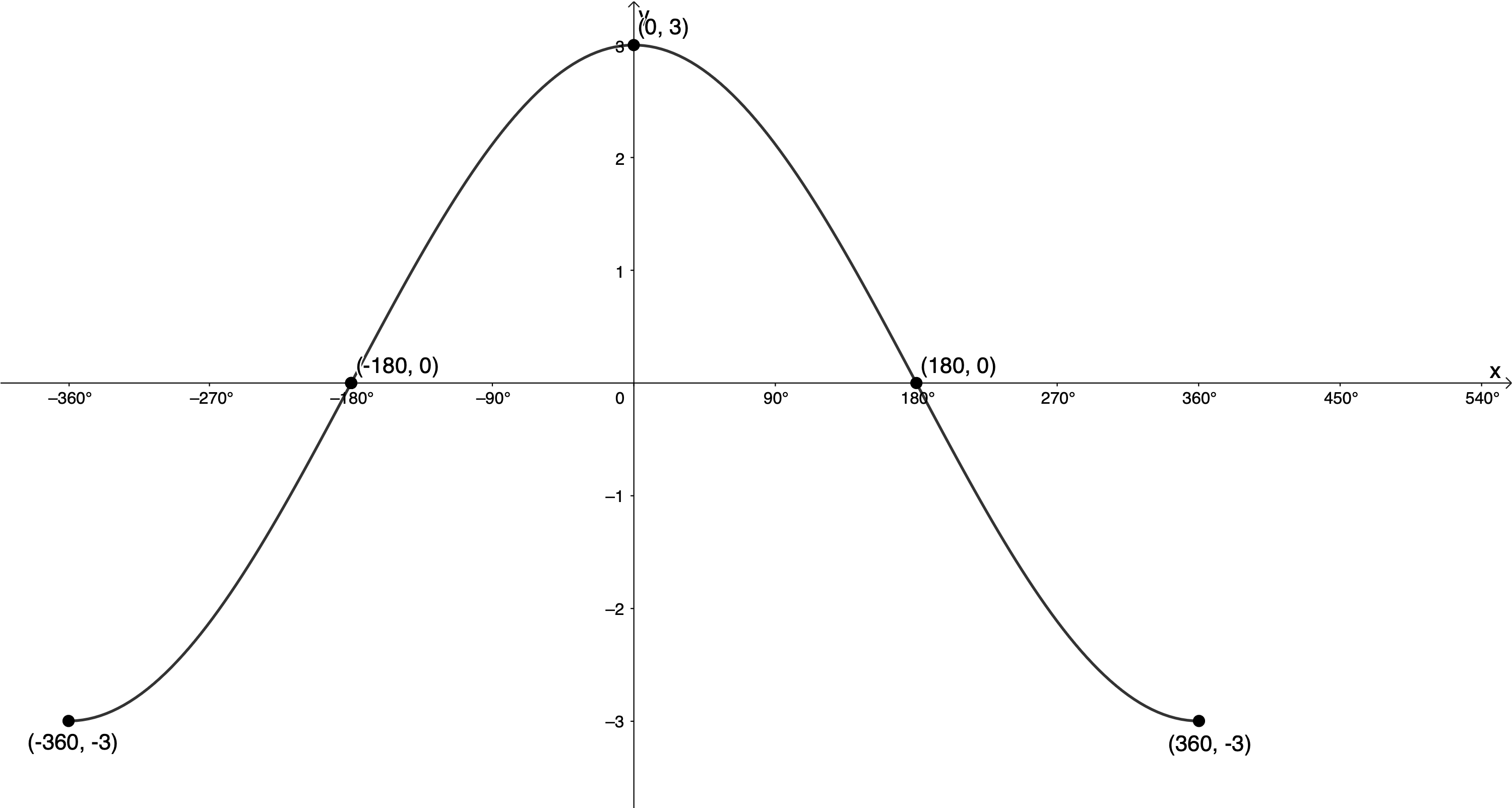
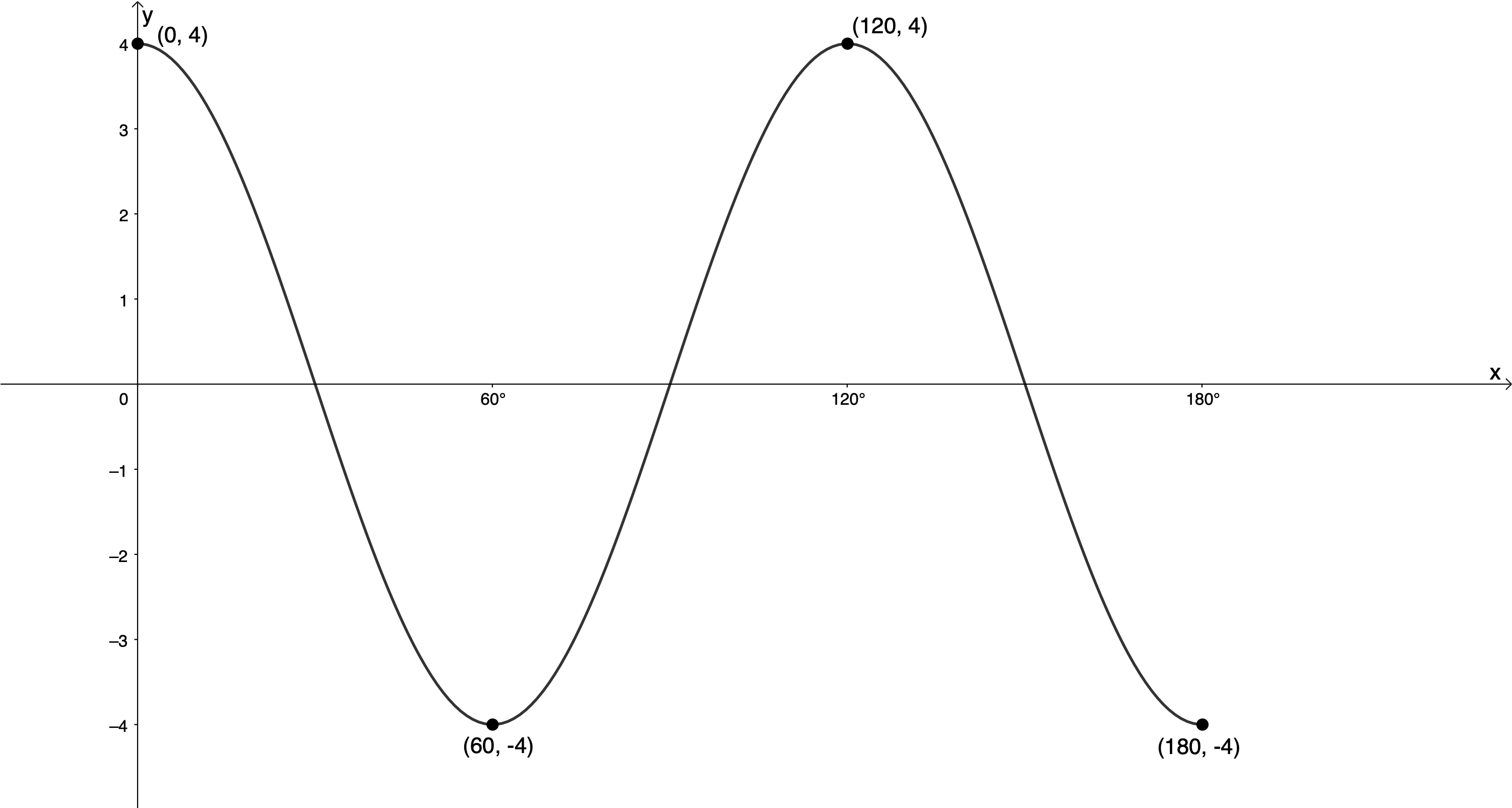
Given the following graph of the form [latex]\scriptsize y=a\cos kx[/latex], determine the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex]:
Solution
From the graph we can see that the amplitude is [latex]\scriptsize 4[/latex]. We can also see that the graph is not reflected about the x-axis. At zero, it is at its maximum turning point in the same way as the graph of [latex]\scriptsize y=\cos x[/latex]. Therefore, [latex]\scriptsize a=4[/latex] and [latex]\scriptsize y=4\cos kx[/latex].
The period is [latex]\scriptsize {{120}^\circ}[/latex].
[latex]\scriptsize \begin{align*}\text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\{{120}^\circ}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\\therefore \left| k \right|=3\text{ }\end{align*}[/latex]
[latex]\scriptsize y=4\cos 3x[/latex]
Example 9.5
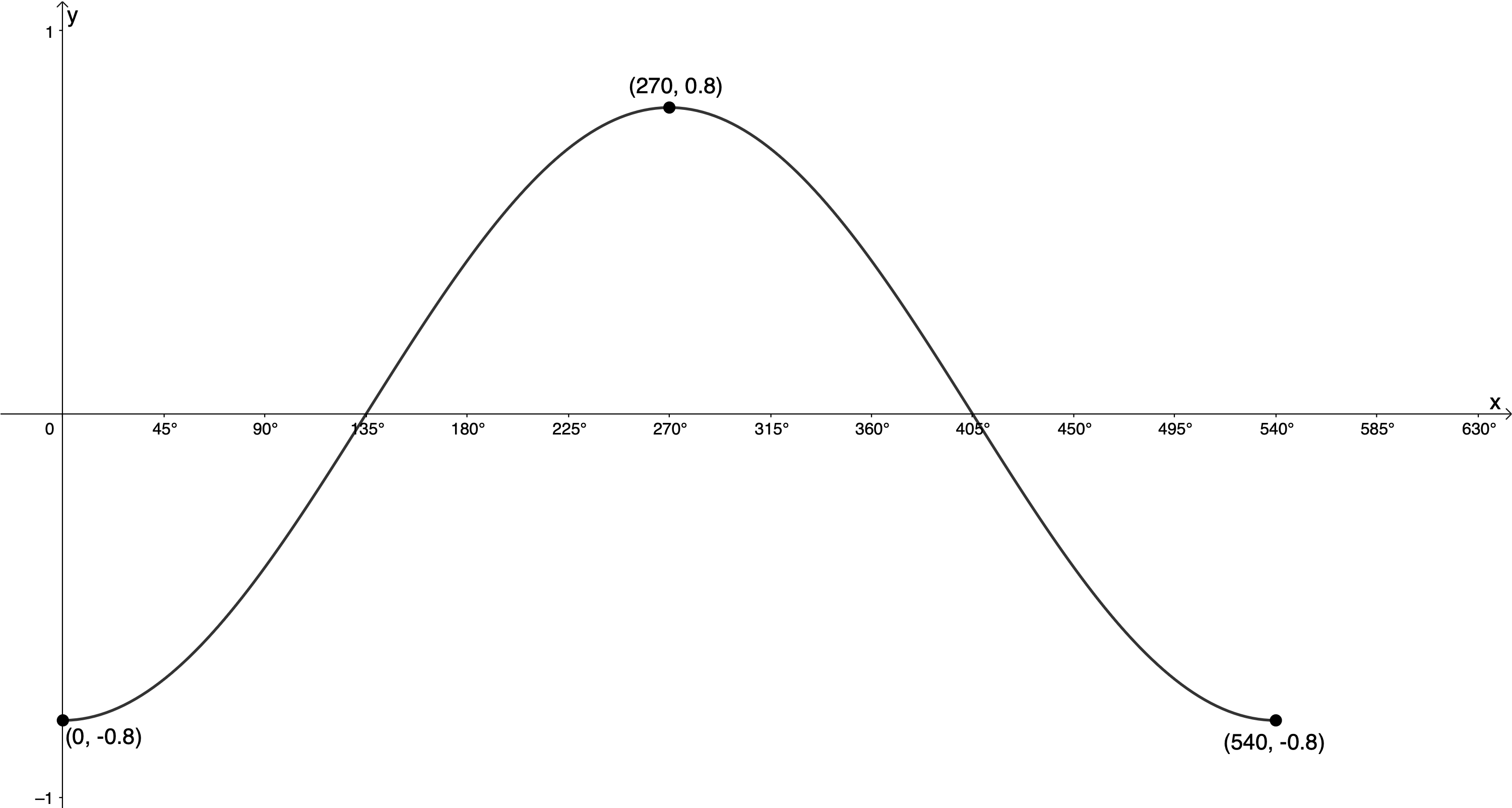
Given the following graph of the form [latex]\scriptsize y=a\cos kx[/latex], determine the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex]:
Solution
From the graph we can see that the amplitude is [latex]\scriptsize 0.8=\displaystyle \frac{4}{5}[/latex]. We can also see that the graph is reflected about the x-axis. At zero, it is at its minimum turning point unlike the graph of [latex]\scriptsize \displaystyle y=\cos x[/latex] which is at its maximum turning point. Therefore, [latex]\scriptsize a=-\displaystyle \frac{4}{5}[/latex] and [latex]\scriptsize y=-\displaystyle \frac{4}{5}\cos kx[/latex].
[latex]\scriptsize \begin{align*}\text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\{{540}^\circ}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\\therefore \left| k \right|=\displaystyle \frac{{{{{360}}^\circ}}}{{{{{540}}^\circ}}}=\displaystyle \frac{2}{3}\text{ }\end{align*}[/latex]
[latex]\scriptsize y=-\displaystyle \frac{4}{5}\cos \left( {\displaystyle \frac{2}{3}x} \right)[/latex]
Exercise 9.3
Given the graph of the form [latex]\scriptsize y=a\cos kx[/latex]:
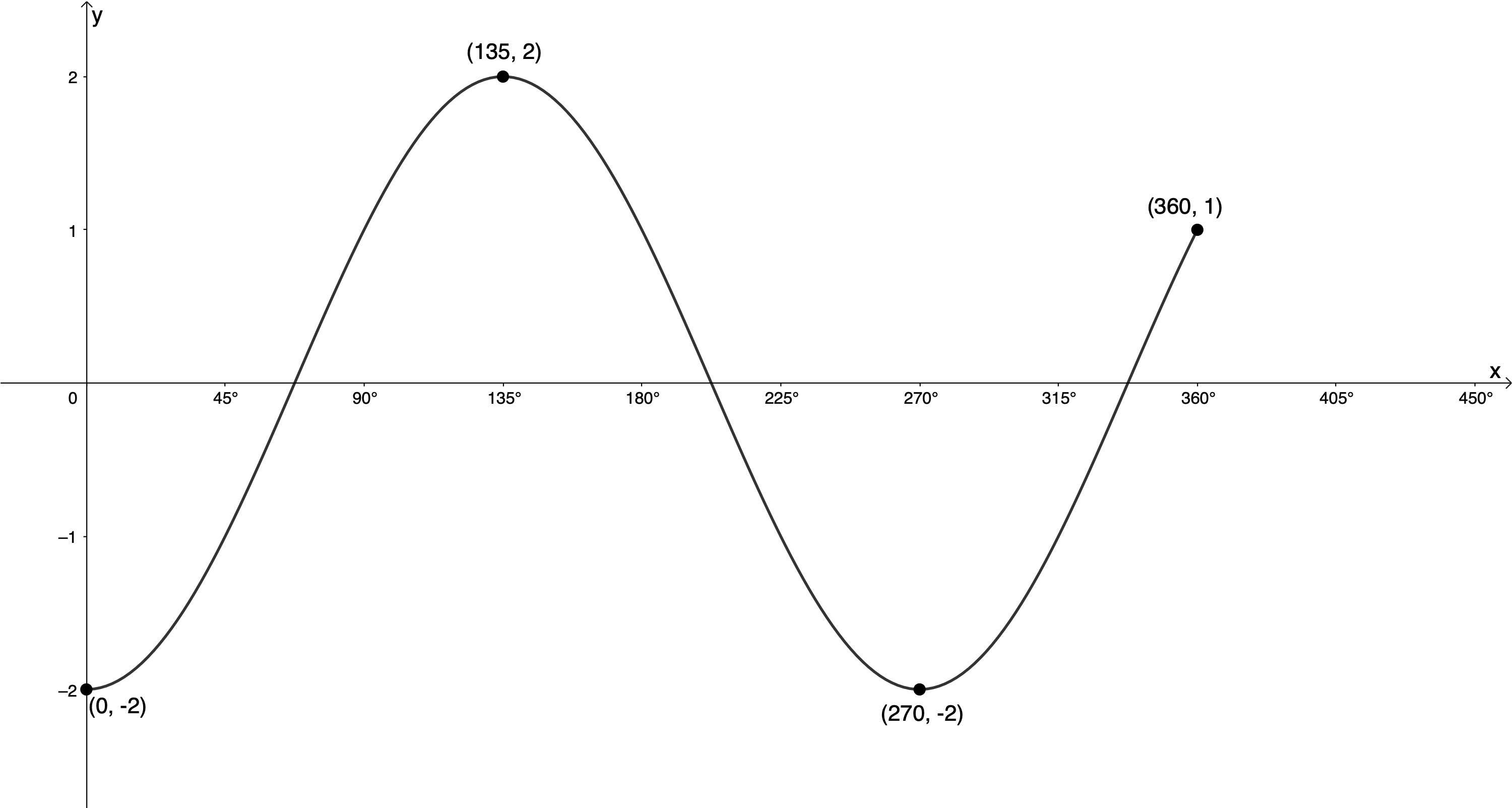
- Determine the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex].
- State the domain and range of the function.
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- The effects of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex] on the cosine graph of the form [latex]\scriptsize y=a\cos k\theta[/latex].
- How to sketch functions of the form [latex]\scriptsize y=a\cos k\theta[/latex].
- How to find the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex] from a given cosine graph of the form [latex]\scriptsize y=a\cos k\theta[/latex].
Unit 9: Assessment
Suggested time to complete: 45 minutes
- Sketch the following functions for the given intervals:
- [latex]\scriptsize 3y=\cos \left( {\displaystyle \frac{1}{2}x} \right)[/latex] for [latex]\scriptsize -{{720}^\circ}\le x\le {{360}^\circ}[/latex]
- [latex]\scriptsize g(x)=-3\cos 2x[/latex] for [latex]\scriptsize {{0}^\circ}\le x\le {{270}^\circ}[/latex]
- From the graph below of the form [latex]\scriptsize y=a\cos kx[/latex], determine the values of [latex]\scriptsize a[/latex] and [latex]\scriptsize k[/latex]:
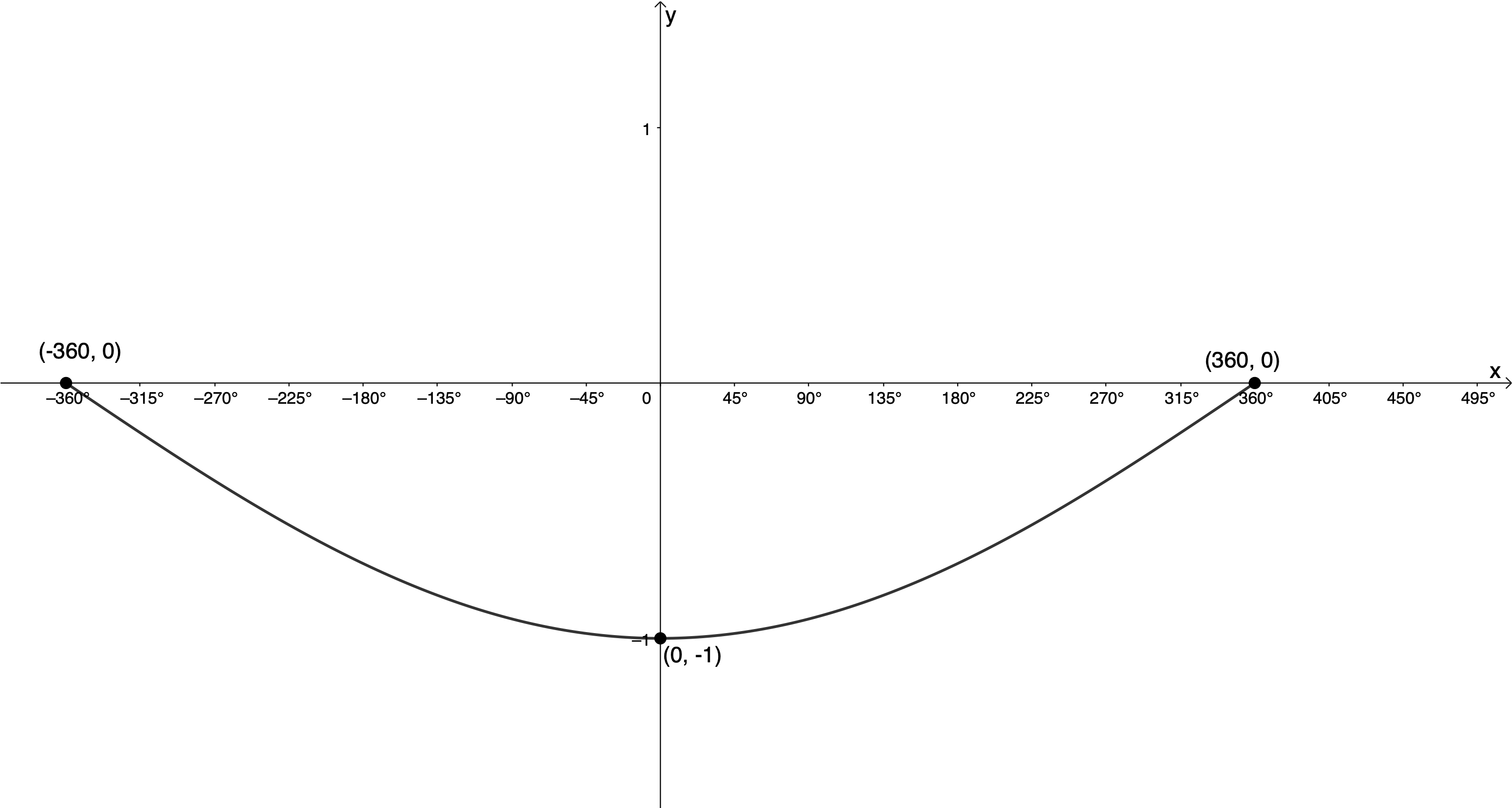
The full solutions are at the end of the unit.
Unit 9: Solutions
Exercise 9.1
- .
- [latex]\scriptsize y=\cos (2x)[/latex]
[latex]\scriptsize k=2[/latex]
[latex]\scriptsize \text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| 2 \right|}}=\displaystyle \frac{{{{{360}}^\circ}}}{2}={{180}^\circ}\text{ }[/latex] - [latex]\scriptsize y=\cos \left( {-\displaystyle \frac{3}{5}x} \right)[/latex]
[latex]\scriptsize k=-\displaystyle \frac{3}{5}[/latex]
[latex]\scriptsize \text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| {-\displaystyle \frac{3}{5}} \right|}}=\displaystyle \frac{{{{{360}}^\circ}}}{{\displaystyle \frac{3}{5}}}=\displaystyle \frac{{5\times {{{360}}^\circ}}}{3}={{600}^\circ}[/latex] - [latex]\scriptsize y=\cos \left( {-\displaystyle \frac{3}{2}x} \right)[/latex]
[latex]\scriptsize k=-\displaystyle \frac{3}{2}[/latex]
[latex]\scriptsize \text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| {-\displaystyle \frac{3}{2}} \right|}}=\displaystyle \frac{{2\times {{{360}}^\circ}}}{3}={{240}^\circ}[/latex]
- [latex]\scriptsize y=\cos (2x)[/latex]
- .
- The period of the graph is [latex]\scriptsize {{720}^\circ}[/latex].
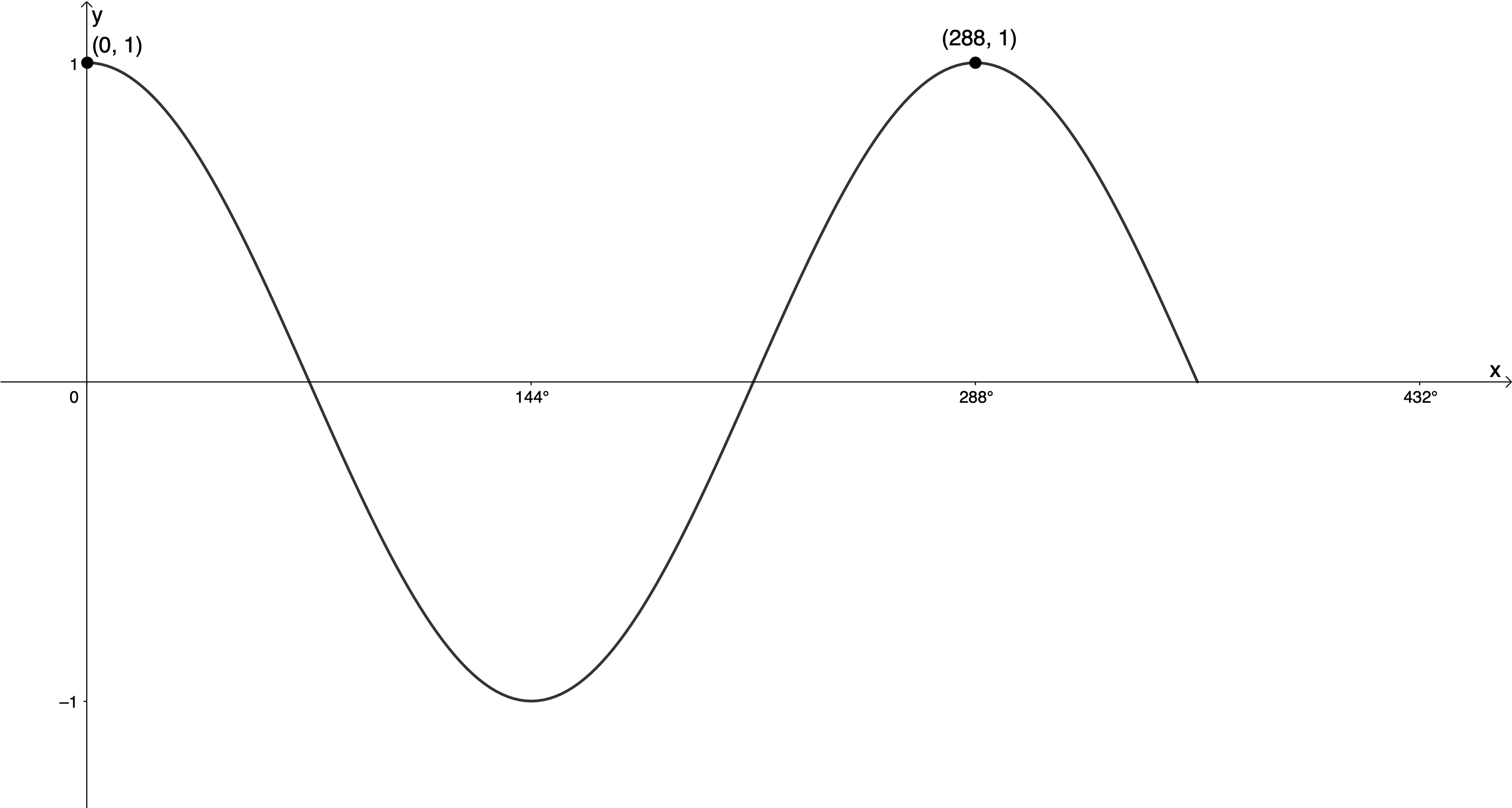
[latex]\scriptsize \begin{align*}\text{Period} & =\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\{{720}^\circ} & =\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\\therefore \left| k \right| & =\displaystyle \frac{{{{{360}}^\circ}}}{{{{{720}}^\circ}}}\\\therefore \left| k \right| & =\displaystyle \frac{1}{2}\end{align*}[/latex] - The period of the graph is [latex]\scriptsize {{288}^\circ}[/latex].
[latex]\scriptsize \displaystyle \begin{align*}\text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\{{288}^\circ}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\\therefore \left| k \right|=\displaystyle \frac{{{{{360}}^\circ}}}{{{{{288}}^\circ}}}=\displaystyle \frac{5}{4}\text{ }\end{align*}[/latex] - The period of the graph is .
[latex]\scriptsize \begin{align*}\text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\{{120}^\circ}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\\therefore \left| k \right|=\displaystyle \frac{{{{{360}}^\circ}}}{{{{{120}}^\circ}}}=3\text{ }\end{align*}[/latex]
- The period of the graph is [latex]\scriptsize {{720}^\circ}[/latex].
Exercise 9.2
- [latex]\scriptsize y=-2\cos \displaystyle \frac{\theta }{2}[/latex] for [latex]\scriptsize -{{360}^\circ}\le \theta \le {{360}^\circ}[/latex]
[latex]\scriptsize k=\displaystyle \frac{1}{2}[/latex]
[latex]\scriptsize \text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| {\displaystyle \frac{1}{2}} \right|}}={{720}^\circ}[/latex]
[latex]\scriptsize a=-2[/latex]. Amplitude is [latex]\scriptsize 2[/latex] and graph is reflected about the x-axis.[latex]\scriptsize \cos \theta[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{90}^\circ},0)[/latex] [latex]\scriptsize ({{180}^\circ},-1)[/latex] [latex]\scriptsize ({{270}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},1)[/latex] [latex]\scriptsize -2\cos \left( {\displaystyle \frac{\theta }{2}} \right)[/latex] [latex]\scriptsize ({{0}^\circ},-2)[/latex] [latex]\scriptsize ({{180}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},2)[/latex] [latex]\scriptsize ({{540}^\circ},0)[/latex] [latex]\scriptsize ({{720}^\circ},-2)[/latex] 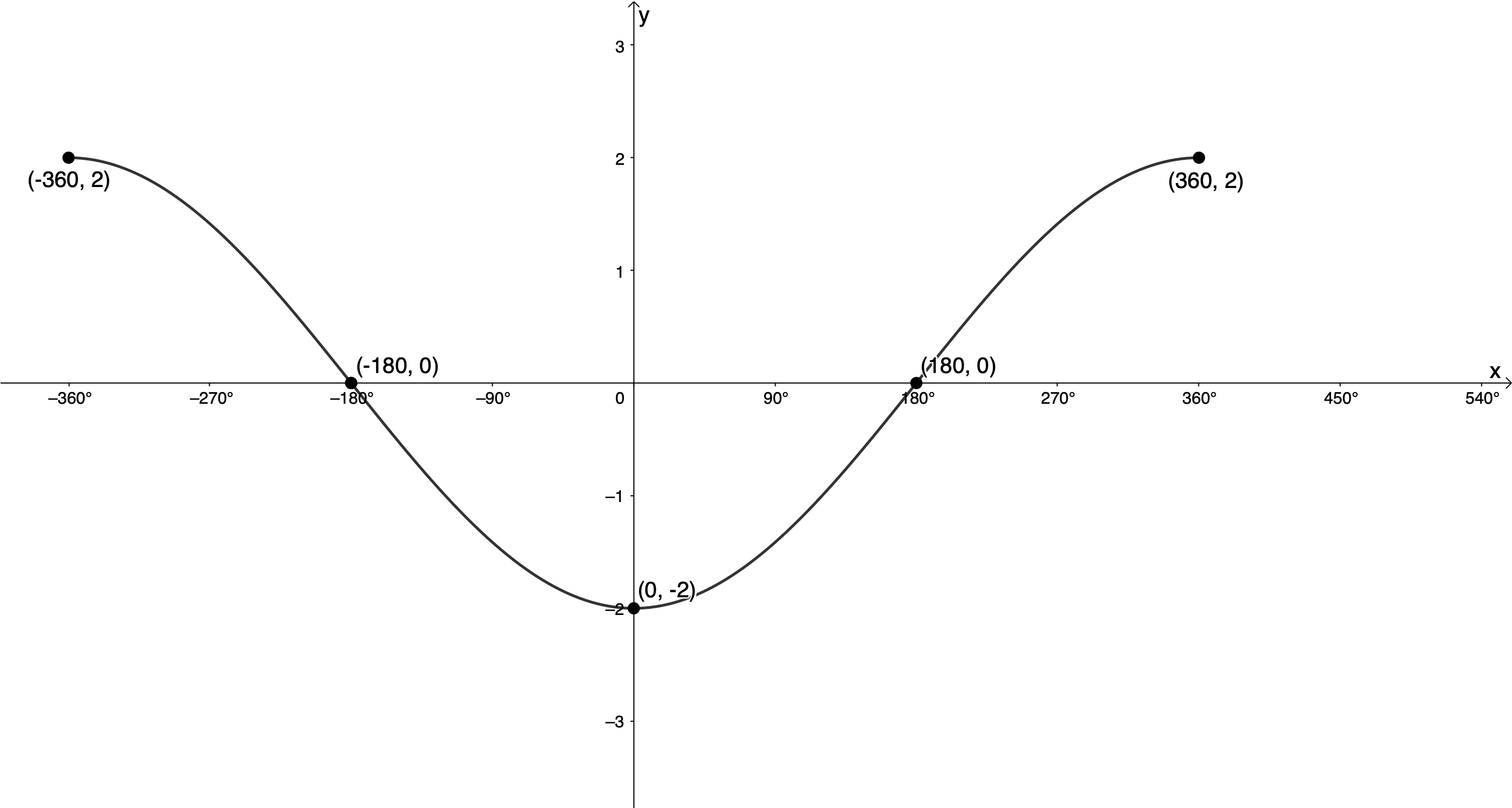
- [latex]\scriptsize y=\cos \left( {-\displaystyle \frac{{3x}}{2}} \right)[/latex] for [latex]\scriptsize -{{180}^\circ}\le x\le {{180}^\circ}[/latex]
[latex]\scriptsize k=-\displaystyle \frac{3}{2}[/latex]
[latex]\scriptsize \text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| {-\displaystyle \frac{3}{2}} \right|}}=\displaystyle \frac{{{{{360}}^\circ}}}{{\displaystyle \frac{3}{2}}}={{240}^\circ}[/latex]
[latex]\scriptsize a=1[/latex]. Amplitude is [latex]\scriptsize 1[/latex] and the graph is not reflected about the x-axis.[latex]\scriptsize \cos x[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{90}^\circ},0)[/latex] [latex]\scriptsize ({{180}^\circ},-1)[/latex] [latex]\scriptsize ({{270}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},1)[/latex] [latex]\scriptsize \cos \left( {-\displaystyle \frac{{3x}}{2}} \right)[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{60}^\circ},0)[/latex] [latex]\scriptsize ({{120}^\circ},-1)[/latex] [latex]\scriptsize ({{180}^\circ},0)[/latex] [latex]\scriptsize ({{240}^\circ},1)[/latex] 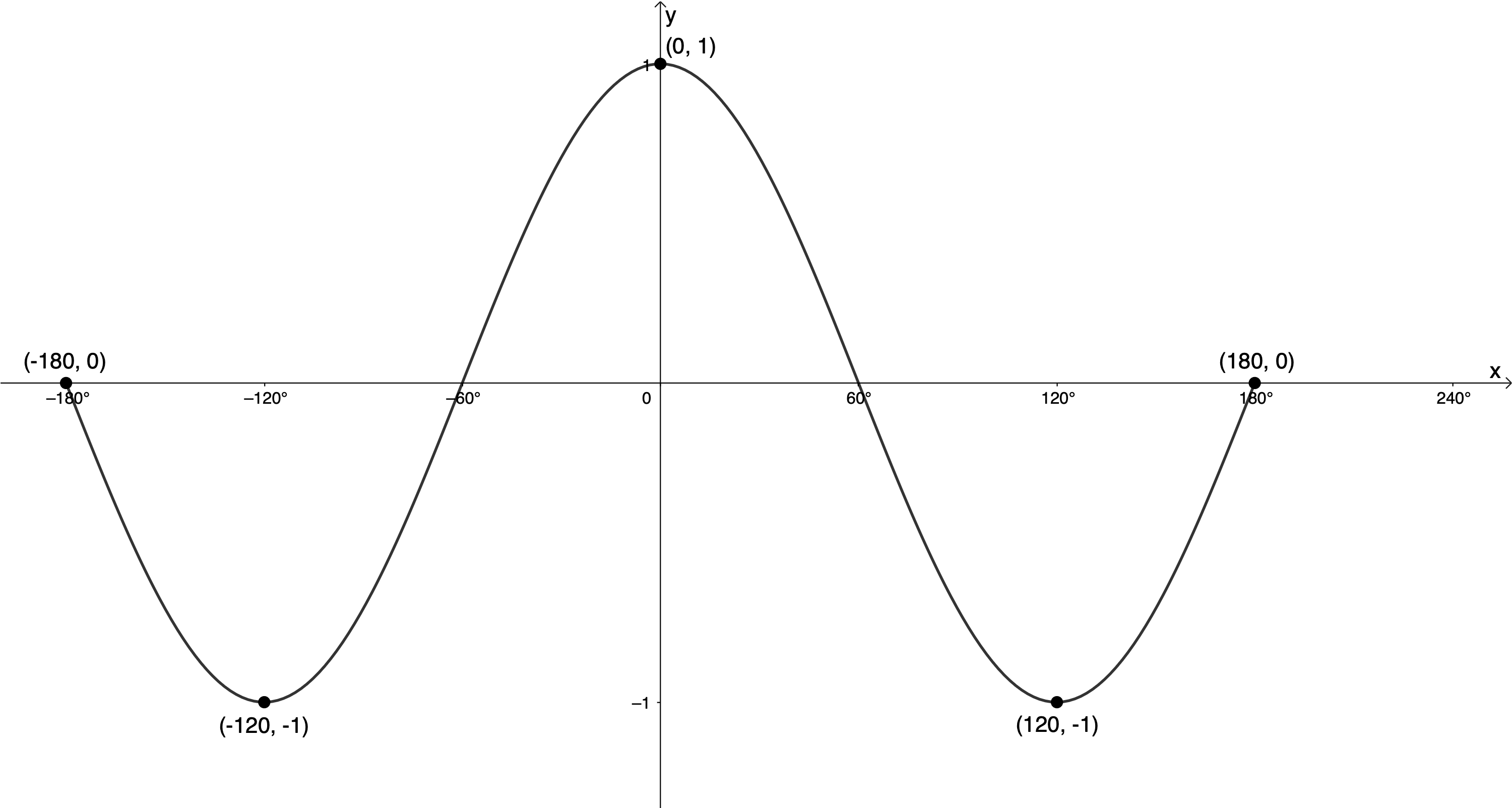
- [latex]\scriptsize y=\displaystyle \frac{1}{2}\cos 3\theta[/latex] for [latex]\scriptsize -{{180}^\circ}\le x\le {{180}^\circ}[/latex]
[latex]\scriptsize k=3[/latex]
[latex]\scriptsize \text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| 3 \right|}}={{120}^\circ}[/latex]
[latex]\scriptsize a=\displaystyle \frac{1}{2}[/latex]. Amplitude is [latex]\scriptsize \displaystyle \frac{1}{2}[/latex] and graph is not reflected about the x-axis.[latex]\scriptsize \cos \theta[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{90}^\circ},0)[/latex] [latex]\scriptsize ({{180}^\circ},-1)[/latex] [latex]\scriptsize ({{270}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},1)[/latex] [latex]\scriptsize \displaystyle \frac{1}{2}\cos \left( {3\theta } \right)[/latex] [latex]\scriptsize ({{0}^\circ},\displaystyle \frac{1}{2})[/latex] [latex]\scriptsize ({{30}^\circ},0)[/latex] [latex]\scriptsize ({{60}^\circ},-\displaystyle \frac{1}{2})[/latex] [latex]\scriptsize ({{90}^\circ},0)[/latex] [latex]\scriptsize ({{120}^\circ},\displaystyle \frac{1}{2})[/latex] 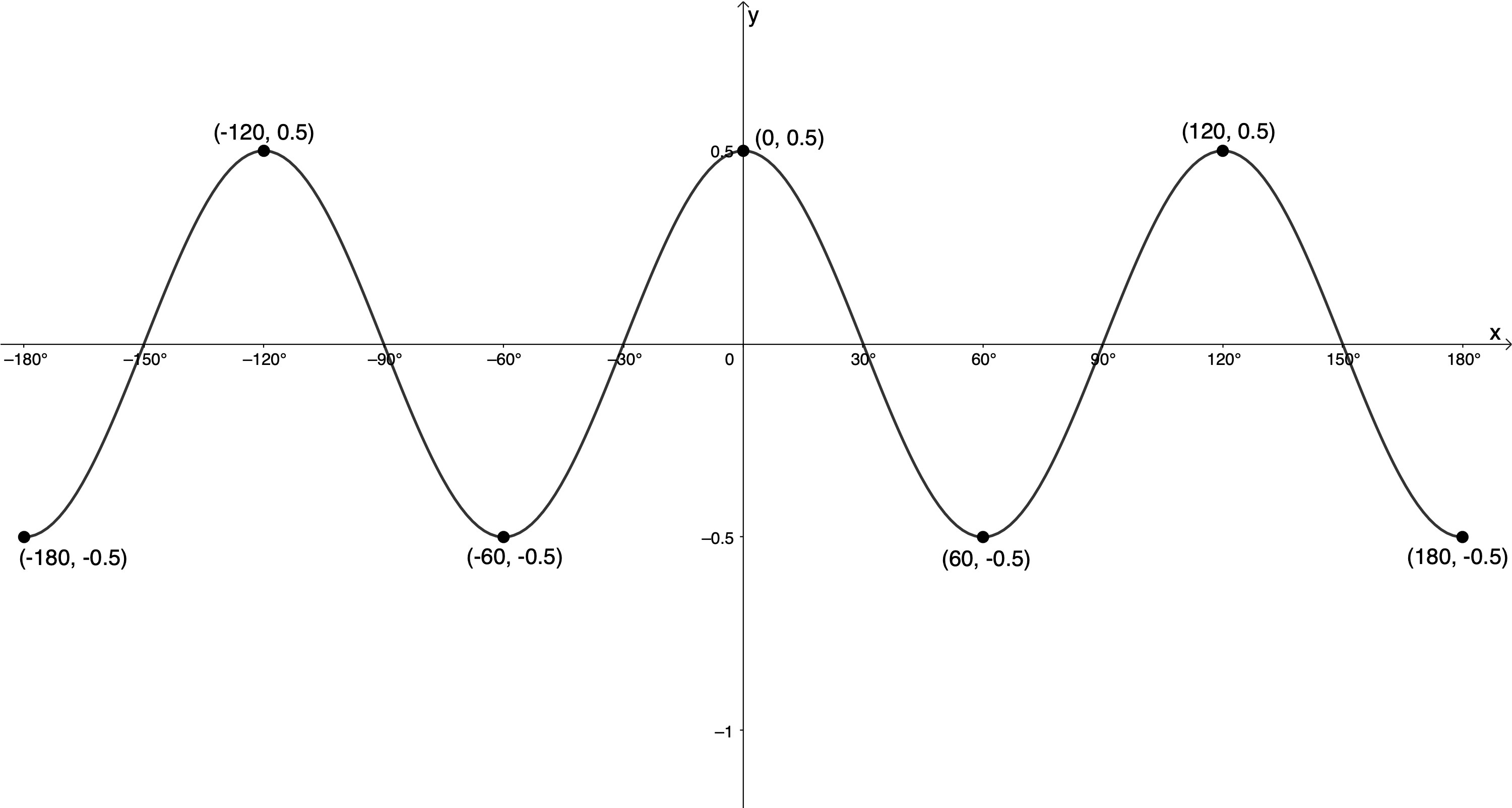
Exercise 9.3
- The amplitude of the function is [latex]\scriptsize 2[/latex]and graph is reflected about the x-axis. Therefore, [latex]\scriptsize a=-2[/latex] and [latex]\scriptsize y=-2\cos kx[/latex].
The period is [latex]\scriptsize {{270}^\circ}[/latex]. Therefore [latex]\scriptsize k=\displaystyle \frac{{{{{360}}^\circ}}}{{{{{270}}^\circ}}}=\displaystyle \frac{4}{3}[/latex].
[latex]\scriptsize y=-2\cos \left( {\displaystyle \frac{4}{3}x} \right)[/latex] - Domain: [latex]\scriptsize \{x|x\in \mathbb{R},{{0}^\circ}\le x\le {{360}^\circ}\}\text{ }[/latex]
Range: [latex]\scriptsize \{y|y\in \mathbb{R},\text{ }-2\le x\le 2\}[/latex]
Unit 9: Assessment
- .
- [latex]\scriptsize 3y=\cos \left( {\displaystyle \frac{1}{2}x} \right)[/latex] for [latex]\scriptsize -{{720}^\circ}\le x\le {{360}^\circ}[/latex]
[latex]\scriptsize \begin{align*}3y & =\cos \left( {\displaystyle \frac{1}{2}x} \right)\\\therefore y & =\displaystyle \frac{1}{3}\cos \left( {\displaystyle \frac{1}{2}x} \right)\text{ }\end{align*}[/latex]
[latex]\scriptsize k=\displaystyle \frac{1}{2}[/latex]. Therefore,[latex]\scriptsize \text{period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| {\displaystyle \frac{1}{2}} \right|}}={{720}^\circ}[/latex]
[latex]\scriptsize a=\displaystyle \frac{1}{3}[/latex]. Therefore, amplitude is [latex]\scriptsize \displaystyle \frac{1}{3}[/latex].[latex]\scriptsize \cos x[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{90}^\circ},0)[/latex] [latex]\scriptsize ({{180}^\circ},-1)[/latex] [latex]\scriptsize ({{270}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},1)[/latex] [latex]\scriptsize \displaystyle \frac{1}{3}\cos \left( {\displaystyle \frac{1}{2}x} \right)[/latex] [latex]\scriptsize ({{0}^\circ},\displaystyle \frac{1}{3})[/latex] [latex]\scriptsize ({{180}^\circ},0)[/latex] [latex]\scriptsize \displaystyle ({{360}^\circ},-\displaystyle \frac{1}{3})[/latex] [latex]\scriptsize ({{540}^\circ},0)[/latex] [latex]\scriptsize ({{720}^\circ},\displaystyle \frac{1}{3})[/latex] 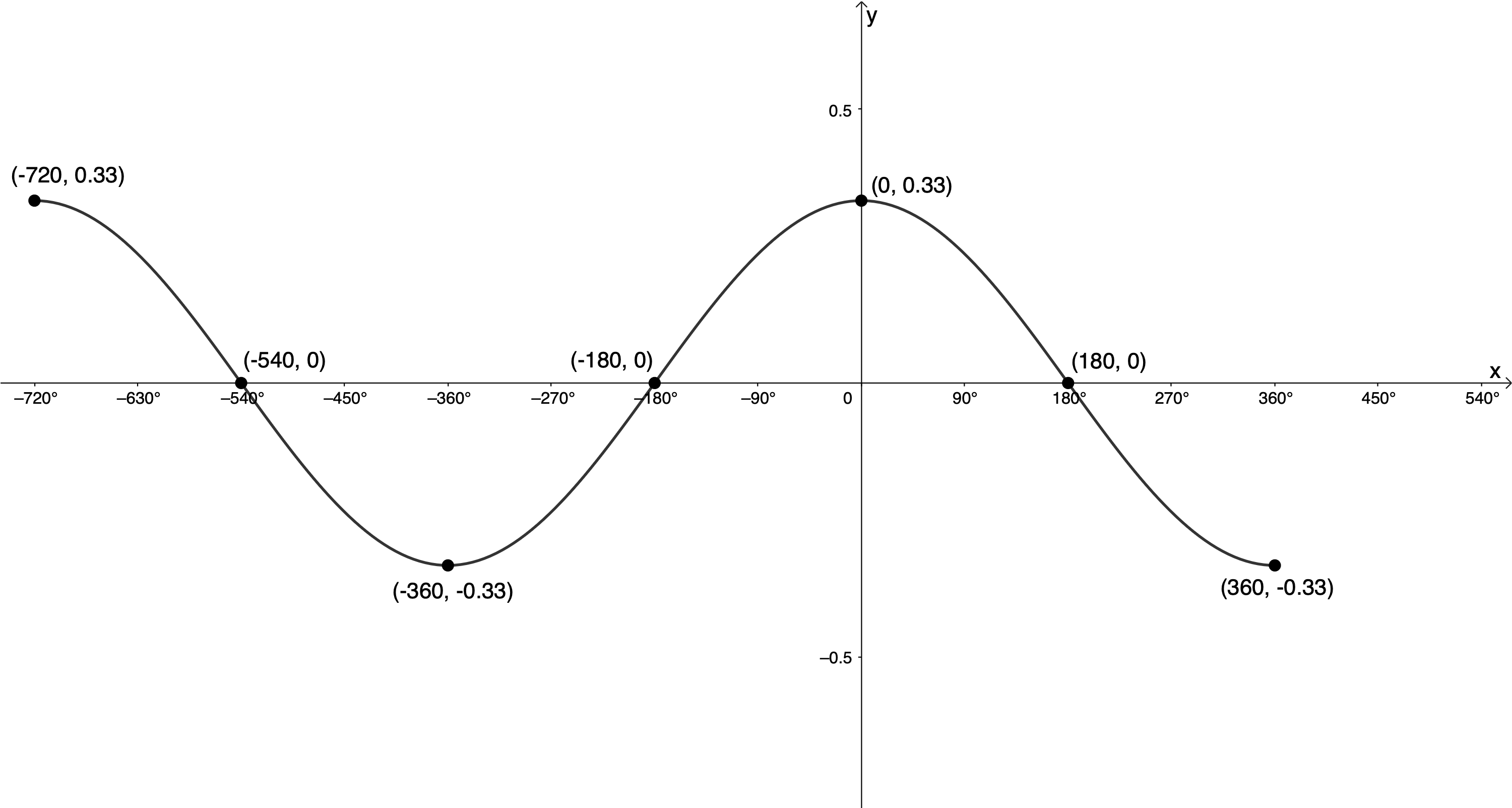
- [latex]\scriptsize g(x)=-3\cos 2x[/latex] for [latex]\scriptsize {{0}^\circ}\le x\le {{270}^\circ}[/latex]
[latex]\scriptsize k=2[/latex]. Therefore,[latex]\scriptsize \text{period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| 2 \right|}}={{180}^\circ}\text{ }[/latex]
[latex]\scriptsize a=-3[/latex]. Therefore, amplitude is [latex]\scriptsize 3[/latex] and the graph is reflected about the x-axis.[latex]\scriptsize \cos x[/latex] [latex]\scriptsize ({{0}^\circ},1)[/latex] [latex]\scriptsize ({{90}^\circ},0)[/latex] [latex]\scriptsize ({{180}^\circ},-1)[/latex] [latex]\scriptsize ({{270}^\circ},0)[/latex] [latex]\scriptsize ({{360}^\circ},1)[/latex] [latex]\scriptsize -3\cos 2x[/latex] [latex]\scriptsize ({{0}^\circ},-3)[/latex] [latex]\scriptsize ({{45}^\circ},0)[/latex] [latex]\scriptsize \displaystyle ({{90}^\circ},3)[/latex] [latex]\scriptsize ({{135}^\circ},0)[/latex] [latex]\scriptsize ({{180}^\circ},-3)[/latex] 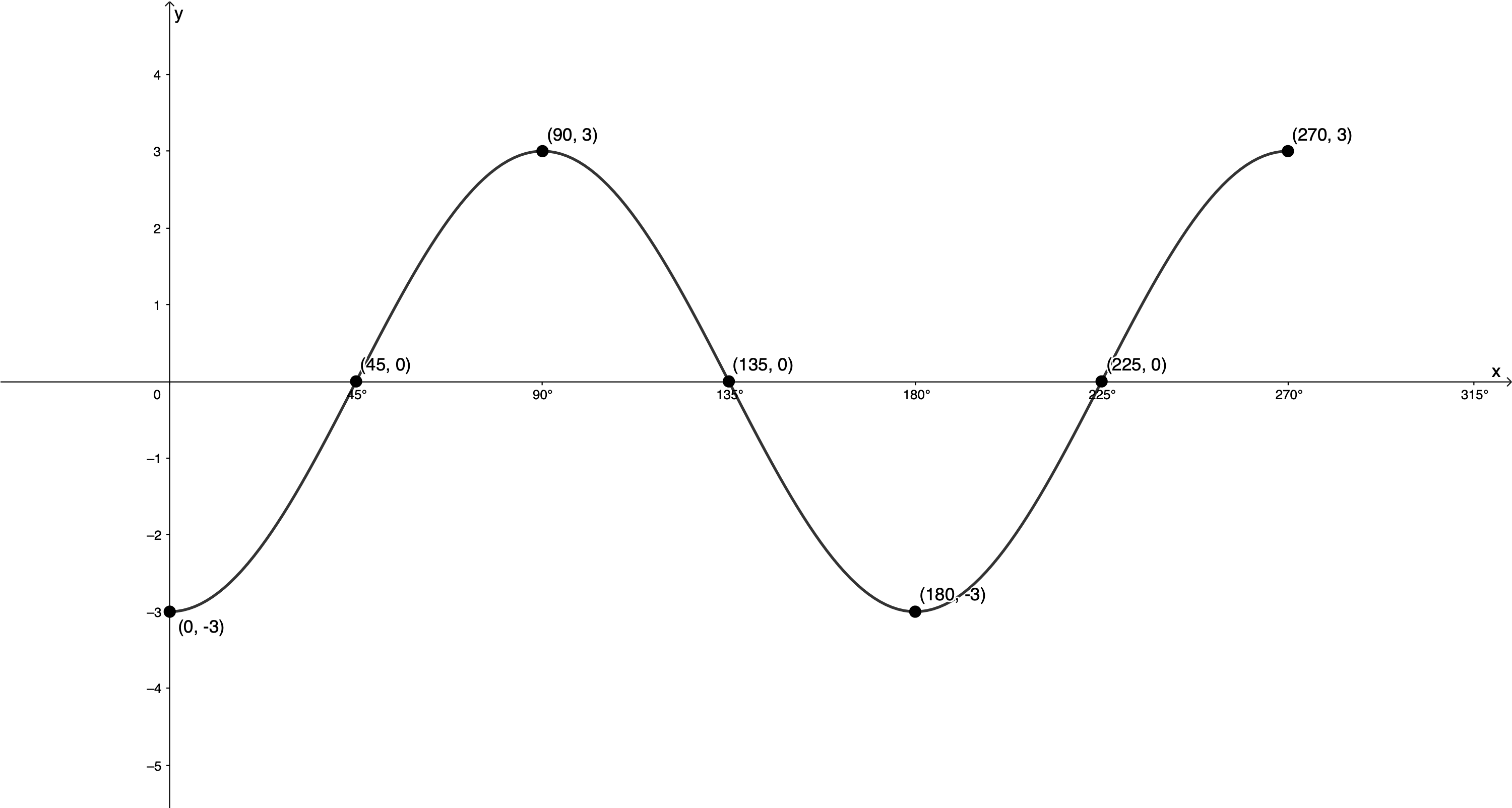
- [latex]\scriptsize 3y=\cos \left( {\displaystyle \frac{1}{2}x} \right)[/latex] for [latex]\scriptsize -{{720}^\circ}\le x\le {{360}^\circ}[/latex]
- The amplitude is [latex]\scriptsize 1[/latex] and the graph is reflected about the x-axis. Therefore, [latex]\scriptsize a=-1[/latex] and [latex]\scriptsize y=-\cos kx[/latex].
The graph completes half a period between [latex]\scriptsize -{{360}^\circ}[/latex] and [latex]\scriptsize {{360}^\circ}[/latex]. Therefore, the period is [latex]\scriptsize 2\times {{720}^\circ}=1 \ {{440}^\circ}[/latex].
[latex]\scriptsize \begin{align*}\text{Period}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\1\ {{440}^\circ}=\displaystyle \frac{{{{{360}}^\circ}}}{{\left| k \right|}}\\\therefore \left| k \right|=\displaystyle \frac{{{{{360}}^\circ}}}{{1\ {{{440}}^\circ}}}=\displaystyle \frac{1}{4}\end{align*}[/latex]
[latex]\scriptsize y=-\cos \left( {\displaystyle \frac{1}{4}x} \right)[/latex]
Media Attributions
- figure1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure4 © DHET is licensed under a CC BY (Attribution) license
- figure5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- takenote © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise9.1Q2a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise9.1Q2b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise9.1Q2c © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure6 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example9.2 © Geogebra is licensed under a CC BY (Attribution) license
- example9.3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example9.4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example9.5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise9.3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentQ2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise9.2A1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise9.2A2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise9.2A3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentA1a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentA1b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
