Unit outcomes

By the end of this unit you will be able to:

• Solve simultaneous equations algebraically where the one equation is linear and the other equation is quadratic.
• Solve simultaneous equations graphically where the one equation is linear and the other equation is quadratic.

What you should know

Before you start this unit, make sure you can:

• Solve simultaneous equations where both equations are linear. Refer to level 2 subject outcome 2.3 unit 4 if you need help with this.
• Solve quadratic equations by factorising and using the quadratic formula. Refer to unit 1, unit 2 and unit 3 in this subject outcome if you need help with this.
• Sketch linear functions. Refer to level 2 subject outcome 2.1 unit 1 if you need help with this.
• Sketch quadratic functions. Refer to level 2 subject outcomes 2.1 unit 2 and level 3 subject outcome 2.1 unit 1 if you need help with this.

Here is a short self-assessment to make sure you have the simultaneous equation skills you need to proceed with this unit.

Solve the following equations simultaneously:

1. [latex]\scriptsize 5a+3b+11=0[/latex] and [latex]\scriptsize 4b=-2a-10[/latex]
2. [latex]\scriptsize \displaystyle \frac{{x+1}}{y}=7[/latex] and [latex]\scriptsize \displaystyle \frac{x}{{y+1}}=6[/latex]

Solutions

1. [latex]\scriptsize 5a+3b+11=0\quad \quad (1)[/latex]
   [latex]\scriptsize 4b=-2a-10\quad \quad (2)[/latex]
   From (2):
   [latex]\scriptsize \begin{align*}4b & =-2a-10\\\therefore 2a & =-4b-10\\\therefore a & =-2b-5\quad (3)\end{align*}[/latex]
   Substitute (3) into (1):
   [latex]\scriptsize \begin{align*}5(-2b-5)+3b+11 & =0\\\therefore -10b-25+3b+11 & =0\\\therefore -7b & =14\\\therefore b & =-2\end{align*}[/latex]
   Substitute [latex]\scriptsize b=-2[/latex] into (3):
   [latex]\scriptsize \begin{align*}a & =-2(-2)-5\\\therefore a & =-1\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}a=-1\\b=-2\end{align*}[/latex]
2. [latex]\scriptsize \displaystyle \frac{{x+1}}{y}=7\quad \quad (1)[/latex]
   [latex]\scriptsize \displaystyle \frac{x}{{y+1}}=6\quad \quad (2)[/latex]
   From (1):
   [latex]\scriptsize \begin{align*}x+1 & =7y\\\therefore x & =7y-1\quad (3)\end{align*}[/latex]
   From (2):
   [latex]\scriptsize x=6y+6\quad \quad (4)[/latex]
   Substitute (3) into (4):
   [latex]\scriptsize \begin{align*}7y-1 & =6y+6\\\therefore y & =7\end{align*}[/latex]
   Substitute [latex]\scriptsize y=7[/latex] into (3):
   [latex]\scriptsize \begin{align*}x & =7(7)-1\\\therefore x & =48\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}x&=48\\y&=7\end{align*}[/latex]

Introduction

We learnt how to solve simultaneous equations in level 2 subject outcome 2.3 unit 4. In that unit, we only solved two equations simultaneously at a time and both equations were linear equations.

In all cases in that unit, we got two answers or one answer pair [latex]\scriptsize (x,y)[/latex] and we made the point that to solve for two unknowns, you need two equations. To solve for three unknowns, you would need three equations and so on.

We also learnt that we can solve equations simultaneously in a few different ways:

• Algebraically:
  • The substitution method requires us to express one of the unknowns in terms of the other from one of the equations and then to substitute this into the other equation.
  • The elimination method requires us to multiply through each equation by whatever constants will allow us to eliminate one of the unknowns by adding or subtracting the resulting equations.
• Graphically: The solution to simultaneous equations is the point where the graphs of the two functions intersect.

We will use all of these methods to solve simultaneous equations in this unit. The only difference is that one of the equations will be linear and the other will be quadratic. You may choose the method you are most comfortable with to solve simultaneously unless the instruction says otherwise.

Think for a moment how many answer pairs you can expect to get when you solve a linear and quadratic equation simultaneously.

Solve simultaneous equations algebraically: the substitution method

The best way to learn how to solve a linear and quadratic equation simultaneously by substitution is to work through an example.

Example 4.1

Solve for [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] in the following equations using substitution:

[latex]\scriptsize {{x}^{2}}-y=-3x-2[/latex]
[latex]\scriptsize 12y-18x=24[/latex]

Solution

We need to express one of the variables in terms of the other. When one of the equations is quadratic and the other linear, it is often best to express the variable that is not squared in terms of the other in the linear equation.

[latex]\scriptsize {{x}^{2}}-y=-3x-2\quad \quad (1)[/latex]
[latex]\scriptsize 12y-18x=24\quad \quad (2)[/latex]

From (2):
[latex]\scriptsize \begin{align*}12y-18x & =24\\\therefore 12y & =18x+24\\\therefore y & =\displaystyle \frac{{18}}{{12}}x+2\\\therefore y & =\displaystyle \frac{3}{2}x+2\quad \text{(3)}\end{align*}[/latex]
Substitute (3) into (1):
[latex]\scriptsize \begin{align*}{{x}^{2}}-\left( {\displaystyle \frac{3}{2}x+2} \right) & =-3x-2\\\therefore {{x}^{2}}-\displaystyle \frac{3}{2}x-2+3x+2 & =0\\\therefore {{x}^{2}}+\displaystyle \frac{3}{2}x & =0\\\therefore x\left( {x+\displaystyle \frac{3}{2}} \right) & =0\\\therefore x=0\text{ } & \text{or }x=-\displaystyle \frac{3}{2}\end{align*}[/latex]

Now we have two solutions for [latex]\scriptsize x[/latex]. We need to substitute these values for [latex]\scriptsize x[/latex] into any of the other equations to find the corresponding solutions for [latex]\scriptsize y[/latex].

Substitute into (3):
[latex]\scriptsize x=0[/latex]:
[latex]\scriptsize \begin{align*}y&=\displaystyle \frac{3}{2}(0)+2\\&=2\end{align*}[/latex]
[latex]\scriptsize x=-\displaystyle \frac{3}{2}[/latex]:
[latex]\scriptsize \begin{align*}y&=\displaystyle \frac{3}{2}\left( {-\displaystyle \frac{3}{2}} \right)+2\\&=-\displaystyle \frac{9}{4}+\displaystyle \frac{8}{4}\\&=-\displaystyle \frac{1}{4}\end{align*}[/latex]

Therefore [latex]\scriptsize x=0[/latex] and [latex]\scriptsize y=2[/latex] or [latex]\scriptsize x=-\displaystyle \frac{3}{2}[/latex] and [latex]\scriptsize y=-\displaystyle \frac{1}{4}[/latex]. Another way of writing the answer would be as the ordered pairs [latex]\scriptsize (0,2)[/latex] and [latex]\scriptsize (-\displaystyle \frac{3}{2},-\displaystyle \frac{1}{4})[/latex].

We can see that because one of the equations is a quadratic, the system of simultaneous equations generates two solution pairs.

Example 4.2

Solve for [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] in the following equations using substitution:

[latex]\scriptsize 6x+y={{x}^{2}}+5[/latex]
[latex]\scriptsize y=-2x+2[/latex]

Solution

[latex]\scriptsize 6x+y={{x}^{2}}+5\quad \quad (1)[/latex]
[latex]\scriptsize y=-2x+2\quad \quad (2)[/latex]

In equation (2), [latex]\scriptsize y[/latex] is already the subject of the formula so we can go straight to the substitution.

Substitute (2) into (1):
[latex]\scriptsize \begin{align*}6x+(-2x+2) & ={{x}^{2}}+5\\\therefore 6x-2x+2-{{x}^{2}}-5 & =0\\\therefore -{{x}^{2}}+4x-3 & =0\\\therefore {{x}^{2}}-4x+3 & =0\\\therefore (x-3)(x-1) & =0\\\therefore x=3\text{ } & \text{or }x=1\end{align*}[/latex]
Substitute into (2):
[latex]\scriptsize x=3[/latex]:
[latex]\scriptsize \begin{align*}y&=-2(3)+2\\&=-4\end{align*}[/latex]
[latex]\scriptsize x=1[/latex]:
[latex]\scriptsize \begin{align*}y&=-2(1)+2\\&=0\end{align*}[/latex]

Therefore, [latex]\scriptsize x=3[/latex] and [latex]\scriptsize y=-4[/latex] or [latex]\scriptsize x=1[/latex] and [latex]\scriptsize y=0[/latex].

Exercise 4.1

Solve the following simultaneous equations using the substitution method:

1. [latex]\scriptsize y={{x}^{2}}+2x-4[/latex] and [latex]\scriptsize y=2x[/latex]
2. [latex]\scriptsize y=2{{x}^{2}}+7x-4[/latex] and [latex]\scriptsize y=2x-1[/latex]
3. [latex]\scriptsize 5{{x}^{2}}+8y=104[/latex] and [latex]\scriptsize 4x+y=19[/latex]

The full solutions are at the end of the unit.

Solve simultaneous equations algebraically: the elimination method

The next example illustrates how to solve a system of simultaneous equations using the elimination method.

Example 4.3

Solve for [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] in the following equations using elimination:

[latex]\scriptsize y={{x}^{2}}+5x-24[/latex]
[latex]\scriptsize y-x+19=0[/latex]

Solution

[latex]\scriptsize y={{x}^{2}}+5x-24\quad \quad (1)[/latex]
[latex]\scriptsize y-x+19=0\quad \quad (2)[/latex]

From 2:
[latex]\scriptsize \begin{align*}y-x+19 & =0\\\therefore y & =x-19\quad (3)\end{align*}[/latex]

We do not need to multiply through either of the equations in order to create an unknown to eliminate. Both equations contain [latex]\scriptsize y[/latex]. This is the unknown that we will eliminate.
First we subtract equation 3 from equation 1:
(1) – (3):
[latex]\scriptsize \begin{align*} y&=x^2+5x-24\\ -\underline{\left(y&=~~~~~~~~~x-19\right)}&&\text{It is very important to line up your terms correctly}\\ 0&=x^2+4x-5 \end{align*}[/latex]

[latex]\scriptsize \begin{align*}{{x}^{2}}+4x-5 & =0\\\therefore (x-1)(x+5) & =0\\\therefore x=1\text{ } & \text{or }x=-5\end{align*}[/latex]

Now we can substitute both our vales of [latex]\scriptsize x[/latex] into any of the other equations to find the corresponding values for [latex]\scriptsize y[/latex].

Substitute into (3):
[latex]\scriptsize x=1[/latex]:
[latex]\scriptsize \begin{align*}y&=1-19\\&=-18\end{align*}[/latex]
[latex]\scriptsize x=-5[/latex]:
[latex]\scriptsize \begin{align*}y&=-5-19\\&=-24\end{align*}[/latex]
Therefore [latex]\scriptsize x=1[/latex] and [latex]\scriptsize y=-18[/latex] or [latex]\scriptsize x=-5[/latex] and [latex]\scriptsize y=-24[/latex]

Most of the time solving simultaneous equations algebraically will be easier using substitution but you are free to use the elimination method if you like.

Exercise 4.2

Solve the following systems of simultaneous equations algebraically, leaving your answer in simplest surd form if necessary:

1. [latex]\scriptsize y=-x+5[/latex] and [latex]\scriptsize y={{x}^{2}}-3x+5[/latex]
2. [latex]\scriptsize y-{{x}^{2}}=6-5x[/latex] and [latex]\scriptsize y+1=x[/latex]
3. [latex]\scriptsize 4y=2x+2[/latex] and [latex]\scriptsize y+5=2{{x}^{2}}-3x[/latex]
4. [latex]\scriptsize a-2b=-1[/latex] and [latex]\scriptsize a-12b=2({{b}^{2}}-2)[/latex]
5. [latex]\scriptsize 3{{x}^{2}}-4x=y-1[/latex] and [latex]\scriptsize 3x=4y+2[/latex]

The full solutions are at the end of the unit.

Solve simultaneous equations graphically

We said in the introduction that the graphical solution to simultaneous equations is the point where the functions intersect. Remember an equation like [latex]\scriptsize y={{x}^{2}}+2x+1[/latex] is really a function. If you think about a parabola and a straight line, it makes sense why we usually get two solution pairs. Most of the time, the straight line will intersect the parabola in two places.

Example 4.4

Solve for [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] in the following equations graphically:

[latex]\scriptsize 6x+y={{x}^{2}}+5[/latex]
[latex]\scriptsize y=-2x+2[/latex]

Solution

This is the same system of simultaneous equations we solved in Example 4.2 so we know that the solution is [latex]\scriptsize x=3[/latex] and [latex]\scriptsize y=-4[/latex] or [latex]\scriptsize x=1[/latex] and [latex]\scriptsize y=0[/latex]. We can represent the solution as the coordinates of two points on the Cartesian plane – [latex]\scriptsize (3,-4)[/latex] and [latex]\scriptsize (1,0)[/latex]. Let’s see how we can arrive at the same solution graphically.

Step 1: Get the functions in standard form
To begin with, we need to express both equations in standard form ([latex]\scriptsize y=mx+c/y=ax+q[/latex] and [latex]\scriptsize y=a{{x}^{2}}+bx+c/y=a{{(x+p)}^{2}}+q[/latex]) so that we can sketch the functions. The linear equation is already in standard form.

[latex]\scriptsize 6x+y={{x}^{2}}+5\quad \qhad (1)[/latex]
[latex]\scriptsize y=-2x+2\quad \quad (2)[/latex]

From (1):
[latex]\scriptsize \begin{align*}6x+y={{x}^{2}}+5\\\therefore y={{x}^{2}}-6x+5\quad (3)\end{align*}[/latex]

Step 2: Sketch the functions
Next, we need to sketch both functions on the same set of axes. We are not going to go through all the steps to sketching functions here. Refer to the section on prior learning above if you need help with sketching linear and quadratic functions.

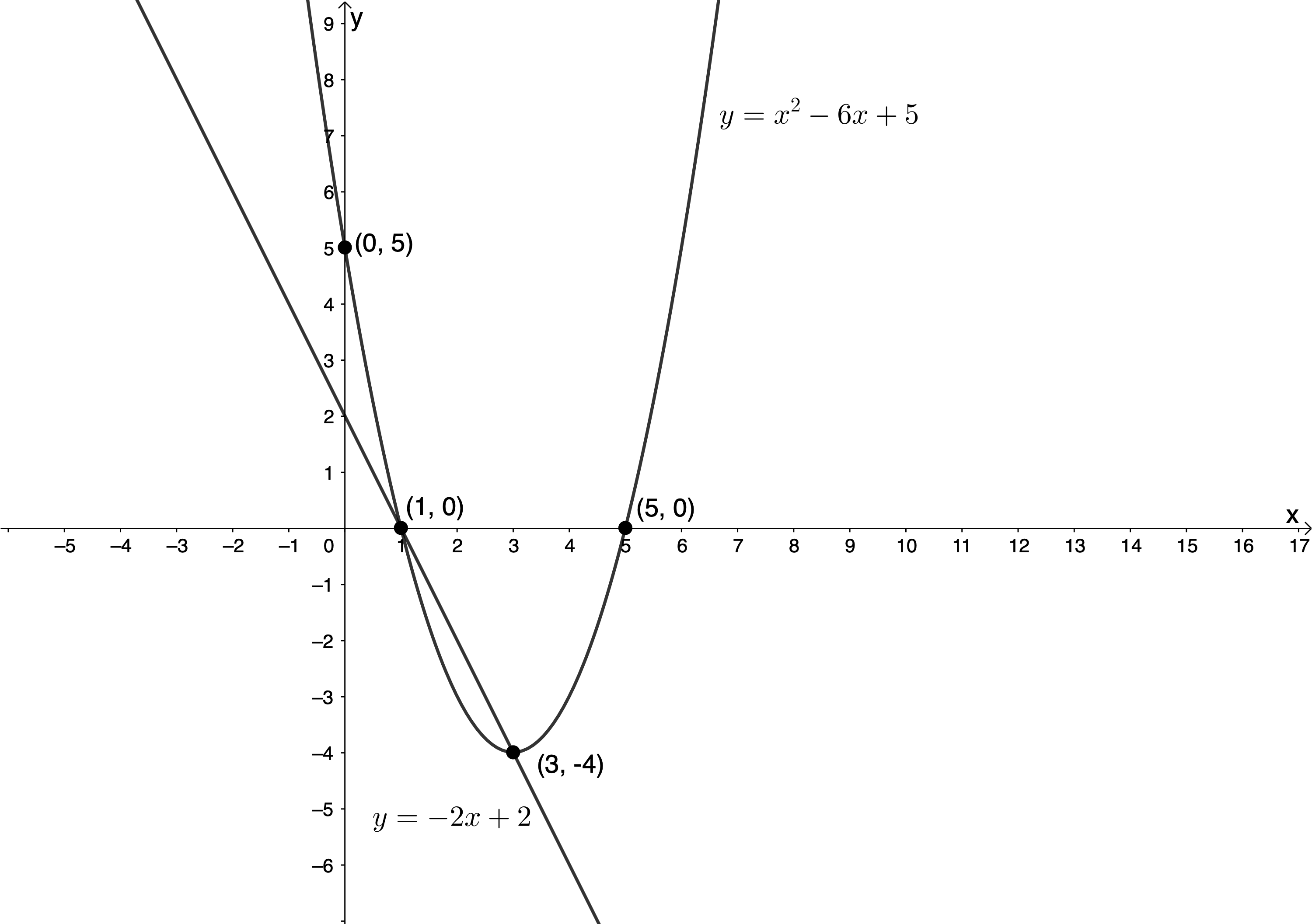
Step 3: Read off the solutions (the points of intersection)
The solution is [latex]\scriptsize (1,0)[/latex] or [latex]\scriptsize (3,-4)[/latex]. Notice that this is exactly the same result we got when solving algebraically.

Exercise 4.3

Questions 2. and 3. are taken from Everything Maths Grade 11 Exercise 2 – 9.

Solve the following systems of equations graphically. Check your solutions algebraically.

1. [latex]\scriptsize -2{{x}^{2}}=y[/latex]
   [latex]\scriptsize y-x=-1[/latex]
2. [latex]\scriptsize {{x}^{2}}-1-y=0[/latex]
   [latex]\scriptsize y+x-5=0[/latex]
3. [latex]\scriptsize x+y-10=0[/latex]
   [latex]\scriptsize {{x}^{2}}-2-y=0[/latex]

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to solve a system of two simultaneous equations algebraically where one of the equations is linear and the other is quadratic.
• How to solve a system of two simultaneous equations graphically where one of the equations is linear and the other is quadratic.

Unit 4: Assessment

Suggested time to complete: 50 minutes

1. Solve the following systems of simultaneous equations algebraically:
   1. [latex]\scriptsize y=3x+2[/latex]
      [latex]\scriptsize y=3{{x}^{2}}+6x-4[/latex]
   2. [latex]\scriptsize 2x-y=1[/latex]
      [latex]\scriptsize y-{{x}^{2}}=-3x+3[/latex]
   3. [latex]\scriptsize y={{(x-2)}^{2}}-9[/latex]
      [latex]\scriptsize y=2x+4[/latex]
2. Show the solution to question 1.b. above graphically.
3. Solve the following system of simultaneous equations graphically:
   [latex]\scriptsize {{x}^{2}}-4x=y-4[/latex]
   [latex]\scriptsize y+3x=6[/latex]

The full solutions are at the end of the unit.

Unit 4: Solutions

Exercise 4.1

1. [latex]\scriptsize y={{x}^{2}}+2x-3\quad \quad (1)[/latex]
   [latex]\scriptsize y=2x\quad \quad (2)[/latex]
   Substitute (2) into (1):
   [latex]\scriptsize \begin{align*}2x & ={{x}^{2}}+2x-4\\\therefore {{x}^{2}} & =4\\\therefore x & =\pm 2\end{align*}[/latex]
   Substitute into (2):
   [latex]\scriptsize x=2[/latex]:             [latex]\scriptsize x=-2[/latex]:
   [latex]\scriptsize y=4[/latex]             [latex]\scriptsize y=-4[/latex]
   [latex]\scriptsize x=2[/latex] and [latex]\scriptsize y=4[/latex] or [latex]\scriptsize x=-2[/latex] and [latex]\scriptsize y=-4[/latex]
2. [latex]\scriptsize y=2{{x}^{2}}+7x-4\quad \quad (1)[/latex]
   [latex]\scriptsize y=2x-1\quad \quad (2)[/latex]
   Substitute (2) into (1):
   [latex]\scriptsize \begin{align*}2x-1 & =2{{x}^{2}}+7x-4\\\therefore 2{{x}^{2}}+5x-3 & =0\\\therefore (2x-1)(x+3) & =0\\\therefore x=\displaystyle \frac{1}{2}\text{ } & \text{or }x=-3\end{align*}[/latex]
   Substitute into (2):
   [latex]\scriptsize x=\displaystyle \frac{1}{2}[/latex]:               [latex]\scriptsize x=-3[/latex]:
   [latex]\scriptsize y=2\left( {\displaystyle \frac{1}{2}} \right)-1=0[/latex]       [latex]\scriptsize y=2(-3)-1=-7[/latex]
   [latex]\scriptsize x=\displaystyle \frac{1}{2}[/latex] and [latex]\scriptsize y=0[/latex] or [latex]\scriptsize x=-3[/latex] and [latex]\scriptsize y=-7[/latex]
3. [latex]\scriptsize 5{{x}^{2}}+8y=104\quad \quad (1)[/latex]
   [latex]\scriptsize 4x+y=19\quad \quad (2)[/latex]
   From (2):
   [latex]\scriptsize \begin{align*}4x+y & =19\\\therefore y & =19-4x\quad \quad (3)\end{align*}[/latex]
   Substitute (3) into (1):
   [latex]\scriptsize \begin{align*}5{{x}^{2}}+8(19-4x) & =104\\\therefore 5{{x}^{2}}+152-32x & =104\\\therefore 5{{x}^{2}}-32x+48 & =0\\\therefore (5x-12)(x-4) & =0\\\therefore x=\displaystyle \frac{{12}}{5}\text{ } & \text{or }x=4\end{align*}[/latex]
   Substitute into (3):
   [latex]\scriptsize x=\displaystyle \frac{{12}}{5}[/latex]:                 [latex]\scriptsize x=4[/latex]:
   [latex]\scriptsize \begin{align*}y&=19-4\left( {\displaystyle \frac{{12}}{5}} \right)\\&=19-\displaystyle \frac{{48}}{5}\\&=\displaystyle \frac{{95-48}}{5}\\&=\displaystyle \frac{{47}}{5}\end{align*}[/latex]         [latex]\scriptsize \begin{align*}y&=19-4(4)\\&=19-16\\&=3\end{align*}[/latex]
   [latex]\scriptsize x=\displaystyle \frac{{12}}{5}[/latex] and [latex]\scriptsize y=\displaystyle \frac{{47}}{5}[/latex] or [latex]\scriptsize x=4[/latex] and [latex]\scriptsize y=3[/latex]

Back to Exercise 4.1

Exercise 4.2

1. [latex]\scriptsize y=-x+5\quad \quad (1)[/latex]
   [latex]\scriptsize y={{x}^{2}}-3x+5\quad \quad (2)[/latex]
   Substitute (1) into (2):
   [latex]\scriptsize \begin{align*}-x+5 & ={{x}^{2}}-3x+5\\\therefore {{x}^{2}}-2x & =0\\\therefore x(x-2) & =0\\\therefore x=0\text{ } & \text{or }x=2\end{align*}[/latex]
   Substitute into (1):
   [latex]\scriptsize x=0[/latex]:           [latex]\scriptsize x=2[/latex]:
   [latex]\scriptsize \begin{align*}y&=0+5\\&=5\end{align*}[/latex]       [latex]\scriptsize \begin{align*}y&=-2+5\\&=3\end{align*}[/latex]
   [latex]\scriptsize x=0[/latex] and [latex]\scriptsize y=5[/latex] or [latex]\scriptsize x=2[/latex] and [latex]\scriptsize y=3[/latex]
2. [latex]\scriptsize y-{{x}^{2}}=6-5x\quad \quad (1)[/latex]
   [latex]\scriptsize y+1=x\quad \quad (2)[/latex]
   From (2):
   [latex]\scriptsize \begin{align*}y+1 & =x\\\therefore y & =x-1\quad (3)\end{align*}[/latex]
   Substitute (3) into (1):
   [latex]\scriptsize \begin{align*}(x-1)-{{x}^{2}} & =6-5x\\\therefore {{x}^{2}}-6x+7 & =0\\a=1,b=-6,c=7 & \end{align*}[/latex]
   [latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(-6)\pm \sqrt{{{{{(-6)}}^{2}}-4(1)(7)}}}}{{2(1)}}\\&=\displaystyle \frac{{6\pm \sqrt{{36-28}}}}{2}\\&=\displaystyle \frac{{6\pm \sqrt{8}}}{2}\\&=\displaystyle \frac{{6\pm 2\sqrt{2}}}{2}\\&=3\pm \sqrt{2}\end{align*}[/latex]
   Substitute into (3):
   [latex]\scriptsize x=3+\sqrt{2}[/latex]:           [latex]\scriptsize x=3-\sqrt{2}[/latex]:
   [latex]\scriptsize y=3+\sqrt{2}-1[/latex]         [latex]\scriptsize y=3-\sqrt{2}-1[/latex]
   [latex]\scriptsize x=3+\sqrt{2}[/latex] and [latex]\scriptsize y=3+\sqrt{2}-1[/latex] or [latex]\scriptsize x=3-\sqrt{2}[/latex] and [latex]\scriptsize y=3-\sqrt{2}-1[/latex]
3. [latex]\scriptsize 4y=2x+2\quad \quad (1)[/latex]
   [latex]\scriptsize y+5=2{{x}^{2}}-3x\quad \quad (2)[/latex]
   From (1):
   [latex]\scriptsize \begin{align*}4y & =2x+2\\\therefore y & =\displaystyle \frac{{2x+2}}{4}\\&=\displaystyle \frac{{2(x+1)}}{4}\\&=\displaystyle \frac{{x+1}}{2}\quad (3)\end{align*}[/latex]
   Substitute (3) into (2):
   [latex]\scriptsize \begin{align*}\left( {\displaystyle \frac{{x+1}}{2}} \right)+5 & =2{{x}^{2}}-3x\\\therefore x+1+10 & =4{{x}^{2}}-6x\\\therefore 4{{x}^{2}}-7x-11 & =0\\\therefore (4x-11)(x+1) & =0\\\therefore x=\displaystyle \frac{{11}}{4}\text{ } & \text{or }x=-1\end{align*}[/latex]
   Substitute into (3):
   [latex]\scriptsize x=\displaystyle \frac{{11}}{4}[/latex]:
   [latex]\scriptsize \begin{align*}y&=\displaystyle \frac{{\displaystyle \frac{{11}}{4}+1}}{2}\\&=\displaystyle \frac{{\displaystyle \frac{{15}}{4}}}{2}\\&=\displaystyle \frac{{15}}{4}\times \displaystyle \frac{1}{2}\\&=\displaystyle \frac{{15}}{8}\end{align*}[/latex]
   [latex]\scriptsize x=-1[/latex]:
   [latex]\scriptsize \begin{align*}y=&\displaystyle \frac{{-1+1}}{2}\\&=0\end{align*}[/latex]
   [latex]\scriptsize x=\displaystyle \frac{{11}}{4}[/latex] and [latex]\scriptsize y=\displaystyle \frac{{15}}{8}[/latex] or [latex]\scriptsize x=-1[/latex] and [latex]\scriptsize y=0[/latex]
4. [latex]\scriptsize a-2b=-1\quad \quad (1)[/latex]
   [latex]\scriptsize a-12b=2({{b}^{2}}-2)\quad \quad (2)[/latex]
   From (1):
   [latex]\scriptsize \begin{align*}a-2b & =-1\\\therefore a & =2b-1\quad (3)\end{align*}[/latex]
   Substitute (3) into (2):
   [latex]\scriptsize \begin{align*}(2b-1)-12b & =2({{b}^{2}}-2)\\\therefore 2b-1-12b & =2{{b}^{2}}-4\\\therefore 2{{b}^{2}}+10b-3 & =0\\a=2,b=10,c=-3 & \end{align*}[/latex]
   [latex]\scriptsize \begin{align*}b & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\quad \text{Don }\!\!'\!\!\text{ t confuse the unknown }b\text{ for the coefficient }b\\\therefore b & =\displaystyle \frac{{-(10)\pm \sqrt{{{{{(10)}}^{2}}-4(2)(-3)}}}}{{2(2)}}\\&=\displaystyle \frac{{10\pm \sqrt{{100+24}}}}{4}\\&=\displaystyle \frac{{10\pm \sqrt{{124}}}}{4}\\&=\displaystyle \frac{{10\pm 2\sqrt{{31}}}}{4}\\&=\displaystyle \frac{{5\pm \sqrt{{31}}}}{2}\end{align*}[/latex]
   Substitute into (3):
   [latex]\scriptsize b=\displaystyle \frac{{5+\sqrt{{31}}}}{2}[/latex]:                 [latex]\scriptsize b=\displaystyle \frac{{5-\sqrt{{31}}}}{2}[/latex]:
   [latex]\scriptsize \begin{align*}a&=2\left( {\displaystyle \frac{{5+\sqrt{{31}}}}{2}} \right)-1\\&=5+\sqrt{{31}}-1\\&=4+\sqrt{{31}}\end{align*}[/latex]      [latex]\scriptsize \begin{align*}a&=2\left( {\displaystyle \frac{{5-\sqrt{{31}}}}{2}} \right)-1\\&=5-\sqrt{{31}}-1\\&=4-\sqrt{{31}}\end{align*}[/latex]
   [latex]\scriptsize b=\displaystyle \frac{{5+\sqrt{{31}}}}{2}[/latex] and [latex]\scriptsize a=4+\sqrt{{31}}[/latex] or [latex]\scriptsize b=\displaystyle \frac{{5-\sqrt{{31}}}}{2}[/latex] and [latex]\scriptsize a=4-\sqrt{{31}}[/latex]

Back to Exercise 4.2

Exercise 4.3

1. [latex]\scriptsize -2{{x}^{2}}=y\quad \quad (1)[/latex]
   [latex]\scriptsize y-x=-1\quad \quad (2)[/latex]
   From (2): [latex]\scriptsize y=x-1[/latex]
   
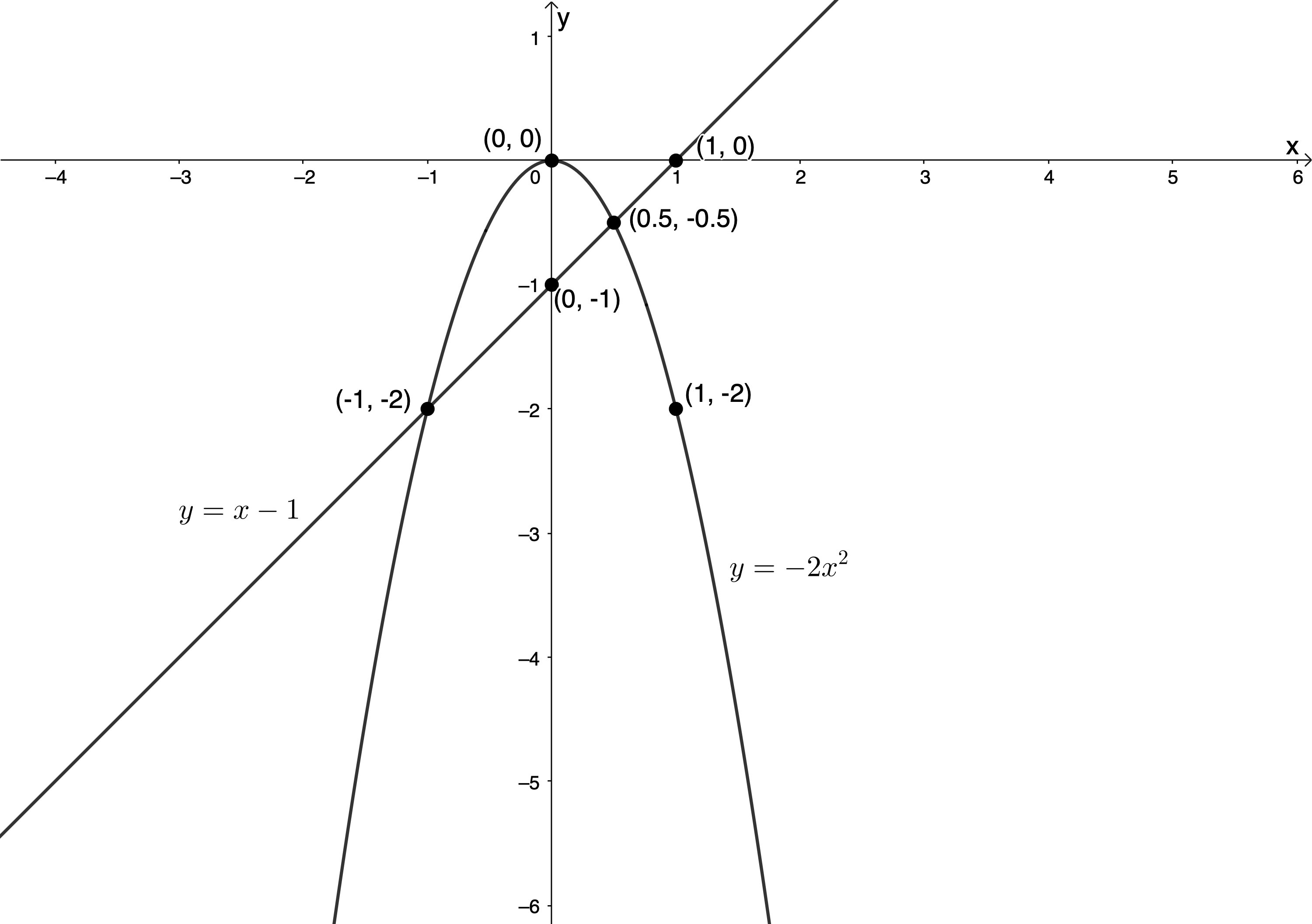
   [latex]\scriptsize (-1,-2)[/latex] or [latex]\scriptsize (\displaystyle \frac{1}{2},-\displaystyle \frac{1}{2})[/latex]
2. [latex]\scriptsize {{x}^{2}}-1-y =0\quad \quad (1)[/latex]
   [latex]\scriptsize y+x-5=0\quad \quad (2)[/latex]
   From (1):
   [latex]\scriptsize \begin{align*}{{x}^{2}}-1-y & =0\\\therefore y & ={{x}^{2}}-1\end{align*}[/latex]
   From (2):
   [latex]\scriptsize y=-x+5[/latex]
   
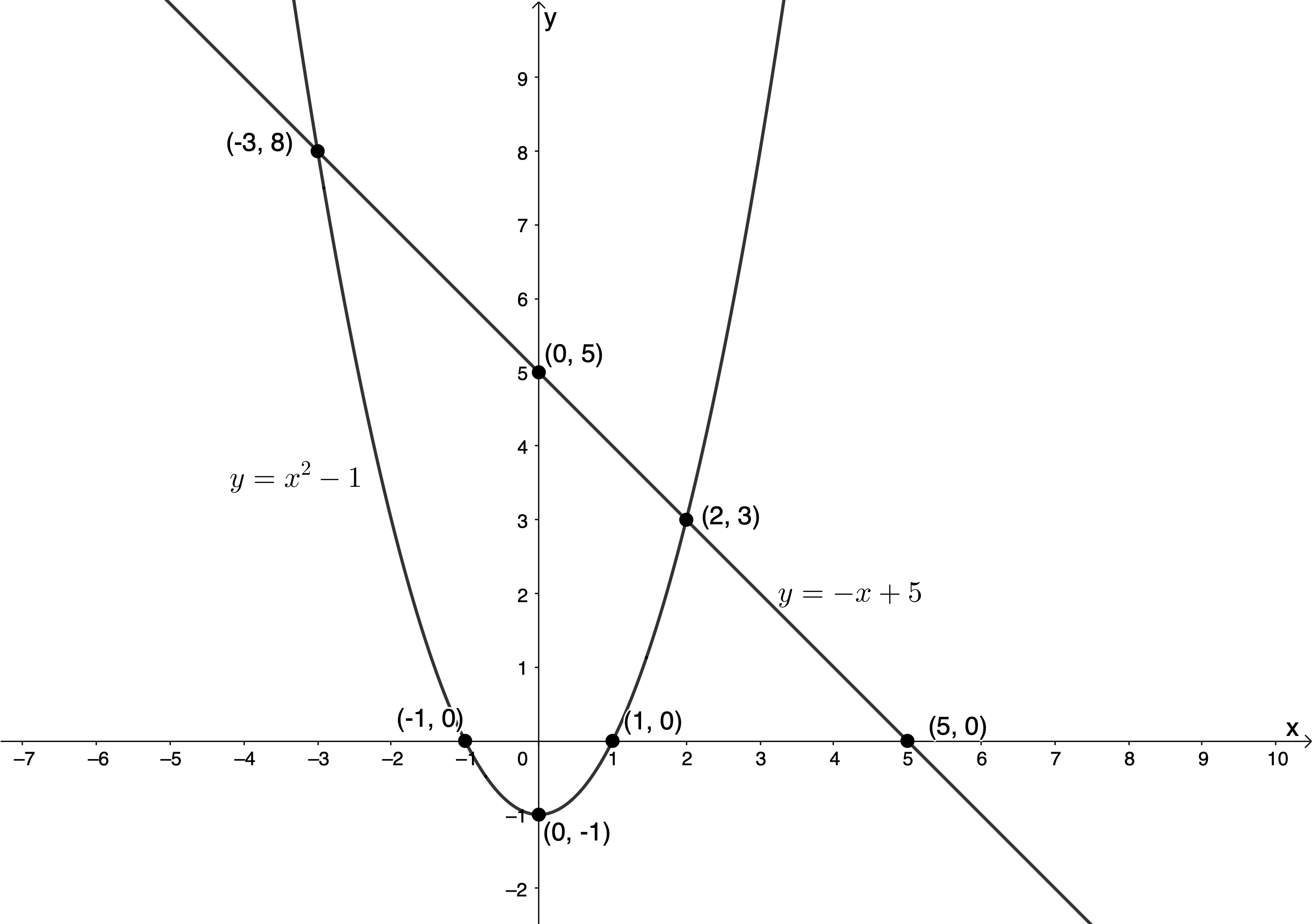
   [latex]\scriptsize (2,3)[/latex] or [latex]\scriptsize (-3,8)[/latex]
3. [latex]\scriptsize x+y-10=0\quad \quad (1)[/latex]
   [latex]\scriptsize {{x}^{2}}-2-y=0\quad \quad (2)[/latex]
   From (1):
   [latex]\scriptsize \begin{align*}x+y-10 & =0\\\therefore y & =-x+10\end{align*}[/latex]
   From (2):
   [latex]\scriptsize \begin{align*}{{x}^{2}}-2-y & =0\\\therefore y & ={{x}^{2}}-2\end{align*}[/latex]
   
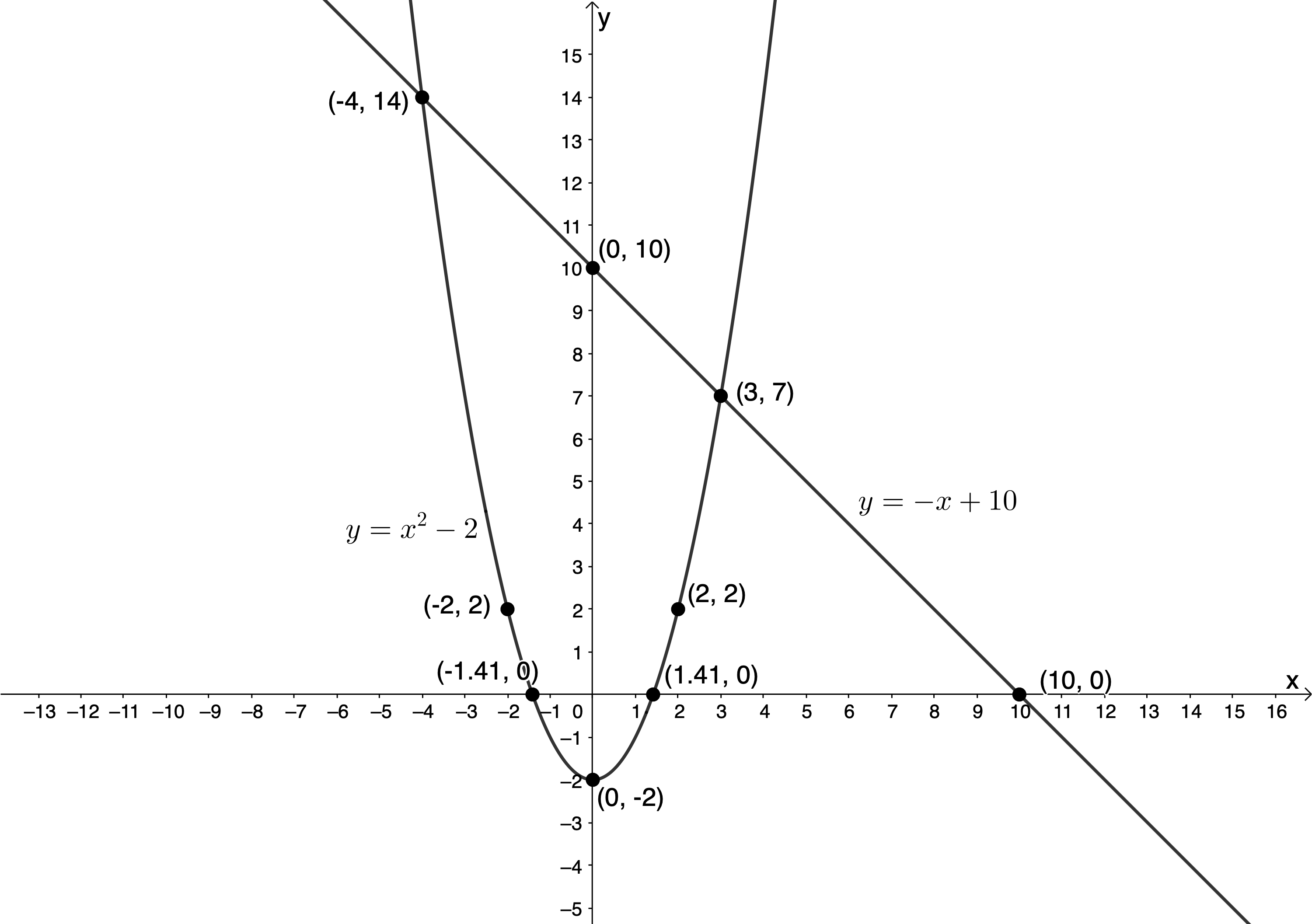
   [latex]\scriptsize (3,7)[/latex] or [latex]\scriptsize (-4,14)[/latex]

Back to Exercise 4.3

Unit 4: Assessment

1. .
   1. [latex]\scriptsize y=3x+2\quad \quad (1)[/latex]
      [latex]\scriptsize y=3{{x}^{2}}+6x-4\quad \quad (2)[/latex]
      Substitute (1) into (2):
      [latex]\scriptsize \begin{align*}3x+2 & =3{{x}^{2}}+6x-4\\\therefore 3{{x}^{2}}+3x-6 & =0\\\therefore (3x-3)(x+2) & =0\\\therefore x=1\text{ } & \text{or }x=-2\end{align*}[/latex]
      Substitute into (1):
      [latex]\scriptsize x=1[/latex]:             [latex]\scriptsize x=-2[/latex]:
      [latex]\scriptsize \begin{align*}y&=3(1)+2\\&=5\end{align*}[/latex]       [latex]\scriptsize \begin{align*}y&=3(-2)+2\\&=-4\end{align*}[/latex]
      [latex]\scriptsize x=1[/latex] and [latex]\scriptsize y=5[/latex] or [latex]\scriptsize x=-2[/latex] and [latex]\scriptsize y=-4[/latex]
   2. [latex]\scriptsize 2x-y=1\quad \quad (1)[/latex]
      [latex]\scriptsize y-{{x}^{2}}=-3x+3\quad \quad (2)[/latex]
      From (1):
      [latex]\scriptsize \begin{align*}2x-y & =1\\\therefore y & =2x-1\quad (3)\end{align*}[/latex]
      Substitute (3) into (2):
      [latex]\scriptsize \begin{align*}(2x-1)-{{x}^{2}} & =-3x+3\\\therefore {{x}^{2}}-5x+4 & =0\\\therefore (x-1)(x-4) & =0\\\therefore x=1\text{ } & \text{or }x=4\end{align*}[/latex]
      Substitute into (3):
      [latex]\scriptsize x=1[/latex]:               [latex]\scriptsize x=4[/latex]:
      [latex]\scriptsize \begin{align*}y&=2(1)-1\\&=1\end{align*}[/latex]         [latex]\scriptsize \begin{align*}y&=2(4)-1\\&=7\end{align*}[/latex]
      [latex]\scriptsize x=1[/latex] and [latex]\scriptsize y=1[/latex] or [latex]\scriptsize x=4[/latex] and [latex]\scriptsize y=7[/latex]
   3. [latex]\scriptsize y={{(x-2)}^{2}}-9\quad \quad (1)[/latex]
      [latex]\scriptsize y=2x+4\quad \quad (2)[/latex]
      Substitute (2) into (1):
      [latex]\scriptsize \begin{align*}2x+4 & ={{(x-2)}^{2}}-9\\\therefore 2x+4 & ={{x}^{2}}-4x+4-9\\\therefore {{x}^{2}}-6x-9 & =0\\a=1,b=-6,c=-9 & \end{align*}[/latex]
      [latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(-6)\pm \sqrt{{{{{(-6)}}^{2}}-4(1)(-9)}}}}{{2(1)}}\\&=\displaystyle \frac{{6\pm \sqrt{{36+36}}}}{2}\\&=\displaystyle \frac{{6\pm \sqrt{{72}}}}{2}\\&=\displaystyle \frac{{6\pm 6\sqrt{2}}}{2}\\&=3\pm 3\sqrt{2}\end{align*}[/latex]
      Substitute into (2):
      [latex]\scriptsize x=3+3\sqrt{2}[/latex]:                 [latex]\scriptsize x=3-3\sqrt{2}[/latex]:
      [latex]\scriptsize \begin{align*}y&=2\left( {3+3\sqrt{2}} \right)+4\\&=6+6\sqrt{2}+4\\&=10+6\sqrt{2}\end{align*}[/latex]           [latex]\scriptsize \begin{align*}y&=2\left( {3-3\sqrt{2}} \right)+4\\&=6-6\sqrt{2}+4\\&=10-6\sqrt{2}\end{align*}[/latex]
      [latex]\scriptsize x=3+3\sqrt{2}[/latex] and [latex]\scriptsize y=10+6\sqrt{2}[/latex] or [latex]\scriptsize x=3-3\sqrt{2}[/latex] and [latex]\scriptsize y=10-6\sqrt{2}[/latex]
2. [latex]\scriptsize 2x-y=1\quad \quad (1)[/latex]
   [latex]\scriptsize y-{{x}^{2}}=-3x+3\quad \quad (2)[/latex]
   From (1):
   [latex]\scriptsize \begin{align*}2x-y & =1\\\therefore y & =2x-1\end{align*}[/latex]
   From (2):
   [latex]\scriptsize \begin{align*}y-{{x}^{2}} & =-3x+3\\\therefore y & ={{x}^{2}}-3x+3\end{align*}[/latex]
   
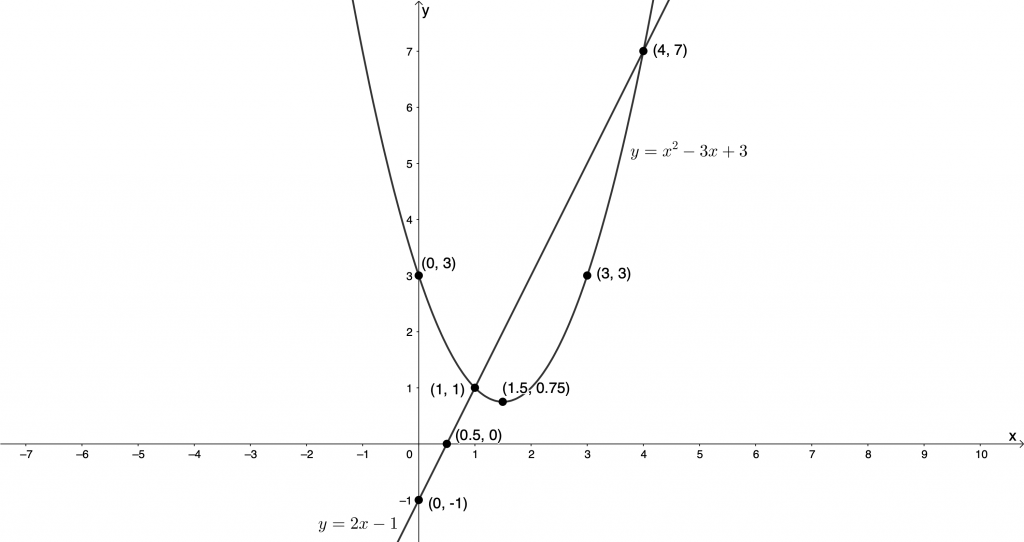
   [latex]\scriptsize (4,7)[/latex] or [latex]\scriptsize (1,1)[/latex]
3. [latex]\scriptsize {{x}^{2}}-4x=y-4\quad \quad (1)[/latex]
   [latex]\scriptsize y+3x=6\quad \quad (2)[/latex]
   From (1):
   [latex]\scriptsize \begin{align*}{{x}^{2}}-4x & =y-4\\\therefore y & ={{x}^{2}}-4x+4\end{align*}[/latex]
   From (2):
   [latex]\scriptsize \begin{align*}y+3x & =6\\\therefore y & =-3x+6\end{align*}[/latex]
   
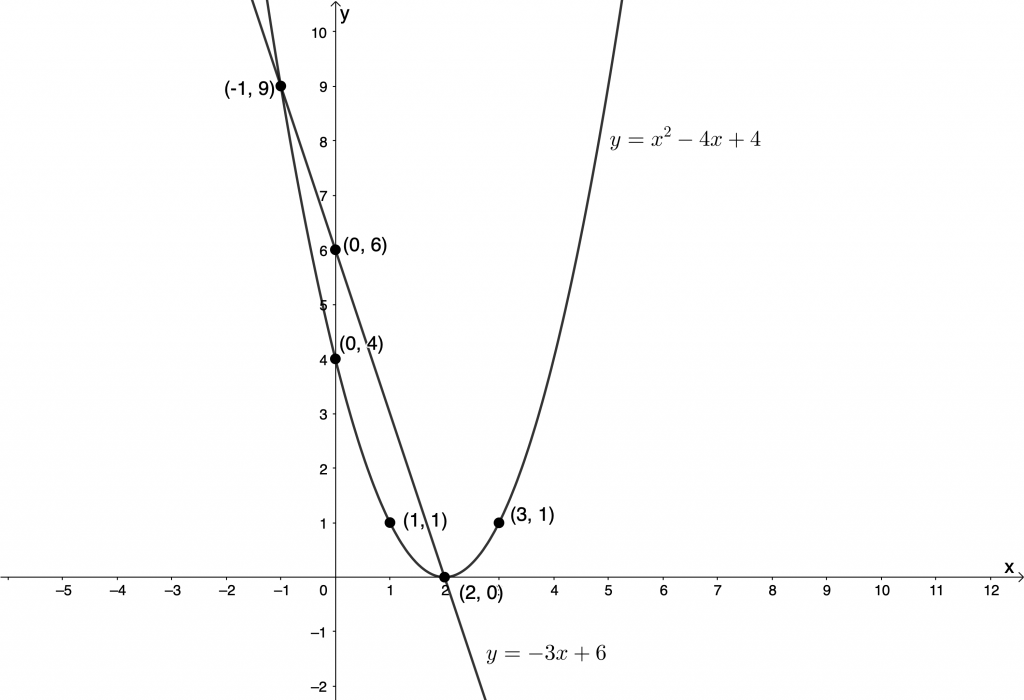
   [latex]\scriptsize (-1,9)[/latex] or [latex]\scriptsize (2,0)[/latex]

Back to Unit 4: Assessment