Functions and algebra: Investigate and use instantaneous rate of change
Unit 2: Find the derivative by first principles
Natashia Bearam-Edmunds
Unit outcomes
By the end of this unit you will be able to:
- Develop an intuitive understanding of the gradient at a point.
- Differentiate using first principles.
What you should know
Before you start this unit, make sure you can:
- Find limits of a function. To revise finding limits of a function see unit 1 of this subject outcome.
Introduction
It is widely agreed that calculus was developed independently by Sir Isaac Newton and Gottfried Leibniz in the 17th century. Since neither of them published their work as soon as they discovered their results, there is no clear indication of who discovered calculus first.

Calculus makes the study and comparison of infinitesimal (very, very, very small) changes of one quantity with respect to another possible. This has important applications in many sciences including engineering, biology, chemistry and physics.
Now that we have a basic understanding of a limit and have learnt how to compute limits (unit 1 of this subject outcome), we are ready to begin the study of calculus.
Gradient at a point on a curve
We saw in level 2 subject outcome 2.3 unit 1 that for linear graphs, it is easy to determine the slope or gradient of the graph by dividing the change in y-values by the change in x-values between the same two points.
Recall that for straight lines [latex]\scriptsize m=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex] and that the gradient of a straight line is constant between any two points on the graph.
With curved graphs the gradient changes at every point on the curve so we need to work with the average gradient. The average gradient between two points is equal to the gradient of a straight line, called a , drawn between the two points. To find the average gradient between any two points on a curve we calculate the gradient of the secant line that passes through both points.
Example 2.1
Find the average gradient of the graph [latex]\scriptsize f(x)={{x}^{2}}-3x-4[/latex] between the points [latex]\scriptsize x=1[/latex] and [latex]\scriptsize x=3[/latex].
Solution
Let’s draw the graph, plot the points and draw the secant between them so we can visualise what is being asked.
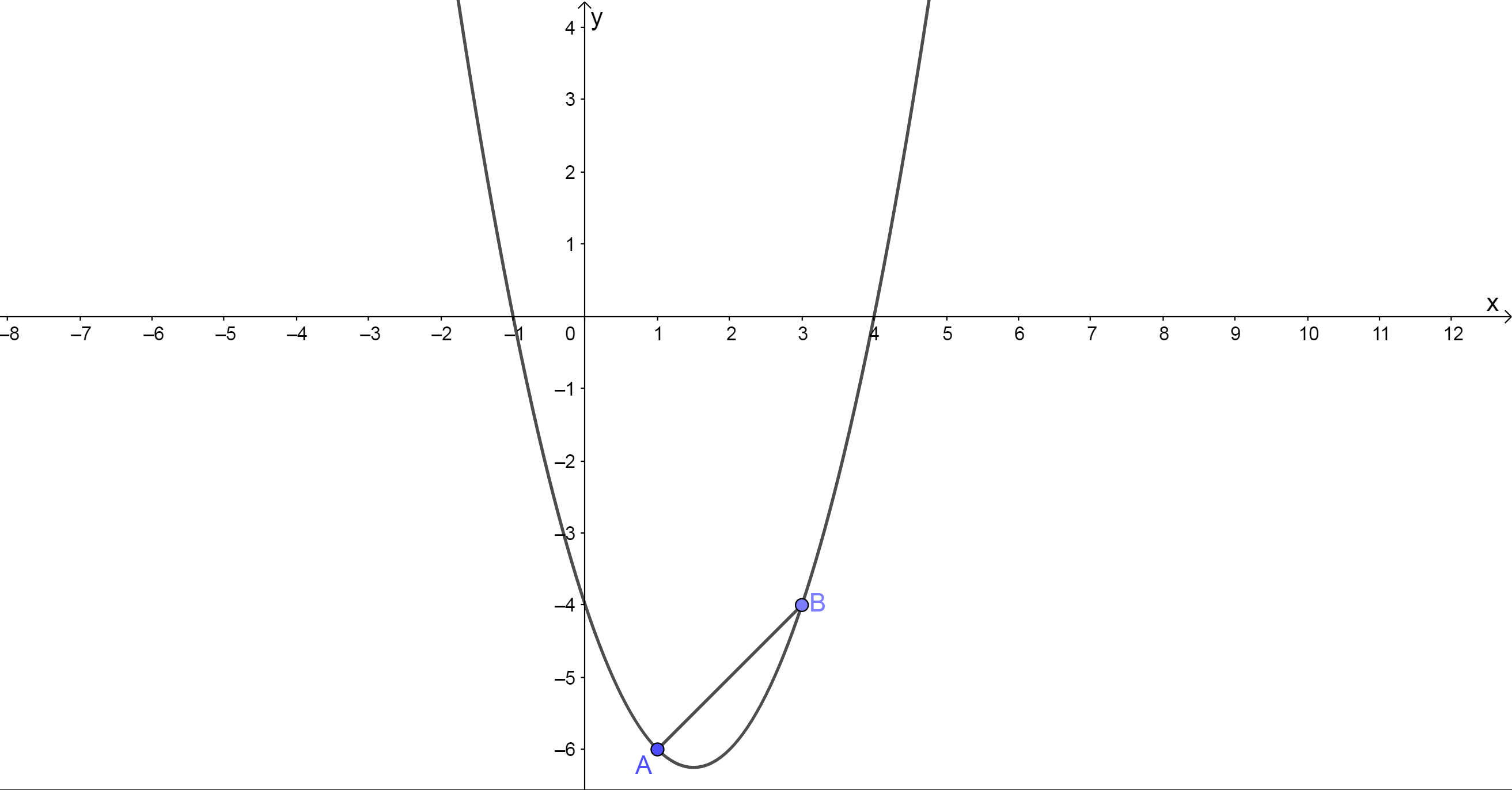
Since we can draw a straight line between the points A and B, we can find the average gradient using the gradient formula.
[latex]\scriptsize {{m}_{{\text{AB}}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex]
To use this formula, we need to find the function values at [latex]\scriptsize x=1[/latex] and [latex]\scriptsize x=3[/latex].
[latex]\scriptsize f(1)={{(1)}^{2}}-3(1)-4=-6[/latex] and [latex]\scriptsize f(3)={{(3)}^{2}}-3(3)-4=-4[/latex]
So we need to find the gradient between the points [latex]\scriptsize (1,-6)[/latex] and [latex]\scriptsize (3,-4)[/latex] to find the gradient of the graph [latex]\scriptsize f(x)={{x}^{2}}-3x-4[/latex] between the points [latex]\scriptsize x=1[/latex] and [latex]\scriptsize x=3[/latex].
[latex]\scriptsize \begin{align*}{{m}_{{\text{AB}}}}&=\displaystyle \frac{{-6-(-4)}}{{1-3}}\\&=\displaystyle \frac{{-2}}{{-2}}\\&=1\end{align*}[/latex]
In Example 2.1 we saw that to calculate the average gradient of a curve we need two points so that we can calculate the gradient of the secant.
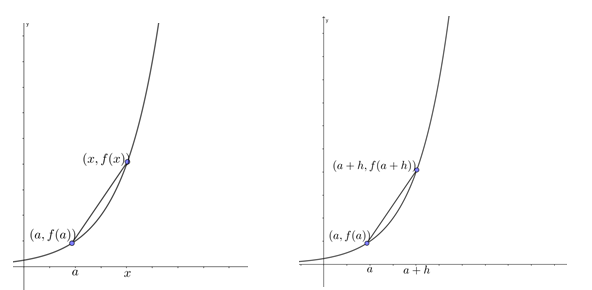
In Figure 2 we can see that we can calculate the slope of a secant line in two ways. [latex]\scriptsize {{m}_{{\sec ant}}}=\displaystyle \frac{{f(x)-f(a)}}{{x-a}}[/latex] or [latex]\scriptsize {{m}_{{\sec ant}}}=\displaystyle \frac{{f(a+h)-f(a)}}{{(a+h)-a}}[/latex].
In the second gradient calculation we find the slope of the secant by replacing [latex]\scriptsize x[/latex] with [latex]\scriptsize a+h[/latex], where [latex]\scriptsize h[/latex] is any distance between the points. We can then calculate the slope of the line through the points [latex]\scriptsize \displaystyle \left( {a,\text{ }f\left( a \right)} \right)[/latex] and [latex]\scriptsize \displaystyle \left( {a\text{ }+\text{ }h,\text{ }f\left( {a\text{ }+\text{ }h} \right)} \right)[/latex]. We simplify the denominator of the second equation for the gradient of the secant to get:
[latex]\scriptsize \begin{align*}{{m}_{{\sec ant}}}&=\displaystyle \frac{{f(a+h)-f(a)}}{{a+h-a}}\\&=\displaystyle \frac{{f(a+h)-f(a)}}{h}\end{align*}[/latex]
But, how do we find the gradient at a specific point on a curve?
To find the gradient at a specific point on a curve, we need calculus.
Activity 2.1: Find the gradient at a point on a curve
Time required: 20 minutes
What you need:
- pen and paper
What to do:
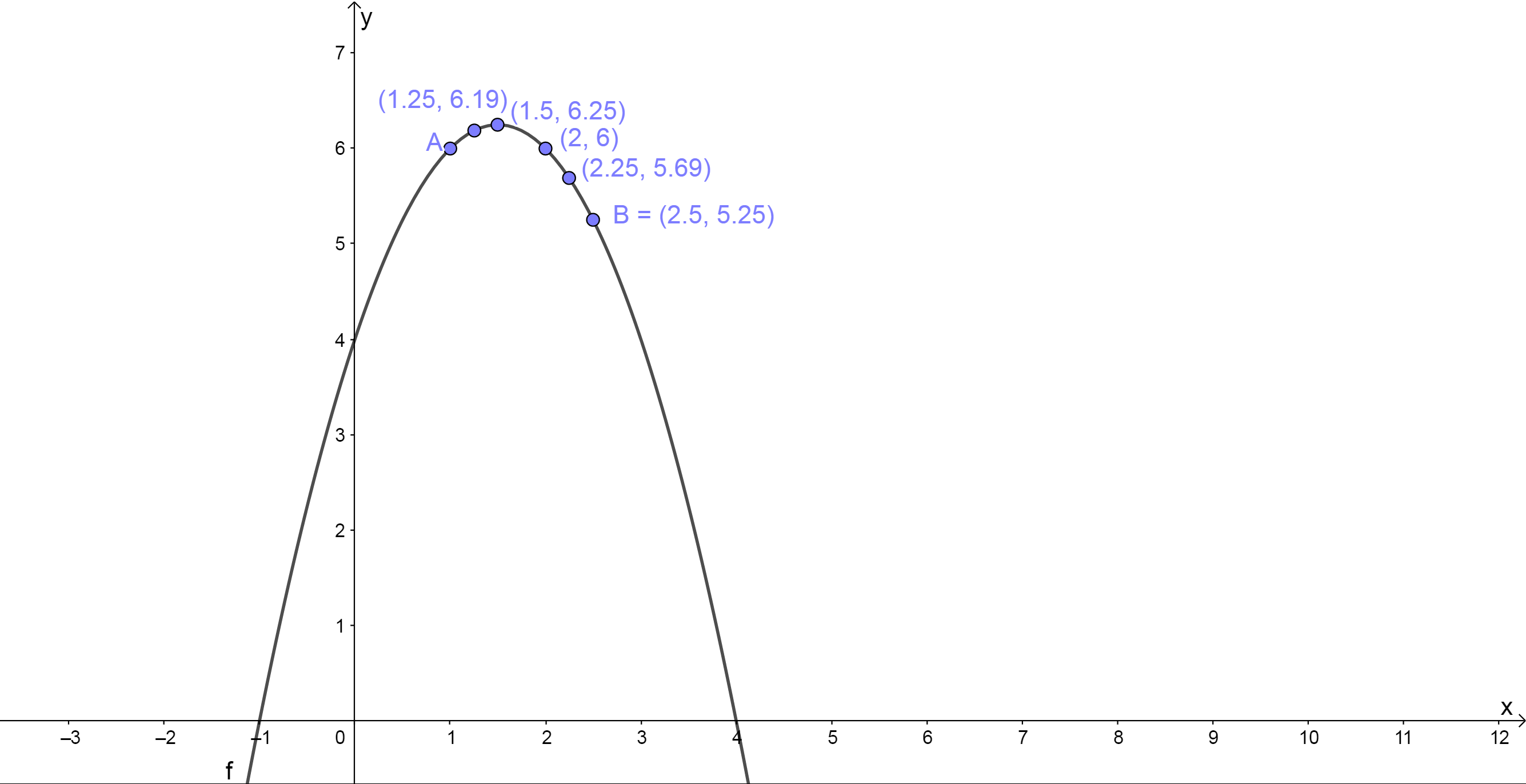
Imagine that there is a point B that moves closer and closer to a fixed point [latex]\scriptsize \text{A}(1,6)[/latex] as shown.
- Find the gradient of the secant between [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize \text{B}(2.5,\text{ }5.25)[/latex].
- Find the gradient of the secant between [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (2.25,\text{ }5.69)[/latex].
- Find the gradient of the secant between [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (2,\text{ 6})[/latex].
- Find the gradient of the secant between [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (1.5,\text{ 6}\text{.25})[/latex].
- Find the gradient of the secant between [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (1.25,\text{ 6}\text{.19})[/latex].
- Let [latex]\scriptsize h[/latex] be the distance between point A and point B. What value does [latex]\scriptsize h[/latex] approach as point B gets closer and closer to point A?
- What happens to the average gradient as B moves towards point A?
- What is the average gradient when B overlaps with A?
- Let A be the point [latex]\scriptsize (a,\text{ }f(a))[/latex] and B be the point [latex]\scriptsize (a+h,\text{ }f(a+h))[/latex], where the distance [latex]\scriptsize h\to 0[/latex] as B moves closer and closer to A. Use your knowledge of limits to write down an expression for the gradient at point A as [latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,[/latex].
What did you find?
For parts 1 to 5 of this question the average gradients between the points are shown in the table below. Notice how the sign of the gradient changes as the point B moves towards A. It starts off as a negative slope then reaches a gradient of zero at the turning point and then the slope becomes positive after the graph turns.
| Points | Average gradient |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (2.5,\text{ }5.25)[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{5.25-6}}{{2.5-1}}\\&=-0.5\end{align*}[/latex] |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (2.25,\text{ }5.68)[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{5.68-6}}{{2.25-1}}\\&=-0.25\end{align*}[/latex] |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (2,\text{ 6})[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{6-6}}{{2-1}}\\&=0\end{align*}[/latex] |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (1.5,\text{ 6}\text{.25})[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{6.25-6}}{{1.5-1}}\\&=0.5\end{align*}[/latex] |
| [latex]\scriptsize \text{A}(1,6)[/latex] and [latex]\scriptsize (1.25,\text{ 6}\text{.19})[/latex] | [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{6.19-6}}{{1.25-1}}\\&=0.76\end{align*}[/latex] |
- The distance [latex]\scriptsize h[/latex] approaches [latex]\scriptsize 0[/latex] as B moves closer and closer to A.
- The gradient of the straight line that passes through points A and B changes as B moves closer to A.
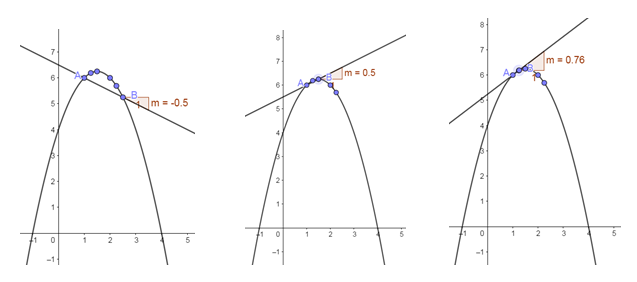
At the point where A and B overlap, the straight line only passes through one point on the curve. This line is known as a tangent to the curve. We can now introduce the idea of the gradient at a single point on a curve. The gradient at a point on a curve is the gradient of the tangent to the curve at the given point. - We see that as point B approaches point A, [latex]\scriptsize h[/latex] gets closer to [latex]\scriptsize 0[/latex]. If point B lies on point A, then [latex]\scriptsize h=0[/latex] and the formula for the average gradient is undefined.
- We use our knowledge of limits to let [latex]\scriptsize h[/latex] tend to [latex]\scriptsize 0[/latex] and determine the gradient of the curve at point A. The gradient at point A as [latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,[/latex] is given by:
[latex]\scriptsize \begin{align*}{{m}_{A}}=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{{a+h-a}}\\=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{h}\end{align*}[/latex]
Activity 2.1 has shown that the gradient at a single point on a curve is the same as the gradient of the tangent to the curve at the given point.
Example 2.2
Given [latex]\scriptsize f(x)=-2{{x}^{2}}[/latex]:
- Determine the average gradient between the points A, where[latex]\scriptsize \displaystyle x=1[/latex], and B, where [latex]\scriptsize \displaystyle x=3[/latex].
- Determine the gradient of the curve at point A.
Solution
- The average gradient between A and B:
[latex]\scriptsize \begin{align*}{{m}_{{AB}}}&=\displaystyle \frac{{f(3)-f(1)}}{{3-1}}\\&=\displaystyle \frac{{-2{{{(3)}}^{2}}-(-2{{{(1)}}^{2}})}}{2}\\&=\displaystyle \frac{{-18+2}}{2}\\&=-8\end{align*}[/latex] - The average gradient between any two points on [latex]\scriptsize f(x)[/latex]:
.
[latex]\scriptsize \displaystyle \frac{{f(a+h)-f(a)}}{{(a+h)-a}}[/latex]
Substitute [latex]\scriptsize (a+h)[/latex] into the given equation [latex]\scriptsize f(x)=-2{{x}^{2}}[/latex] to get a unique expression for the average gradient of this curve.
.
[latex]\scriptsize \begin{align*}\displaystyle \frac{{f(a+h)-f(a)}}{{(a+h)-a}}&=\displaystyle \frac{{-2{{{(a+h)}}^{2}}-{{{(-2a)}}^{2}}}}{h}\\&=\displaystyle \frac{{-2{{a}^{2}}-4ah-2{{h}^{2}}+2{{a}^{2}}}}{h}\\&=\displaystyle \frac{{-4ah-2{{h}^{2}}}}{h}\\&=\displaystyle \frac{{h(-4a-2h)}}{h}\\&=-4a-2h\end{align*}[/latex]
.
Now, to find the gradient at point A we must add in the limit.
.
[latex]\scriptsize {{m}_{A}}=\underset{{h\to 0}}{\mathop{{\lim }}}\,(-4a-2h)[/latex]
.
This is the expression we can use to calculate the gradient at point A.
.
At point A: [latex]\scriptsize \displaystyle x=1[/latex] therefore [latex]\scriptsize a=1[/latex] as this is the point where we want to find the gradient. At a specific point on the curve [latex]\scriptsize h=0[/latex] as shown in Activity 2.1, so the gradient is: [latex]\scriptsize -4(1)-2(0)=-4[/latex].
Exercise 2.1
- Determine the average gradient of the curve [latex]\scriptsize \displaystyle f\left( x \right)=x\left( {x\text{ }+\text{ }3} \right)[/latex] between [latex]\scriptsize \displaystyle x=5[/latex] and [latex]\scriptsize \displaystyle x=3[/latex].
- [latex]\scriptsize \displaystyle \text{A}\left( {1,3} \right)[/latex] is a point on [latex]\scriptsize \displaystyle f\left( x \right)=2{{x}^{2}}-x+1[/latex].
- Determine the gradient of the curve at point A.
- Determine the equation of the tangent line at A.
The full solutions are at the end of the unit.
Differentiation of a function at a point
The type of limit we use to find the slope of the tangent line to a function at a point occurs in many applications across many disciplines. These applications include velocity and acceleration in physics, marginal profit functions in business and growth rates in biology. This limit occurs so frequently that we give it a special name; the derivative.
The process of finding a derivative is called differentiation.
To find the gradient of a tangent to a curve at a point we use the formula: [latex]\scriptsize {f}'(a)=\underset{{x\to a}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x)-f(a)}}{{x-a}}[/latex] or [latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{h}[/latex]. We can use this formula to determine an expression that describes the gradient of the graph (or the gradient of the tangent to the graph) at any point on the graph. This expression (or gradient function) is called the derivative.
The derivative of a function [latex]\scriptsize \displaystyle f\left( x \right)[/latex] is written as [latex]\scriptsize \displaystyle {f}'\left( x \right)[/latex] and is [latex]\scriptsize {f}'(x)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}[/latex].
Activity 2.2: Estimating a derivative
Time required: 10 minutes
What you need:
- pen and paper
What to do:
- For [latex]\scriptsize f(x)={{x}^{3}}[/latex], use [latex]\scriptsize {f}'(a)=\underset{{x\to a}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x)-f(a)}}{{x-a}}[/latex] to write an expression for [latex]\scriptsize {f}'(2)[/latex].
- For [latex]\scriptsize f(x)={{x}^{3}}[/latex], use the table below and the equation you found above to estimate [latex]\scriptsize {f}'(2)[/latex].
[latex]\scriptsize x[/latex] [latex]\scriptsize \displaystyle \frac{{f(x)-f(a)}}{{x-a}}[/latex] [latex]\scriptsize 1.9[/latex] [latex]\scriptsize 1.99[/latex] [latex]\scriptsize 1.999[/latex] [latex]\scriptsize 2.001[/latex] [latex]\scriptsize 2.01[/latex] [latex]\scriptsize 2.1[/latex] - After examining the table, what is a good estimate of [latex]\scriptsize {f}'(2)[/latex] as [latex]\scriptsize x\to 2[/latex]?
- Without using a table, estimate [latex]\scriptsize {f}'(3)[/latex] by using [latex]\scriptsize {f}'(a)=\underset{{x\to a}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x)-f(a)}}{{x-a}}[/latex].
- Now, find [latex]\scriptsize {f}'(3)[/latex] by using [latex]\scriptsize {f}'(x)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}[/latex].
- Compare your answers in questions 4 and 5. What do you notice?
What did you find?
- .
[latex]\scriptsize f(x)={{x}^{3}}[/latex]
[latex]\scriptsize \begin{align*}{f}'(2)=\underset{{x\to 2}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{3}}-{{2}^{3}}}}{{x-2}}\\=\underset{{x\to 2}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{3}}-8}}{{x-2}}\end{align*}[/latex] - .
[latex]\scriptsize x[/latex] [latex]\scriptsize \displaystyle \frac{{f(x)-f(a)}}{{x-a}}[/latex] [latex]\scriptsize 1.9[/latex] [latex]\scriptsize 11.41[/latex] [latex]\scriptsize 1.99[/latex] [latex]\scriptsize 11.9401[/latex] [latex]\scriptsize 1.999[/latex] [latex]\scriptsize 11.994001[/latex] [latex]\scriptsize 2.001[/latex] [latex]\scriptsize 12.006001[/latex] [latex]\scriptsize 2.01[/latex] [latex]\scriptsize 12.0601[/latex] [latex]\scriptsize 2.1[/latex] [latex]\scriptsize 12.61[/latex] - .
After examining the table, we can see that a good estimate for [latex]\scriptsize {f}'(2)[/latex] is [latex]\scriptsize 12[/latex]. - .
[latex]\scriptsize \begin{align*}{f}'(3)=\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{3}}-{{3}^{3}}}}{{x-3}}\\=\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{3}}-27}}{{x-3}}\end{align*}[/latex]
Before we find this limit, here is a quick reminder on how to factorise a difference of cubes.
Step 1: Take the cube root of terms that are perfect cubes
[latex]\scriptsize \sqrt[3]{{{{x}^{3}}}}=x[/latex]
[latex]\scriptsize \sqrt[3]{{27}}=3[/latex]
These give the terms in the first bracket.
[latex]\scriptsize {{x}^{3}}-27=(x-3)(\text{ })[/latex]
Step 2: Find the three terms in the second bracket.
Square the first term from the first bracket to get [latex]\scriptsize {{x}^{2}}[/latex]then square the second term from the first bracket to get [latex]\scriptsize 9[/latex]. Lastly, multiply the first term by the second term in the first bracket and change the sign to get [latex]\scriptsize +3x[/latex].
[latex]\scriptsize {{x}^{3}}-27=(x-3)({{x}^{2}}\text{+}3x+9)[/latex]
.
Simplify and factorise the numerator.
[latex]\scriptsize \displaystyle \underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{3}}-27}}{{x-3}}=\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{(x-3)({{x}^{2}}+3x+9)}}{{x-3}}[/latex]
Cancel the common factor and evaluate the limit.
[latex]\scriptsize \displaystyle \begin{align*}=\underset{{x\to 3}}{\mathop{{\lim }}}\,{{x}^{2}}+3x+9\\=27\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{f}'(3)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(3+h)-f(3)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{{(3+h)}}^{3}}-{{3}^{3}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{27+9{{h}^{2}}+27h+{{h}^{3}}-27}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{9{{h}^{2}}+27h+{{h}^{3}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{h(9h+27+{{h}^{2}})}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,9h+27+{{h}^{2}}\\&=27\end{align*}[/latex] - .
Without using a table, we saw that the results are the same whether we use [latex]\scriptsize {f}'(a)=\underset{{x\to a}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x)-f(a)}}{{x-a}}[/latex] or [latex]\scriptsize {f}'(x)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}[/latex]. [latex]\scriptsize {f}'(3)=27[/latex].
.
The first formula is the definition of the gradient of a tangent line to [latex]\scriptsize f(x)[/latex] passing through the point [latex]\scriptsize (a,f(a))[/latex]. In this case [latex]\scriptsize (3,f(3))[/latex], so the slope of the tangent at the point [latex]\scriptsize x=3[/latex] is [latex]\scriptsize 27[/latex].
.
We have also seen that we may define [latex]\scriptsize {f}'(x)[/latex] passing through the point [latex]\scriptsize (a,f(a))[/latex] as [latex]\scriptsize {f}'(a)=\underset{{x\to a}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x)-f(a)}}{{x-a}}[/latex].
Alternatively, we may also define [latex]\scriptsize {f}'(x)[/latex] at [latex]\scriptsize a[/latex] as [latex]\scriptsize {f}'(a)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{h}[/latex]. So we say the derivative of [latex]\scriptsize f[/latex] at [latex]\scriptsize x=3[/latex] is [latex]\scriptsize 27[/latex].
As we have seen, the derivative of a function at a given point gives us the slope of the tangent line to the function at that point. Knowing the derivative of a function at every point can give valuable information about the behaviour of various functions.
Note
Take a look at this online tool to explore the development of the derivate.
Tick the ‘show tangent’ and ‘show slope value’ boxes and drag the point to explore the gradient.
Differentiation from first principles
We have seen that we use the formula [latex]\scriptsize {f}'(x)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}[/latex] to find the derivative of a function. This method is called differentiation from first principles or using the definition.
There are different notations used to refer to derivatives. If we use the common notation [latex]\scriptsize \displaystyle y=f\left( x \right)[/latex] where the dependent variable is [latex]\scriptsize y[/latex] and the independent variable is [latex]\scriptsize x[/latex], then some alternative notations for the derivative are as follows:
[latex]\scriptsize {f}'(x)={y}'=\displaystyle \frac{{dy}}{{dx}}=\displaystyle \frac{d}{{dx}}[f(x)]=Df(x)={{D}_{x}}y[/latex]
The symbols [latex]\scriptsize D[/latex] and [latex]\scriptsize \displaystyle \frac{d}{{dx}}[/latex] are called differential operators because they tell us that we are differentiating whenever we see them.
[latex]\scriptsize \displaystyle \frac{{dy}}{{dx}}[/latex] is not a fraction! It means [latex]\scriptsize y[/latex] differentiated with respect to [latex]\scriptsize x[/latex]. Similarly, [latex]\scriptsize \displaystyle \frac{{dt}}{{dx}}[/latex] means [latex]\scriptsize t[/latex] differentiated with respect to [latex]\scriptsize x[/latex].
You must learn to identify the different ways of denoting the derivative and be consistent with how you use them.
Example 2.3
- Find the derivative of [latex]\scriptsize f(x)=2{{x}^{2}}-1[/latex] from first principles.
- Calculate [latex]\scriptsize {f}'(2)[/latex] and interpret the answer.
Solutions
- Step 1: Write down the formula for finding the derivative using first principles.
.
[latex]\scriptsize {f}'(x)=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}[/latex]
.
Step 2: Determine [latex]\scriptsize f(x+h)[/latex]
.
[latex]\scriptsize \begin{align*}f(x+h)=2{{(x+h)}^{2}}-1\\=2({{x}^{2}}+2xh+{{h}^{2}})-1\\=2{{x}^{2}}+4xh+2{{h}^{2}}-1\end{align*}[/latex]
.
Step 3: Substitute into the formula and simplify.
.
[latex]\scriptsize \begin{align*}{f}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+4xh+2{{h}^{2}}-1-(2{{x}^{2}}-1)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+4xh+2{{h}^{2}}-1-2{{x}^{2}}+1}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{4xh+2{{h}^{2}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{h(4x+2h)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,4x+2h\\=4x\end{align*}[/latex]
.
Step 4: Write the final answer.
.
[latex]\scriptsize {f}'(x)=4x[/latex] - [latex]\scriptsize {f}'(x)=4x[/latex]
[latex]\scriptsize \begin{align*}{f}'(2)=4(2)\\=8\end{align*}[/latex]- The derivative of [latex]\scriptsize f(x)[/latex] at [latex]\scriptsize \displaystyle x=2[/latex] is [latex]\scriptsize 8[/latex].
- The gradient of the function [latex]\scriptsize f[/latex] at [latex]\scriptsize \displaystyle x=2[/latex] is equal to [latex]\scriptsize 8[/latex].
- The gradient of the tangent to [latex]\scriptsize f(x)[/latex] at [latex]\scriptsize \displaystyle x=2[/latex] is equal to [latex]\scriptsize 8[/latex].
Exercise 2.2
- [latex]\scriptsize g(x)=4x-1[/latex]
- Write down the gradient of [latex]\scriptsize g(x)[/latex].
- Find the derivative of [latex]\scriptsize g(x)[/latex].
- Compare your answers from a) and b). What do you notice?
- Write down [latex]\scriptsize {g}'(-3)[/latex]. Interpret your answer.
- What is the gradient anywhere along [latex]\scriptsize g(x)[/latex]? Why?
- Calculate [latex]\scriptsize \displaystyle \frac{{dk}}{{dx}}[/latex] from first principles if [latex]\scriptsize k(x)=-\displaystyle \frac{2}{x}[/latex].
- Differentiate [latex]\scriptsize f(x)=\displaystyle \frac{1}{2}[/latex] from first principles and interpret the answer.
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- How to define a tangent and secant to a curve.
- How to find the average gradient between two points on a curve.
- How to calculate the gradient of a tangent to a curve at a specific point.
- The definition of a derivative and its relation to the gradient of a tangent to a curve at a single point.
- To differentiate a function by using the formula for first principles.
Unit 2: Assessment
Suggested time to complete: 25 minutes
- Determine the gradient of the tangent to [latex]\scriptsize f(x)=\displaystyle \frac{3}{x}\text{ (}x\ne 0)[/latex] at [latex]\scriptsize x=a[/latex].
- Determine the equation of the tangent to [latex]\scriptsize g(x)={{x}^{2}}+3x[/latex] at [latex]\scriptsize x=-1[/latex].
- Determine [latex]\scriptsize {f}'(x)[/latex] from first principles if [latex]\scriptsize f(x)=-2-3x[/latex].
- If [latex]\scriptsize f(x)=3{{x}^{2}}-3[/latex] determine:
- [latex]\scriptsize {f}'(x)[/latex] from first principles
- [latex]\scriptsize {f}'(2)[/latex].
- What does your answer to [latex]\scriptsize 4 \text{b)}[/latex] represent?
The full solutions are at the end of the unit.
Unit 2: Solutions
Exercise 2.1
- Start by finding the functions values at the given x-values:
[latex]\scriptsize \displaystyle \begin{align*}f\left( 5 \right)&=5\left( {\text{5 }+\text{ }3} \right)\\&=40\end{align*}[/latex] and [latex]\scriptsize \displaystyle \begin{align*}f\left( 3 \right)&=3\left( {\text{3 }+\text{ }3} \right)\\&=18\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{f(3)-f(5)}}{{3-5}}\\&=\displaystyle \frac{{18-40}}{{-2}}\\&=11\end{align*}[/latex] - .
- Gradient at a point on [latex]\scriptsize \displaystyle f\left( x \right)=2{{x}^{2}}-x+1[/latex]:
[latex]\scriptsize \begin{align*}m&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{{a+h-a}}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{h}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}m&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{{a+h-a}}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{{(a+h)}}^{2}}-(a+h)+1-[2{{{(a)}}^{2}}-a+1]}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2({{a}^{2}}+2ah+{{h}^{2}})-a-h+1-2{{a}^{2}}+a-1}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{a}^{2}}+4ah+2{{h}^{2}}-h-2{{a}^{2}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{h(4a+2h-1)}}{h}\\&=4a-1\end{align*}[/latex]
.
At [latex]\scriptsize \displaystyle \text{A}\left( {1,3} \right)[/latex]
[latex]\scriptsize \begin{align*}a&=1\\h&=0\end{align*}[/latex]
[latex]\scriptsize 4(1)-1=3[/latex]
Gradient at [latex]\scriptsize \displaystyle \text{A}\left( {1,3} \right)=3[/latex] - [latex]\scriptsize {{m}_{{\tan }}}=3[/latex]
Equation of the tangent:
We know that [latex]\scriptsize \displaystyle m=\displaystyle \frac{{\text{change in }y}}{{\text{change in }x}}[/latex]
By re-arranging the formulae we get:
[latex]\scriptsize \begin{align*}y-{{y}_{1}}&=m(x-{{x}_{1}})\\y-3&=3(x-1)\\y&=3x-3+3\\y&=3x\end{align*}[/latex]
- Gradient at a point on [latex]\scriptsize \displaystyle f\left( x \right)=2{{x}^{2}}-x+1[/latex]:
Exercise 2.2
- [latex]\scriptsize g(x)=4x-1[/latex]
- The gradient of the straight line [latex]\scriptsize g(x)[/latex] is [latex]\scriptsize 4[/latex].
- .
[latex]\scriptsize \begin{align*}{g}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{g(x+h)-g(x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{4(x+h)-1-(4x-1)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{4x+4h-1-4x+1}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{4h}}{h}\\&=4\end{align*}[/latex] - The answers to a and b are the same. The derivate of a function is equivalent to finding the gradient or slope of the function.
- [latex]\scriptsize {g}'(-3)=4[/latex] tells us that the slope of the graph at [latex]\scriptsize x=-3[/latex] is [latex]\scriptsize 4[/latex].
- The gradient anywhere along [latex]\scriptsize g(x)=4[/latex] because [latex]\scriptsize g(x)=4x-1[/latex] is a straight line. The gradient anywhere along a straight line is constant.
- .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{dk}}{{dx}}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{k(x+h)-k(x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-\displaystyle \frac{2}{{(x+h)}}-\left( {\displaystyle \frac{{-2}}{x}} \right)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-\displaystyle \frac{2}{{(x+h)}}+\displaystyle \frac{2}{x}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\displaystyle \frac{{-2(x)+2(x+h)}}{{x(x+h)}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-2x+2x+2h}}{{x(x+h)h}}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2h}}{{x(x+h)h}}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{2}{{x(x+h)}}\\&=\displaystyle \frac{2}{{{{x}^{2}}}}\end{align*}[/latex]
Notice: even though [latex]\scriptsize h[/latex] remains in the denominator, we can take the limit since it does not result in division by [latex]\scriptsize 0[/latex]. - .
[latex]\scriptsize \begin{align*}{f}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\tfrac{1}{2}-\tfrac{1}{2}}}{h}\\&=0\end{align*}[/latex]
The gradient of [latex]\scriptsize f(x)=\displaystyle \frac{1}{2}[/latex] is [latex]\scriptsize 0[/latex] at any point on the graph. The slope of a constant function (graph parallel to the x-axis) is always equal to [latex]\scriptsize 0[/latex].
Unit 2: Assessment
- Gradient of tangent at [latex]\scriptsize x=a[/latex]:
[latex]\scriptsize \displaystyle \begin{align*}m&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(a+h)-f(a)}}{{a+h-a}}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{\displaystyle \frac{3}{{(a+h)}}-\displaystyle \frac{3}{a}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{1}{h}\times \left( {\displaystyle \frac{3}{{(a+h)}}-\displaystyle \frac{3}{a}} \right)\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{1}{h}\left( {\displaystyle \frac{{3a-3(a+h)}}{{a(a+h)}}} \right)\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\left( {\displaystyle \frac{{3a-3a-3h}}{{ah(a+h)}}} \right)\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\left( {\displaystyle \frac{{-3h}}{{ah(a+h)}}} \right)\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\left( {\displaystyle \frac{{-3}}{{a(a+h)}}} \right)\\&=\displaystyle \frac{{-3}}{{{{a}^{2}}}}\end{align*}[/latex] - Gradient of [latex]\scriptsize g(x)={{x}^{2}}+3x[/latex] is given by:
[latex]\scriptsize \displaystyle \begin{align*}{g}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{g(x+h)-g(x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{{(x+h)}}^{2}}+3(x+h)-({{x}^{2}}+3x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{2}}+2xh+{{h}^{2}}+3x+3h-{{x}^{2}}-3x}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2xh+{{h}^{2}}+3h}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{h(2x+h+3)}}{h}\\&=2x+3\end{align*}[/latex]
Gradient of tangent at [latex]\scriptsize x=-1[/latex]:
Substitute the x-value into the general form of the gradient expression:
[latex]\scriptsize \begin{align*}{g}'(-1)&=2(-1)+3\\&=-2+3\\&=1\end{align*}[/latex] - Therefore, the gradient of tangent at [latex]\scriptsize x=-1[/latex] is [latex]\scriptsize 1[/latex].
[latex]\scriptsize \begin{align*}{f}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-2-3(x+h)-(-2-3x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-2-3x-3h+2+3x}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{-3h}}{h}\\&=-3\end{align*}[/latex] - .
- .
[latex]\scriptsize \displaystyle \begin{align*}{f}'(x)&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{f(x+h)-f(x)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{3{{{(x+h)}}^{2}}-3-(3{{x}^{2}}-3)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{3{{x}^{2}}+6xh+{{h}^{2}}-3-3{{x}^{2}}+3}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{6xh+{{h}^{2}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{h(6x+h)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,6x+h\\&=6x\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{f}'(2)&=6(2)\\&=12\end{align*}[/latex] - .
The gradient of the curve [latex]\scriptsize f(x)=3{{x}^{2}}-3[/latex] at [latex]\scriptsize x=2[/latex] is [latex]\scriptsize 12[/latex].
OR
The gradient of the tangent to curve [latex]\scriptsize f(x)=3{{x}^{2}}-3[/latex] at [latex]\scriptsize x=2[/latex] is [latex]\scriptsize 12[/latex].
- .
Media Attributions
- Img 01_Newton and Leibniz © Wikimedia is licensed under a CC BY (Attribution) license
- Img02_Example 2.1 average gradient © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- Fig01_both secants in one figure © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- Fig 02_how do you find gradient at a point © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- Fig 03Activity_gradient at a point © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- Fig 5_Activity_gradient as A gets closer to B © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
A line that intersects two or more points on a curve.