Functions and algebra: Use a variety of techniques to sketch and interpret information from graphs of functions
Unit 1: Sketch quadratic functions
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Sketch quadratic functions of the form [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex] and [latex]\scriptsize \displaystyle y=a{{(x+p)}^{2}}+q[/latex].
- Find the turning point of [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex] and [latex]\scriptsize \displaystyle y=a{{(x+p)}^{2}}+q[/latex].
What you should know
Before you start this unit, make sure you can:
- Solve quadratic equations by:
- Factorisation
- Completing the square
- Using the quadratic formula.
- Plot quadratic functions of the form [latex]\scriptsize y=a{{x}^{2}}+q[/latex].
- Determine the x- and y-intercepts of a quadratic function.
- Determine the domain and range of a quadratic function.
- Determine the turning point (TP) of a quadratic function of the form [latex]\scriptsize y=a{{x}^{2}}+q[/latex].
Review unit 1 of subject outcome 2.3 for level 2 and unit 1, unit 2 and unit 3 of subject outcome 2.3 for level 3 for help with solving quadratic functions. Review unit 2 of subject outcome 2.1 for level 2 for help with plotting quadratic functions of the form [latex]\scriptsize y=a{{x}^{2}}+q[/latex].
Introduction
In level 2 we were introduced to the quadratic function of the form [latex]\scriptsize y=a{{x}^{2}}+q[/latex]. We learnt that quadratic functions were useful in real life for modelling the flights of objects through the air, designing bridges and describing the shapes of objects such as satellite dishes.
Before we go on with this unit, let’s briefly revise what we know about quadratic functions of the form [latex]\scriptsize y=a{{x}^{2}}+q[/latex].
Take note!
- The function of the form [latex]\scriptsize y=a{{x}^{2}}+q[/latex] is a parabola with an axis of symmetry on the y-axis (or the line [latex]\scriptsize x=0[/latex]) and a y-intercept of [latex]\scriptsize (0,q)[/latex].
- Because the axis of symmetry is the line [latex]\scriptsize x=0[/latex], the turning point (TP) and the y-intercept are the same point, therefore, the TP is the point [latex]\scriptsize (0,q)[/latex].
- If [latex]\scriptsize a \gt 0[/latex] the graph curves upwards and has a minimum TP.
- If [latex]\scriptsize a \lt 0[/latex] the graph curves downwards and has a maximum TP.
- If [latex]\scriptsize a \gt 0[/latex] and [latex]\scriptsize q \gt 0[/latex] or if [latex]\scriptsize a \lt 0[/latex] and [latex]\scriptsize q \lt 0[/latex] the graph has no x-intercepts and the equation has no real roots.
- If [latex]\scriptsize q=0[/latex] the graph touches the origin – the point where the x-axis and y-axis intersect, and the equation has one real root.
This is all illustrated in Figure 1.

The turning point form
We know that [latex]\scriptsize a[/latex] affects the shape of the parabola and whether it is concave up (a ‘smile’) or concave down (a ‘frown’) and that [latex]\scriptsize q[/latex] shifts the parabola vertically up or down. But in all cases, the graph is symmetrical about the y-axis (or the line [latex]\scriptsize x=0[/latex]).
Now let’s look at how to shift the graph horizontally left or right.
Activity 1.1: Find the turning points of the function y = a(x + p)2 + q
Time required: 15 minutes
What you need:
- paper
- pen or pencil
What to do:
- Make a copy of the following table on a blank piece of paper and then complete it by finding the y-values for each of the x-values for each function. Each function is of the form [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex].
x-values [latex]\scriptsize -3[/latex] [latex]\scriptsize -2[/latex] [latex]\scriptsize -1[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 1[/latex] [latex]\scriptsize 2[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize f(x)={{(x-2)}^{2}}[/latex] [latex]\scriptsize g(x)=\displaystyle \frac{1}{2}{{(x+1)}^{2}}[/latex] [latex]\scriptsize h(x)=-{{(x+2)}^{2}}+9[/latex] - Plot each of these functions on the same set of axes.
- What is the axis of symmetry of each function and how does this compare to the value of [latex]\scriptsize p[/latex] in each case?
- What is the turning point of each function and how does this compare to the values of [latex]\scriptsize p[/latex] and [latex]\scriptsize q[/latex] in each function?
- Does the value of [latex]\scriptsize a[/latex] affect the shape of the function of the form [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] in the same way as the function of the form [latex]\scriptsize y=a{{x}^{2}}+q[/latex]?
- How does the value of [latex]\scriptsize a[/latex] affect whether the function has a minimum or maximum turning point?
- Based on what you have discovered, what will the turning point of the following functions be, and will it be a minimum or maximum turning point?
- [latex]\scriptsize b(x)=-{{(x+3)}^{2}}+1[/latex]
- [latex]\scriptsize c(x)=2{{(x-1.5)}^{2}}-\displaystyle \frac{{17}}{4}[/latex]
- [latex]\scriptsize d(x)=-\displaystyle \frac{1}{3}{{(x+r)}^{2}}+s[/latex]
What did you find?
- Here is the completed table of values.
x-values [latex]\scriptsize -3[/latex] [latex]\scriptsize -2[/latex] [latex]\scriptsize -1[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 1[/latex] [latex]\scriptsize 2[/latex] [latex]\scriptsize 3[/latex] [latex]\scriptsize f(x)={{(x-2)}^{2}}[/latex] [latex]\scriptsize 25[/latex] [latex]\scriptsize 16[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 4[/latex] [latex]\scriptsize 1[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize 1[/latex] [latex]\scriptsize g(x)=\displaystyle \frac{1}{2}{{(x+1)}^{2}}[/latex] [latex]\scriptsize 2[/latex] [latex]\scriptsize \displaystyle \frac{1}{2}[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize \displaystyle \frac{1}{2}[/latex] [latex]\scriptsize \displaystyle 2[/latex] [latex]\scriptsize 4.5[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize h(x)=-{{(x+2)}^{2}}+9[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 9[/latex] [latex]\scriptsize 8[/latex] [latex]\scriptsize 5[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -7[/latex] [latex]\scriptsize -16[/latex] - Figure 2 shows all three functions plotted on the same system of axes.
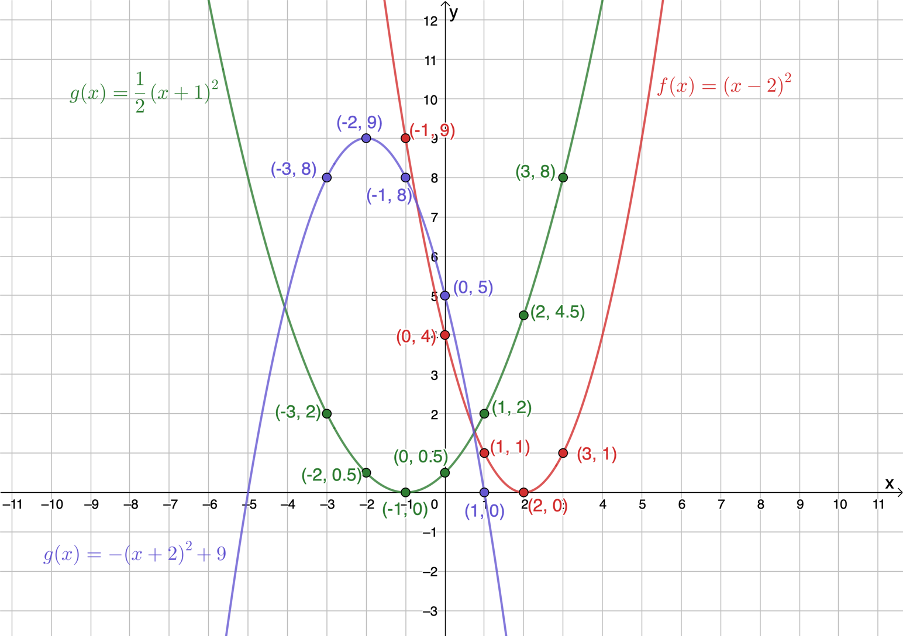
Figure 2: Plots of [latex]\scriptsize f(x)[/latex], [latex]\scriptsize g(x)[/latex] and [latex]\scriptsize h(x)[/latex] - The axis of symmetry of [latex]\scriptsize f(x)[/latex], [latex]\scriptsize g(x)[/latex] and [latex]\scriptsize h(x)[/latex] are [latex]\scriptsize x=2[/latex], [latex]\scriptsize x=-1[/latex] and [latex]\scriptsize x=-2[/latex] respectively. In each case, the axis of symmetry is the value of [latex]\scriptsize p[/latex] multiplied by [latex]\scriptsize -1[/latex], in other words [latex]\scriptsize -p[/latex].
- The turning points of [latex]\scriptsize f(x)[/latex], [latex]\scriptsize g(x)[/latex] and [latex]\scriptsize h(x)[/latex] are [latex]\scriptsize (2,0)[/latex], [latex]\scriptsize (-1,0)[/latex] and [latex]\scriptsize (-2,9)[/latex] respectively. In each case, the coordinates of the turning point are given by [latex]\scriptsize (-p,q)[/latex].
- The value of [latex]\scriptsize a[/latex] has the same effect in [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] as it does in [latex]\scriptsize y=a{{x}^{2}}+q[/latex]. [latex]\scriptsize a \gt 0[/latex] results in a concave up (‘smiley’) graph while [latex]\scriptsize a \lt 0[/latex] results in a concave down graph. The greater the value of [latex]\scriptsize a[/latex] the narrower the graph. The smaller the value of [latex]\scriptsize a[/latex] the wider the graph.
- If [latex]\scriptsize a \gt 0[/latex], the graph has a minimum turning point. If [latex]\scriptsize a \lt 0[/latex], the graph has a maximum turning point.
- We have discovered that a quadratic function of the form [latex]\scriptsize y={{(x+p)}^{2}}+q[/latex] has a turning point of [latex]\scriptsize (-p,q)[/latex]. Therefore, the turning point of
- [latex]\scriptsize b(x)=-{{(x+3)}^{2}}+1[/latex] is [latex]\scriptsize (-3,1)[/latex] and it will be a maximum.
- [latex]\scriptsize c(x)=3{{(x-1.5)}^{2}}-\displaystyle \frac{{17}}{4}[/latex] is [latex]\scriptsize \left( {1.5,-\displaystyle \frac{{17}}{4}} \right)[/latex] and it will be a minimum.
- [latex]\scriptsize d(x)=-\displaystyle \frac{1}{3}{{(x+r)}^{2}}+s[/latex] is [latex]\scriptsize (-r,s)[/latex] and it will be a maximum.
In Activity 1.1 we discovered that the turning point (TP) of the quadratic function of the form [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] is the point [latex]\scriptsize (-p,q)[/latex]. We call this form of the quadratic function the turning point form because we can read the TP directly from the function. Because the x-coordinate of the TP is always the same as the axis of symmetry (A/S), we know that the A/S is the line [latex]\scriptsize x=-p[/latex].
[latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] is the turning point form of the quadratic function and has a TP of [latex]\scriptsize (-p,q)[/latex] and an axis of symmetry of [latex]\scriptsize x=-p[/latex].
If [latex]\scriptsize a \gt 0[/latex], the TP will be a minimum. If [latex]\scriptsize a \lt0[/latex], the TP will be a maximum.
Example 1.1
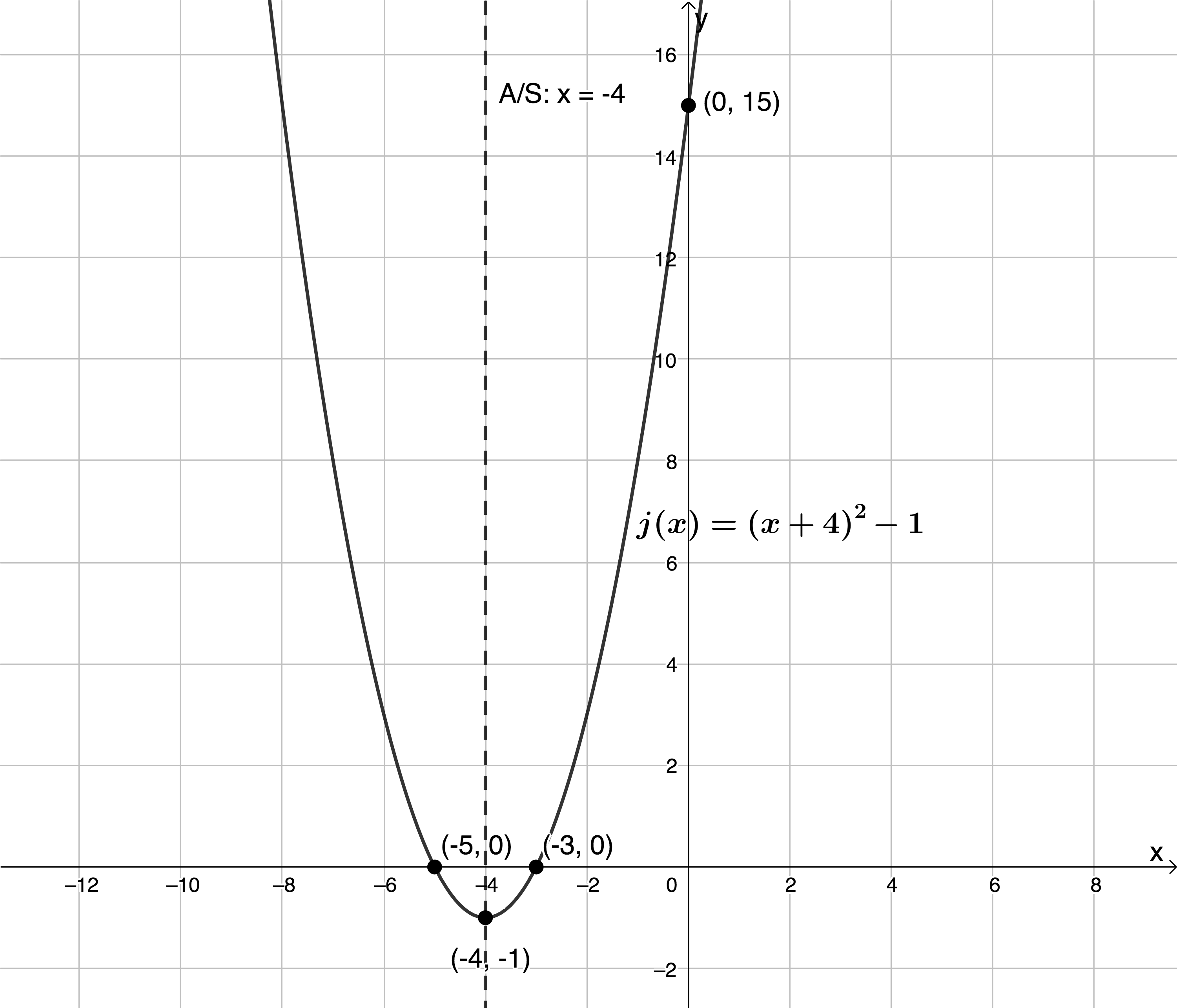
[latex]\scriptsize j(x)={{(x-4)}^{2}}-1[/latex].
- Determine the:
- x-intercepts
- y-intercept
- TP
- A/S
- Domain
- Range
- Make a neat sketch of [latex]\scriptsize j(x)[/latex].
Solutions
- .
- x-intercepts: Let [latex]\scriptsize j(x)=0[/latex]
[latex]\scriptsize \displaystyle \begin{align*}0 & ={{(x-4)}^{2}}-1\\\therefore {{x}^{2}}-8x+16-1 & =0\\\therefore {{x}^{2}}-8x+15 & =0\\\therefore (x-5)(x-3) & =0\\\therefore x=5\text{ } & \text{or }x=3\end{align*}[/latex] - y-intercept: Let [latex]\scriptsize x=0[/latex]
[latex]\scriptsize \begin{align*}j(0)&={{(0-4)}^{2}}-1\\\therefore j(0)&=15\end{align*}[/latex] - The TP is the point [latex]\scriptsize (-p,q)[/latex]. Therefore, the TP is [latex]\scriptsize \left( {-(-4),-1} \right)=(4,-1)[/latex].
- The A/S is the line [latex]\scriptsize x=-p[/latex]. Therefore, the A/S is [latex]\scriptsize x=4[/latex].
- The domain is [latex]\scriptsize \{x:x\in \mathbb{R}\}[/latex] because there is no value of [latex]\scriptsize x[/latex] for which [latex]\scriptsize j(x)[/latex] is undefined.
- We know already that, because [latex]\scriptsize a \gt 0[/latex], the function has a minimum TP. We also know that the TP is the point [latex]\scriptsize (4,-1)[/latex]. Therefore, we know that the range is [latex]\scriptsize \{j(x):j(x)\ge -1\}[/latex] or [latex]\scriptsize [-1,\infty )[/latex] because the TP represents the minimum function value.
.
We can also determine the range by setting up and solving an inequality.[latex]\scriptsize \begin{align*}{{(x-4)}^{2}} & \ge 0 && \text{Any term squared must be greater than zero}\\ \therefore {{(x-4)}^{2}}-1 & \ge -1 && \text{We add }-1\text{ to both sides of the inequality to create the function }\\ &&&j(x)\text{ on one side}\\ \therefore j(x) & \ge -1 && \text{We can replace the LHS with }j(x)\text{ and read the range}\end{align*}[/latex]
- x-intercepts: Let [latex]\scriptsize j(x)=0[/latex]
- Sketch of [latex]\scriptsize j(x)[/latex].
Take note!
In order to sketch functions of the form [latex]\scriptsize \displaystyle y=a{{(x+p)}^{2}}+q[/latex], we need to determine five key characteristics of the graph, as follows:
- the sign of [latex]\scriptsize a[/latex]: this will help us determine if the TP is a maximum or a minimum
- the turning point: remember, we can read the TP directly from this form of the function as [latex]\scriptsize (-p,q)[/latex]
- the axis of symmetry: remember this is the vertical line [latex]\scriptsize x=-p[/latex]
- the y-intercept
- the x-intercepts (if they exist).
Exercise 1.1
- [latex]\scriptsize q(x)=4{{(x-3)}^{2}}-1[/latex]
- [latex]\scriptsize r(x)=-{{(x-5)}^{2}}+4[/latex].
Sketch both functions on the same set of axes by first determining the following for each:- x-intercepts
- y-intercept
- TP
- A/S
- domain
- range.
Mark the intercepts, TP and A/S on your sketch.
The full solutions are at the end of the unit.
Completing the square
From our work on solving quadratic equations, we know that the standard form of the quadratic function is [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex]. In fact, in the section above on the turning point form, we expanded the turning point form to get the equation into the standard form in order to find the x-intercepts by factorising.
If we can convert the standard form into the turning point form, we would have a useful way of finding the TP and A/S of a quadratic function. We can do this by using a process called completing the square. You learnt how to complete the square in unit 2 of subject outcome 2.3 in level 3. If you need more help with completing the square, you should review that unit.
We can expand [latex]\scriptsize y=2{{(x+3)}^{2}}-1[/latex] into standard form to get [latex]\scriptsize y=2{{x}^{2}}+12x+17[/latex]. Check that you can do the expansion and get the same result.
Now we need to find a way to get back to the original equation.
Step 1: We know that we need the coefficient of [latex]\scriptsize x[/latex] inside the square brackets to be [latex]\scriptsize 1[/latex]. So, take out a common factor of [latex]\scriptsize 2[/latex] from each term.
[latex]\scriptsize y=2\left( {{{x}^{2}}+6x+\displaystyle \frac{{17}}{2}} \right)[/latex]
Step 2: We know that the [latex]\scriptsize 6x[/latex] term was the result of [latex]\scriptsize 3x+3x[/latex]. So, divide the coefficient of the [latex]\scriptsize x[/latex] term by [latex]\scriptsize 2[/latex] and then square it to get [latex]\scriptsize 9[/latex]. To keep the expression balanced, we need to add [latex]\scriptsize 9[/latex] to and subtract [latex]\scriptsize 9[/latex] from the right-hand side.
[latex]\scriptsize y=2\left( {{{x}^{2}}+6x+9-9+\displaystyle \frac{{17}}{2}} \right)[/latex]
Step 3: Now the [latex]\scriptsize {{x}^{2}}+6x+9[/latex] part of the right-hand side can be factorised to [latex]\scriptsize {{(x+3)}^{2}}[/latex] which is what we want. But remember, the whole right-hand side is being multiplied by [latex]\scriptsize 2[/latex]. When we take the [latex]\scriptsize -9[/latex] and the [latex]\scriptsize \displaystyle \frac{{17}}{2}[/latex] out of the bracket we have to multiply them by [latex]\scriptsize 2[/latex].
[latex]\scriptsize y=2{{(x+3)}^{2}}-18+17[/latex]
Step 4: Finally, we can simplify to get back to our original equation.
[latex]\scriptsize y=2{{(x+3)}^{2}}-1[/latex]
We can use this process of completing the square to convert any quadratic function in standard form into turning point form.
Example 1.2
Determine the TP and A/S of [latex]\scriptsize t(x)=2-10x+5{{x}^{2}}[/latex] by completing the square to get the function into the turning point form.
Solution
The first thing we need to do is to write [latex]\scriptsize t(x)[/latex] in standard form.
[latex]\scriptsize t(x)=5{{x}^{2}}-10x+2[/latex]
Now we need to take out a common factor of [latex]\scriptsize 5[/latex] so that the cooefficient of [latex]\scriptsize {{x}^{2}}[/latex]is [latex]\scriptsize 1[/latex].
[latex]\scriptsize t(x)=5\left( {{{x}^{2}}-2x+\displaystyle \frac{2}{5}} \right)[/latex]
Next, we have to halve the coefficient of [latex]\scriptsize x[/latex] and then square it. Add and subtract the result from the right-hand side.
[latex]\scriptsize t(x)=5\left( {{{x}^{2}}-2x+1-1+\displaystyle \frac{2}{5}} \right)[/latex]
The [latex]\scriptsize {{x}^{2}}-2x+1[/latex] can be factorised into a perfect square. Remember that the other terms must be multiplied by [latex]\scriptsize 5[/latex].
[latex]\scriptsize t(x)=5{{(x-1)}^{2}}-5+2[/latex]
Now simplify.
[latex]\scriptsize t(x)=5{{(x-1)}^{2}}-3[/latex]
It is always a good idea to check yourself by expanding to see if you get back to the original expression.
[latex]\scriptsize \begin{align*}t(x) & =5{{(x-1)}^{2}}-3\\ & =5({{x}^{2}}-2x+1)-3\\ & =5{{x}^{2}}-10x+5-3\\ & =5{{x}^{2}}-10x+2\end{align*}[/latex]
We get back to the original expression, so we know that we have completed the square correctly.
Now if [latex]\scriptsize t(x)=5{{(x-1)}^{2}}-3[/latex], then the TP is [latex]\scriptsize (1,-3)[/latex] and the A/S is the line [latex]\scriptsize x=1[/latex].
Exercise 1.2
Change [latex]\scriptsize y=-2{{x}^{2}}+3x-4[/latex] into the turning point form by completing the square.
The full solutions are at the end of the unit.
Activity 1.2: Derive a general result for the TP from the standard form of a quadratic equation
Time required: 15 minutes
- What you need:
- a piece of paper
- a pen or pencil
What to do:
- Get [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex] into the turning point form by completing the square.
- What is the x-coordinate of the TP?
- What is the axis of symmetry?
- What is the y-coordinate of the TP?
What did you find?
- The first thing we have to do is take out the common factor [latex]\scriptsize a[/latex].[latex]\scriptsize y=a\left( {{{x}^{2}}+\displaystyle \frac{b}{a}x+\displaystyle \frac{c}{a}} \right)[/latex]
Now we need to halve the [latex]\scriptsize x[/latex] coefficient and square it and then add it and subtract it.
[latex]\scriptsize \begin{align*}y & =a\left( {{{x}^{2}}+\displaystyle \frac{b}{a}x+{{{\left( {\displaystyle \frac{b}{{2a}}} \right)}}^{2}}-{{{\left( {\displaystyle \frac{b}{{2a}}} \right)}}^{2}}+\displaystyle \frac{c}{a}} \right)\\ & =a\left( {{{x}^{2}}+\displaystyle \frac{b}{a}x+\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}-\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}+\displaystyle \frac{c}{a}} \right)\end{align*}[/latex]Now [latex]\scriptsize {{x}^{2}}+\displaystyle \frac{b}{a}x+\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}[/latex] can be factorised as a perfect square.
[latex]\scriptsize y=a{{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}}-a\left( {\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}} \right)+a\left( {\displaystyle \frac{c}{a}} \right)[/latex]
Lastly, we need to simplify.
[latex]\scriptsize \begin{align*}y & =a{{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}}-a\left( {\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}} \right)+a\left( {\displaystyle \frac{c}{a}} \right)\\ & =a{{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}}-\displaystyle \frac{{a{{b}^{2}}}}{{4{{a}^{2}}}}+\displaystyle \frac{{ac}}{a}\\ & =a{{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}}-\displaystyle \frac{{{{b}^{2}}}}{{4a}}+c\\ & =a{{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}}-\displaystyle \frac{{{{b}^{2}}+4ac}}{{4a}}\end{align*}[/latex]
- From the TP form, which we found by completing the square, we can see that the x-coordinate of the TP is given by [latex]\scriptsize -\displaystyle \frac{b}{{2a}}[/latex].
- This means that the A/S is the line [latex]\scriptsize x=-\displaystyle \frac{b}{{2a}}[/latex].
- The y-coordinate of the TP is given by [latex]\scriptsize -\displaystyle \frac{{{{b}^{2}}-4ac}}{{4a}}[/latex].
The TP of [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex] is [latex]\scriptsize \left( {-\displaystyle \frac{b}{{2a}},-\displaystyle \frac{{{{b}^{2}}-4ac}}{{4a}}} \right)[/latex].
The A/S of [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex] is the line [latex]\scriptsize x=-\displaystyle \frac{b}{{2a}}[/latex].
Example 1.3
Determine the TP of [latex]\scriptsize f(x)={{x}^{2}}-6x+8[/latex] and [latex]\scriptsize g(x)=18+6x-3{{x}^{2}}[/latex] without changing the functions into the turning point form.
Solution
For [latex]\scriptsize f(x)={{x}^{2}}-6x+8[/latex], [latex]\scriptsize a=1[/latex], [latex]\scriptsize b=-6[/latex] and [latex]\scriptsize c=8[/latex].
The x-coordinate of the TP is given by [latex]\scriptsize -\displaystyle \frac{b}{{2a}}=-\displaystyle \frac{{(-6)}}{{2(1)}}=3[/latex].
The y-coordinate of the TP is given by [latex]\scriptsize -\displaystyle \frac{{{{b}^{2}}-4ac}}{{4a}}=-\displaystyle \frac{{{{{(-6)}}^{2}}-4(1)(8)}}{{4(1)}}=-\displaystyle \frac{{36-32}}{4}=-\displaystyle \frac{4}{4}=-1[/latex].
We can also find the y-coordinate of the TP by finding the function value of the x-coordinate.
[latex]\scriptsize f(3)={{3}^{2}}-6(3)+8=9-18+8=-1[/latex].
For [latex]\scriptsize g(x)=18+6x-3{{x}^{2}}[/latex], [latex]\scriptsize a=-3[/latex], [latex]\scriptsize b=6[/latex] and [latex]\scriptsize c=18[/latex].
The x-coordinate of the TP is given by [latex]\scriptsize -\displaystyle \frac{b}{{2a}}=-\displaystyle \frac{6}{{2(-3)}}=1[/latex].
The y-coordinate of the TP is given by [latex]\scriptsize -\displaystyle \frac{{{{b}^{2}}-4ac}}{{4a}}=-\displaystyle \frac{{{{6}^{2}}-4(-3)(18)}}{{4(-3)}}=-\displaystyle \frac{{36+216}}{{-12}}=-\displaystyle \frac{{252}}{{-12}}=21[/latex].
We can also find the y-coordinate of the TP by finding the function value of the x-coordinate.
[latex]\scriptsize g(1)=18+6(1)-3{{(1)}^{2}}=18+6-3=21[/latex].
Sketching quadratic functions in standard form
We can now sketch the graphs of quadratic functions of the form [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex] using a number of different methods.
We find the x-intercepts (if they exist) by setting the function equal to zero. We find the y-intercept by setting [latex]\scriptsize x[/latex] equal to zero. However, this means that we can read the y-intercept directly from the standard form. In [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex], the y-intercept is [latex]\scriptsize c[/latex] because if we substitute [latex]\scriptsize x=0[/latex] both the [latex]\scriptsize a{{x}^{2}}[/latex] and [latex]\scriptsize bx[/latex] terms will equal zero.
We can find the TP either by changing the function into the TP form by completing the square or by using the fact that the TP is the point [latex]\scriptsize \left( {-\displaystyle \frac{b}{{2a}},-\displaystyle \frac{{{{b}^{2}}-4ac}}{{4a}}} \right)[/latex]. Remember you can also find the y-coordinate of the TP by finding the function value of the x-coordinate of the TP, in other words, by finding [latex]\scriptsize f\left( {-\displaystyle \frac{b}{{2a}}} \right)[/latex].
Example 1.4
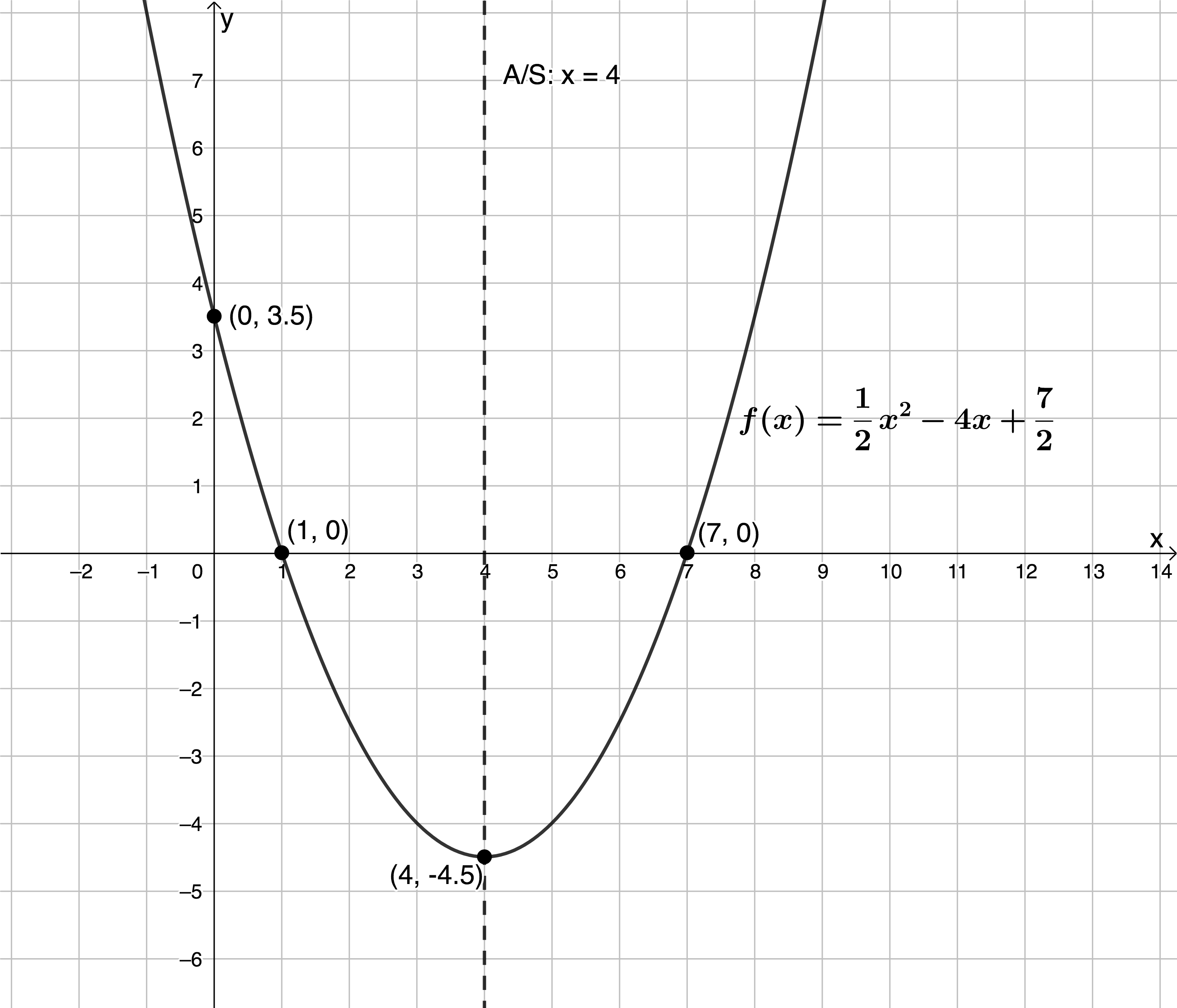
Sketch [latex]\scriptsize f(x)=\displaystyle \frac{1}{2}{{x}^{2}}-4x+\displaystyle \frac{7}{2}[/latex].
Solution
Remember that to sketch a quadratic function we need to determine the intercepts, the TP and the A/S. We also need to determine whether the TP is a maximum or minimum.
x-intercepts: Let [latex]\scriptsize f(x)=0[/latex]
[latex]\scriptsize \displaystyle \begin{align*}\displaystyle \frac{1}{2}{{x}^{2}}-4x+\displaystyle \frac{7}{2} & =0\\\therefore {{x}^{2}}-8x+7 & =0\\\therefore (x-1)(x-7) & =0\\\therefore x=1\text{ } & \text{or }x=7\end{align*}[/latex]
y-intercept: Let [latex]\scriptsize x=0[/latex]
[latex]\scriptsize \begin{align*}f(0) & =\displaystyle \frac{1}{2}{{(0)}^{2}}-4(0)+\displaystyle \frac{7}{2}\\ & =\displaystyle \frac{7}{2}\end{align*}[/latex]
The x-coordinate of the TP is [latex]\scriptsize -\displaystyle \frac{b}{{2a}}=-\displaystyle \frac{{(-4)}}{{2\left( {\displaystyle \frac{1}{2}} \right)}}=4[/latex]. Therefore, the A/S is the line [latex]\scriptsize x=4[/latex].
The y-coordinate of the TP can be found by finding [latex]\scriptsize f(4)[/latex]
[latex]\scriptsize \displaystyle \begin{align*}f(4)&=\displaystyle \frac{1}{2}{{(4)}^{2}}-4(4)+\displaystyle \frac{7}{2}\\&=8-16+\displaystyle \frac{7}{2}\\&=-4.5\end{align*}[/latex]
[latex]\scriptsize a \gt 0[/latex], so the TP is a minimum.
Exercise 1.3
Question adapted from NC(V) Mathematics First Paper November 2014
Given [latex]\scriptsize y=-{{x}^{2}}+2x+3[/latex]:
- Make a neat sketch of the graph showing all intercepts with the axes, the TP and the A/S.
- Write down the range of [latex]\scriptsize y=-{{x}^{2}}+2x+3[/latex].
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- That the TP of a quadratic function in the turning point form [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] is [latex]\scriptsize (-p,q)[/latex].
- How to sketch the graph of a quadratic function that is in the turning point form.
- How to turn a quadratic function from standard form into turning point form by completing the square.
- That the TP of a quadratic function in standard form [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex] is [latex]\scriptsize \left( {-\displaystyle \frac{b}{{2a}},-\displaystyle \frac{{{{b}^{2}}-4ac}}{{4a}}} \right)[/latex].
- That the y-intercept of a quadratic function in standard form [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex] is [latex]\scriptsize (0,c)[/latex].
- How to sketch the graph of a quadratic function that is in standard form.
Unit 1: Assessment
Suggested time to complete: 30 minutes
- Given [latex]\scriptsize f(x)=-{{x}^{2}}-2x+3[/latex]:
- Make a neat sketch of the graph showing all intercepts with the axes, the TP and the A/S.
- Write down the axis of symmetry of the graph.
- Write down the domain of the function.
- Write down the range of the function.
(Question adapted from NC(V) Mathematics First Paper Supplementary 2014)
- Make a neat sketch of [latex]\scriptsize y={{(x-2)}^{2}}-7[/latex] showing all intercepts with the axes, the TP and the A/S.
- [latex]\scriptsize y=4{{\left( {x+\displaystyle \frac{7}{2}} \right)}^{2}}-25[/latex]. Make a neat sketch of the function showing all intercepts with the axes, the TP and the A/S.
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
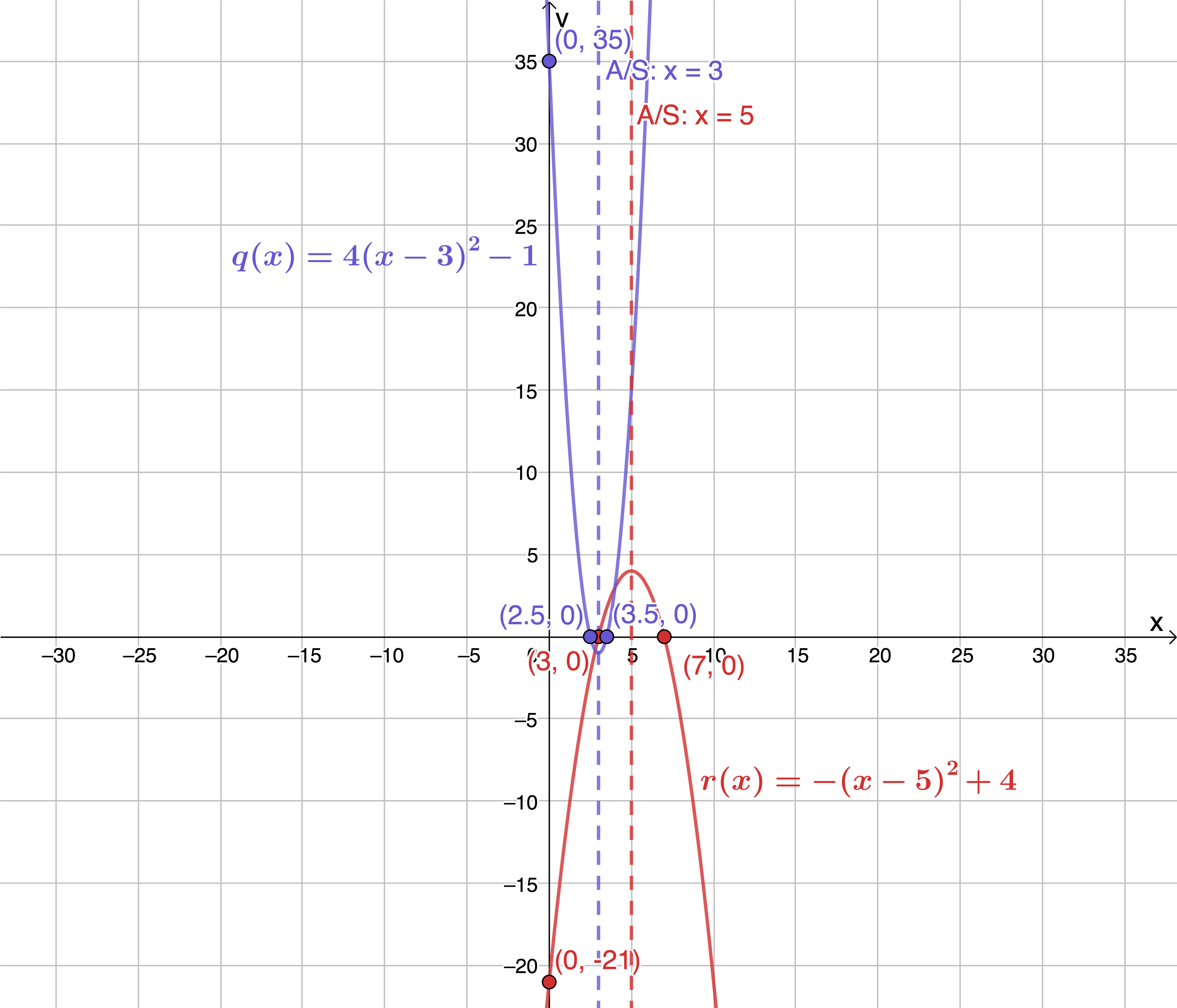
- [latex]\scriptsize q(x)=4{{(x-3)}^{2}}-1[/latex]
- x-intercepts: Let [latex]\scriptsize y=0[/latex]
[latex]\scriptsize \begin{align*}4{{(x-3)}^{2}}-1 & =0\\\therefore 4({{x}^{2}}-6x+9)-1 & =0\\\therefore 4{{x}^{2}}-24x+36-1 & =0\\\therefore 4{{x}^{2}}-24x+35 & =0\\\therefore (2x-5)(2x-7) & =0\\\therefore x=\displaystyle \frac{5}{2}\text{ } & \text{or }x=\displaystyle \frac{7}{2}\end{align*}[/latex] - y-intercept: Let [latex]\scriptsize x=0[/latex]
[latex]\scriptsize \begin{align*}y & =4{{(0-3)}^{2}}-1\\\therefore y & =4\times 9-1\\\therefore y & =35\end{align*}[/latex] - The function is in the turning point form [latex]\scriptsize \displaystyle y=a{{(x+p)}^{2}}+q[/latex]. Therefore, the TP is the point [latex]\scriptsize (-p,q)=(3,-1)[/latex].
- The A/S is the line [latex]\scriptsize x=-p[/latex]. Therefore, the A/S is [latex]\scriptsize x=3[/latex].
- There are no values of [latex]\scriptsize x[/latex] for which [latex]\scriptsize q(x)[/latex] is undefined. Therefore, the domain is [latex]\scriptsize \{x:x\in \mathbb{R}\}[/latex].
- [latex]\scriptsize a \gt 0[/latex]. Therefore, the TP is a minimum and the range is [latex]\scriptsize [-1,\infty )[/latex].
- x-intercepts: Let [latex]\scriptsize y=0[/latex]
- [latex]\scriptsize r(x)=-{{(x-5)}^{2}}+4[/latex].
- x-intercepts: Let [latex]\scriptsize y=0[/latex]
[latex]\scriptsize \begin{align*}-{{(x-5)}^{2}}+4 & =0\\\therefore -({{x}^{2}}-10x+25)+4 & =0\\\therefore -{{x}^{2}}+10x-25+4 & =0\\\therefore -{{x}^{2}}+10x-21 & =0\\\therefore {{x}^{2}}-10x+21 & =0\\\therefore (x-3)(x-7) & =0\\\therefore x=3\text{ } & \text{or }x=7\end{align*}[/latex] - y-intercept: Let [latex]\scriptsize x=0[/latex]
[latex]\scriptsize \begin{align*}y & =-{{(0-5)}^{2}}+4 & \\\therefore y & =-(25)+4\\\therefore y & =-21\end{align*}[/latex] - The function is in the turning point form [latex]\scriptsize \displaystyle y=a{{(x+p)}^{2}}+q[/latex]. Therefore, the TP is the point [latex]\scriptsize (-p,q)=(5,4)[/latex].
- The A/S is the line [latex]\scriptsize x=-p[/latex]. Therefore, the A/S is [latex]\scriptsize x=5[/latex].
- There are no values of [latex]\scriptsize x[/latex] for which [latex]\scriptsize r(x)[/latex] is undefined. Therefore, the domain is [latex]\scriptsize \{x:x\in \mathbb{R}\}[/latex].
- [latex]\scriptsize a \lt 0[/latex]. Therefore, the TP is a maximum and the range is [latex]\scriptsize (\infty ,4][/latex].
- x-intercepts: Let [latex]\scriptsize y=0[/latex]
Exercise 1.2
[latex]\scriptsize \displaystyle \begin{align*}y&=-2{{x}^{2}}+3x-4\\&=-2\left( {{{x}^{2}}-\displaystyle \frac{3}{2}x+2} \right)&& \text{Take out the common factor so the leading coefficient is 1}\\&=-2\left( {{{x}^{2}}-\displaystyle \frac{3}{2}x+\displaystyle \frac{9}{{16}}-\displaystyle \frac{9}{{16}}+2} \right)&& \text{Halve and then square the coefficient of }x\text{ and add and subtract it}\text{.}\\&=-2{{\left( {x-\displaystyle \frac{3}{4}} \right)}^{2}}+\displaystyle \frac{9}{8}-4&& \text{Factorise }{{x}^{2}}-\displaystyle \frac{3}{2}x+\displaystyle \frac{9}{{16}}\text{ into }{{\left( {x-\displaystyle \frac{3}{4}} \right)}^{2}}\\&=-2{{\left( {x-\displaystyle \frac{3}{4}} \right)}^{2}}-\displaystyle \frac{{23}}{8}&& \text{Simplify}\end{align*}[/latex]
Exercise 1.3
- [latex]\scriptsize y=-{{x}^{2}}+2x+3[/latex]
x-intercepts: Let [latex]\scriptsize y=0[/latex]
[latex]\scriptsize \begin{align*}-{{x}^{2}}+2x+3 & =0\\\therefore {{x}^{2}}-2x-3 & =0\\\therefore (x-3)(x+1) & =0\\\therefore x=3\text{ } & \text{or }x=-1\end{align*}[/latex]
.
y-intercept: Let [latex]\scriptsize x=0[/latex]
[latex]\scriptsize \begin{align*}y & =-{{(0)}^{2}}+2(0)+3\\ & =3\end{align*}[/latex]
.
TP:
x-coordinate of the TP: [latex]\scriptsize -\displaystyle \frac{b}{{2a}}=-\displaystyle \frac{2}{{2(-1)}}=1[/latex]
y-coordinate of the TP:
[latex]\scriptsize \begin{align*}y & =-{{(1)}^{2}}+2(1)+3\\ & =-1+2+3\\ & =4\end{align*}[/latex] or [latex]\scriptsize \begin{align*}-\displaystyle \frac{{{{b}^{2}}-4ac}}{{4a}} & =-\displaystyle \frac{{{{2}^{2}}-4(-1)(3)}}{{4(-1)}}\\ & =-\displaystyle \frac{{4+12}}{{(-4)}}=4\end{align*}[/latex]
.
A/S:
[latex]\scriptsize x=-\displaystyle \frac{b}{{2a}}=1[/latex]
.
[latex]\scriptsize a \lt 0[/latex]. Therefore, the TP is a maximum.
.
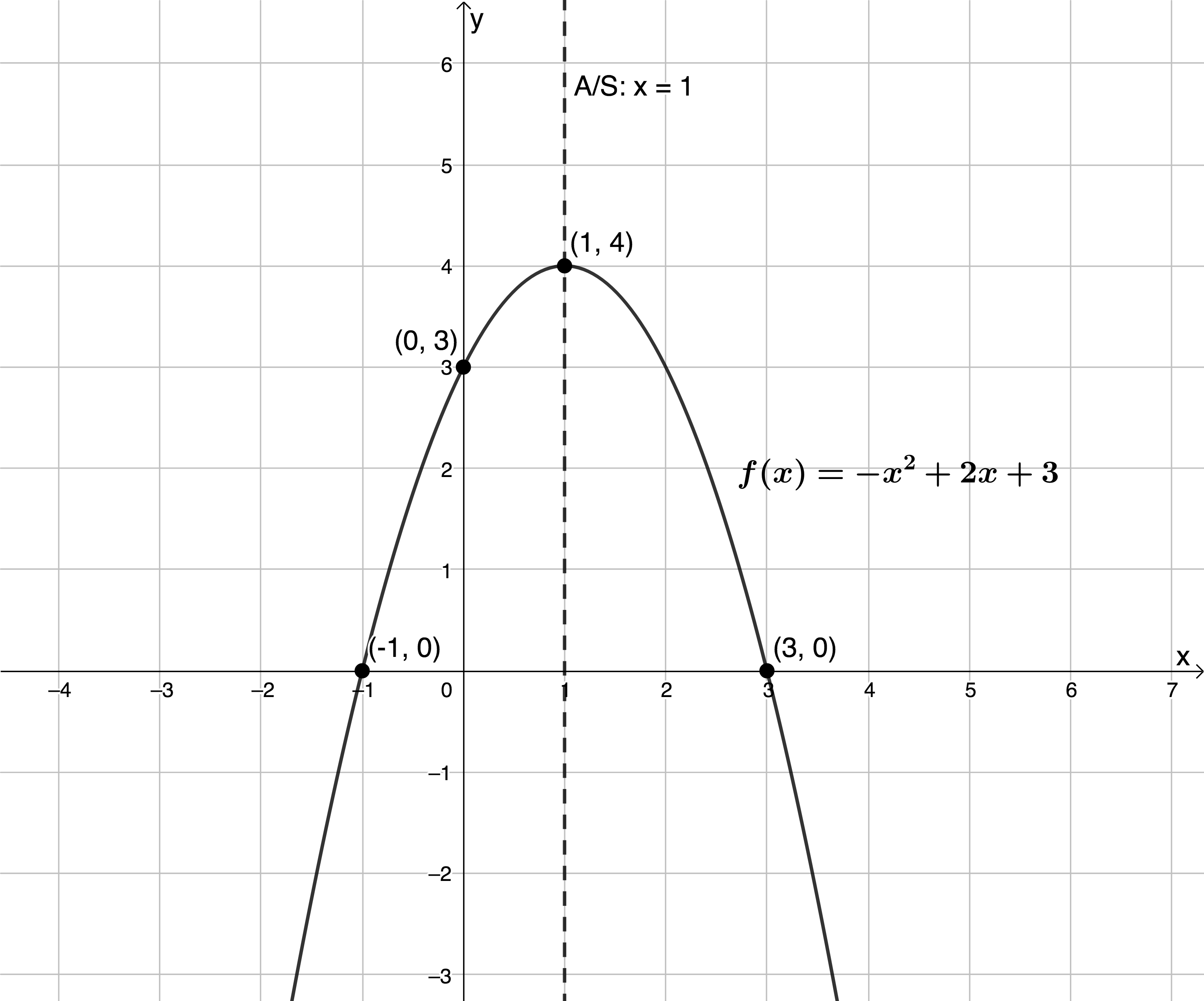
- The range of [latex]\scriptsize f(x)[/latex] is [latex]\scriptsize (-\infty ,4)[/latex].
Unit 1: Assessment
- [latex]\scriptsize f(x)=-{{x}^{2}}-2x+3[/latex]
- x-intercepts: Let [latex]\scriptsize f(x)=0[/latex]
[latex]\scriptsize \begin{align*}-{{x}^{2}}-2x+3 & =0\\\therefore {{x}^{2}}+2x-3 & =0\\\therefore (x+3)(x-1) & =0\\\therefore x=-3\text{ } & \text{or }x=1\end{align*}[/latex]
.
y-intercept: [latex]\scriptsize x=0[/latex]
[latex]\scriptsize \begin{align*}f(0) & =-{{(0)}^{2}}-2(0)+3\\ & =3\end{align*}[/latex]
TP:
x-coordinate of the TP: [latex]\scriptsize -\displaystyle \frac{b}{{2a}}=-\displaystyle \frac{{(-2)}}{{2(-1)}}=-1[/latex]
.
y-coordinate of the TP:
[latex]\scriptsize \begin{align*}y & =-{{(-1)}^{2}}-2(-1)+3\\ & =-1+2+3\\ & =4\end{align*}[/latex] or [latex]\scriptsize \begin{align*}-\displaystyle \frac{{{{b}^{2}}-4ac}}{{4a}} & =-\displaystyle \frac{{{{{(-2)}}^{2}}-4(-1)(3)}}{{4(-1)}}\\ & =-\displaystyle \frac{{4+12}}{{(-4)}}=4\end{align*}[/latex]
.
A/S:
[latex]\scriptsize x=-\displaystyle \frac{b}{{2a}}=-1[/latex]
.
[latex]\scriptsize a \lt 0[/latex]. Therefore, the TP is a maximum.
.
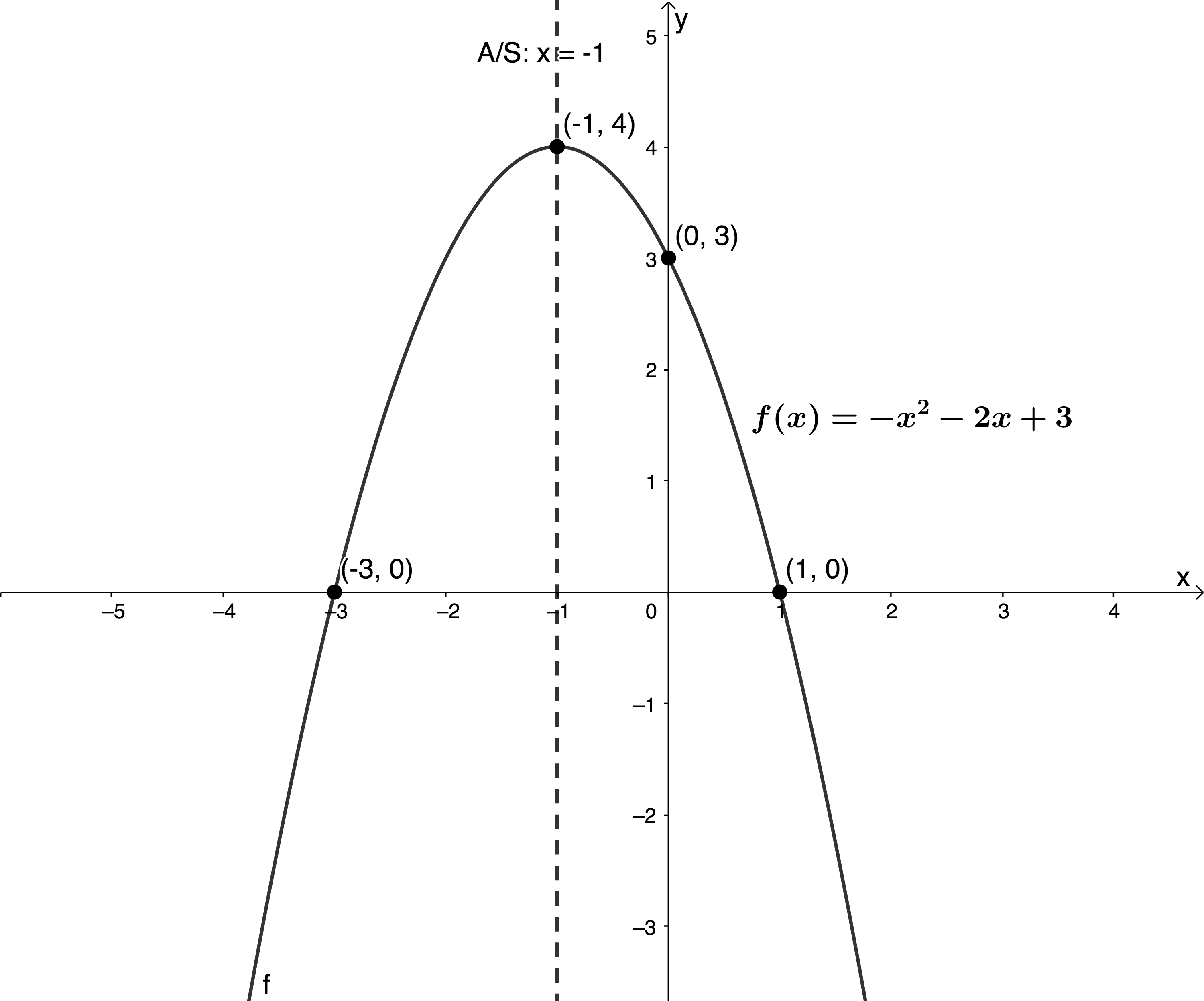
- A/S is the line [latex]\scriptsize x=-1[/latex].
- Domain of [latex]\scriptsize f(x)[/latex] is [latex]\scriptsize \{x:x\in \mathbb{R}\}[/latex]
- Range of [latex]\scriptsize f(x)[/latex] is [latex]\scriptsize \{f(x):f(x)\le 4\}[/latex] or [latex]\scriptsize (-\infty ,4][/latex]
- x-intercepts: Let [latex]\scriptsize f(x)=0[/latex]
- [latex]\scriptsize y={{(x-2)}^{2}}-7[/latex]
x-intercepts: Let [latex]\scriptsize y=0[/latex]
[latex]\scriptsize \displaystyle \begin{align*}{{(x-2)}^{2}}-7 & =0\\\therefore {{x}^{2}}-4x+4-7 & =0\\\therefore {{x}^{2}}-4x-3 & =0\end{align*}[/latex]
Because we cannot factorise this quadratic, we need to solve it using the quadratic formula. If you need help solving quadratic equations with the quadratic formula, see unit 3 of subject outcome 2.3 in level 3.
.
The quadratic formula is [latex]\scriptsize x=\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}[/latex].
In [latex]\scriptsize {{x}^{2}}-4x-3 =0[/latex] [latex]\scriptsize a=1[/latex], [latex]\scriptsize b=-4[/latex] and [latex]\scriptsize c=-3[/latex].
[latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-(-4)\pm \sqrt{{{{{(-4)}}^{2}}-4(1)(-3)}}}}{{2(1)}}\\ & =\displaystyle \frac{{4\pm \sqrt{{16+12}}}}{2}\\ & =\displaystyle \frac{{4\pm \sqrt{{28}}}}{2}\\ & =\displaystyle \frac{{4\pm 2\sqrt{7}}}{2}\\ & =2\pm \sqrt{7}\end{align*}[/latex]
.
y-intercept: [latex]\scriptsize x=0[/latex]
[latex]\scriptsize \displaystyle \begin{align*}y & ={{(0-2)}^{2}}-7\\ & =4-7\\ & =-3\end{align*}[/latex]
.
TP:
[latex]\scriptsize (-p,q)=(2,-7)[/latex]
.
A/S:
[latex]\scriptsize x=2[/latex]
.
[latex]\scriptsize a \gt 0[/latex]. Therefore, the TP is a minimum.
.
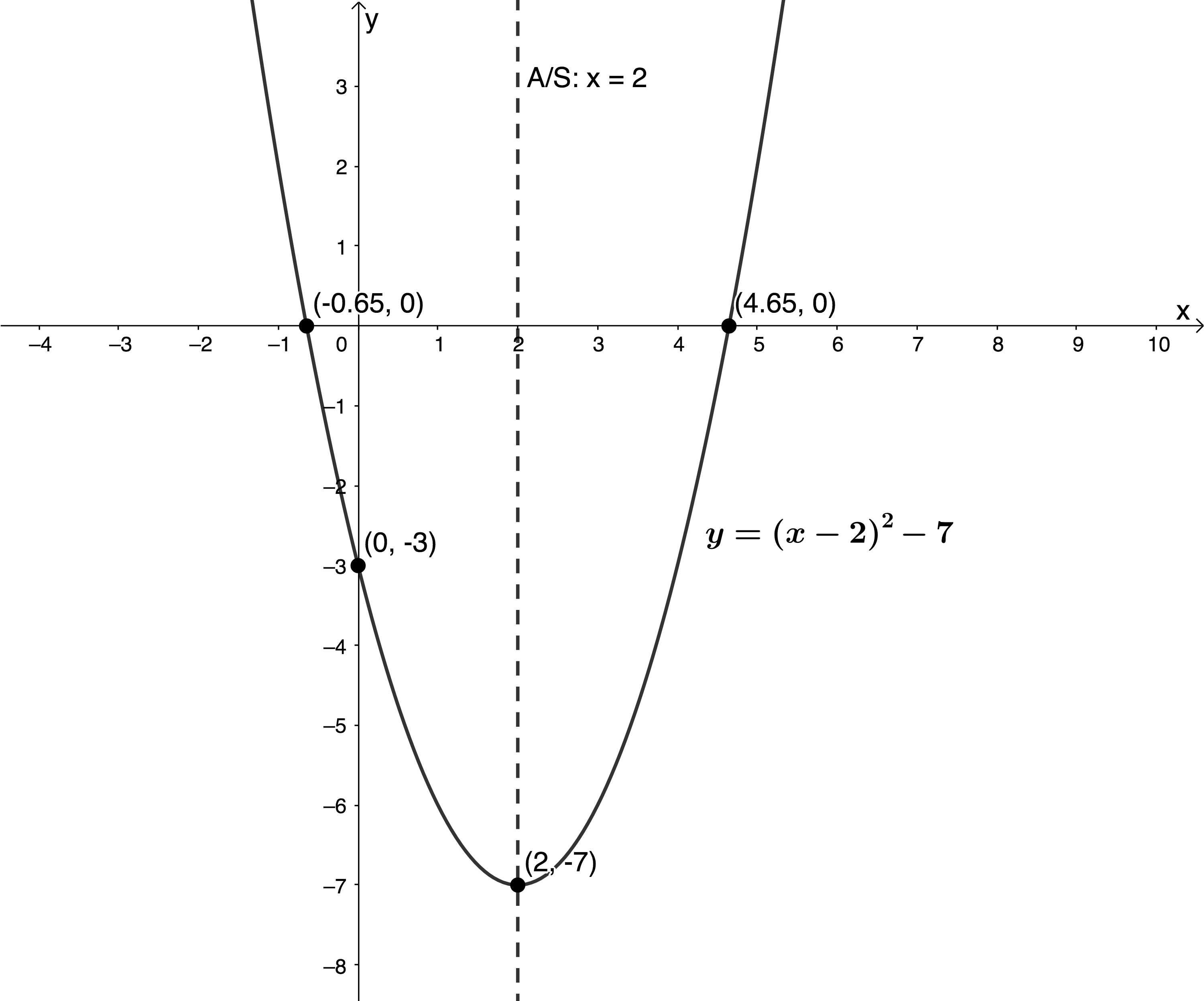
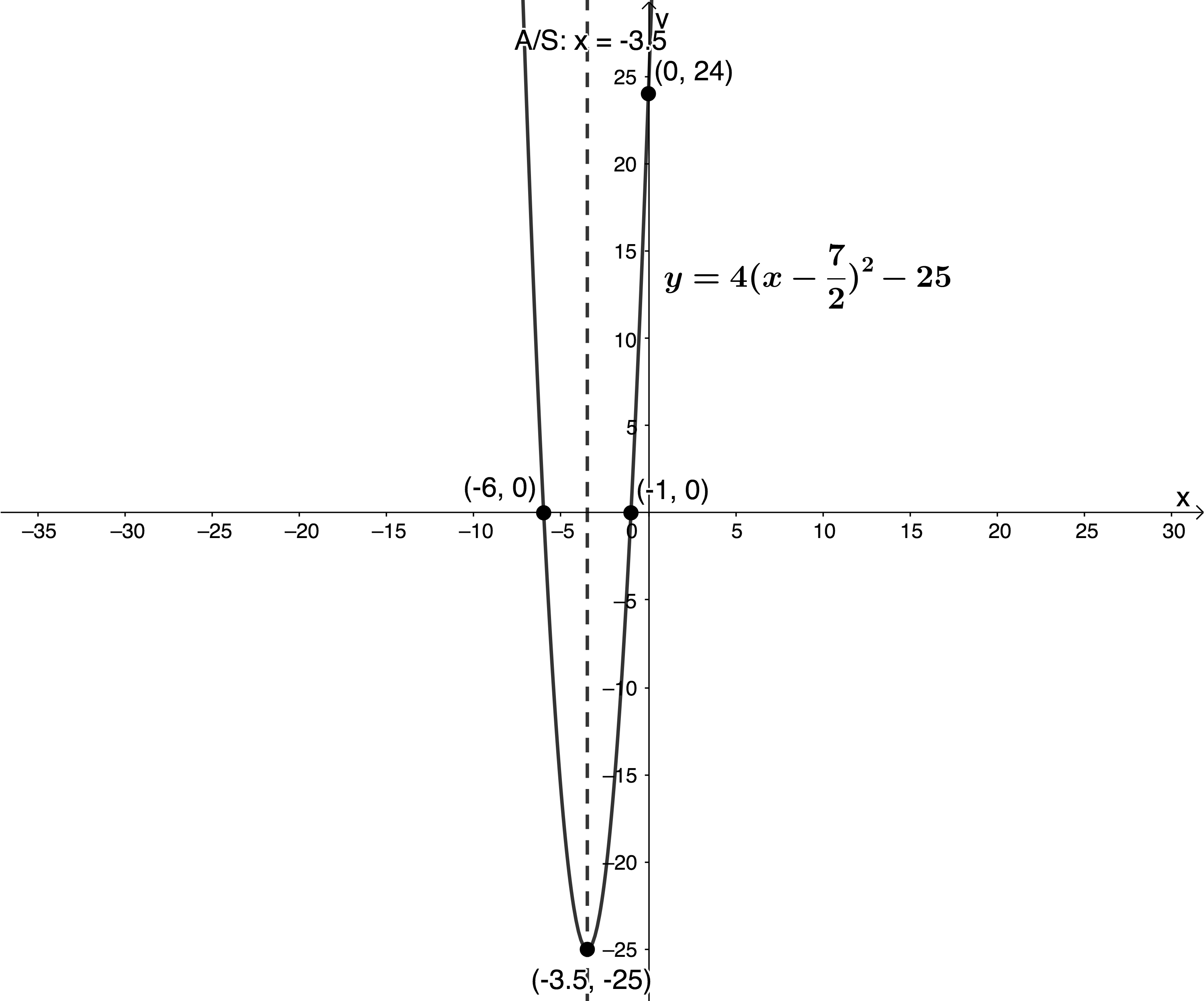
- [latex]\scriptsize y=4{{\left( {x+\displaystyle \frac{7}{2}} \right)}^{2}}-25[/latex].
x-intercepts: Let [latex]\scriptsize y=0[/latex]
[latex]\scriptsize \begin{align*}4{{\left( {x+\displaystyle \frac{7}{2}} \right)}^{2}}-25 & =0\\\therefore 4\left( {{{x}^{2}}+7x+\displaystyle \frac{{49}}{4}} \right)-25 & =0\\\therefore 4{{x}^{2}}+28x+49-25 & =0\\\therefore 4{{x}^{2}}+28x+24 & =0\\\therefore {{x}^{2}}+7x+6 & =0\\\therefore (x+1)(x+6) & =0\\\therefore x=-1\text{ } & \text{or }x=-6\end{align*}[/latex]
.
y-intercept: Let [latex]\scriptsize x=0[/latex]
[latex]\scriptsize \begin{align*}y & =4{{\left( {0+\displaystyle \frac{7}{2}} \right)}^{2}}-25\\ & =4\left( {\displaystyle \frac{{49}}{4}} \right)-25\\&=49-25\\ & =24\end{align*}[/latex]
.
TP:
[latex]\scriptsize (-p,q)=(-\displaystyle \frac{7}{2},-25)[/latex]
.
A/S:
[latex]\scriptsize x=-\displaystyle \frac{7}{2}[/latex]
.
[latex]\scriptsize a \gt 0[/latex]. Therefore, the TP is a minimum.
Media Attributions
- Figure 4 © DHET is licensed under a CC BY-SA (Attribution ShareAlike) license
- activity1.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example 1.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example 1.4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise 1.1A2f © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise 1.3A © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentA1a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentA2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentA3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
