Unit outcomes

By the end of this unit you will be able to:

• Determine limits of functions intuitively.
• Distinguish between the value of a function at a particular point and the limit of the function at that point.

What you should know

Before you start this unit, make sure you can:

• Solve algebraic equations and inequalities. If you need to revise this topic then go over level 3 subject outcome 2.3.
• Sketch and interpret functions. Revise this topic in level 3 subject outcome 2.1.

Introduction

The concept of a limit is essential to all of calculus. Two key ideas led to the development of calculus: 1) the tangent problem, or how to determine the slope of a tangent to a curve at a point and 2) the area problem, or how to determine the area under a curve.

Calculus consists of two related topics: differential calculus and integral calculus. The tangent problem resulted in the formation of differential calculus and the area problem resulted in integral calculus. You will learn about integral calculus and the tangent to a curve in Maths level 4. In level 3 we focus on basic differential calculus and using it to solve optimisation problems.

Limits

Early mathematicians used a limiting process to get better and better approximations of areas of circles. The formal definition of a limit—as we know and apply it today—did not appear until the late 19th century. We begin our quest to understand limits by using an intuitive approach. Once we have a basic understanding of limits, we will look at the formal definition of a limit.

Activity 1.1: Finding limits

Time required: 20 minutes

What you need:

• pen and paper

What to do:

1. Consider the function [latex]\scriptsize y=\displaystyle \frac{{{{x}^{2}}-4}}{{x-2}}[/latex]. Write down the domain of the function.
2. Explain what happens when [latex]\scriptsize x=2[/latex].
3. Copy and complete the table below to see what happens to the function values as [latex]\scriptsize x[/latex] gets closer to [latex]\scriptsize 2[/latex] from the left (values smaller than [latex]\scriptsize 2[/latex]) and the right (values greater than [latex]\scriptsize 2[/latex]).
   

   [latex]\scriptsize x[/latex]	[latex]\scriptsize y=\displaystyle \frac{{{{x}^{2}}-4}}{{x-2}}[/latex]
   [latex]\scriptsize 1.9[/latex]
   [latex]\scriptsize 1.99[/latex]
   [latex]\scriptsize 1.999[/latex]
   [latex]\scriptsize 1.9999[/latex]
   [latex]\scriptsize 2.0001[/latex]
   [latex]\scriptsize 2.001[/latex]
   [latex]\scriptsize 2.01[/latex]
   [latex]\scriptsize 2.1[/latex]

4. What happens to the y-values as [latex]\scriptsize x[/latex] gets closer to [latex]\scriptsize 2[/latex]? Will the function value ever be equal to [latex]\scriptsize 4[/latex]?
5. The graph of the function is shown below.
   .
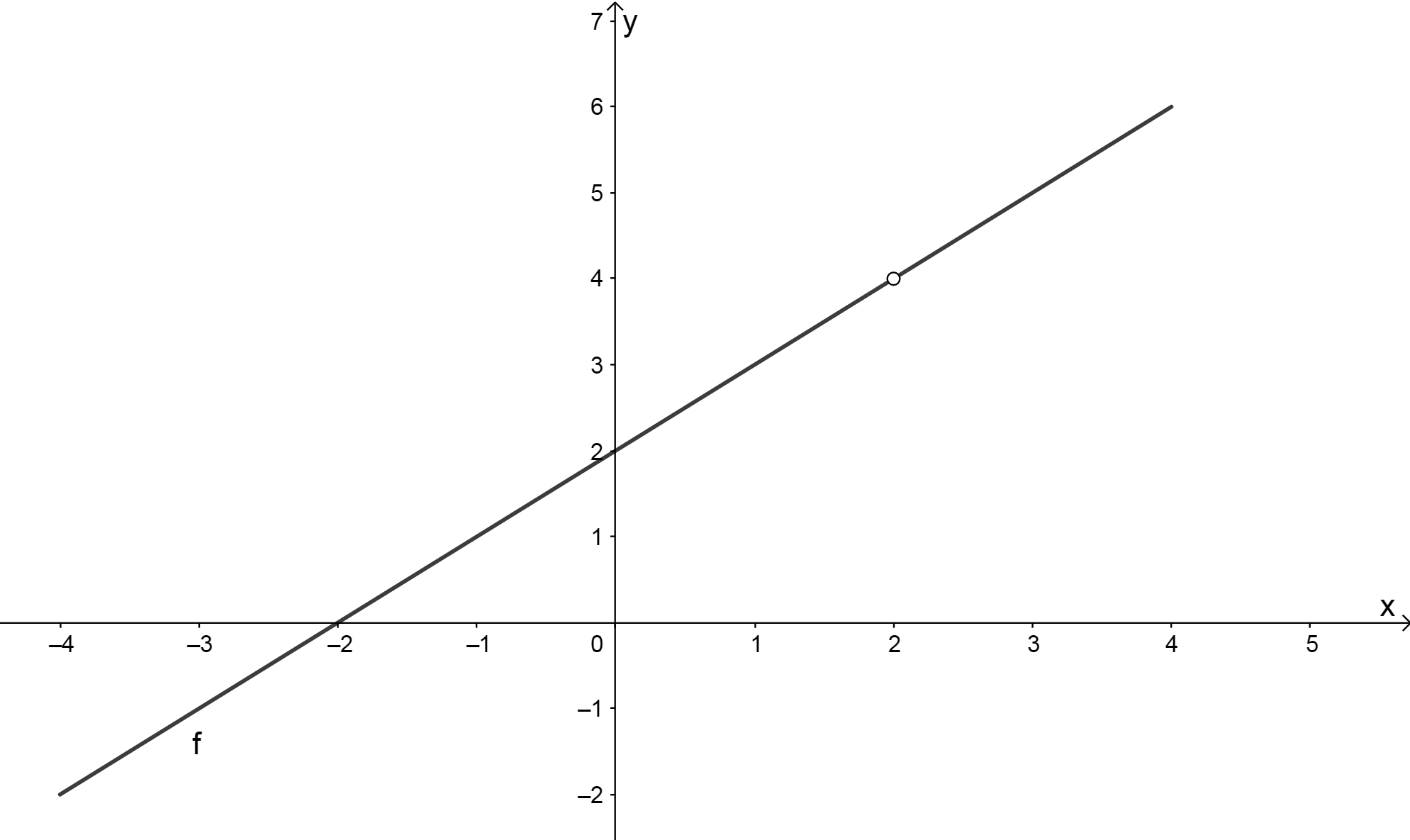   Have a look at the behaviour of the graph at and around [latex]\scriptsize x=2[/latex]. Describe what happens to the graph as [latex]\scriptsize x[/latex] approaches [latex]\scriptsize 2[/latex].

What did you find?

1. We can factorise [latex]\scriptsize y=\displaystyle \frac{{{{x}^{2}}-4}}{{x-2}}[/latex] as [latex]\scriptsize y=\displaystyle \frac{{(x-2)(x+2)}}{{(x-2)}}[/latex] before cancelling the common factor of [latex]\scriptsize x-2[/latex]. We have to note the restriction on the denominator[latex]\scriptsize x\ne 2[/latex]. The domain is [latex]\scriptsize \{x\in \mathbb{R},x\ne 2\}[/latex].
2. If [latex]\scriptsize x=2[/latex], then the denominator becomes [latex]\scriptsize 0[/latex] and the function is not defined. This means that the domain of the function does not include [latex]\scriptsize x=2[/latex].
3. .
   

   [latex]\scriptsize x[/latex]	[latex]\scriptsize y=\displaystyle \frac{{{{x}^{2}}-4}}{{x-2}}[/latex]
   [latex]\scriptsize 1.9[/latex]	[latex]\scriptsize 3.9[/latex]
   [latex]\scriptsize 1.99[/latex]	[latex]\scriptsize 3.99[/latex]
   [latex]\scriptsize 1.999[/latex]	[latex]\scriptsize 3.999[/latex]
   [latex]\scriptsize 1.9999[/latex]	[latex]\scriptsize 3.9999[/latex]
   [latex]\scriptsize 2.0001[/latex]	[latex]\scriptsize 4.0001[/latex]
   [latex]\scriptsize 2.001[/latex]	[latex]\scriptsize 4.001[/latex]
   [latex]\scriptsize 2.01[/latex]	[latex]\scriptsize 4.01[/latex]
   [latex]\scriptsize 2.1[/latex]	[latex]\scriptsize 4.1[/latex]

4. From the table we can see that as [latex]\scriptsize x[/latex] gets closer to [latex]\scriptsize 2[/latex], the y-values get closer and closer to [latex]\scriptsize 4[/latex]. The function will never have a value of [latex]\scriptsize 4[/latex] as we can find no x-value that will make the y-value [latex]\scriptsize 4[/latex].
5. We can see that the graph has a hole at [latex]\scriptsize x=2[/latex], which means that the function is discontinuous. We know that the function is undefined at [latex]\scriptsize x=2[/latex] but if we make this statement and no other, we will give a very incomplete picture of how it behaves as [latex]\scriptsize x[/latex] gets closer to [latex]\scriptsize 2[/latex]. As the values of [latex]\scriptsize x[/latex] approach [latex]\scriptsize 2[/latex] from the left and right, the values of [latex]\scriptsize y[/latex] approach [latex]\scriptsize 4[/latex]. Mathematically, we say that the limit of [latex]\scriptsize f(x)[/latex] as [latex]\scriptsize x[/latex] approaches [latex]\scriptsize 2[/latex] is [latex]\scriptsize 4[/latex].

Notation

When a function approaches the same y-value from the left and from the right, we say that the limit exists. To express the limit of a function we use the following notation: [latex]\scriptsize \underset{{x\to a}}{\mathop{{\lim }}}\,f(x)=L[/latex].

For the function in Activity 1.1, [latex]\scriptsize y=\displaystyle \frac{{{{x}^{2}}-4}}{{x-2}}[/latex], we write [latex]\scriptsize \underset{{x\to 2}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{2}}-4}}{{x-2}}=4[/latex]. This is read as the limit of [latex]\scriptsize \displaystyle \frac{{{{x}^{2}}-4}}{{x-2}}[/latex] as [latex]\scriptsize x[/latex] tends to [latex]\scriptsize 2[/latex] is equal to [latex]\scriptsize 4[/latex]. Again, this does not mean that the function value is [latex]\scriptsize 4[/latex] just that the function approaches [latex]\scriptsize 4[/latex] as [latex]\scriptsize x[/latex] tends to [latex]\scriptsize 2[/latex].

Example 1.1

Determine [latex]\scriptsize \underset{{t\to 6}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{t}^{2}}-36}}{{t-6}}[/latex]

Solution

Simplify the expression:

[latex]\scriptsize \underset{{t\to 6}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{t}^{2}}-36}}{{t-6}}=\underset{{t\to 6}}{\mathop{{\lim }}}\,\displaystyle \frac{{(t-6)(t+6)}}{{t-6}}[/latex] Factorise the numerator.
As [latex]\scriptsize t\to 6[/latex], the denominator [latex]\scriptsize t-6\to 0[/latex], therefore the expression is not defined for [latex]\scriptsize t=6[/latex] since division by zero is undefined.

Cancel all common terms:
[latex]\scriptsize \underset{{t\to 6}}{\mathop{{\lim }}}\,\displaystyle \frac{{(t-6)(t+6)}}{{t-6}}=\underset{{t\to 6}}{\mathop{{\lim }}}\,(t+6)[/latex]

Calculate the limit by substituting the value of [latex]\scriptsize t[/latex]:
[latex]\scriptsize \underset{{t\to 6}}{\mathop{{\lim }}}\,(t+6)=12[/latex]

This means the [latex]\scriptsize \underset{{t\to 6}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{t}^{2}}-36}}{{t-6}}\to 12[/latex] as [latex]\scriptsize t\to 6[/latex], it does not mean that the function value is [latex]\scriptsize 12[/latex] when [latex]\scriptsize t=6[/latex], the function is undefined when [latex]\scriptsize t=6[/latex].

Exercise 1.1

1. If [latex]\scriptsize f(x)=\displaystyle \frac{{{{x}^{2}}+4x-12}}{{x+6}}[/latex]
   1. Determine [latex]\scriptsize \underset{{x\to -6}}{\mathop{{\lim }}}\,f(x)[/latex]
   2. Illustrate the answer graphically.
2. Calculate:
   1. [latex]\scriptsize \underset{{x\to 1}}{\mathop{{\lim }}}\,10[/latex]
   2. [latex]\scriptsize \underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{2}}-9}}{{x-3}}[/latex]

The full solutions are at the end of the unit.

One sided limits

It is possible to have a situation where a function tends to a different limit depending on whether [latex]\scriptsize x[/latex] approaches from the left or the right.
For example, have a look at the following graph:

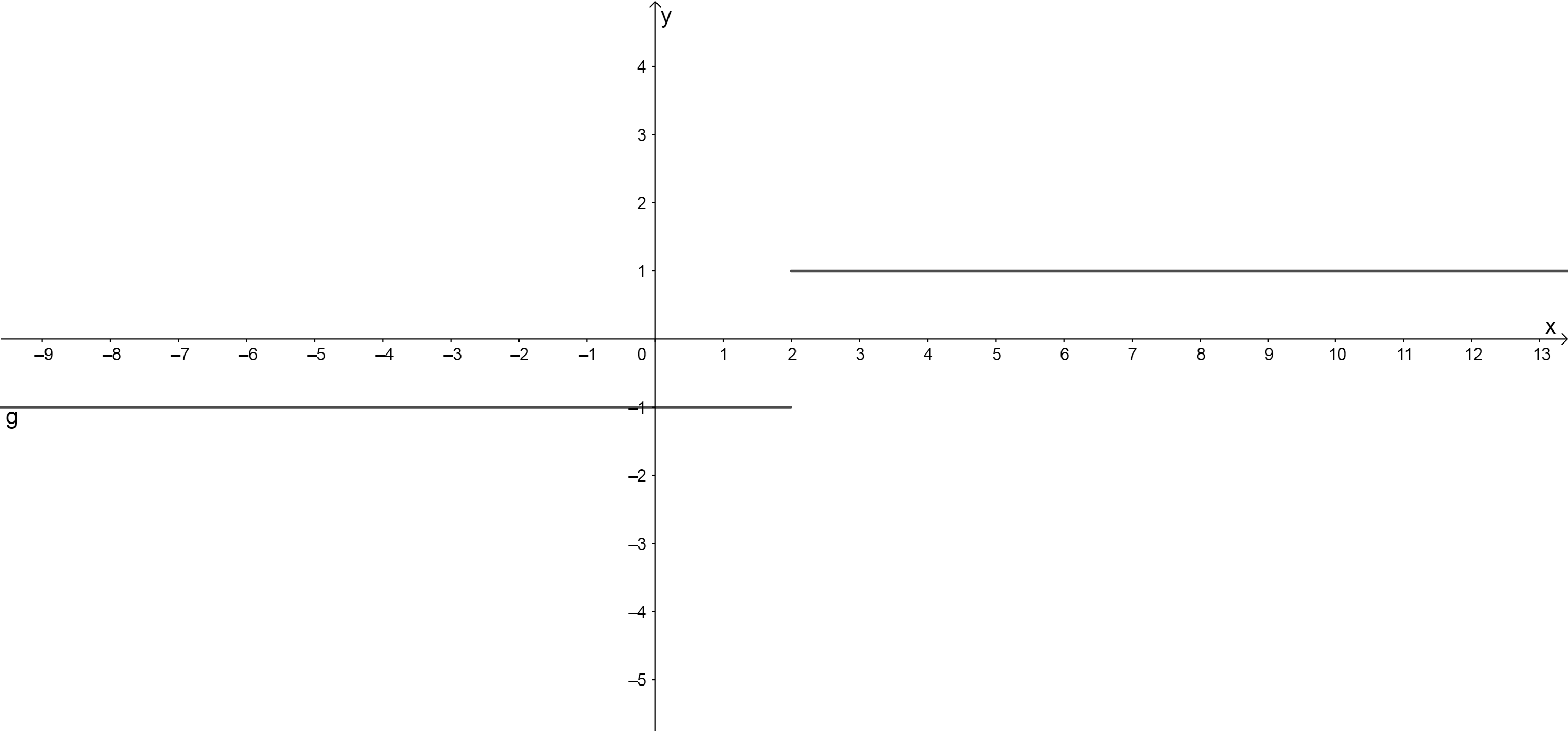
As [latex]\scriptsize x[/latex] approaches [latex]\scriptsize 2[/latex] from the left, [latex]\scriptsize g(x)[/latex] approaches [latex]\scriptsize -1[/latex]. Mathematically, we say that the limit as [latex]\scriptsize x[/latex] tends to [latex]\scriptsize 2[/latex] from the left is −1.

Using notation, we express this idea as [latex]\scriptsize \underset{{x\to {{2}^{-}}}}{\mathop{{\lim }}}\,g(x)=1[/latex]. Where, [latex]\scriptsize x\to {{2}^{-}}[/latex] means [latex]\scriptsize x[/latex] approaches [latex]\scriptsize 2[/latex] from the left.

Similarly, as [latex]\scriptsize x[/latex] approaches [latex]\scriptsize 2[/latex] from the right (or from the positive side), [latex]\scriptsize g(x)[/latex] approaches [latex]\scriptsize 1[/latex]. Using limit notation we write this as [latex]\scriptsize \underset{{x\to {{2}^{+}}}}{\mathop{{\lim }}}\,g(x)=1[/latex]. Where, [latex]\scriptsize x\to {{2}^{+}}[/latex] means [latex]\scriptsize x[/latex] approaches [latex]\scriptsize 2[/latex] from the right.

Therefore, since [latex]\scriptsize g(x)[/latex] does not approach the same value from both sides, we can conclude that the limit as [latex]\scriptsize x[/latex] tends to [latex]\scriptsize 2[/latex] does not exist. We can conclude that it is only when a function approaches the same y-value from the left and from the right that the limit exists.

Limits approaching infinity

Evaluating the limit of a function at a point, or from the left and right of a point, helps us to describe the behaviour of a function around a given value. We can also describe the behaviour of functions as [latex]\scriptsize x\to \infty[/latex].

Limits at infinity are used to describe the behaviour of functions as the independent variable increases or decreases without bound. But, what does infinity really mean?

What is the value of [latex]\scriptsize \displaystyle \frac{1}{\infty }[/latex]? No one really knows as infinity is not an actual number but an idea. Saying [latex]\scriptsize \displaystyle \frac{1}{\infty }[/latex] is similar to saying [latex]\scriptsize \displaystyle \frac{1}{{\text{space}}}[/latex] or [latex]\scriptsize \displaystyle \frac{1}{{\text{hair colour}}}[/latex]. In maths [latex]\scriptsize \displaystyle \frac{1}{\infty }[/latex] is undefined, there is no answer that makes sense.

We cannot reach infinity but we can approach it, using the concept of a limit.

Have a look at the function and table shown in Figure 2.

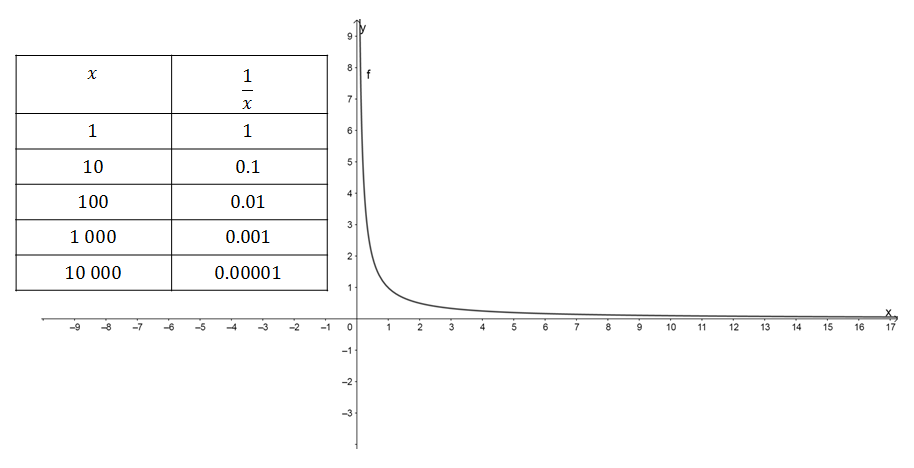
We can see that as the value of [latex]\scriptsize x[/latex] gets bigger, the function [latex]\scriptsize \displaystyle \frac{1}{x}[/latex] gets closer and closer to [latex]\scriptsize 0[/latex]. But, as we discussed previously, we cannot say that [latex]\scriptsize \displaystyle \frac{1}{x}[/latex] is ever equal to zero, no matter how big [latex]\scriptsize x[/latex] gets. So we use the limit to show what is going on as [latex]\scriptsize x[/latex] gets bigger or tends to [latex]\scriptsize \infty[/latex].

To show that [latex]\scriptsize \displaystyle \frac{1}{x}\to 0[/latex] as [latex]\scriptsize x\to \infty[/latex] we write this as [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{1}{x}=0[/latex].

Example 1.2

Find the following:

1. [latex]\scriptsize \underset{{n\to \infty }}{\mathop{{\lim }}}\,2n[/latex]
2. [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,(2{{x}^{2}}-x)[/latex]
3. [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+1}}{{3{{x}^{2}}-1}}[/latex]
4. [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+1}}{{3x-1}}[/latex]
5. [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+x}}{{3x-2}}[/latex]

Solutions

1. As [latex]\scriptsize n\to \infty[/latex], [latex]\scriptsize 2n[/latex] also approaches [latex]\scriptsize \infty[/latex].
   [latex]\scriptsize \therefore \underset{{n\to \infty }}{\mathop{{\lim }}}\,2n=\infty[/latex]
   Remember when you see “[latex]\scriptsize =\infty[/latex]” we cannot actually get to infinity, but using limits we can say the limit is infinity. This is just telling us that the function goes on forever, without limit, as the independent variable gets bigger and bigger in numerical value.
2. As [latex]\scriptsize x\to \infty[/latex], [latex]\scriptsize 2{{x}^{2}}\to +\infty[/latex]
   As [latex]\scriptsize x\to \infty[/latex], [latex]\scriptsize -x\to -\infty[/latex]
   But [latex]\scriptsize {{x}^{2}}[/latex] grows more rapidly than [latex]\scriptsize x[/latex], so [latex]\scriptsize (2{{x}^{2}}-x)[/latex] will head towards [latex]\scriptsize +[/latex]infinity.
   [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\therefore \lim }}}\,(2{{x}^{2}}-x)=\infty[/latex]
3. When we deal with rational functions such as [latex]\scriptsize \displaystyle \frac{{g(x)}}{{h(x)}}[/latex] we must compare the degree (highest powers) of the functions.
   If the degree of [latex]\scriptsize g(x)=h(x)[/latex], then divide the coefficients of the terms with the highest powers. This is the case in this example.
   .
   We see both functions have the same degree of [latex]\scriptsize 2[/latex]; the highest power of[latex]\scriptsize x[/latex]. The coefficient of [latex]\scriptsize {{x}^{2}}[/latex] in the numerator is [latex]\scriptsize 2[/latex]. The coefficient of [latex]\scriptsize {{x}^{2}}[/latex] in the denominator is [latex]\scriptsize 3[/latex].
   .
   [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\therefore \lim }}}\,\displaystyle \frac{{2{{x}^{2}}+1}}{{3{{x}^{2}}-1}}=\displaystyle \frac{2}{3}[/latex]
4. If the degree of [latex]\scriptsize g(x) \lt h(x)[/latex], then the limit is [latex]\scriptsize 0[/latex].
   [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2x+1}}{{3{{x}^{2}}-1}}=0[/latex]
5. If the degree of [latex]\scriptsize g(x) \gt h(x)[/latex], then the limit will either be positive infinity or negative infinity. We have to look at the signs of the terms with the largest exponents in both the numerator and denominator.
   [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+x}}{{3x-2}}=+\infty[/latex]
   This is because both [latex]\scriptsize {{x}^{2}}[/latex] in the numerator and [latex]\scriptsize 3x[/latex] in the denominator are positive.
   While [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{4{{x}^{2}}-5{{x}^{3}}}}{{3x-2}}=-\infty[/latex] because [latex]\scriptsize \displaystyle \frac{{-5}}{3}[/latex] is negative.

Exercise 1.2

Calculate the following:

1. [latex]\scriptsize \displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{2}{{{{x}^{2}}}}[/latex]
2. [latex]\scriptsize \displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,({{x}^{3}}+1)[/latex]
3. [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{6{{x}^{2}}-{{x}^{3}}}}{{2x-1}}[/latex]

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to evaluate limits of a function at a point by factorising.
• How to use the limit from the left and right to determine if the limit of a function exists.
• How to describe a graph by looking at how the function values behave as the independent variable approaches a point that is undefined.
• How to evaluate limits at infinity.

Unit 1: Assessment

Suggested time to complete: 15 minutes

Calculate the following:

1. [latex]\scriptsize \underset{{y\to 1}}{\mathop{{\lim }}}\,\displaystyle \frac{{y-1}}{{y+1}}[/latex]
2. [latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2h+{{h}^{2}}}}{h}[/latex]
3. [latex]\scriptsize \underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{2}}-9}}{{{{x}^{2}}-3x}}[/latex]
4. [latex]\scriptsize \underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{{(4+h)}}^{2}}-16}}{h}[/latex]
5. [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+1}}{{{{x}^{2}}+1}}[/latex]

The full solutions are at the end of the unit.

Unit 1: Solutions

Exercise 1.1

1. If [latex]\scriptsize f(x)=\displaystyle \frac{{{{x}^{2}}+4x-12}}{{x+6}}[/latex]
   1. .
      [latex]\scriptsize \begin{align*}\underset{{x\to -6}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{2}}+4x-12}}{{x+6}} & =\underset{{x\to -6}}{\mathop{{\lim }}}\,\displaystyle \frac{{(x+6)(x-2)}}{{(x+6)}}\text{ Factorise and cancel first}\\ & =\underset{{x\to -6}}{\mathop{{\lim }}}\,(x-2)\text{ Substitute }x\text{ with }-6\\ & =-8\end{align*}[/latex]
   2. .
      
2. .
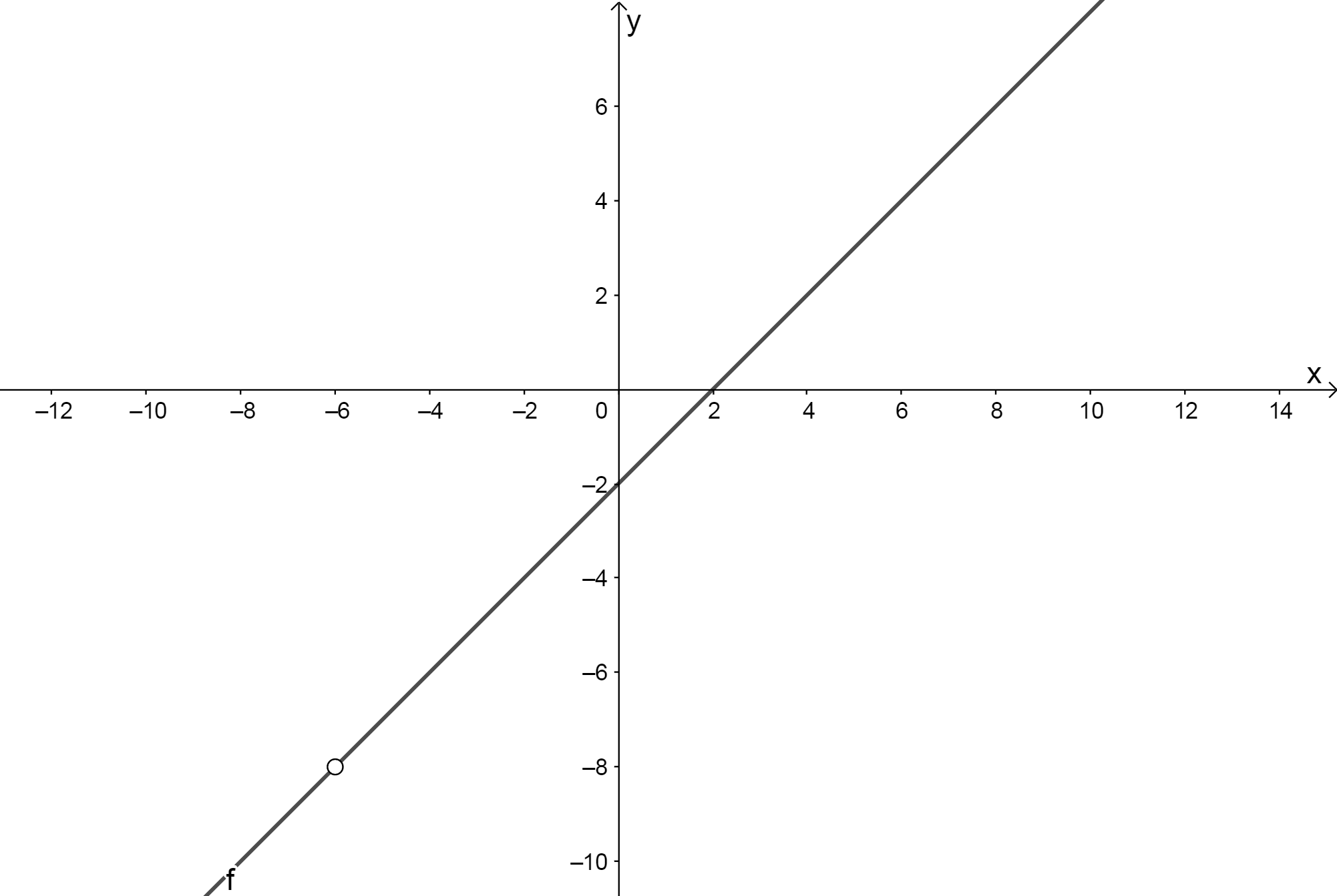
   1. We cannot simplify further and there are no terms to cancel.
      [latex]\scriptsize \underset{{x\to 1}}{\mathop{{\lim }}}\,10=10[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{2}}-9}}{{x-3}}&=\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{(x-3)(x+3)}}{{(x-3)}}\\&=\underset{{x\to 3}}{\mathop{{\lim }}}\,(x+3)\\&=6\end{align*}[/latex]

Back to Exercise 1.1

Exercise 1.2

1. [latex]\scriptsize \displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{2}{{{{x}^{2}}}}=0[/latex]
2. [latex]\scriptsize \displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,({{x}^{3}}+1)=\infty[/latex]
3. [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{6x-{{x}^{3}}}}{{2{{x}^{2}}-1}}=-\infty[/latex]

Back to Exercise 1.2

Unit 1: Assessment

1. .
   [latex]\scriptsize \underset{{y\to 1}}{\mathop{{\lim }}}\,\displaystyle \frac{{y-1}}{{y+1}}=0[/latex]
2. .
   [latex]\scriptsize \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{2h+{{h}^{2}}}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{h(2+h)}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,2+h\\&=2\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{x}^{2}}-9}}{{{{x}^{2}}-3x}}&=\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{(x-3)(x+3)}}{{x(x-3)}}\\&=\underset{{x\to 3}}{\mathop{{\lim }}}\,\displaystyle \frac{{(x+3)}}{x}\\&=\displaystyle \frac{6}{3}\\&=2\end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*}\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{{{{(4+h)}}^{2}}-16}}{h}&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{16+8h+{{h}^{2}}-16}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{8h+{{h}^{2}}}}{h}\\&=\underset{{h\to 0}}{\mathop{{\lim }}}\,\displaystyle \frac{{h(8+h)}}{h}\\&=8\end{align*}[/latex]
5. .
   [latex]\scriptsize \underset{{x\to \infty }}{\mathop{{\lim }}}\,\displaystyle \frac{{2{{x}^{2}}+1}}{{{{x}^{2}}+1}}=2[/latex]

Back to Unit 1: Assessment