Unit outcomes

By the end of this unit you will be able to:

• Apply the appropriate formulae to find the surface area of:
  • right pyramids (with square, equilateral triangle or regular hexagonal bases)
  • right cones
  • spheres.
• Determine and calculate the surface area of combinations of these geometric objects.

What you should know

Before you start this unit, make sure you can:

• find the surface area of right prisms. You can revise surface area of prisms in level 2 subject outcome 3.2 unit 3.

Introduction

The total surface area (TSA) of a 3-D shape is the sum of the areas of all its exposed faces (or outer surfaces). In unit 1 of this subject outcome we calculated the volume of right pyramids, cones and spheres. Now, we will find the surface area of these shapes.

Below is a useful table of formulae we can use to find the surface area of right pyramids, cones and spheres.

Square pyramid		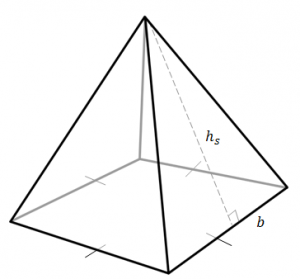[latex]\scriptsize \displaystyle \begin{align*}\text{TSA}&=\text{area of base + area of triangular sides}\\&={{b}^{2}}+\left( {4\displaystyle \frac{1}{2}b{{h}_{s}}\text{ }} \right)\text{ }{{h}_{s}}\text{ is the slant height}\\&=b(b+2{{h}_{s}})\end{align*}[/latex]
Triangular pyramid/ tetrahedron		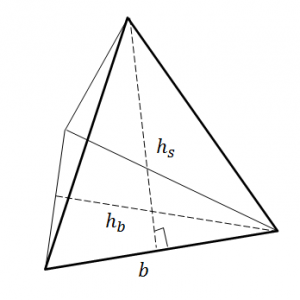[latex]\scriptsize \begin{align*}\text{TSA}&=\text{area of base + area of triangular sides}\\&=\left( {\displaystyle \frac{1}{2}b\times {{h}_{b}}} \right)+3\left( {\displaystyle \frac{1}{2}b\times {{h}_{s}}\text{ }} \right)\end{align*}[/latex]
Hexagonal pyramid		[latex]\scriptsize \displaystyle \begin{align*}\text{TSA}&=\text{area of base + area of triangular sides}\\&=\displaystyle \frac{{3\sqrt{3}}}{2}{{b}^{2}}+6\left( {\displaystyle \frac{1}{2}b\cdot {{h}_{s}}} \right)\\&=\displaystyle \frac{{3\sqrt{3}}}{2}{{b}^{2}}+3b\cdot {{h}_{s}}\\&=3b\left( {\displaystyle \frac{{\sqrt{3}}}{2}b+{{h}_{s}}} \right)\end{align*}[/latex]
Cone		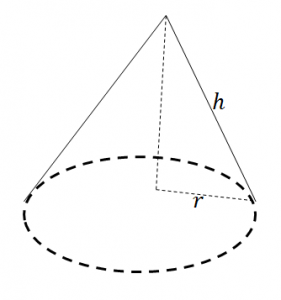[latex]\scriptsize \begin{align*}\text{TSA}&=\text{area of base + area of walls}\\&=\pi {{r}^{2}}+\displaystyle \frac{1}{2}\times 2\pi rh\\&=\pi r(r+h)\end{align*}[/latex]
Sphere		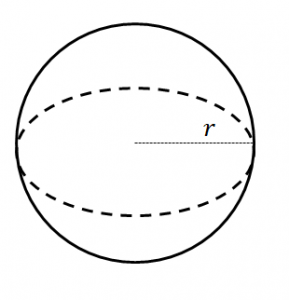[latex]\scriptsize \text{TSA}=4\pi {{r}^{2}}[/latex]

Example 2.1

Find the surface area of the following pyramid (correct to two decimal places):

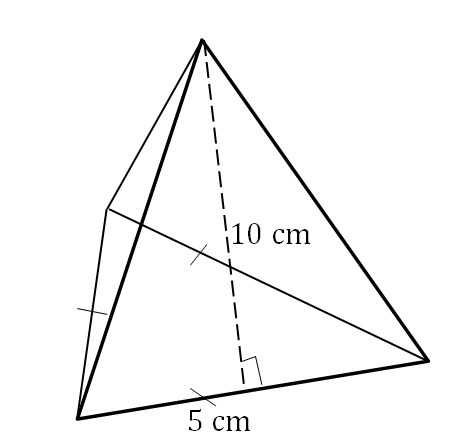
Solution

Here we are given a triangular pyramid with the slant height and length of a base side. If we use the formula:

[latex]\scriptsize \begin{align*}\text{TSA}&=\text{area of base + area of triangular sides}\\&=(\displaystyle \frac{1}{2}b\times {{h}_{b}})+3(\displaystyle \frac{1}{2}b\times {{h}_{s}})\text{ }\end{align*}[/latex]

we see that we need to calculate the length of the height of the base triangle to find the area of the base triangle.

Step 1: Find the area of the base

[latex]\scriptsize \text{Area of base triangle}=(\displaystyle \frac{1}{2}b\times {{h}_{b}})[/latex]

To find the height of the base triangle [latex]\scriptsize {{h}_{b}}[/latex] we use the theorem of Pythagoras.

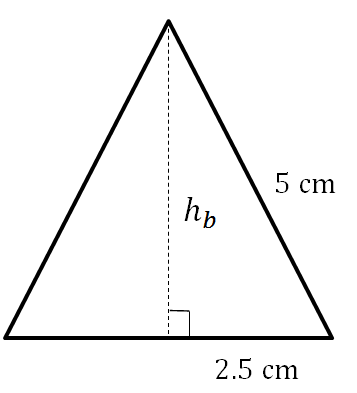
Note that: the altitude of an equilateral triangle bisects its base.

[latex]\scriptsize \begin{align*}{{5}^{2}}&={{h}_{b}}^{2}+{{(2.5)}^{2}}\\{{h}_{b}}&=\sqrt{{{{5}^{2}}-{{{(2.5)}}^{2}}}}\\&=\sqrt{{\displaystyle \frac{{75}}{4}}}\\&=\displaystyle \frac{{5\sqrt{3}}}{2}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\text{Area of base triangle}&=\left( {\displaystyle \frac{1}{2}(5)\times \displaystyle \frac{{5\sqrt{3}}}{2}} \right)\\&=\displaystyle \frac{{25\sqrt{3}}}{4}\text{ c}{{\text{m}}^{2}}\end{align*}[/latex]

Step 2: Find the area of the sides

[latex]\scriptsize \begin{align*}\text{Area of sides}&=3\left( {\displaystyle \frac{1}{2}b\times {{h}_{s}}\text{ }} \right)\\&=3\left( {\displaystyle \frac{1}{2}(5)\times 10\text{ }} \right)\\&=75\text{ c}{{\text{m}}^{2}}\end{align*}[/latex]

Step 3: Find the sum of the areas to find the total surface area

[latex]\scriptsize \displaystyle \frac{{25\sqrt{3}}}{4}\text{ c}{{\text{m}}^{2}}+75\text{ c}{{\text{m}}^{2}}=85.83\text{ c}{{\text{m}}^{2}}[/latex]

The surface area of the triangular pyramid is [latex]\scriptsize 85.83\text{ c}{{\text{m}}^{2}}[/latex].

Example 2.2

Find the surface area of a square based pyramid with base length [latex]\scriptsize 6\text{ cm}[/latex] and slant height of [latex]\scriptsize 11\text{ cm}[/latex].

Solution

We use the formula:

[latex]\scriptsize \displaystyle \begin{align*}\text{TSA}&=\text{area of base + area of triangular sides}\\&={{b}^{2}}+4\left( {\displaystyle \frac{1}{2}b{{h}_{s}}\text{ }} \right)\text{ }{{h}_{s}}\text{ is the slant height}\\&=b(b+2{{h}_{s}})\end{align*}[/latex]

[latex]\scriptsize \displaystyle b=6\text{ cm }{{h}_{s}}=11\text{ cm}[/latex]

[latex]\scriptsize \displaystyle \begin{align*}\text{TSA}&=b(b+2{{h}_{s}})\\&=6(6+2\times 11)\\&=168\text{ c}{{\text{m}}^{2}}\end{align*}[/latex]

The surface area of the square based pyramid is [latex]\scriptsize \displaystyle 168\text{ c}{{\text{m}}^{2}}[/latex].

Example 2.3

Find the surface area of the following cone (correct to 1 decimal place):

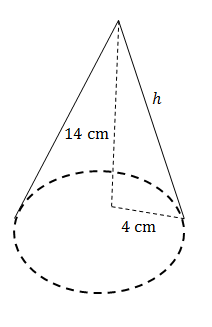
Solution

Write down the formula.

[latex]\scriptsize \begin{align*}\text{TSA}&=\text{area of base + area of walls}\\&=\pi {{r}^{2}}+\displaystyle \frac{1}{2}\times 2\pi rh\\&=\pi r(r+h)\end{align*}[/latex]

To find the slant height we use the theorem of Pythagoras.

[latex]\scriptsize \begin{align*}{{h}^{2}}&={{14}^{2}}+{{4}^{2}}\\&=212\\h&=2\sqrt{{53}}\end{align*}[/latex]

Substitute the values for [latex]\scriptsize \displaystyle r[/latex] and [latex]\scriptsize \displaystyle h[/latex] into the formula.

[latex]\scriptsize \begin{align*}\text{TSA}&=\pi r(r+h)\\&=\pi (4)(4+2\sqrt{{53}})\\&=233.2\text{ c}{{\text{m}}^{2}}\end{align*}[/latex]

The surface area of the cone is [latex]\scriptsize 233.2\text{ c}{{\text{m}}^{2}}[/latex].

Exercise 2.1

1. The Southern African Large Telescope (SALT) is housed in a cylindrical building with a domed roof in the shape of a hemisphere. The height of the building’s wall is [latex]\scriptsize \displaystyle 17\text{ m}[/latex] and the diameter is [latex]\scriptsize \displaystyle 26\text{ m}[/latex].
   
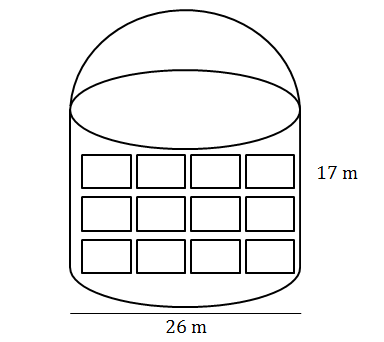
   1. Calculate the total surface area of the building. (HINT: The surface area of a hemisphere is half the surface area of a sphere).
   2. Calculate the total volume of the building.
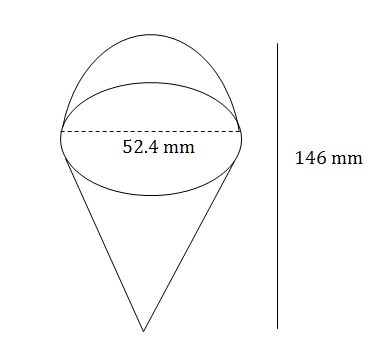
2. An ice-cream cone has a diameter of [latex]\scriptsize \displaystyle 52.4\text{ mm}[/latex] and a total height of [latex]\scriptsize \displaystyle 146\text{ mm}[/latex]. Calculate the surface area of the ice-cream and the cone.
   
3. A pyramid with a square base has base sides each of [latex]\scriptsize \displaystyle 4[/latex] units long. The vertical height of the pyramid is [latex]\scriptsize 8.77[/latex] units, and the slant height of the pyramid is [latex]\scriptsize \displaystyle 9[/latex] units. Determine the surface area of the pyramid.

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to find the surface area of right pyramids.
• How to find the surface area of cones.
• How to find the surface area of spheres.

Unit 2: Assessment

Suggested time to complete: 20 minutes

1. The solid below is made of a cube and a square pyramid:
   
   1. Find the surface area of the solid. Give your answers to two decimal places.
   2. Now determine the volume of the shape. Give your answer to the nearest integer value.
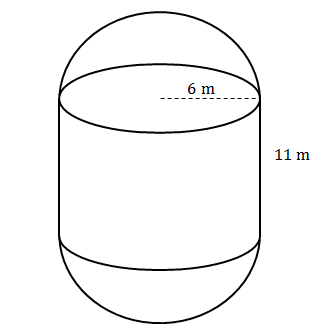
2. Find the surface area of the following capsule:
   
3. Sammy needs to cover a pyramid with a hexagonal base and sides of length of [latex]\scriptsize 550\text{ mm}[/latex]. The slant height of the pyramid is [latex]\scriptsize 200\text{ mm}[/latex]. If the cost of the material needed to cover the pyramid is [latex]\scriptsize \text{R}100[/latex] per square metre. What is the total cost to cover the pyramid?

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. .
   1. [latex]\scriptsize \displaystyle \text{Total surface area }\!\!~\!\!\text{ }=\text{surface area of dome}+\text{surface area of cylinder}[/latex]
      [latex]\scriptsize \begin{align*}\text{TSA}&=\displaystyle \frac{1}{2}(4\pi {{r}^{2}})+2\pi rh\\&=\displaystyle \frac{1}{2}[4\pi {{(13)}^{2}}]+2\pi (13)(17)\\&=780\pi \text{ }{{\text{m}}^{2}}\\&=2\text{ }450\text{ }{{\text{m}}^{2}}\end{align*}[/latex]
   2. [latex]\scriptsize \displaystyle \text{Total volume}=\text{volume of dome}+\text{volume of cylinder}[/latex]
      [latex]\scriptsize \begin{align*}V&=\displaystyle \frac{1}{2}\left( {\displaystyle \frac{4}{3}\pi {{r}^{3}}} \right)+\pi {{r}^{2}}h\\&=\displaystyle \frac{2}{3}\pi {{(13)}^{3}}+\pi {{(13)}^{2}}(17)\\&=13\text{ 627 }{{\text{m}}^{3}}\end{align*}[/latex]
2. .
   The vertical height of the cone is [latex]\scriptsize 146\text{ mm}-52.4\text{ mm}=93.6\text{ mm}[/latex].
   Work out the slant height using the theorem of Pythagoras.
   [latex]\scriptsize \begin{align*}{{h}_{s}}^{2}&={{(26.2)}^{2}}+{{(93.6)}^{2}}\\{{h}_{s}}&=\sqrt{{9447.4}}\\&=97.19...\text{ mm}\end{align*}[/latex]
   For the surface area of the cone we consider only the surface area of the walls that make up the cone. [latex]\scriptsize \displaystyle \text{Total surface area }\!\!~\!\!\text{ }=\text{surface area of hemisphere}+\text{surface area of cone}[/latex]
   [latex]\scriptsize \displaystyle \begin{align*}\text{TSA}&=\displaystyle \frac{1}{2}(4\pi {{r}^{2}})+\pi rh\\&=\displaystyle \frac{1}{2}(4\pi {{(26.2)}^{2}})+\pi (26.2)(97.19...)\\&=12\text{ 313}\text{.35 m}{{\text{m}}^{2}}\end{align*}[/latex]
3. .
   [latex]\scriptsize \displaystyle \begin{align*}\text{TSA}&=\text{area of base + area of triangular sides}\\&={{b}^{2}}+4(\displaystyle \frac{1}{2}b{{h}_{s}})\text{ }{{h}_{s}}\text{ is the slant height}\\&=b(b+2{{h}_{s}})\\&=4(4+2\cdot 9)\\&=88\text{ units squared }\end{align*}[/latex]

Back to Exercise 2.1

Unit 2: Assessment

1. .
   1. Note: we must include only the exposed surfaces in the calculation of surface area.
      First, find [latex]\scriptsize \displaystyle {{h}_{s}}[/latex] by using the theorem of Pythagoras.
      [latex]\scriptsize 22\text{ cm}-7\text{ cm}=15\text{ cm is the vertical height of the pyramid}[/latex]
      [latex]\scriptsize \displaystyle \begin{align*}{{h}_{s}}^{2}&={{15}^{2}}+{{3.5}^{2}}\\{{h}_{s}}&=\sqrt{{\displaystyle \frac{{949}}{4}}}\\&=\displaystyle \frac{{\sqrt{{949}}}}{2}\text{ cm}\end{align*}[/latex]
      Next, find the total surface area.
      [latex]\scriptsize \text{TSA}=\text{Surface area of square base pyramid}+\text{surface area of cube}[/latex]
      [latex]\scriptsize \displaystyle \begin{align*}\text{TSA}&=4(\displaystyle \frac{1}{2}b{{h}_{s}})+[{{b}^{2}}+4bh]\\&=2(7\cdot \displaystyle \frac{{\sqrt{{949}}}}{2})+[({{7}^{2}})+4(7)7]\\&=460.64\text{ c}{{\text{m}}^{2}}\end{align*}[/latex]
   2. [latex]\scriptsize \displaystyle \text{Total volume}=\text{volume of pyramid}+\text{volume of cube}[/latex]
      [latex]\scriptsize \begin{align*}V&=\displaystyle \frac{{{{b}^{2}}h}}{3}+{{b}^{3}}\\&=\displaystyle \frac{{{{{(7)}}^{2}}(15)}}{3}+{{(7)}^{3}}\\&=588\text{ c}{{\text{m}}^{3}}\end{align*}[/latex]
2. [latex]\scriptsize \displaystyle \text{Total surface area }\!\!~\!\!\text{ }=\text{surface area of sphere}+\text{surface area of cylinder}[/latex]
   [latex]\scriptsize \begin{align*}\text{TSA}&=4\pi {{r}^{2}}+2\pi rh\\&=4\pi {{(6)}^{2}}+2\pi (6)(11)\\&=276\pi \\&=867.08\text{ }{{\text{m}}^{2}}\end{align*}[/latex]
3. .
   [latex]\scriptsize \displaystyle \begin{align*}\text{TSA}&=\text{area of base + area of triangular sides}\\&=\displaystyle \frac{{3\sqrt{3}}}{2}{{b}^{2}}+6\left( {\displaystyle \frac{1}{2}b\cdot {{h}_{s}}} \right)\\&=\displaystyle \frac{{3\sqrt{3}}}{2}{{b}^{2}}+3b\cdot {{h}_{s}}\\&=3b\left( {\displaystyle \frac{{\sqrt{3}}}{2}b+{{h}_{s}}} \right)\\&=3(550)(\displaystyle \frac{{\sqrt{3}}}{2}(550)+200)\\&=1\text{ }115\text{ }918.05\text{ m}{{\text{m}}^{2}}\end{align*}[/latex]
   .
   Next, covert from [latex]\scriptsize \text{m}{{\text{m}}^{2}}[/latex] to [latex]\scriptsize {{\text{m}}^{2}}[/latex]
   [latex]\scriptsize \displaystyle \begin{align*}1\text{ }{{\text{m}}^{2}}&=1\text{ }000\text{ }000\text{ m}{{\text{m}}^{2}}\\1\text{ }115\text{ }918.05\text{ m}{{\text{m}}^{2}}&=1.115...\text{ }{{\text{m}}^{2}}\end{align*}[/latex]
   .
   [latex]\scriptsize \begin{align*}\text{Total cost}&=100\times 1.\text{ }115...\\&=\text{R}111.59\end{align*}[/latex]

Back to Unit 2: Assessment