Unit outcomes

By the end of this unit you will be able to:

• Represent complex numbers using an Argand diagram.
• Find the modulus and argument of a complex number. [latex]\scriptsize {{i}^{2}}=-1[/latex]

What you should know

Before you start this unit, make sure you can:

• Define an imaginary number. Refer to unit 1 in this subject outcome if you need help with this.
• Define a complex number. Refer to unit 1 in this subject outcome if you need help with this.
• Write a complex number in standard or rectangular form. Refer to unit 1 in this subject outcome if you need help with this.
• Work with the basic trigonometric ratios sine, cosine and tangent on the Cartesian plane. Refer to unit 1 in level 2 subject outcome 3.6 if you need help with this.

Introduction

In the previous unit, we defined imaginary numbers and complex numbers. We said that a complex number is written in standard (or rectangular form) as [latex]\scriptsize a+bi[/latex]. However, there is another form in which complex numbers can be written, called polar form.

Polar form is very useful in many situations for adding and subtracting complex numbers, especially when these numbers represent vectors.

In this unit, we are going to learn the basics about writing and working with complex numbers in polar form, and how to convert them from standard form to polar form and back again.

The complex number plane

We know that we can plot the position of any real number on a number line. Figure 1 shows a few examples.

But what do we do with complex numbers that have a real and an imaginary part? To plot complex numbers on a number line, we use two numbers lines – one for the real part and one for the imaginary part. We place these two number lines at right angles to each other to represent the complex plane. This is a coordinate system just like the Cartesian plane. The horizontal axis represents the real component, and the vertical axis represents the imaginary component. Complex numbers are then points on the plane, expressed as ordered pairs.

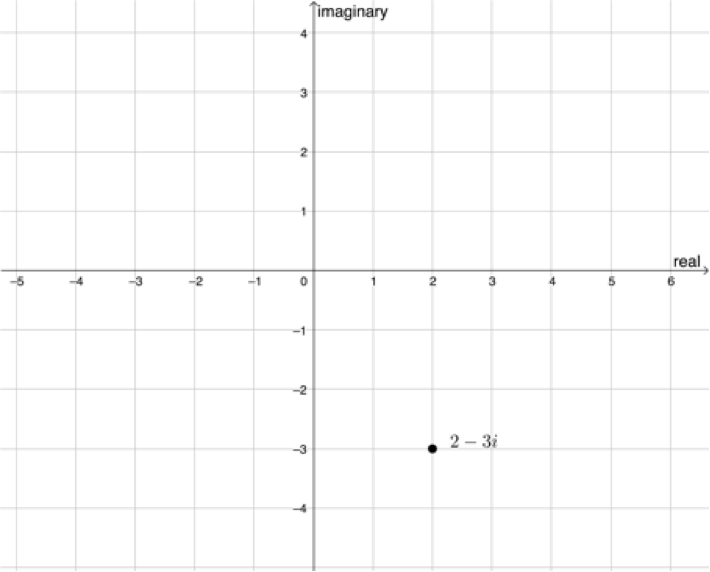
Take the complex number [latex]\scriptsize 2-3i[/latex], for example. We can plot it on the complex plane as shown in Figure 2. It is the point [latex]\scriptsize (2,-3)[/latex].

Take note!

An Argand diagram is a plot of complex numbers as points in the complex plane using the x-axis as the real axis and y-axis as the imaginary axis.

Exercise 2.1

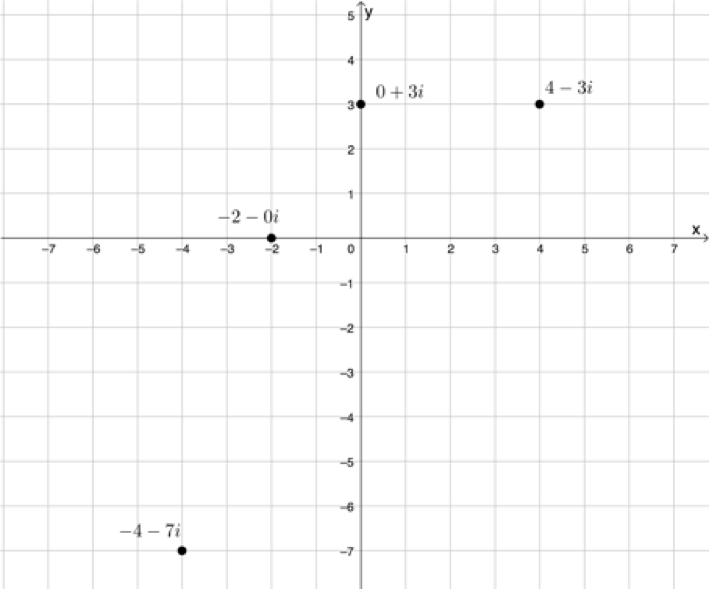
Draw Argand diagrams for the following complex numbers:

1. [latex]\scriptsize 4+3i[/latex]
2. [latex]\scriptsize -4-7i[/latex]
3. [latex]\scriptsize -2[/latex]
4. [latex]\scriptsize 3i[/latex]

The full solutions are at the end of the unit.

The absolute value or modulus of a complex number

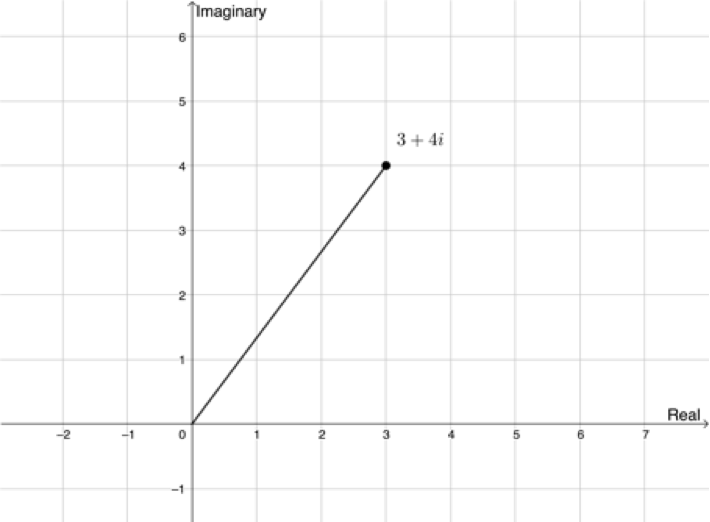
Look at the complex number [latex]\scriptsize 3+4i[/latex] plotted on the complex plane in Figure 3. How far is the point from the origin of the plane? In other words, how long is the line joining the point and the origin in Figure 3? See if you can work this out before reading on.

If we drop a perpendicular line from the point representing [latex]\scriptsize 3+4i[/latex] we will create a right-angled triangle. Now we can use Pythagoras’ theorem to find the length of the line joining [latex]\scriptsize 3+4i[/latex] to the origin as shown in Figure 4.

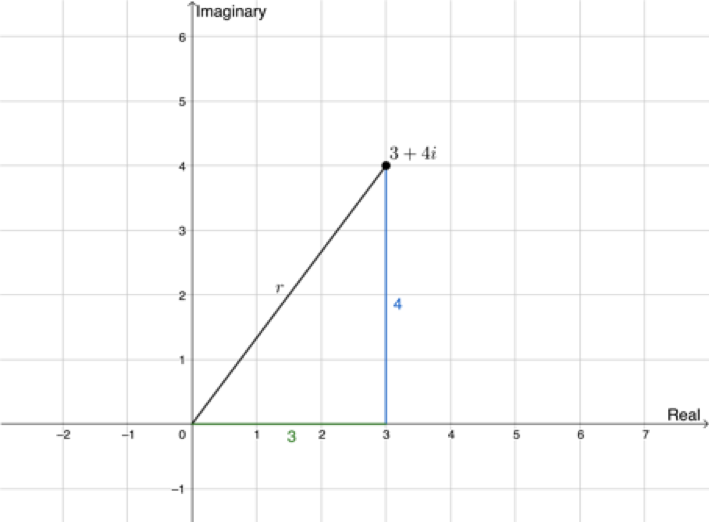
[latex]\scriptsize \begin{align*}{{r}^{2}} & ={{3}^{3}}+{{4}^{2}}\\ & =9+16=25\\\therefore r & =\sqrt{{25}}=5\end{align*}[/latex]

We often represent complex numbers with the letter [latex]\scriptsize z[/latex]. In the example above [latex]\scriptsize z=3+4i[/latex]. We represent the absolute value of [latex]\scriptsize z[/latex] as [latex]\scriptsize \left| z \right|[/latex]. Therefore, if [latex]\scriptsize z=3+4i[/latex], then [latex]\scriptsize \left| z \right|=5[/latex]. For this reason, the complex plane is also known as the z-plane.

Example 2.1

Given [latex]\scriptsize z=3-4i[/latex], find [latex]\scriptsize \left| z \right|[/latex].

Solution

We can plot the complex number [latex]\scriptsize z=3-4i[/latex] on the complex plane.

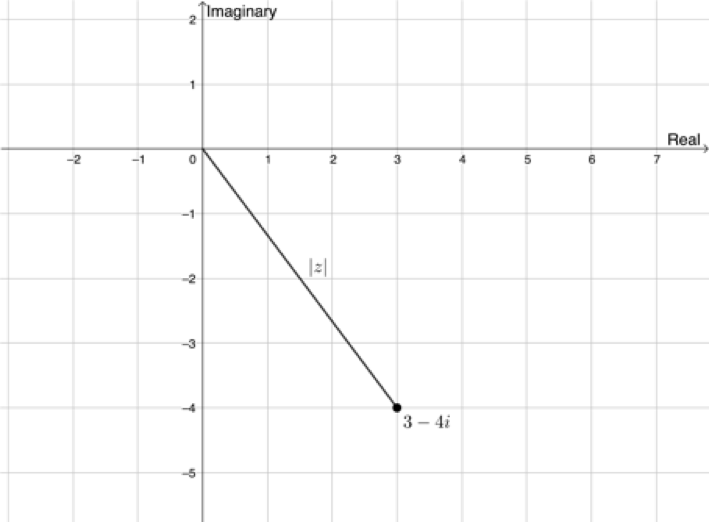
[latex]\scriptsize \begin{align*}\left| z \right|&=\sqrt{{{{x}^{2}}+{{y}^{2}}}}&& x\text{ is the real part and }y\text{ is the imaginary part}\\&=\sqrt{{9+16}}\\&=5\end{align*}[/latex]

Exercise 2.2

Find [latex]\scriptsize \left| z \right|[/latex] in each case:

1. [latex]\scriptsize z=1-7i[/latex]
2. [latex]\scriptsize z=2-6i[/latex]
3. [latex]\scriptsize z=-5+3i[/latex]
4. [latex]\scriptsize z=3-\sqrt{{-6}}[/latex]

The full solutions are at the end of the unit.

Take note!

The absolute value of [latex]\scriptsize z[/latex], [latex]\scriptsize \left| z \right|[/latex], is also called the modulus of [latex]\scriptsize z[/latex].

The argument of complex numbers

You may have noticed in the previous section that the modulus alone is not enough to fully define a complex number on the complex plane. Have a look at Figure 5. Here we have two complex numbers plotted, [latex]\scriptsize {{z}_{1}}=4+3i[/latex] and [latex]\scriptsize {{z}_{2}}=3-4i[/latex]. Work out the value of [latex]\scriptsize \left| z \right|[/latex] (or the modulus) of each number.

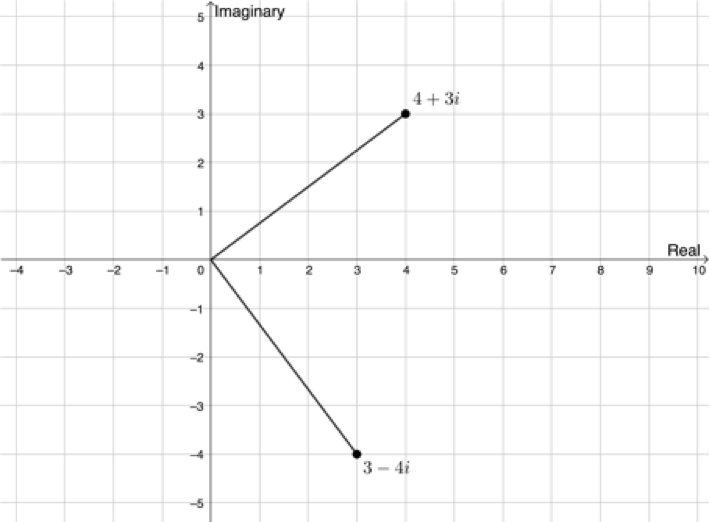
[latex]\scriptsize \begin{align*}\left| {{{z}_{1}}} \right| & =\sqrt{{{{4}^{2}}+{{3}^{2}}}}\\ & =\sqrt{{25}}\\ & =5\end{align*}[/latex] [latex]\scriptsize \begin{align*}\left| {{{z}_{2}}} \right| & =\sqrt{{{{3}^{2}}+{{{(-4)}}^{2}}}}\\ & =\sqrt{{25}}\\ & =5\end{align*}[/latex]

The modulus is the same in both cases, even though the points are different. In order to differentiate these two points, we also need to know the angle that the line representing the modulus makes with the positive x-axis, as shown in Figure 6.

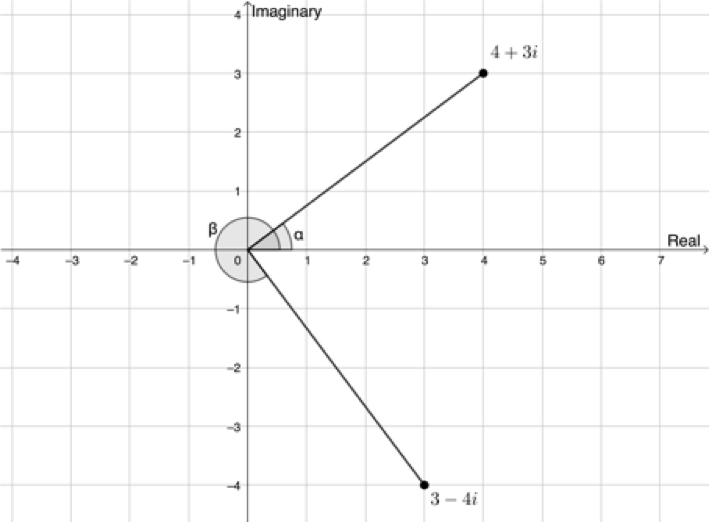
But how can we find the size of these angles? Thankfully, we can use trigonometry to solve this problem.

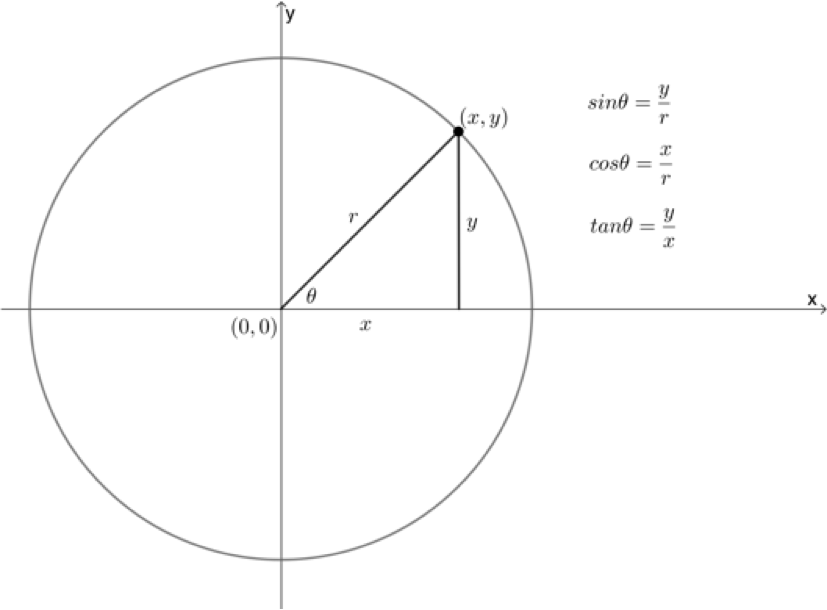
In level 2 subject outcome 3.6 unit 1 we learnt that [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex], [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}[/latex] and [latex]\scriptsize \tan \theta =\displaystyle \frac{y}{x}[/latex] (Figure 7).

From Figure 6 we can say that [latex]\scriptsize \sin \alpha =\displaystyle \frac{y}{r}=\displaystyle \frac{3}{5}[/latex] or that [latex]\scriptsize \cos \alpha =\displaystyle \frac{x}{r}=\displaystyle \frac{4}{5}[/latex]. Therefore, we can calculate the size of [latex]\scriptsize \alpha[/latex]. [latex]\scriptsize \alpha ={{36.870}^\circ}[/latex]. This answer makes sense as we can see that [latex]\scriptsize {{z}_{1}}=4+3i[/latex] is in the first quadrant.

Also, from Figure 6, we can say that [latex]\scriptsize \sin \beta =\displaystyle \frac{y}{r}=\displaystyle \frac{{-4}}{5}[/latex] or that [latex]\scriptsize \cos \beta =\displaystyle \frac{x}{r}=\displaystyle \frac{3}{5}[/latex]. Therefore, we can calculate the size of [latex]\scriptsize \beta[/latex]. [latex]\scriptsize \beta =-{{53.130}^\circ}[/latex]. This makes sense as we can see that [latex]\scriptsize {{z}_{2}}=3-4i[/latex] is in the fourth quadrant.

The angle between the line representing the modulus and the positive x-axis is called the argument. With the modulus and the argument, we can uniquely specify the position of any complex number on the complex plane.

Take note!

The value of the modulus ([latex]\scriptsize \left| z \right|[/latex]) is the same as the value of [latex]\scriptsize r[/latex] in [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex] or [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}[/latex].

Take note!

When calculating the argument, it is important that you draw a sketch of the position of [latex]\scriptsize z[/latex] on the complex plane in order to determine which quadrant the point is in. The three trigonometric ratios still follow the CAST diagram on the complex plane.

Example 2.2

Represent [latex]\scriptsize z=-1+\sqrt{{-3}}[/latex]on an Argand diagram and then determine the modulus and the argument.

Solution

First write the complex number in standard form.
[latex]\scriptsize z=-1+\sqrt{{-3}}=-1+\sqrt{3}i[/latex]

Now, plot the point on the complex plane to determine the quadrant in which it lies.

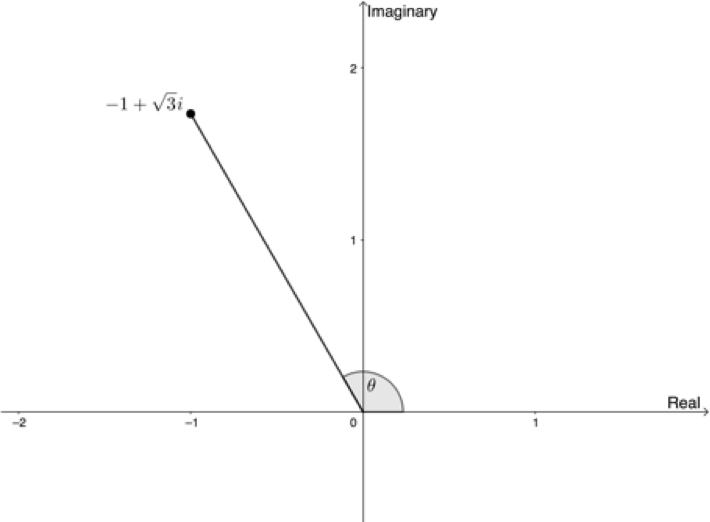
[latex]\scriptsize z[/latex] lies in the second quadrant.

[latex]\scriptsize \begin{align*}\left| z \right| & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{{(-1)}}^{2}}+{{{\left( {\sqrt{3}} \right)}}^{2}}}}\\ & =\sqrt{{1+3}}\\ & =2\end{align*}[/latex]

[latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{y}{r}=\displaystyle \frac{{\sqrt{3}}}{2}\\ & \therefore \theta ={{60}^\circ}\end{align*}[/latex]

But [latex]\scriptsize z[/latex] lies in the second quadrant. Therefore, [latex]\scriptsize \theta ={{180}^\circ}-{{60}^\circ}={{120}^\circ}[/latex].

Take note!

When finding the argument, remember that you need to pay attention to which quadrant the complex number is in. A useful strategy can be to make the ratio for [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex] or [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}[/latex] positive initially, in order to find the reference acute angle [latex]\scriptsize \theta[/latex] and then to transfer this angle into the necessary quadrant as follows:

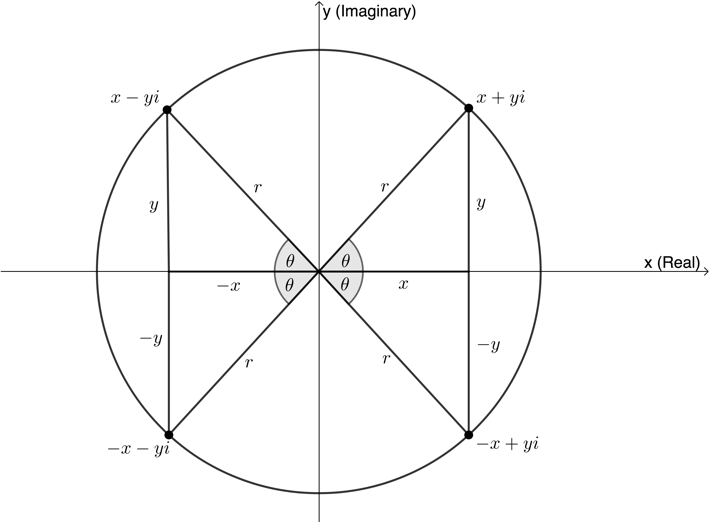
• Second quadrant: [latex]\scriptsize {{180}^\circ}-\theta[/latex]
• Third quadrant: [latex]\scriptsize {{180}^\circ}+\theta[/latex]
• Fourth quadrant: [latex]\scriptsize {{360}^\circ}-\theta[/latex]

Take note!

Remember the three special angles of [latex]\scriptsize {{30}^\circ}[/latex], [latex]\scriptsize {{45}^\circ}[/latex] and [latex]\scriptsize {{60}^\circ}[/latex].

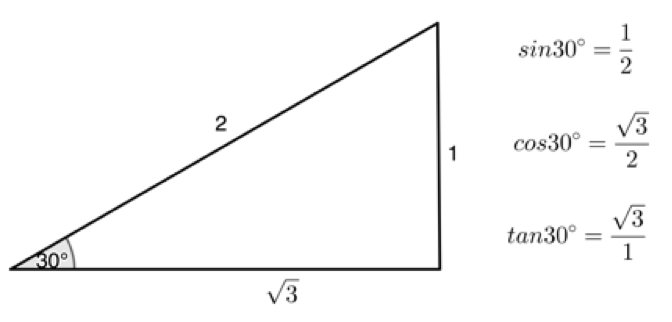
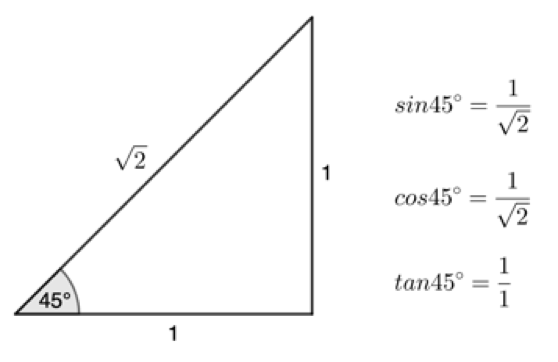
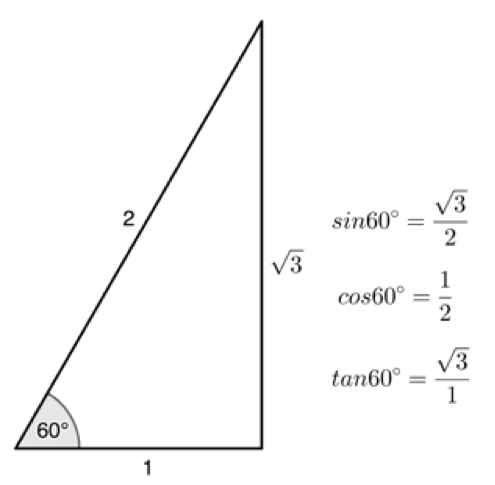
Exercise 2.3

Plot the following on an Argand diagram and then determine the modulus and the argument for each:

1. [latex]\scriptsize z=-1-\sqrt{{-3}}[/latex]
2. [latex]\scriptsize z=2-2i[/latex]
3. [latex]\scriptsize z=-3-4i[/latex]

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to represent complex numbers using an Argand diagram.
• How to find the absolute value or the modulus of a complex number.
• How to find the argument (the angle between the line representing the modulus and the positive x-axis) of a complex number.

Unit 2: Assessment

Suggested time to complete: 15 minutes

Represent the following on an Argand diagram and then determine the modulus and the argument:

1. [latex]\scriptsize z=\sqrt{2}-i[/latex]
2. [latex]\scriptsize z=5+12i[/latex]
3. [latex]\scriptsize z=\sqrt{3}-i[/latex]

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

The answers for questions 1 to 4 are shown below:

Back to Exercise 2.1

Exercise 2.2

1. .
   [latex]\scriptsize \begin{align*} \mid z \mid &=\sqrt{1^2+(-7)^2}\\ &=\sqrt{1+49}\\ &=\sqrt{50}\\ &=\sqrt{(25)(2)}\\ &=5\sqrt{2} \end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*} \mid z \mid &=\sqrt{2^2+(-6)^2}\\ &=\sqrt{4+36}\\ &=\sqrt{40}\\ &=\sqrt{(4)(10)}\\ &=2\sqrt{10} \end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*} \mid z \mid &=\sqrt{(-5)^2+3^2}\\ &=\sqrt{25+9}\\ &=\sqrt{34} \end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*} 3-\sqrt{-6}&=3-\sqrt{6}i\\ \therefore \mid z \mid &=\sqrt{3^2+(-6)^2}\\ &=\sqrt{9+6}\\ &=\sqrt{15} \end{align*}[/latex]

Back to Exercise 2.2

Exercise 2.3

1. [latex]\scriptsize z=-1-\sqrt{{-3}}=-1-\sqrt{3}i[/latex]
   
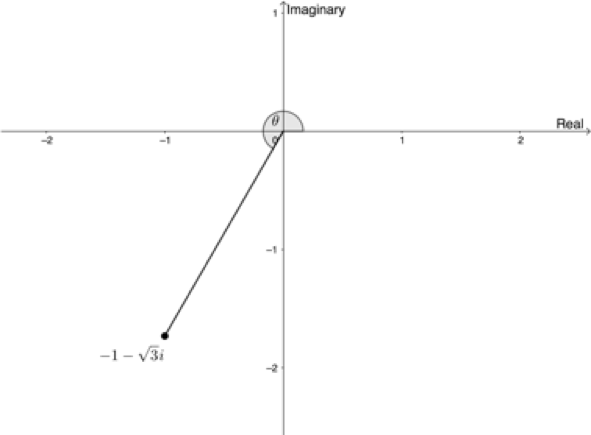
   [latex]\scriptsize \begin{align*}\left| z \right| & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{{(-1)}}^{2}}+{{{(-\sqrt{3})}}^{2}}}}\\ & =\sqrt{{1+3}}\\ & =\sqrt{4}\\ & =2\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{{-\sqrt{3}}}{2}\\\therefore \theta & ={{180}^\circ}+{{60}^\circ}={{240}^\circ}\end{align*}[/latex]
2. [latex]\scriptsize z=2-2i[/latex]
   
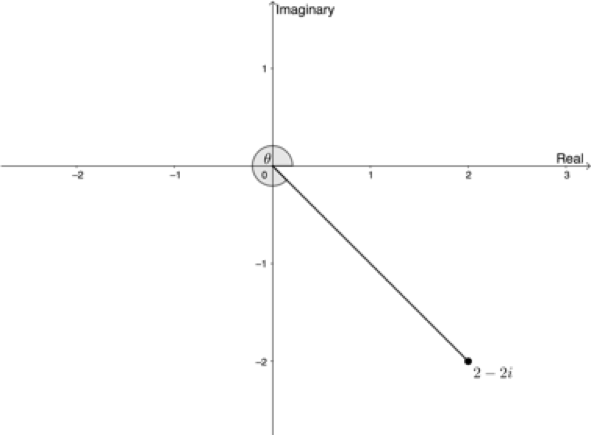
   [latex]\scriptsize \begin{align*}\left| z \right| & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{2}^{2}}+{{{(-2)}}^{2}}}}\\ & =\sqrt{{4+4}}\\ & =\sqrt{8}\\ & =2\sqrt{2}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{{-2}}{{2\sqrt{2}}}=\displaystyle \frac{{-1}}{{\sqrt{2}}}\\\therefore \theta & =-{{45}^\circ}\quad \text{or}\quad \theta ={{360}^\circ}-{{45}^\circ}={{315}^\circ}\end{align*}[/latex]
3. [latex]\scriptsize -3-4i[/latex]
   
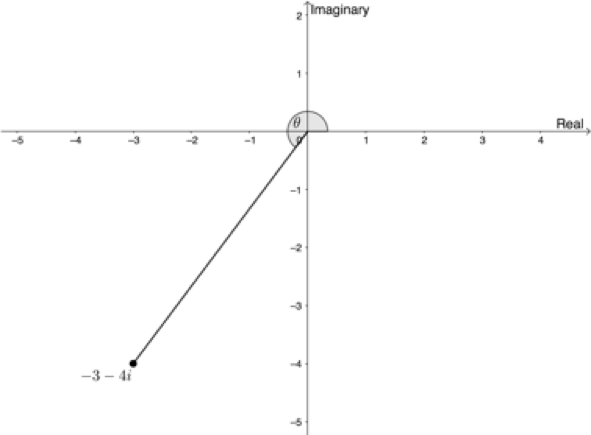
   [latex]\scriptsize \begin{align*}\left| z \right| & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{{(-3)}}^{2}}+{{{(-4)}}^{2}}}}\\ & =\sqrt{{9+16}}\\ & =\sqrt{{25}}\\ & =5\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{{-4}}{5}\\\therefore \theta & ={{180}^\circ}+{{53.130}^\circ}={{233.13}^\circ}\end{align*}[/latex]

Back to Exercise 2.3

Unit 2: Assessment

1. [latex]\scriptsize z=\sqrt{2}-i[/latex]
   
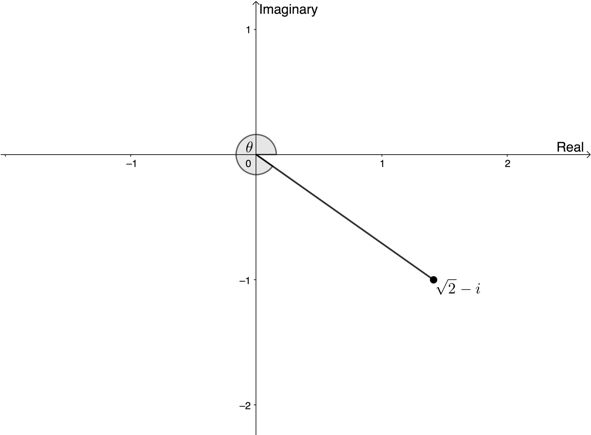
   [latex]\scriptsize \begin{align*}\left| z \right| & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{{(\sqrt{2})}}^{2}}+{{{(-1)}}^{2}}}}\\ & =\sqrt{{2+1}}\\ & =\sqrt{3}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{{-1}}{{\sqrt{3}}}\\\therefore \theta & =-{{35.26}^\circ}\quad \text{or}\quad \theta ={{360}^\circ}-{{35.26}^\circ}={{324.74}^\circ}\end{align*}[/latex]
2. [latex]\scriptsize z=5+12i[/latex]
   
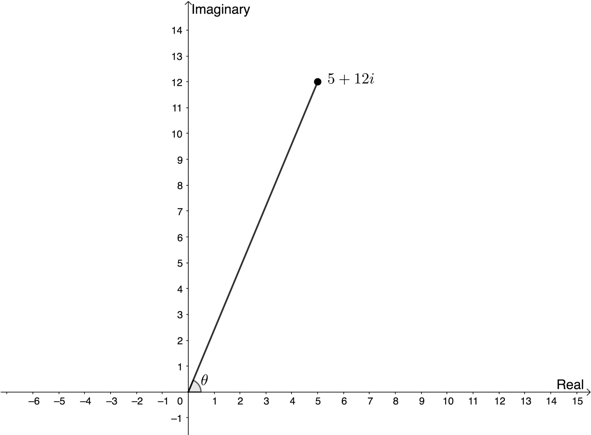
   [latex]\scriptsize \begin{align*}\left| z \right| & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{{(5)}}^{2}}+{{{(12)}}^{2}}}}\\ & =\sqrt{{25+144}}\\ & =\sqrt{{169}}\\ & =13\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{{12}}{{13}}\\\therefore \theta & ={{67.38}^\circ}\end{align*}[/latex]
3. [latex]\scriptsize z=\sqrt{3}-i[/latex]
   
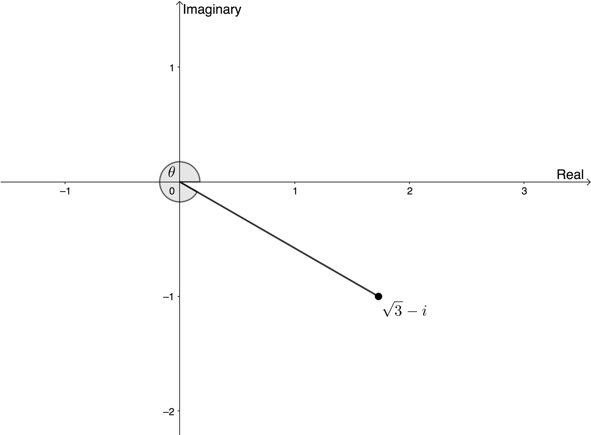
   [latex]\scriptsize \begin{align*}\left| z \right| & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{{(\sqrt{3})}}^{2}}+{{{(-1)}}^{2}}}}\\ & =\sqrt{{3+1}}\\ & =\sqrt{4}\\ & =2\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{{-1}}{2}\\\therefore \theta & =-{{30}^\circ}\quad or\quad \theta ={{360}^\circ}-{{30}^\circ}={{330}^\circ}\end{align*}[/latex]

Back to Unit 2: Assessment