Unit outcomes

By the end of this unit you will be able to:

• Use the quotient identity [latex]\scriptsize \tan \theta =\displaystyle \frac{{\sin \theta }}{{\cos \theta }}[/latex] to prove equations and simplify expressions.
• Use the square identity [latex]\scriptsize {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1[/latex] to prove equations and simplify expressions.

What you should know

Before you start this unit, make sure you can:

• Define the three basic trigonometric ratios of sine, cosine and tangent.

Introduction

A mathematical identity is an equality relating one expression to another expression, such that both expressions produce the same value for all values of the variables within a certain range of validity.

An example of an algebraic identity is [latex]\scriptsize {{(a+b)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}[/latex]. This might not seem important or meaningful. However, identities can become very important when one is trying to prove that some, possibly unrelated, thing is true. Once an identity is established, it can be used again and again without having to be proven each time. Mathematical identities, therefore, behave as reusable statements of truth.

There are many different trigonometric identities. A statement such as [latex]\scriptsize \cos ({{90}^\circ}+\theta )=-\sin \theta[/latex] can be considered a trig identity. Once we have shown it to be true once, we can simply assume that it is true in other circumstances.

There are two very important identities that you need to know about and that we will cover in this unit. These are the quotient identity and the square identity.

The quotient and square identities

The quotient and square identities are very easy to prove. We will prove each of them in turn and then see how we can use these identities to help us simplify more complicated expressions.

The quotient identity

Have a look at the circle, with radius [latex]\scriptsize 5[/latex], on the Cartesian plane in Figure 1. It has point [latex]\scriptsize P(4,3)[/latex] on its circumference.

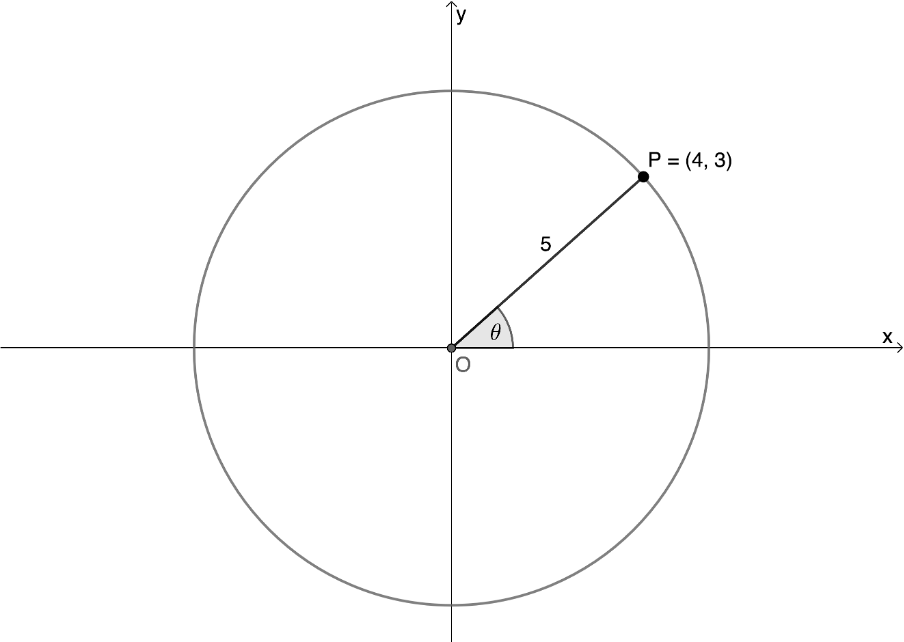
What is the value of:

• [latex]\scriptsize \sin \theta[/latex]?
• [latex]\scriptsize \cos \theta[/latex]?
• [latex]\scriptsize \tan \theta[/latex]?

Now, what is the value of [latex]\scriptsize \displaystyle \frac{{\sin \theta }}{{\cos \theta }}[/latex]?

What general statement can we write that relates [latex]\scriptsize \sin \theta[/latex], [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \tan \theta[/latex]?

In Figure 1, we know that:

• [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}=\displaystyle \frac{3}{5}[/latex]
• [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}=\displaystyle \frac{4}{5}[/latex]
• [latex]\scriptsize \tan \theta =\displaystyle \frac{y}{x}=\displaystyle \frac{3}{4}[/latex]

We can see that [latex]\scriptsize \displaystyle \frac{{\sin \theta }}{{\cos \theta }}=\displaystyle \frac{{\displaystyle \frac{y}{r}}}{{\displaystyle \frac{x}{r}}}=\displaystyle \frac{{\displaystyle \frac{3}{5}}}{{\displaystyle \frac{4}{5}}}=\displaystyle \frac{3}{5}\times \displaystyle \frac{5}{4}=\displaystyle \frac{3}{4}=\tan \theta[/latex]. The equation [latex]\scriptsize \displaystyle \frac{{\sin \theta }}{{\cos \theta }}=\tan \theta[/latex] is the quotient identity and is true for all values of [latex]\scriptsize \theta[/latex].

In general, [latex]\scriptsize \displaystyle \frac{{\sin \theta }}{{\cos \theta }}=\displaystyle \frac{{\displaystyle \frac{y}{r}}}{{\displaystyle \frac{x}{r}}}=\displaystyle \frac{y}{r}\times \displaystyle \frac{r}{x}=\displaystyle \frac{y}{x}=\tan \theta[/latex].

Now that we know that [latex]\scriptsize \displaystyle \frac{{\sin \theta }}{{\cos \theta }}=\tan \theta[/latex] is true for all values of [latex]\scriptsize \theta[/latex], we can manipulate it in various ways. We now also know that [latex]\scriptsize \sin \theta =\tan \theta \times \cos \theta[/latex] and [latex]\scriptsize \displaystyle \frac{{\sin \theta }}{{\tan \theta }}=\cos \theta[/latex].

Take note!

The quotient identity is another way to explain why the tangent function has vertical asymptotes at [latex]\scriptsize {{90}^\circ}[/latex] and [latex]\scriptsize {{270}^\circ}[/latex] (for [latex]\scriptsize {{0}^\circ}\le \theta \le {{360}^\circ}[/latex]). [latex]\scriptsize \cos {{90}^\circ}=0[/latex] and [latex]\scriptsize \cos {{270}^\circ}=0[/latex]. Therefore, at [latex]\scriptsize \theta ={{90}^\circ}[/latex] and [latex]\scriptsize \theta ={{270}^\circ}[/latex], [latex]\scriptsize \tan \theta =\displaystyle \frac{{\sin \theta }}{{\cos \theta }}[/latex] is undefined.

The square identity

Let’s use the same circle in Figure 1 to prove the square identity. What is the value of:

• [latex]\scriptsize {{\sin }^{2}}\theta[/latex]
• [latex]\scriptsize {{\cos }^{2}}\theta[/latex]
• [latex]\scriptsize {{\sin }^{2}}\theta +{{\cos }^{2}}\theta[/latex]?

Can you prove that [latex]\scriptsize {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1[/latex] is always true? Try this before you read on.

Here is the general proof:
[latex]\scriptsize \begin{align*}{{\sin }^{2}}\theta +{{\cos }^{2}}\theta&={{\left( {\displaystyle \frac{y}{r}} \right)}^{2}}+{{\left( {\displaystyle \frac{x}{r}} \right)}^{2}}\\&=\displaystyle \frac{{{{y}^{2}}}}{{{{r}^{2}}}}+\displaystyle \frac{{{{x}^{2}}}}{{{{r}^{2}}}}\\&=\displaystyle \frac{{{{y}^{2}}+{{x}^{2}}}}{{{{r}^{2}}}}&& \text{But }{{x}^{2}}+{{y}^{2}}={{r}^{2}}\text{ by Pythagoras}\\&= \displaystyle \frac{{{{r}^{2}}}}{{{{r}^{2}}}}\\&=1\end{align*}[/latex]

We can manipulate the square identity to get the following, which are also useful:

• [latex]\scriptsize {{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta[/latex]
• [latex]\scriptsize \sin \theta =\pm \sqrt{{1-{{{\cos }}^{2}}\theta }}[/latex] (the sign depends on which quadrant the angle is in)
• [latex]\scriptsize {{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta[/latex]
• [latex]\scriptsize \cos \theta =\pm \sqrt{{1-{{{\sin }}^{2}}\theta }}[/latex] (the sign depends on which quadrant the angle is in)

Using the quotient and square identities

We use the quotient and square identities to solve equations, simplify complicated expressions or prove other identities. Doing this can take some practise. The more you practise the better you will get at it.

Example 3.1

Simplify [latex]\scriptsize {{\tan }^{2}}\theta \times {{\cos }^{2}}\theta[/latex].

Solution

Whenever you see tangent, it is usually a good idea to use the quotient identity to replace this with [latex]\scriptsize \displaystyle \frac{{\sin \theta }}{{\cos \theta }}[/latex].

[latex]\scriptsize \begin{align*}{{\tan }^{2}}\theta \times {{\cos }^{2}}\theta &={{\left( {\tan \theta } \right)}^{2}}\times {{\cos }^{2}}\theta&&\text{Remember }{{\tan }^{2}}\theta=\tan \theta \times \tan \theta\\ &={{\left( {\displaystyle \frac{{\sin \theta }}{{\cos \theta }}} \right)}^{2}}\times {{\cos }^{2}}\theta \\&=\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{\bcancel{{{{{\cos }}^{2}}\theta }}}}\times \displaystyle \frac{{\bcancel{{{{{\cos }}^{2}}\theta }}}}{1}\\&={{\sin }^{2}}\theta \end{align*}[/latex]

We could use the square identity to replace [latex]\scriptsize {{\sin }^{2}}\theta[/latex] with [latex]\scriptsize 1-{{\cos }^{2}}\theta[/latex] but this would be a more complicated expression.

Example 3.2

Simplify [latex]\scriptsize \displaystyle \frac{1}{{{{{\cos }}^{2}}\theta }}-{{\tan }^{2}}\theta[/latex].

Solution

Start by using the quotient identity to replace [latex]\scriptsize {{\tan }^{2}}\theta[/latex].
[latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{{\cos }}^{2}}\theta }}-{{\tan }^{2}}\theta&=\displaystyle \frac{1}{{{{{\cos }}^{2}}\theta }}-\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}\\&=\displaystyle \frac{{1-{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}\end{align*}[/latex]

Now we have an expression in the numerator that can be simplified using the square identity.
[latex]\scriptsize \begin{align*}{{\sin }^{2}}\theta +{{\cos }^{2}}\theta & =1\\\therefore {{\cos }^{2}}\theta & =1-{{\sin }^{2}}\theta \end{align*}[/latex]

[latex]\scriptsize \begin{align*}\displaystyle \frac{{1-{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}&=\displaystyle \frac{{{{{\cos }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}\\&=1\end{align*}[/latex]

Example 3.3

Prove that [latex]\scriptsize \displaystyle \frac{{\cos x}}{{1+\sin x}}=\displaystyle \frac{{1-\sin x}}{{\cos x}}[/latex].

Solution

This is a different kind of question to Examples 3.1 and 3.2. Here we need to prove that the given left-hand side (LHS) is equal to the given right-hand side (RHS). We can either simplify one side to be exactly the same as the other or we can simplify both sides to the exact same expression. In either case, start with one side of the equality and simplify it as far as possible to see where this gets you.

[latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{{\cos x}}{{1+\sin x}}\\&=\displaystyle \frac{{\cos x}}{{1+\sin x}}\times \displaystyle \frac{{1-\sin x}}{{1-\sin x}}\end{align*}[/latex]

Multiplying the fraction by this convenient form of [latex]\scriptsize 1[/latex] means that we can create a difference of two squares [latex]\scriptsize (1+\sin x)(1-\sin x)[/latex] in the denominator which will give us [latex]\scriptsize 1-{{\sin }^{2}}x[/latex]. So now we can use the square identity.
[latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{{\cos x}}{{1+\sin x}}\\&=\displaystyle \frac{{\cos x}}{{1+\sin x}}\times \displaystyle \frac{{1-\sin x}}{{1-\sin x}}\\&=\displaystyle \frac{{\cos x(1-\sin x)}}{{(1+\sin x)(1-\sin x)}}\\&=\displaystyle \frac{{\cos x(1-\sin x)}}{{1-{{{\sin }}^{2}}x}}\quad \left[ {{{{\sin }}^{2}}x+{{{\cos }}^{2}}=1\therefore 1-{{{\sin }}^{2}}x={{{\cos }}^{2}}x} \right]\\&=\displaystyle \frac{{\bcancel{{\cos x}}(1-\sin x)}}{{{{{\cos }}^{{\bcancel{2}}}}x}}\\&=\displaystyle \frac{{1-\sin x}}{{\cos x}}=\text{RHS}\end{align*}[/latex]

We have proven that the LHS is equal to the RHS.

Exercise 3.1

1. Reduce the following to a single trig ratio:
   1. [latex]\scriptsize \displaystyle \frac{{\sin x}}{{\tan x}}[/latex]
   2. [latex]\scriptsize 1-\cos \alpha \sin \alpha \tan \alpha[/latex]
   3. [latex]\scriptsize {{\tan }^{2}}\theta \text{co}{{\text{s}}^{2}}\theta \text{+ ta}{{\text{n}}^{2}}\theta \text{si}{{\text{n}}^{2}}\theta[/latex]
2. Prove the following identities:
   1. [latex]\scriptsize (1+\sin \text{ }x)[1+\sin (-x)]\text{ }={{\cos }^{2}}x[/latex]
   2. [latex]\scriptsize {{\cos }^{2}}\alpha (1+{{\tan }^{2}}\alpha )=1[/latex]
   3. [latex]\scriptsize \displaystyle \frac{{{{{\sin }}^{2}}\theta -1}}{{\tan \theta \sin \theta -\tan \theta }}=\displaystyle \frac{{\sin \theta +1}}{{\tan \theta }}[/latex]

The full solutions are at the end of the unit.

Using the identities to prove and/or simplify other statements does take some practise. Here are some useful strategies you can apply:

Take note!

Strategies to prove identities:

• Change all ratios to sine and cosine. Use the quotient identity to do this. Very often, you will create terms that can ‘cancel’.
• Choose the more complicated side of the equality to simplify. Often this will simplify down to the other side of the equality.
• Look out for opportunities to factorise, especially common factors, difference of squares and sometimes quadratics.
• If this does not happen, then try and simplify the other side of the equality as well.
• A square root sign or a squared term usually indicates that you need to use the square identity.
• Try replacing [latex]\scriptsize 1[/latex] with [latex]\scriptsize {{\sin }^{2}}\theta +{{\cos }^{2}}\theta[/latex].
• Try multiplying fractions by convenient forms of [latex]\scriptsize 1[/latex] such as [latex]\scriptsize \displaystyle \frac{{1+\cos \theta }}{{1+\cos \theta }}[/latex] to try and create a square identity that can be replaced with [latex]\scriptsize 1[/latex].

Summary

In this unit you have learnt the following:

• How to prove trig identities by simplifying the LHS and/or the RHS to show that the LHS of the expression is equal to the RHS of the expression.

Unit 3: Assessment

Suggested time to complete: 75 minutes

1. Simplify the following expressions down to a single trig ratio:
   1. [latex]\scriptsize \displaystyle \frac{{1-{{{\cos }}^{2}}x}}{{{{{\tan }}^{2}}x}}+2{{\sin }^{2}}x[/latex]
   2. [latex]\scriptsize \displaystyle \frac{{1-{{{\cos }}^{2}}\beta }}{{\tan \beta \sin \beta }}[/latex]
   3. [latex]\scriptsize \tan x\cos x\sin (-x)[/latex]
   4. [latex]\scriptsize \left( {\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{1-{{{\sin }}^{2}}\theta }}} \right)-{{\tan }^{2}}\theta[/latex]
2. Simplify [latex]\scriptsize \displaystyle \frac{{\cos ({{{90}}^\circ}-x)\cos ({{{360}}^\circ}-x)\tan x}}{{\sin ({{{90}}^\circ}-x)\cos ({{{180}}^\circ}-x)\tan ({{{180}}^\circ}+x)}}[/latex].
3. Prove the following identities:
   1. [latex]\scriptsize {{(\sin x+\cos x)}^{2}}=1+2\sin x\cos x[/latex]
   2. [latex]\scriptsize \cos x-{{\cos }^{3}}x=\cos x{{\sin }^{2}}x[/latex]
   3. [latex]\scriptsize \displaystyle \frac{{1+{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}=\displaystyle \frac{{2{{{\tan }}^{2}}\theta }}{{{{{\sin }}^{2}}\theta }}-1[/latex]
   4. [latex]\scriptsize \left( {\displaystyle \frac{1}{{\cos x}}+\tan x} \right)\left( {\displaystyle \frac{1}{{\cos x}}-\tan x} \right)=1[/latex]
   5. [latex]\scriptsize {{\sin }^{4}}\theta -{{\cos }^{4}}\theta =1-2{{\cos }^{2}}\theta[/latex]
   6. [latex]\scriptsize (1-{{\sin }^{2}}x)(1+{{\tan }^{2}}x)=1[/latex]
   7. [latex]\scriptsize \displaystyle \frac{{{{{\cos }}^{2}}x-{{{\sin }}^{2}}x}}{{1-{{{\tan }}^{2}}x}}={{\cos }^{2}}x[/latex]
   8. [latex]\scriptsize \displaystyle \frac{{2\sin x\cos x}}{{\sin x+\cos x}}+\displaystyle \frac{1}{{\sin x+\cos x}}=\sin x+\cos x[/latex]
   9. [latex]\scriptsize \displaystyle \frac{{{{{\cos }}^{2}}\alpha }}{{\sin \alpha }}+\cos \alpha \tan \alpha =\displaystyle \frac{1}{{\sin \alpha }}[/latex]
   10. [latex]\scriptsize \displaystyle \frac{{(1+{{{\tan }}^{2}}x)\sin x}}{{(1-\tan x)}}=\displaystyle \frac{{\tan x}}{{\cos x-\sin x}}[/latex]

The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

1. .
   1. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin x}}{{\tan x}}&=\displaystyle \frac{{\sin x}}{{\displaystyle \frac{{\sin x}}{{\cos x}}}}\\&=\displaystyle \frac{{\sin x}}{1}\times \displaystyle \frac{{\cos x}}{{\sin x}}\\&=\cos x\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}1-\cos\alpha\sin\alpha\tan\alpha&=1-\bcancel{\cos\alpha}\sin\alpha\displaystyle \frac{\sin\alpha}{\bcancel{\cos\alpha}}\\ &=1-sin^2\alpha\\ &=\cos^2\alpha \end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}{{\tan }^{2}}\theta \text{co}{{\text{s}}^{2}}\theta \text{+ ta}{{\text{n}}^{2}}\theta \text{si}{{\text{n}}^{2}}\theta &=\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}\cdot {{\cos }^{2}}\theta +\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}\cdot {{\sin }^{2}}\theta \\&=\displaystyle \frac{{{{{\sin }}^{2}}\theta \bcancel{{{{{\cos }}^{2}}\theta }}}}{{\bcancel{{{{{\cos }}^{2}}\theta }}}}+\displaystyle \frac{{{{{\sin }}^{2}}\theta {{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}\\&={{\sin }^{2}}\theta +\displaystyle \frac{{{{{\sin }}^{4}}\theta }}{{{{{\cos }}^{2}}\theta }}\\&=\displaystyle \frac{{{{{\sin }}^{2}}\theta {{{\cos }}^{2}}\theta +{{{\sin }}^{4}}\theta }}{{{{{\cos }}^{2}}\theta }}&&\text{Take a common factor of }{{\sin }^{2}}\theta \text{ out of the numerator}\\&=\displaystyle \frac{{{{{\sin }}^{2}}\theta ({{{\cos }}^{2}}\theta +{{{\sin }}^{2}}\theta )}}{{{{{\cos }}^{2}}\theta }}&& \text{Use the square identity}\\&=\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}&& \text{Use the quotient identity}\\&={{\tan }^{2}}\theta \end{align*}[/latex]
2. .
   1. .
      [latex]\scriptsize \begin{align*}\text{LHS}&=(1+\sin x)[1+\sin (-x)]\\&=(1+\sin x)(1-\sin x)\\&=1-{{\sin }^{2}}x\\&={{\cos }^{2}}x=\text{RHS}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\text{LHS}&={{\cos }^{2}}\alpha (1+{{\tan }^{2}}\alpha )\\&={{\cos }^{2}}\alpha \left( {1+\displaystyle \frac{{{{{\sin }}^{2}}\alpha }}{{{{{\cos }}^{2}}\alpha }}} \right)&& \text{Add terms in brackets over the LCD of }{{\cos }^{2}}\alpha \\&={{\cos }^{2}}\alpha \left( {\displaystyle \frac{{{{{\cos }}^{2}}\alpha +{{{\sin }}^{2}}\alpha }}{{{{{\cos }}^{2}}\alpha }}} \right)&& \text{Use the square identity}\\&={{\text{cos}}^{2}}\alpha \left( {\displaystyle \frac{1}{{{{{\cos }}^{2}}\alpha }}} \right)\\&=1=\text{RHS}\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{\sin^2\theta-1}{\tan\theta\sin\theta-\tan\theta}&&\text{Factorise the numerator (diff of squares) and denominator (common factor)}\\ &=\displaystyle \frac{(\sin\theta+1)\bcancel{(\sin\theta-1)}}{\tan\theta\bcancel{(\sin\theta-1)}}\\ &=\displaystyle \frac{\sin\theta+1}{\tan\theta} \end{align*}[/latex]

Back to Exercise 3.1

Unit 3: Assessment

1. .
   1. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{1-{{{\cos }}^{2}}x}}{{{{{\tan }}^{2}}x}}+2{{\sin }^{2}}x&=\displaystyle \frac{{{{{\sin }}^{2}}x}}{{{{{\tan }}^{2}}x}}+2{{\sin }^{2}}x\\&=\displaystyle \frac{{{{{\sin }}^{2}}x}}{{\displaystyle \frac{{{{{\sin }}^{2}}x}}{{{{{\cos }}^{2}}x}}}}+2{{\sin }^{2}}x\\&=\displaystyle \frac{{\bcancel{{{{{\sin }}^{2}}x}}}}{1}\times \displaystyle \frac{{{{{\cos }}^{2}}x}}{{\bcancel{{{{{\sin }}^{2}}x}}}}+2{{\sin }^{2}}x\\&={{\cos }^{2}}x+2{{\sin }^{2}}x\\&=1-{{\sin }^{2}}x+2{{\sin }^{2}}x\\&=1+{{\sin }^{2}}x\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{1-{{{\cos }}^{2}}\beta }}{{\tan \beta \sin \beta }}&=\displaystyle \frac{{{{{\sin }}^{{\bcancel{2}}}}\beta }}{{\tan \beta \bcancel{{\sin \beta }}}}\\&=\displaystyle \frac{{\sin \beta }}{{\tan \beta }}\quad \left[ {\displaystyle \frac{{\sin \beta }}{{\cos \beta }}=\tan \beta \therefore \displaystyle \frac{{\sin \beta }}{{\tan \beta }}=\cos \beta } \right]\\&=\cos \beta \end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}\tan x\cos x\sin (-x)&=\tan x\cos x(-\sin x)\\&=\displaystyle \frac{{\sin x}}{{\bcancel{{\cos x}}}}\cdot \bcancel{{\cos x}}\cdot (-\sin x)\\&=-{{\sin }^{2}}x\end{align*}[/latex]
   4. .
      [latex]\scriptsize \begin{align*}\left( {\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{1-{{{\sin }}^{2}}\theta }}} \right)-{{\tan }^{2}}\theta &=\left( {\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}} \right)-{{\tan }^{2}}\theta \\&={{\tan }^{2}}\theta -{{\tan }^{2}}\theta \\&=0\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{\cos ({{{90}}^\circ}-x)\cos ({{{360}}^\circ}-x)\tan x}}{{\sin ({{{90}}^\circ}-x)\cos ({{{180}}^\circ}-x)\tan ({{{180}}^\circ}+x)}}&=\displaystyle \frac{{\sin x\bcancel{{\cos x}}\bcancel{{\tan x}}}}{{\bcancel{{\cos x}}(-\cos x)\bcancel{{\tan x}}}}\\&=-\displaystyle \frac{{\sin x}}{{\cos x}}\\&=-\tan x\end{align*}[/latex]
3. .
   1. .
      [latex]\scriptsize \begin{align*}\text{LHS}&={{(\sin x+\cos x)}^{2}}\\&=(\sin x+\cos x)(\sin x+\cos x)\\&={{\sin }^{2}}x+\sin x\cos x+\sin x\cos x+{{\cos }^{2}}x\\&={{\sin }^{2}}+{{\cos }^{2}}x+2\sin x\cos x\\&=1+2\sin x\cos x=\text{RHS}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\text{LHS}&=\cos x-{{\cos }^{3}}x\\&=\cos (1-{{\cos }^{2}}x)\\&=\cos x{{\sin }^{2}}x=\text{RHS}\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{{1+{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}\\&=\displaystyle \frac{{1+(1-{{{\cos }}^{2}}\theta )}}{{{{{\cos }}^{2}}\theta }}\\&=\displaystyle \frac{{2-{{{\cos }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}\\&=\displaystyle \frac{2}{{{{{\cos }}^{2}}\theta }}-\displaystyle \frac{{{{{\cos }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}\\&=\displaystyle \frac{2}{{{{{\cos }}^{2}}\theta }}-1\\&=\displaystyle \frac{2}{{\displaystyle \frac{{{{{\sin }}^{2}}\theta }}{{{{{\tan }}^{2}}\theta }}}}-1\\&=\displaystyle \frac{2}{1}\times \displaystyle \frac{{{{{\tan }}^{2}}\theta }}{{{{{\sin }}^{2}}\theta }}-1\\&=\displaystyle \frac{{2{{{\tan }}^{2}}\theta }}{{{{{\sin }}^{2}}\theta }}-1=\text{RHS}\end{align*}[/latex]
   4. .
      [latex]\scriptsize \begin{align*}\text{LHS}&=\left( {\displaystyle \frac{1}{{\cos x}}+\tan x} \right)\left( {\displaystyle \frac{1}{{\cos x}}-\tan x} \right)\\&=\displaystyle \frac{1}{{{{{\cos }}^{2}}x}}-{{\tan }^{2}}x\\&=\displaystyle \frac{1}{{{{{\cos }}^{2}}x}}-\displaystyle \frac{{{{{\sin }}^{2}}x}}{{{{{\cos }}^{2}}x}}\\&=\displaystyle \frac{{1-{{{\sin }}^{2}}x}}{{{{{\cos }}^{2}}x}}\\&=\displaystyle \frac{{{{{\cos }}^{2}}x}}{{{{{\cos }}^{2}}x}}\\&=1=\text{RHS}\end{align*}[/latex]
   5. .
      [latex]\scriptsize \begin{align*}\text{LHS}&={{\sin }^{4}}\theta -{{\cos }^{4}}\theta \\&=({{\sin }^{2}}\theta +{{\cos }^{2}}\theta )({{\sin }^{2}}\theta -{{\cos }^{2}}\theta )\\&=({{\sin }^{2}}\theta -{{\cos }^{2}}\theta )\\&=\left( {(1-{{{\cos }}^{2}}\theta )-{{{\cos }}^{2}}\theta } \right)\\&=1-2{{\cos }^{2}}\theta =\text{RHS}\end{align*}[/latex]
   6. .
      [latex]\scriptsize \begin{align*}\text{LHS}&=(1-{{\sin }^{2}}x)(1+{{\tan }^{2}}x)\\&={{\cos }^{2}}x(1+{{\tan }^{2}}x)\\&={{\cos }^{2}}x+{{\cos }^{2}}x{{\tan }^{2}}x\\&={{\cos }^{2}}x+\bcancel{{{{{\cos }}^{2}}x}}\cdot \displaystyle \frac{{{{{\sin }}^{2}}x}}{{\bcancel{{{{{\cos }}^{2}}x}}}}\\&={{\cos }^{2}}x+{{\sin }^{2}}x\\&=1=\text{RHS}\end{align*}[/latex]
   7. .
      [latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{{{{{\cos }}^{2}}x-{{{\sin }}^{2}}x}}{{1-{{{\tan }}^{2}}x}}\\&=\displaystyle \frac{{{{{\cos }}^{2}}x-{{{\sin }}^{2}}x}}{{1-\displaystyle \frac{{{{{\sin }}^{2}}x}}{{{{{\cos }}^{2}}x}}}}\\&=\displaystyle \frac{{{{{\cos }}^{2}}x-{{{\sin }}^{2}}x}}{{\displaystyle \frac{{{{{\cos }}^{2}}x-{{{\sin }}^{2}}x}}{{{{{\cos }}^{2}}x}}}}\\&=\displaystyle \frac{{\bcancel{{{{{\cos }}^{2}}x-{{{\sin }}^{2}}x}}}}{1}\times \displaystyle \frac{{{{{\cos }}^{2}}x}}{{\bcancel{{{{{\cos }}^{2}}x-{{{\sin }}^{2}}x}}}}\\&={{\cos }^{2}}x=\text{RHS}\end{align*}[/latex]
   8. .
      [latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{{2\sin x\cos x}}{{\sin x+\cos x}}+\displaystyle \frac{1}{{\sin x+\cos x}}\\&=\displaystyle \frac{{2\sin x\cos x+1}}{{\sin x+\cos x}}\\&=\displaystyle \frac{{2\sin x\cos x+{{{\sin }}^{2}}x+{{{\cos }}^{2}}}}{{\sin x+\cos x}}\\&=\displaystyle \frac{{{{{\sin }}^{2}}x+2\sin x\cos x+{{{\cos }}^{2}}}}{{\sin x+\cos x}}\quad \text{Factorise the quadratic in the numerator}\\&=\displaystyle \frac{{{{{(\sin x+\cos x)}}^{{\bcancel{2}}}}}}{{\bcancel{{\sin x+\cos x}}}}\\&=\sin x+\cos x=\text{RHS}\end{align*}[/latex]
   9. .
      [latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{{{{{\cos }}^{2}}\alpha }}{{\sin \alpha }}+\cos \alpha \tan \alpha \\&=\displaystyle \frac{{{{{\cos }}^{2}}\alpha }}{{\sin \alpha }}+\bcancel{{\cos \alpha }}\times \displaystyle \frac{{\sin \alpha }}{{\bcancel{{\cos \alpha }}}}\\&=\displaystyle \frac{{{{{\cos }}^{2}}\alpha }}{{\sin \alpha }}+\sin \alpha \\&=\displaystyle \frac{{{{{\cos }}^{2}}\alpha +{{{\sin }}^{2}}\alpha }}{{\sin \alpha }}\\&=\displaystyle \frac{1}{{\sin \alpha }}=\text{RHS}\end{align*}[/latex]
   10. .
       [latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{{(1+{{{\tan }}^{2}}x)\sin x}}{{(1-\tan x)}}\\&=\displaystyle \frac{{\left( {1+\displaystyle \frac{{{{{\sin }}^{2}}x}}{{{{{\cos }}^{2}}x}}} \right)\sin x}}{{\left( {1-\displaystyle \frac{{\sin x}}{{\cos x}}} \right)}}\\&=\displaystyle \frac{{\left( {\displaystyle \frac{{{{{\cos }}^{2}}x+{{{\sin }}^{2}}x}}{{{{{\cos }}^{2}}x}}} \right)\sin x}}{{\left( {\displaystyle \frac{{\cos x-\sin x}}{{\cos x}}} \right)}}\\&=\displaystyle \frac{{\left( {\displaystyle \frac{1}{{{{{\cos }}^{2}}x}}} \right)\sin x}}{{\left( {\displaystyle \frac{{\cos x-\sin x}}{{\cos x}}} \right)}}\\&=\displaystyle \frac{{\sin x}}{{{{{\cos }}^{{\bcancel{2}}}}x}}\times \displaystyle \frac{{\bcancel{{\cos x}}}}{{(\cos x-\sin x)}}\\&=\displaystyle \frac{{\sin x}}{{\cos x(\cos x-\sin x)}}\\&=\displaystyle \frac{{\tan x}}{{\cos x-\sin x}}=\text{RHS}\end{align*}[/latex]

Back to Unit 3: Assessment