Unit outcomes

By the end of this unit you will be able to:

• Use the cosine rule to find the length of an unknown side of a triangle.
• Use the cosine rule to find an unknown angle of a triangle.

What you should know

Before you start this unit, make sure you can:

• State and use the area rule. Refer to unit 5 of this subject outcome if you need help with this.
• State and use the sine rule to find unknown sides and angles of triangles. Refer to unit 6 of this subject outcome if you need help with this.
• Use a calculator to calculate the sine or cosine of a given angle. Refer to level 2 subject outcome 3.6 unit 2 if you need help with this.
• Use a calculator to calculate the angle from a given ratio for sine or cosine. Refer to level 2 subject outcome 3.6 unit 2 if you need help with this.
• Solve simple equations.

Introduction

The sine rule that we learnt about in unit 6 is very powerful. With it, we can solve most triangles (find all the unknown sides and angles). However, there are some triangles that the sine rule cannot solve. Have a look at Figure 1. Can you use the sine rule to solve this triangle?

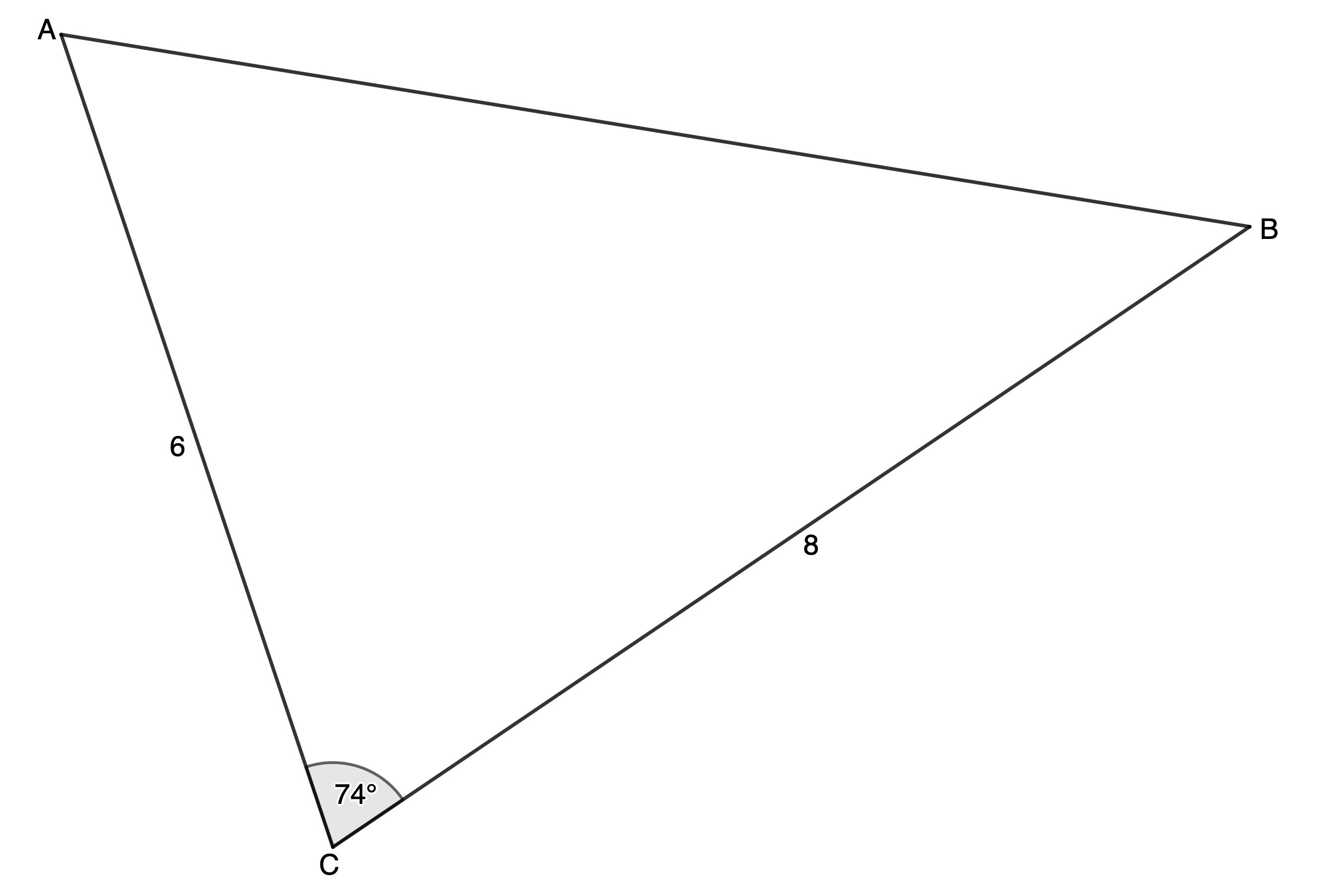
To use the sine rule we need an angle and opposite side pair. In other words, we would either need to know the length of [latex]\scriptsize AB[/latex] (side [latex]\scriptsize c[/latex]) or we would need to know the size of angle [latex]\scriptsize \hat{A}[/latex] or [latex]\scriptsize \hat{B}[/latex].

Thankfully, there is a way to solve triangles like this with another useful trig identity called the cosine rule.

The cosine rule

The cosine rule says that in any [latex]\scriptsize \Delta ABC[/latex]:

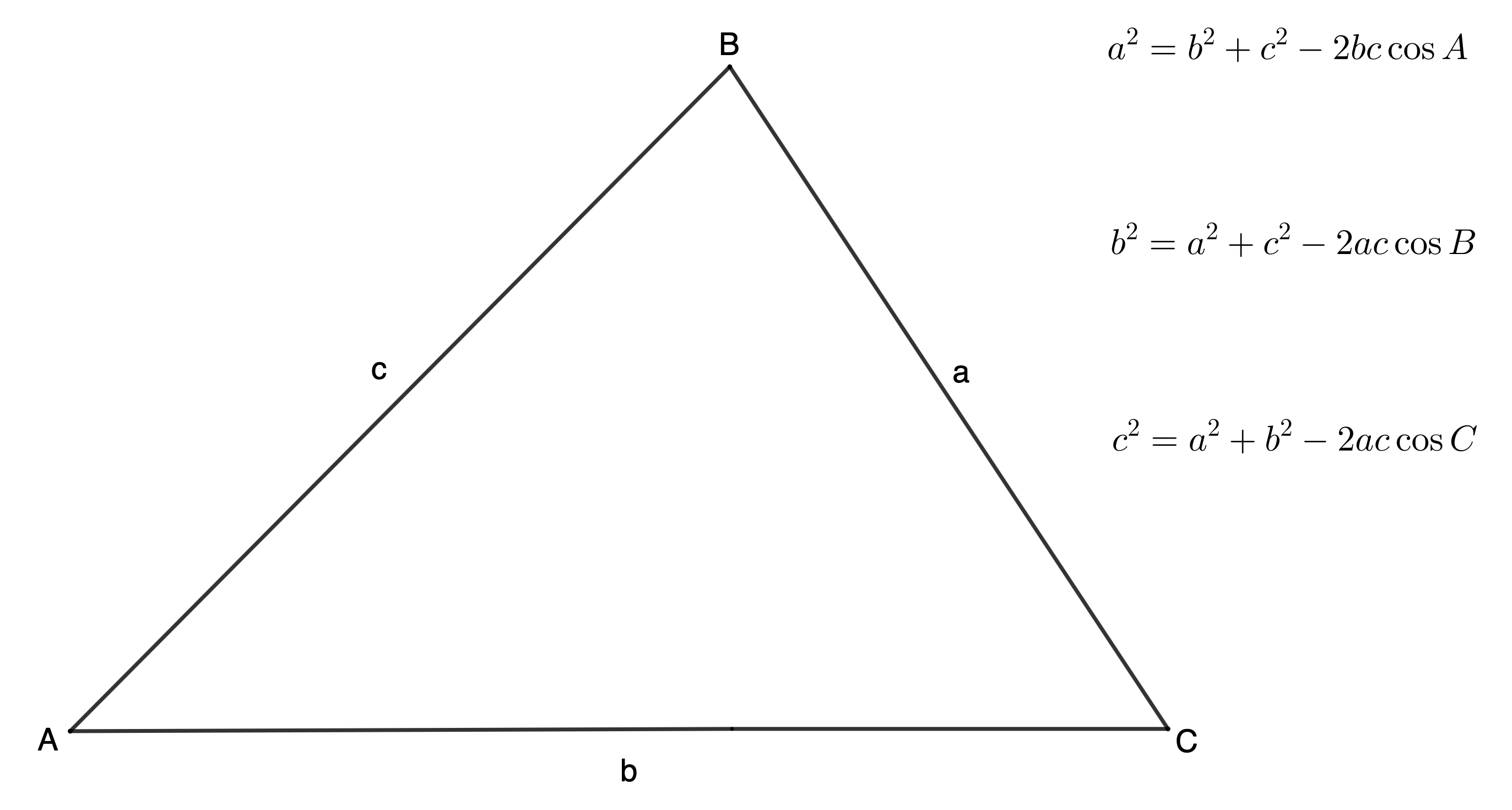
Notice two important things about the cosine rule:

• The cosine rule works when we know the lengths of any two sides and the size of the included angle.
• The side on the LHS is always the side opposite the angle of which we take the cosine.

We can use the cosine rule to work out what [latex]\scriptsize c[/latex] is in the triangle in Figure 3 because we know the lengths of two sides and the size of the included angle.

[latex]\scriptsize \begin{align*}{{c}^{2}} & ={{a}^{2}}+{{b}^{2}}-2ab\cos C\\ & ={{8}^{2}}+{{6}^{2}}-2\cdot 8\cdot 6\cdot \cos {{74}^\circ}\\\therefore c & =\sqrt{{{{8}^{2}}+{{6}^{2}}-2\cdot 8\cdot 6\cdot \cos {{{74}}^\circ}}}\\ & =8.58\end{align*}[/latex]

Because we are dealing with a physical length, we do not need to consider the negative square root.

When calculating with the cosine rule, it is important to round off only your final answer. In the calculation above, this is the sequence of keys you need to press on your Casio calculator to compute [latex]\scriptsize c[/latex].

[latex]\scriptsize \boxed{\sqrt{}}\boxed{8}\boxed{x^2}\boxed{+}\boxed{6}\boxed{x^2}\boxed{-}\boxed{2}\boxed{\times}\boxed{8}\boxed{\times}\boxed{6}\boxed{\times}\boxed{\cos}\boxed{74}\boxed{)}\boxed{=}[/latex]

Take note!

You must make sure that you get the naming of vertices and sides in your triangle correct. The side opposite vertex [latex]\scriptsize A[/latex] is [latex]\scriptsize a[/latex]. The side opposite vertex [latex]\scriptsize B[/latex] is [latex]\scriptsize b[/latex]. The side opposite vertex [latex]\scriptsize C[/latex] is [latex]\scriptsize c[/latex]. The cosine rule will only work if you label your triangle like this.

Deriving the cosine rule is a little harder than deriving either the area rule or sine rule. If you would like to know how to derive it, and you have an internet connection, watch the video “Derivation of the cosine rule”.

Because the sine rule is simpler to work with, it is advisable to use it if possible. Only if you cannot use the sine rule or you are explicitly told to use the cosine rule should you use the cosine rule.

Use the cosine rule to find an unknown side

Let’s look at an example of when you would use the cosine rule.

Example 7.1

Calculate the length of [latex]\scriptsize ST[/latex].

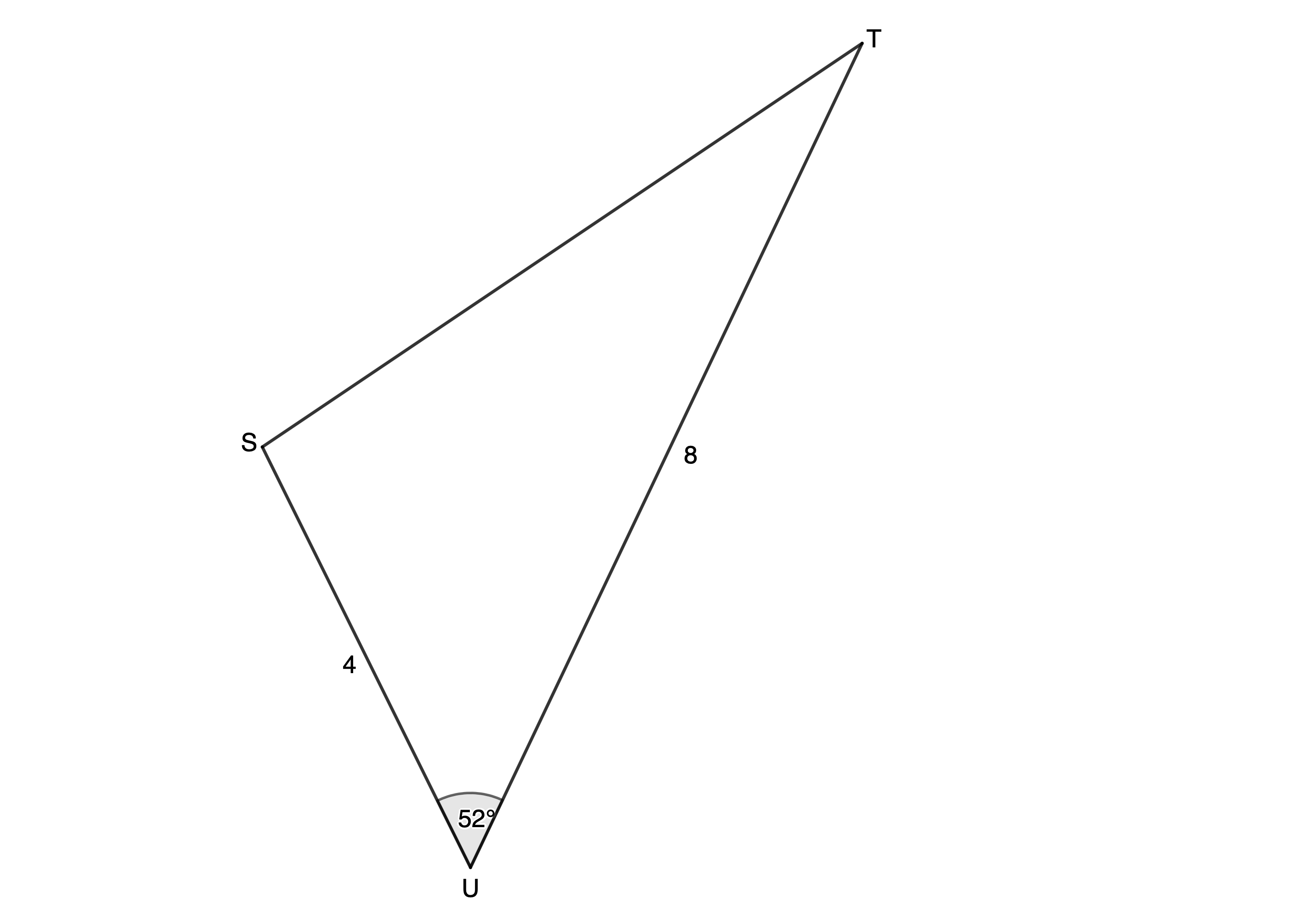
Solution

Check that we have two sides and the included angle. We know that [latex]\scriptsize ST=u[/latex] because it is opposite [latex]\scriptsize \hat{U}[/latex], and we know that [latex]\scriptsize t=4[/latex] and [latex]\scriptsize s=8[/latex].
[latex]\scriptsize \begin{align*}{{u}^{2}} & ={{s}^{2}}+{{t}^{2}}-2st\cos U\\\therefore {{u}^{2}} & ={{8}^{2}}+{{4}^{2}}-2\cdot 8\cdot 4\cdot \cos {{52}^\circ}\\\therefore u & =\sqrt{{{{8}^{2}}+{{4}^{2}}-2\cdot 8\cdot 4\cdot \cos {{{52}}^\circ}}}\\ & =6.37\end{align*}[/latex]

Exercise 7.1

1. Find the length of [latex]\scriptsize DE[/latex] in [latex]\scriptsize \Delta DEF[/latex].
   
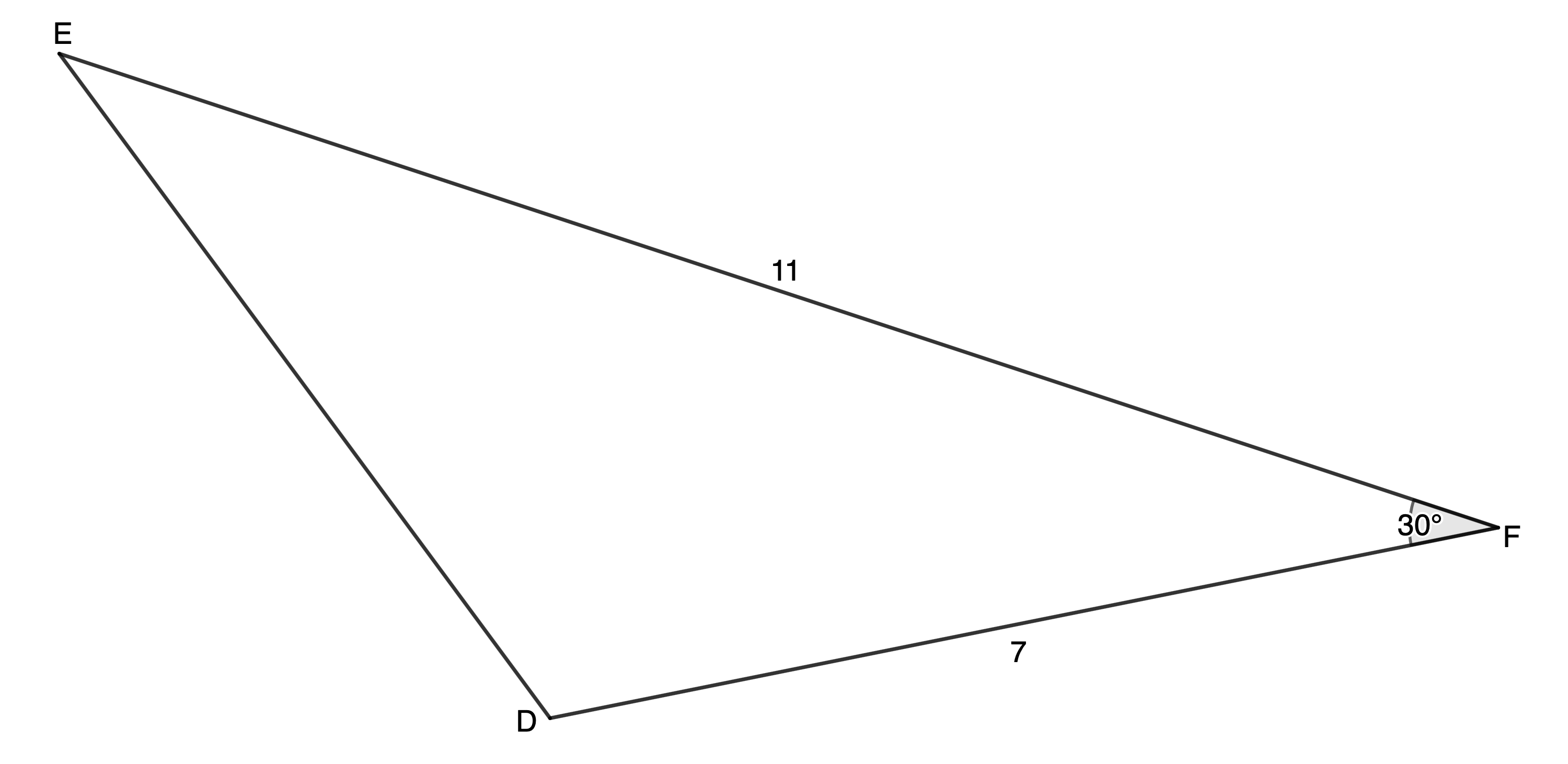
2. Find the length of [latex]\scriptsize HK[/latex].
   

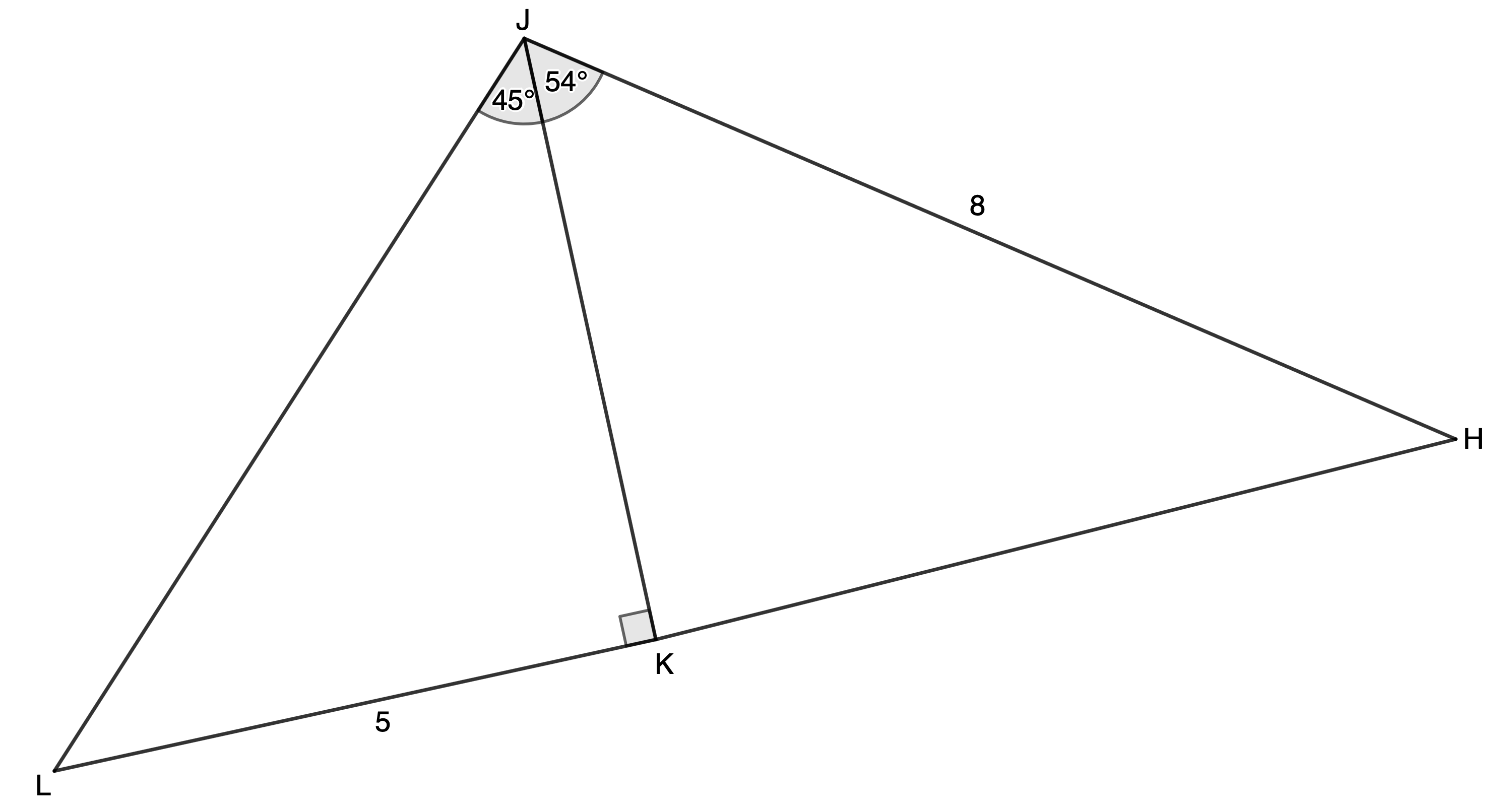
The full solutions are at the end of the unit.

Use the cosine rule to find an unknown angle

If we know the length of all three sides of a triangle, we can rearrange the cosine rule to solve for any of the unknown angles.

[latex]\scriptsize \begin{align*}{{a}^{2}} & ={{b}^{2}}+{{c}^{2}}-2bc\cos A\\\therefore {{a}^{2}}-{{b}^{2}}-{{c}^{2}} & =-2bc\cos A\\\therefore \displaystyle \frac{{{{a}^{2}}-{{b}^{2}}-{{c}^{2}}}}{{-2bc}} & =\cos A\\\therefore \cos A & =\displaystyle \frac{{-(-{{a}^{2}}+{{b}^{2}}+{{c}^{2}})}}{{-2bc}}\\ & =\displaystyle \frac{{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}}{{2bc}}\end{align*}[/latex]
Just remember the side [latex]\scriptsize a[/latex] is opposite angle [latex]\scriptsize \hat{A}[/latex], etc.

Example 7.2

Solve the following triangle:

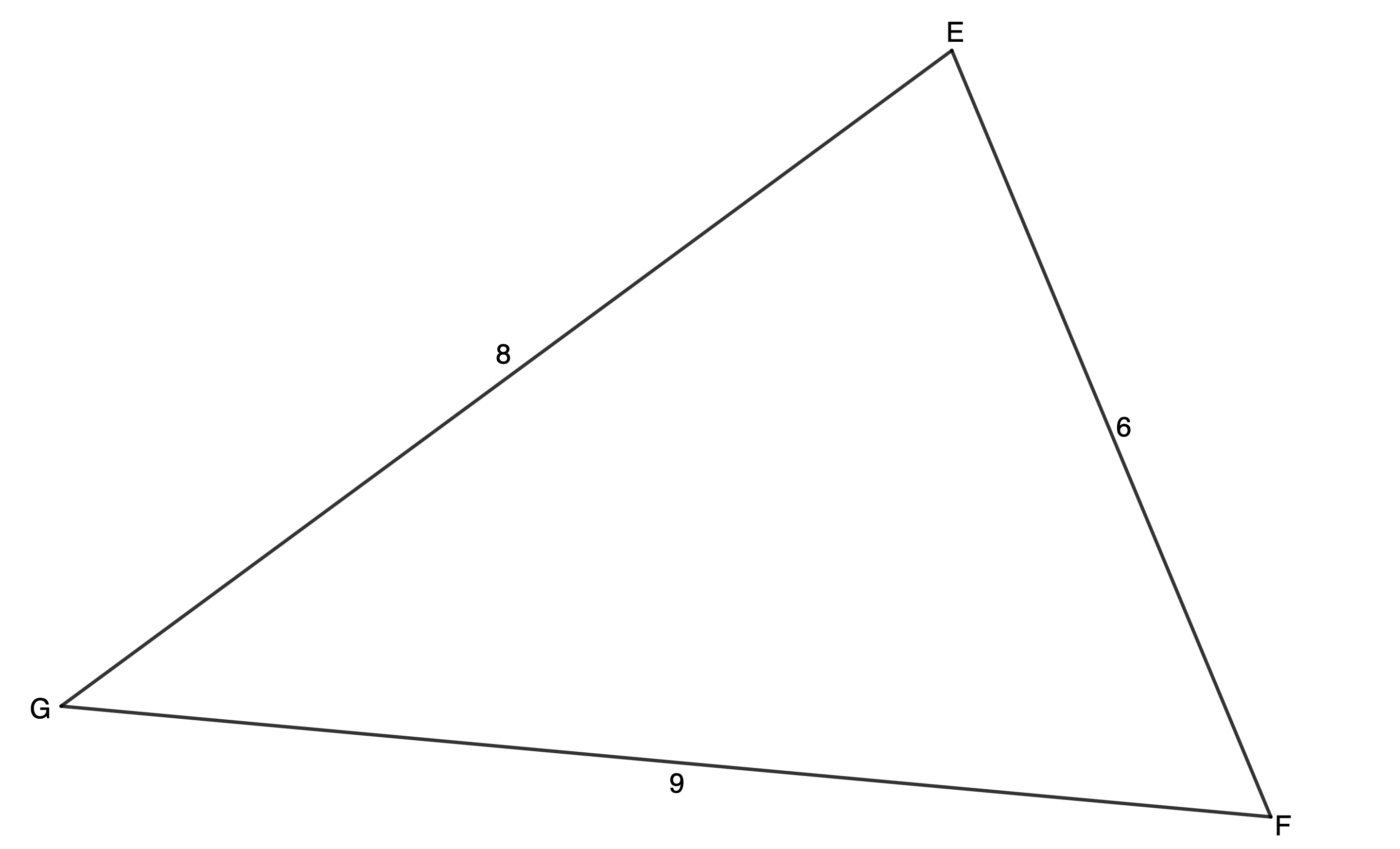
Solution

Because we have been given three sides, we know we need to use the cosine rule. We can solve for any of the unknown angles but must make sure that we arrange the three sides in the equation correctly.

We will solve for [latex]\scriptsize \hat{E}[/latex] first.
[latex]\scriptsize \begin{align*}{{e}^{2}} & ={{f}^{2}}+{{g}^{2}}-2fg\cos E\\\therefore \cos E & =\displaystyle \frac{{{{f}^{2}}+{{g}^{2}}-{{e}^{2}}}}{{2fg}}\\&=\displaystyle \frac{{{{8}^{2}}+{{6}^{2}}-{{9}^{2}}}}{{2\cdot 8\cdot 6}}\\&=0.1979\\\therefore \hat{E} & ={{78.58}^\circ}\end{align*}[/latex]
Note: Make sure that you round off only your final answer.

Now that we have a side/angle pair, we can complete solving, using the sine rule.
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin F}}{f} & =\displaystyle \frac{{\sin E}}{e}\\\therefore \displaystyle \frac{{\sin F}}{8} & =\displaystyle \frac{{\sin {{{78.58}}^\circ}}}{9}\\\therefore \sin F & =\displaystyle \frac{{8\sin {{{78.58}}^\circ}}}{9}\\\therefore F & ={{60.61}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin G}}{g} & =\displaystyle \frac{{\sin E}}{e}\\\therefore \displaystyle \frac{{\sin G}}{6} & =\displaystyle \frac{{\sin {{{78.58}}^\circ}}}{9}\\\therefore \sin G & =\displaystyle \frac{{6\sin {{{78.58}}^\circ}}}{9}\\\therefore G & ={{40.80}^\circ}\end{align*}[/latex]

Exercise 7.2

1. Solve the following triangles:
   1. [latex]\scriptsize \Delta PQR[/latex] where [latex]\scriptsize \hat{P}={{58}^\circ}[/latex], [latex]\scriptsize q=9\ \text{cm}[/latex] and [latex]\scriptsize r=7\ \text{cm}[/latex].
   2. [latex]\scriptsize \Delta LMN[/latex] where [latex]\scriptsize l=8.1[/latex], [latex]\scriptsize m=3.8[/latex] and [latex]\scriptsize n=10.3[/latex].
2. Determine the largest angle in [latex]\scriptsize \Delta JHK[/latex] where [latex]\scriptsize HJ=6[/latex], [latex]\scriptsize JK=5[/latex] and [latex]\scriptsize KH=9[/latex].

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to use the cosine rule to find the length of a side of a triangle.
• How to use the cosine rule to find the size of an angle of a triangle.

Unit 7: Assessment

Suggested time to complete: 30 minutes

Question 1 is adapted from NC(V) Mathematics Paper 2 March 2013 question 2.4

1. The sketch below shows a side view of a house. [latex]\scriptsize AB=6\ \text{m}[/latex], [latex]\scriptsize BC=5\ \text{m}[/latex], [latex]\scriptsize CD=10\ \text{m}[/latex] and [latex]\scriptsize A\hat{B}E={{49}^\circ}[/latex].
   
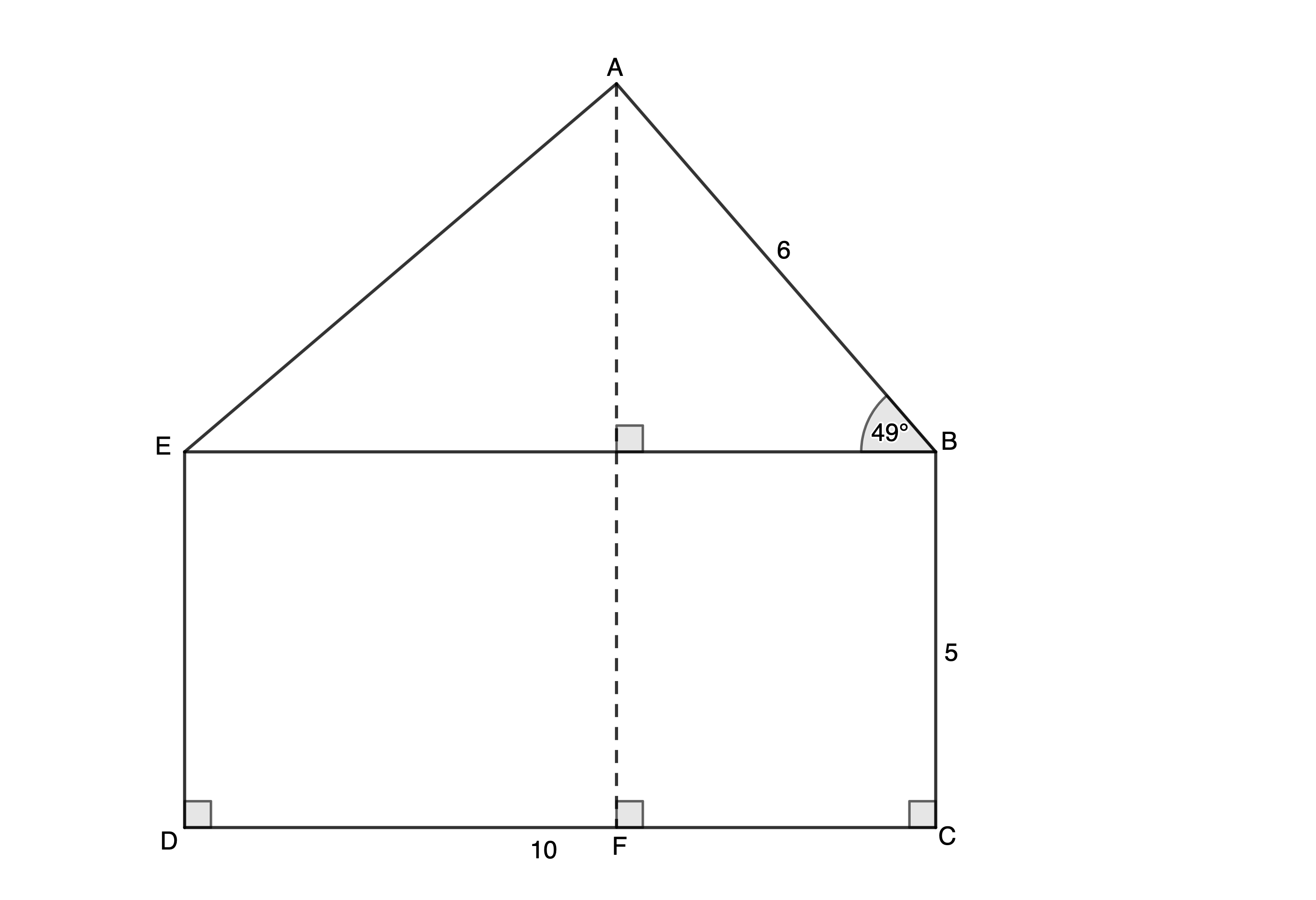
   1. Determine the length of [latex]\scriptsize AE[/latex].
   2. Calculate the magnitude of [latex]\scriptsize A\hat{E}B[/latex].
   3. Calculate the area of [latex]\scriptsize \Delta ABE[/latex].
   4. Determine the length of [latex]\scriptsize AF[/latex].
2. [latex]\scriptsize WXYZ[/latex] is a trapezium, [latex]\scriptsize WX\parallel YZ[/latex] with [latex]\scriptsize WX=8.6\ \text{m}[/latex], [latex]\scriptsize XY=2.6\ \text{m}[/latex], [latex]\scriptsize ZW=5.2\ \text{m}[/latex] and [latex]\scriptsize \hat{W}={{30}^\circ}[/latex].
   
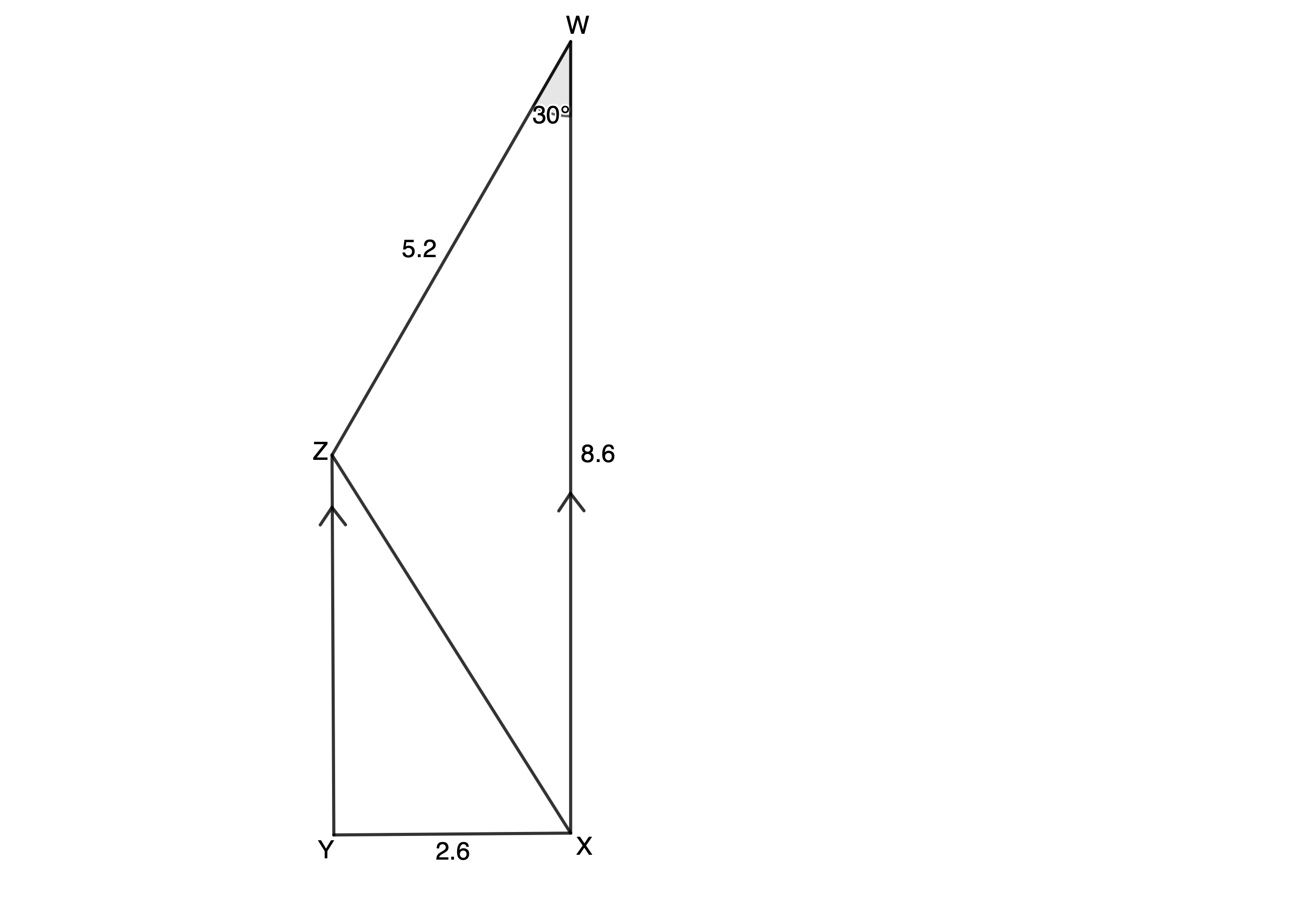
   1. Determine [latex]\scriptsize XZ[/latex].
   2. If [latex]\scriptsize W\hat{Z}X={{117.7}^\circ}[/latex], determine [latex]\scriptsize \hat{Y}[/latex].
   3. Determine area of [latex]\scriptsize WXYZ[/latex].

The full solutions are at the end of the unit.

Unit 7: Solutions

Exercise 7.1

1. We have the length of two sides and the included angle. Therefore, we can use the cosine rule.
   [latex]\scriptsize DE=f[/latex], [latex]\scriptsize FD=e=7[/latex], [latex]\scriptsize EF=d=11[/latex]
   [latex]\scriptsize \begin{align*}{{f}^{2}} & ={{d}^{2}}+{{e}^{2}}-2de\cos F\\\therefore {{f}^{2}} & ={{7}^{2}}+{{11}^{2}}-2\cdot 7\cdot 11\cdot \cos {{30}^\circ}\\\therefore f & =\sqrt{{{{7}^{2}}+{{{11}}^{2}}-2\cdot 7\cdot 11\cdot \cos {{{30}}^\circ}}}\\ & =6.05\end{align*}[/latex]
2. We do not yet have enough information to use the sine or cosine rules in [latex]\scriptsize \Delta HJK[/latex].
   In [latex]\scriptsize \Delta KJL[/latex]:
   [latex]\scriptsize \begin{align*}\tan {{45}^\circ} & =\displaystyle \frac{{LK}}{{KJ}}\\\therefore KJ & =\displaystyle \frac{{LK}}{{\tan {{{45}}^\circ}}}=\displaystyle \frac{5}{1}=5\end{align*}[/latex]
   .
   In [latex]\scriptsize \Delta HJK[/latex]:
   We know the length of two sides ([latex]\scriptsize HJ[/latex] and [latex]\scriptsize JK[/latex]) and the included angle. Therefore, we can use the cosine rule to find [latex]\scriptsize HK[/latex].
   [latex]\scriptsize \begin{align*}H{{K}^{2}} & =H{{J}^{2}}+J{{K}^{2}}-2HJ\cdot JK\cdot \cos H\hat{J}K\\\therefore H{{K}^{2}} & ={{8}^{2}}+{{5}^{2}}-2\cdot 8\cdot 5\cdot \cos {{54}^\circ}\\\therefore HK & =\sqrt{{{{8}^{2}}+{{5}^{2}}-2\cdot 8\cdot 5\cdot \cos {{{54}}^\circ}}}\\ & =6.48\end{align*}[/latex]

Back to Exercise 7.1

Exercise 7.2

1. .
   1. Make a sketch of the triangle with the given information.
      
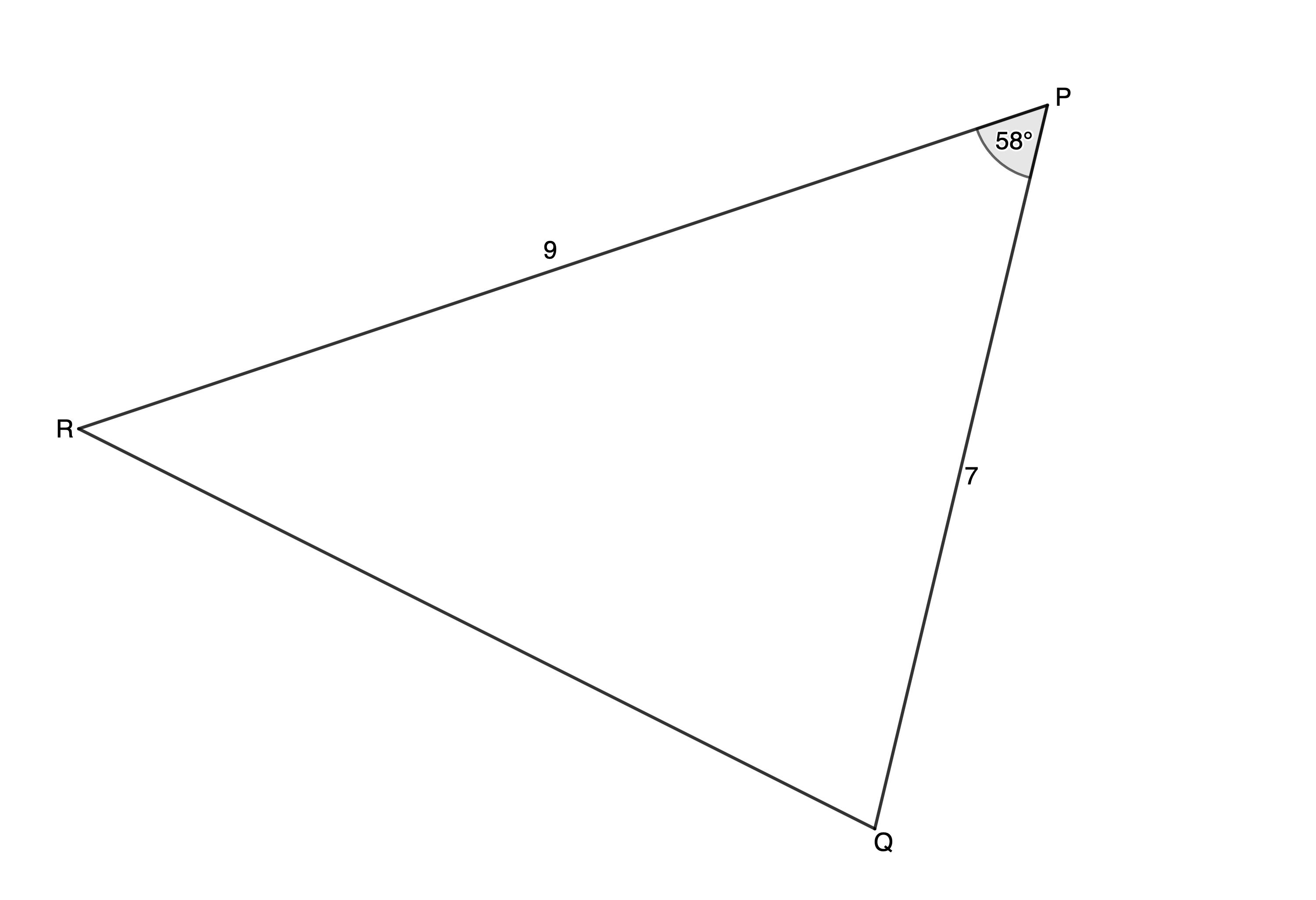
      We can use the cosine rule to find [latex]\scriptsize QR[/latex] (side [latex]\scriptsize p[/latex]).
      [latex]\scriptsize \begin{align*}Q{{R}^{2}} & =P{{Q}^{2}}+R{{P}^{2}}-2\cdot PQ\cdot RP\cdot \cos P\\\therefore Q{{R}^{2}} & ={{7}^{2}}+{{9}^{2}}-2\cdot 7\cdot 9\cdot \cos {{58}^\circ}\\\therefore QR & =\sqrt{{{{7}^{2}}+{{9}^{2}}-2\cdot 7\cdot 9\cdot \cos {{{58}}^\circ}}}\\ & =7.95\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin R}}{{PQ}} & =\displaystyle \frac{{\sin P}}{{QR}}\\\therefore \displaystyle \frac{{\sin R}}{7} & =\displaystyle \frac{{\sin {{{58}}^\circ}}}{{7.95}}\\\therefore \sin R & =\displaystyle \frac{{7\sin {{{58}}^\circ}}}{{7.95}}\\\therefore R & ={{48.31}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}\hat{Q}&={{180}^\circ}-\hat{P}-\hat{R}&&\text{(angles in a triangle are supplementary)}\\ &={{180}^\circ}-{{58}^\circ}-{{48.31}^\circ}\\ &={{73.69}^\circ}\end{align*}[/latex]
   2. Make a sketch of the triangle with the given information.
      
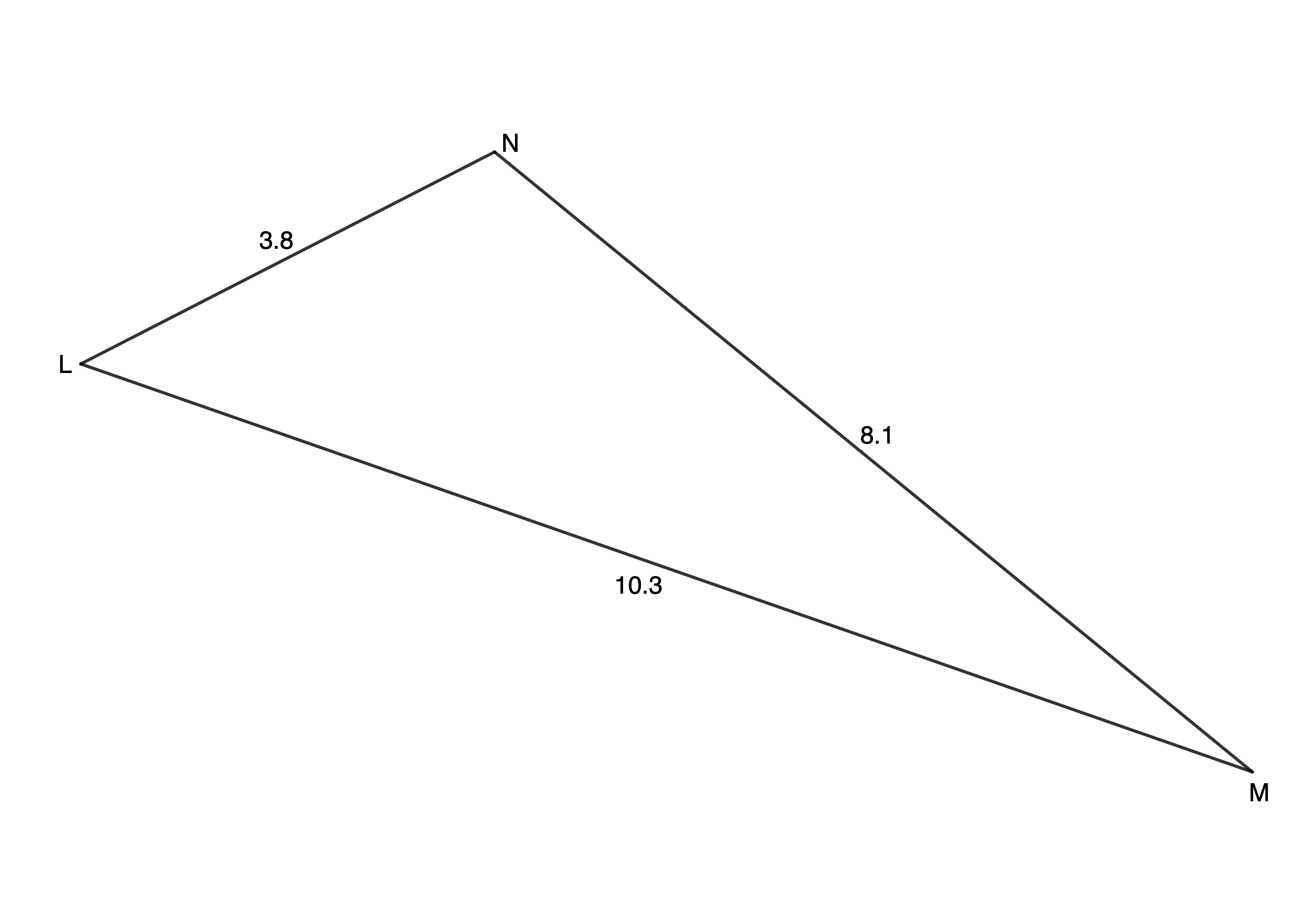
      Given three sides, we use the cosine rule to find any of the angles.[latex]\scriptsize \begin{align*}M{{N}^{2}} & =L{{M}^{2}}+N{{L}^{2}}-2\cdot LM\cdot NL\cdot \cos L\\\therefore \cos L & =\displaystyle \frac{{L{{M}^{2}}+N{{L}^{2}}-M{{N}^{2}}}}{{2\cdot LM\cdot NL}}\\\therefore \cos L & =\displaystyle \frac{{{{{10.3}}^{2}}+{{{3.8}}^{2}}-{{{8.1}}^{2}}}}{{2\cdot (10.3)\cdot (3.8)}}\\\therefore \hat{L} & ={{45.45}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin M}}{{NL}} & =\displaystyle \frac{{\sin L}}{{MN}}\\\therefore \displaystyle \frac{{\sin M}}{{3.8}} & =\displaystyle \frac{{\sin {{{45.45}}^\circ}}}{{8.1}}\\\therefore \sin M & =\displaystyle \frac{{3.8\sin {{{45.45}}^\circ}}}{{8.1}}\\\therefore \hat{M} & ={{19.53}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}\hat{N}&={{180}^\circ}-\hat{L}-\hat{M}&&\text{(angles in a triangle are supplementary)}\\&={{180}^\circ}-{{45.45}^\circ}-{{19.53}^\circ}\\&={{115.02}^\circ}\end{align*}[/latex]
2. Make a sketch of the triangle with the given information.
   
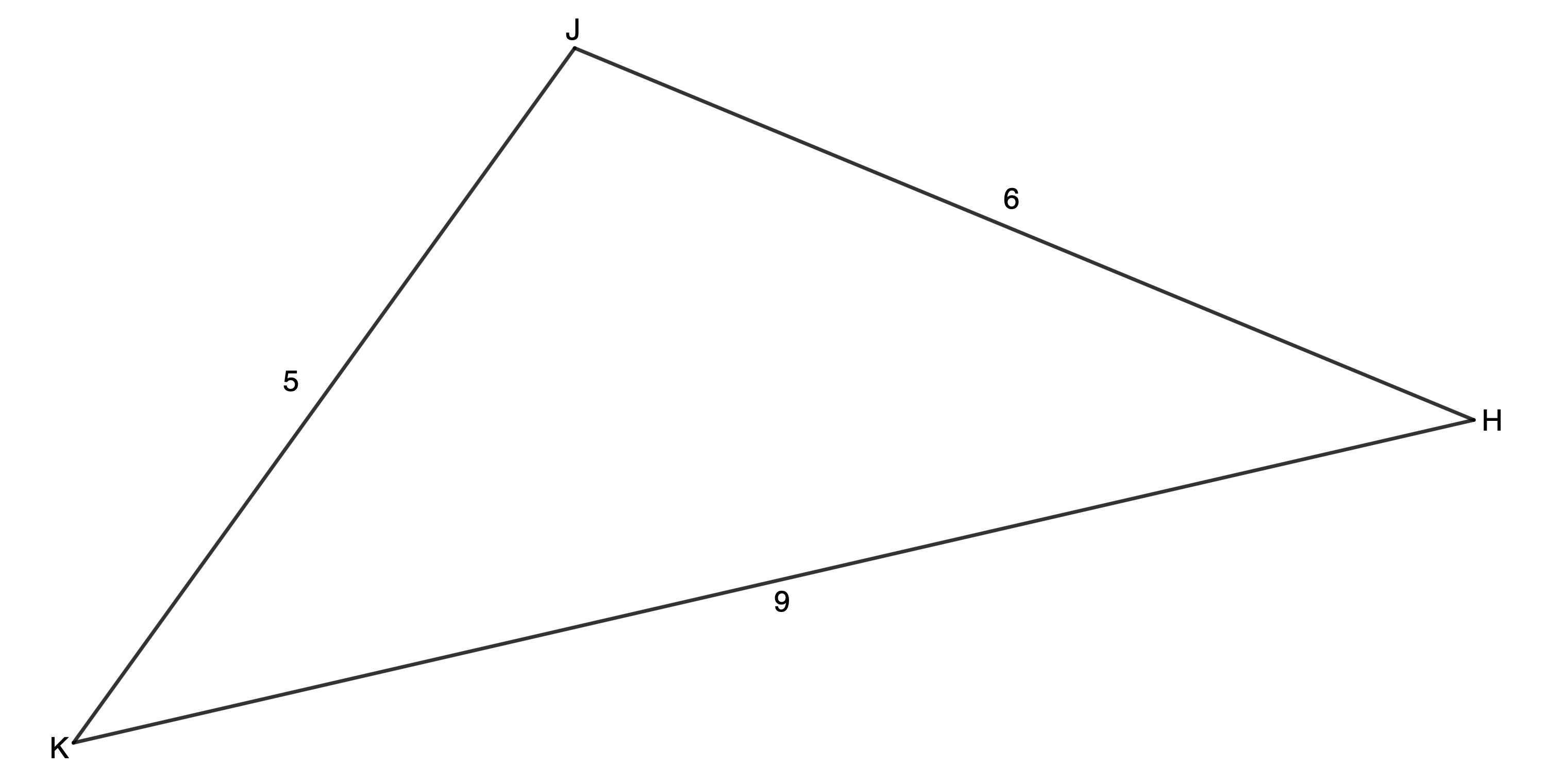
   The largest angle is the angle opposite the longest side. Therefore, [latex]\scriptsize \hat{J}[/latex] is the largest angle.
   [latex]\scriptsize \begin{align*}K{{H}^{2}} & =H{{J}^{2}}+J{{K}^{2}}-2\cdot HJ\cdot JK\cdot \cos J\\\therefore \cos J & =\displaystyle \frac{{H{{J}^{2}}+J{{K}^{2}}-K{{H}^{2}}}}{{2\cdot HJ\cdot JK}}\\\therefore \cos J & =\displaystyle \frac{{{{6}^{2}}+{{5}^{2}}-{{9}^{2}}}}{{2\cdot 6\cdot 5}}\\\therefore \hat{J} & ={{109.47}^\circ}\end{align*}[/latex]

Back to Exercise 7.2

Unit 7: Assessment

1. .
   1. [latex]\scriptsize CD\parallel EB[/latex] (corresponding angles are equal)
      [latex]\scriptsize BC\parallel ED[/latex] (co-interior angles are supplementary)
      [latex]\scriptsize \therefore BCDE[/latex] is a rectangle (both pairs of opposite sides are parallel and interior angles equal to [latex]\scriptsize {{90}^\circ}[/latex])
      [latex]\scriptsize \therefore CD=EB=10\ \text{m}[/latex] (opposite sides of a rectangle are equal)
      .
      [latex]\scriptsize \begin{align*}A{{E}^{2}} & =A{{B}^{2}}+B{{E}^{2}}-2\cdot AB\cdot BE\cdot \cos A\hat{B}E\\\therefore A{{E}^{2}} & ={{6}^{2}}+{{10}^{2}}-2\cdot 6\cdot 10\cdot \cos {{49}^\circ}\\\therefore AE & =\sqrt{{{{6}^{2}}+{{{10}}^{2}}-2\cdot 6\cdot 10\cdot \cos {{{49}}^\circ}}}\\ & =7.57\ \text{m}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin A\hat{E}B}}{{AB}} & =\displaystyle \frac{{\sin A\hat{B}E}}{{AE}}\\\therefore \displaystyle \frac{{\sin A\hat{E}B}}{6} & =\displaystyle \frac{{\sin {{{49}}^\circ}}}{{7.57}}\\\therefore \sin A\hat{E}B & =\displaystyle \frac{{6\sin {{{49}}^\circ}}}{{7.57}}\\\therefore A\hat{E}B & ={{36.74}^\circ}\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}\text{Area }\Delta ABE&=\displaystyle \frac{1}{2}\cdot AB\cdot EB\cdot \sin A\hat{B}E\\&=\displaystyle \frac{1}{2}\cdot 6\cdot 10\cdot \sin {{49}^\circ}\\&=22.64\ {{\text{m}}^{2}}\end{align*}[/latex]
   4. Let [latex]\scriptsize AF[/latex] intersect [latex]\scriptsize BE[/latex] at [latex]\scriptsize G[/latex]. Then [latex]\scriptsize AF=AG+GF[/latex].
      [latex]\scriptsize GF=BC=5\ \text{m}[/latex] (opposites sides of a rectangle are equal)
      [latex]\scriptsize AG[/latex] is the perpendicular height of [latex]\scriptsize \Delta ABE[/latex] and area [latex]\scriptsize \Delta ABE=22.64\ {{\text{m}}^{2}}[/latex].
      [latex]\scriptsize \begin{align*}\text{Area }\Delta ABE & =\displaystyle \frac{1}{2}\times b\times h\\&=\displaystyle \frac{1}{2}\times EB\times AG\\\therefore AG & =\displaystyle \frac{{2\times \text{Area }\Delta ABE}}{{EB}}\\&=\displaystyle \frac{{2\times 22.64}}{{10}}\\&=4.53\ \text{m}\end{align*}[/latex]
      Therefore [latex]\scriptsize AF=4.53+5=9.53\ \text{m}[/latex]
2. .
   1. .
      [latex]\scriptsize \begin{align*}X{{Z}^{2}} & =W{{Z}^{2}}+W{{X}^{2}}-2\cdot WZ\cdot WX\cdot \cos W\\\therefore X{{Z}^{2}} & ={{5.2}^{2}}+{{8.6}^{2}}-2\cdot (5.2)\cdot (8.6)\cdot \cos {{30}^\circ}\\\therefore XZ & =\sqrt{{{{{5.2}}^{2}}+{{{8.6}}^{2}}-2\cdot (5.2)\cdot (8.6)\cdot \cos {{{30}}^\circ}}}\\ & =4.85\end{align*}[/latex]
   2. [latex]\scriptsize W\hat{Z}X={{117.7}^\circ}[/latex] (given)
      [latex]\scriptsize W\hat{X}Z={{180}^\circ}-{{117.7}^\circ}-{{30}^\circ}={{32.3}^\circ}[/latex] (angles in a triangle are supplementary)
      [latex]\scriptsize WX\parallel YZ[/latex] (given)
      [latex]\scriptsize W\hat{X}Z=X\hat{Z}Y={{32.3}^\circ}[/latex] (alternate angles are equal, [latex]\scriptsize WX\parallel YZ[/latex])
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin Y}}{{XZ}} & =\displaystyle \frac{{\sin X\hat{Z}Y}}{{XY}}\\\therefore \displaystyle \frac{{\sin Y}}{{4.85}} & =\displaystyle \frac{{\sin {{{32.3}}^\circ}}}{{2.6}}\\\therefore \sin Y & =\displaystyle \frac{{4.85\times \sin {{{32.3}}^\circ}}}{{2.6}}\\\therefore \hat{Y} & ={{85.40}^\circ}\end{align*}[/latex]
   3. [latex]\scriptsize \text{area }WXYZ=\text{area }\Delta WXZ+\text{area }\Delta XYZ[/latex]
      [latex]\scriptsize \begin{align*}\text{area }\Delta WXZ&=\displaystyle \frac{1}{2}\times WZ\times WX\times \sin W\\&=\displaystyle \frac{1}{2}\times 5.2\times 8.6\times \sin {{30}^\circ}\\&=11.18\ {{\text{u}}^{2}}\end{align*}[/latex]
      .
      In [latex]\scriptsize \Delta XYZ[/latex]:
      [latex]\scriptsize \begin{align*}Z\widehat{X}Y&={{180}^\circ}-\hat{Y}-X\hat{Z}Y\\&={{180}^\circ}-{{85.40}^\circ}-{{32.3}^\circ}\\&={{62.3}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}\text{area }\Delta XYZ&=\displaystyle \frac{1}{2}\times XZ\times XY\times \sin Z\hat{X}Y\\&=\displaystyle \frac{1}{2}\times 4.85\times 2.6\times \sin {{62.3}^\circ}\\&=5.58\ {{\text{u}}^{2}}\end{align*}[/latex]
      Therefore [latex]\scriptsize \text{area }WXYZ=11.18+5.58=16.76\ {{\text{u}}^{2}}[/latex]

Back to Unit 7: Assessment