Unit 2 outcomes

By the end of this unit you will be able to:

• Find the equation of a quadratic function when given the x-intercepts and another point on the graph.
• Find the equation of a quadratic function when given the turning point and another point on the graph.

What you should know

Before you start this unit, make sure you can:

• Solve quadratic equations by:
  • Factorisation
  • Completing the square
  • Using the quadratic formula. Review unit 1 of subject outcome 2.3 for level 2 and unit 1, unit 2 and unit 3 of subject outcome 2.3 for level 3 for help with solving quadratic functions.
• Determine the x- and y-intercepts of a quadratic function.
• Plot quadratic functions of the form [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] and [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex]. Review unit 1 of subject outcome 2.1 for level 3.
• Determine the turning point of a quadratic functions of the form [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] and [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex]. Review unit 1 of subject outcome 2.1 for level 3.

Introduction

In the previous unit we learnt how to plot quadratic functions of the form [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] and [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex]. Remember that [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex] is the general form of the quadratic function and [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] is the turning point (TP) form of the quadratic where the turning point of the parabola is given by [latex]\scriptsize (-p,q)[/latex].

In this unit, we are going to learn how to find the equations of quadratic functions from their graphs. There are two basic situations that we will come across:

• Where we are given the x-intercepts and one other point.
• Where we are given the turning point and one other point.

Given the x-intercepts and a point

When we are given the x-intercepts and one other point, we use a factorised form of the general form of the quadratic function [latex]\scriptsize y=a(x-{{x}_{1}})(x-{{x}_{2}})[/latex]. We know that to find the x-intercepts we have to factorise the quadratic expression. Therefore, to find the expression from the x-intercepts we start with the factorised form and work backwards.

Work through Example 2.1 to see how this is done.

Example 2.1

Find the equation of the parabola of the function [latex]\scriptsize f(x)[/latex] from the graph.

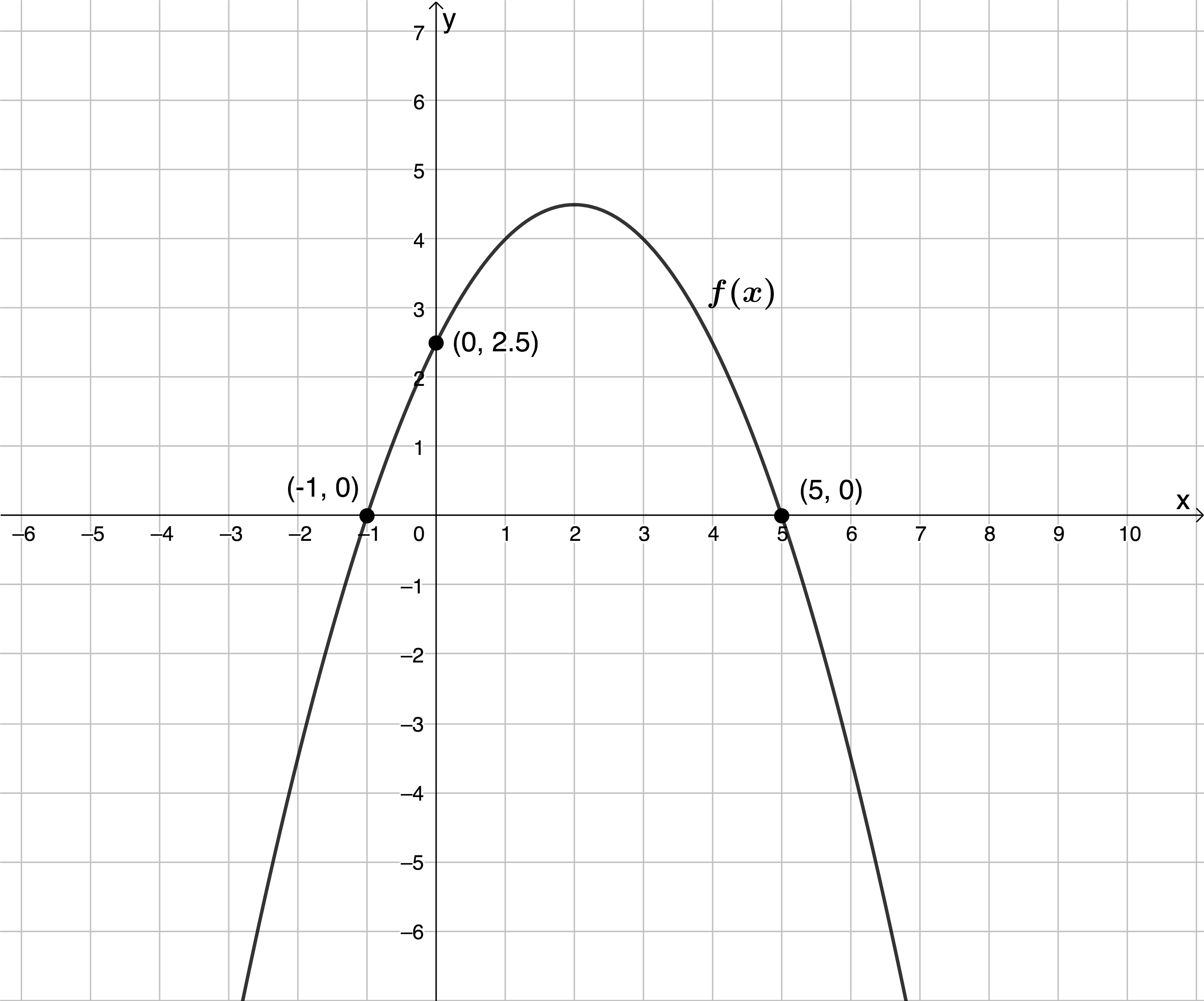
Solution

From the graph we can see that we have been given the x-intercepts and the y-intercept. We know that when we are plotting a quadratic function, we find the x-intercepts by solving the quadratic equation [latex]\scriptsize a{{x}^{2}}+bx+c=0[/latex]. When we factorise the left-hand side we get [latex]\scriptsize a(x-{{x}_{1}})(x-{{x}_{2}})=0[/latex]. We then use the zero product property to find the x-intercepts as [latex]\scriptsize {{x}_{1}}[/latex] and [latex]\scriptsize {{x}_{2}}[/latex].

If we are given the x-intercepts and we need to find the original equation, we have to reverse the process. We start with [latex]\scriptsize y=a(x-{{x}_{1}})(x-{{x}_{2}})[/latex] and substitute the given x-intercepts into the equation.

[latex]\scriptsize \begin{align*} y &=a\left( {x-(-1)} \right)\left( {x-5} \right)\text{Watch out for the negative sign in the first intercept}\\ \therefore y &=a(x+1)(x-5)\\ \therefore y &=a({{x}^{2}}-4x-5) \end{align*}[/latex]

But we still have an unknown of [latex]\scriptsize a[/latex] in our expression. Therefore, we need one other point to substitute in for [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] in order to solve for [latex]\scriptsize a[/latex]. In this example, that point is the y-intercept, but it could be any given point on the graph.

Substitute [latex]\scriptsize (0,2.5)[/latex] into [latex]\scriptsize y=a({{x}^{2}}-4x-5)[/latex].

[latex]\scriptsize \displaystyle \begin{align*}2.5 & =a\left( {{{0}^{2}}-4(0)-5} \right)\\\therefore 2.5 & =-5a\\\therefore a & =\displaystyle \frac{{2.5}}{{-5}}=-\displaystyle \frac{1}{2}\end{align*}[/latex]

For a quick check, we can see from the graph that [latex]\scriptsize a \lt 0[/latex].

Our final expression for this quadratic function in standard form is:
[latex]\scriptsize \begin{align*}y & =-\displaystyle \frac{1}{2}({{x}^{2}}-4x-5)\\\therefore y & =-\displaystyle \frac{1}{2}{{x}^{2}}+2x+\displaystyle \frac{5}{2}\end{align*}[/latex]

Sometimes you may be asked to give the function in the turning point form in which case you will need to complete the square.

Example 2.2

Find the equation of the parabola with an x-intercept of [latex]\scriptsize (-7,0)[/latex] an axis of symmetry (A/S) [latex]\scriptsize x=-\displaystyle \frac{{11}}{2}[/latex] and passing through the point [latex]\scriptsize (-2,30)[/latex].

Solution

In this case, it does not seem like we have enough information because we only have a single x-intercept. However, we are also given the A/S and we know that the x-intercepts are the same distance from the A/S, by definition. The A/S is the line the cuts a parabola into two mirror image halves.

The A/S is the line [latex]\scriptsize x=-\displaystyle \frac{{11}}{2}=-5.5[/latex] and one of the x-intercepts is [latex]\scriptsize (-7,0)[/latex]. This intercept is one and a half units to the left of the A/S. Therefore, the other x-intercept must be one and a half units to the right of the A/S. In other words, it is the point [latex]\scriptsize (-4,0)[/latex]. Now we have two x-intercepts and we can proceed as before by substituting these intercepts into [latex]\scriptsize y=a(x-{{x}_{1}})(x-{{x}_{2}})[/latex].

[latex]\scriptsize \begin{align*}y & =a\left( {x-(-7)} \right)\left( {x-(-4)} \right)\quad \text{Watch out for the negative signs}\\\therefore y & =a(x+7)(x+4)\\\therefore y & =a({{x}^{2}}+11x+28)\end{align*}[/latex]

Now substitute [latex]\scriptsize (-2,30)[/latex] into [latex]\scriptsize y=a({{x}^{2}}+11x+28)[/latex].
[latex]\scriptsize \displaystyle \begin{align*}30 & =a\left( {{{{(-2)}}^{2}}+11(-2)+28} \right)\\\therefore 30 & =a(4-22+28)\\\therefore 30 & =10a\\\therefore a & =\displaystyle \frac{{30}}{{10}}=3\end{align*}[/latex]

Our final expression for this quadratic function in standard form is:
[latex]\scriptsize \begin{align*}y & =3({{x}^{2}}+11x+28)\\\therefore y & =3{{x}^{2}}+33x+84\end{align*}[/latex]

Take note!

In cases where the parabola just touches the x-axis and there is only a single x-intercept, use the same value for both [latex]\scriptsize {{x}_{1}}[/latex] and [latex]\scriptsize {{x}_{2}}[/latex] in [latex]\scriptsize y=a(x-{{x}_{1}})(x-{{x}_{2}})[/latex].

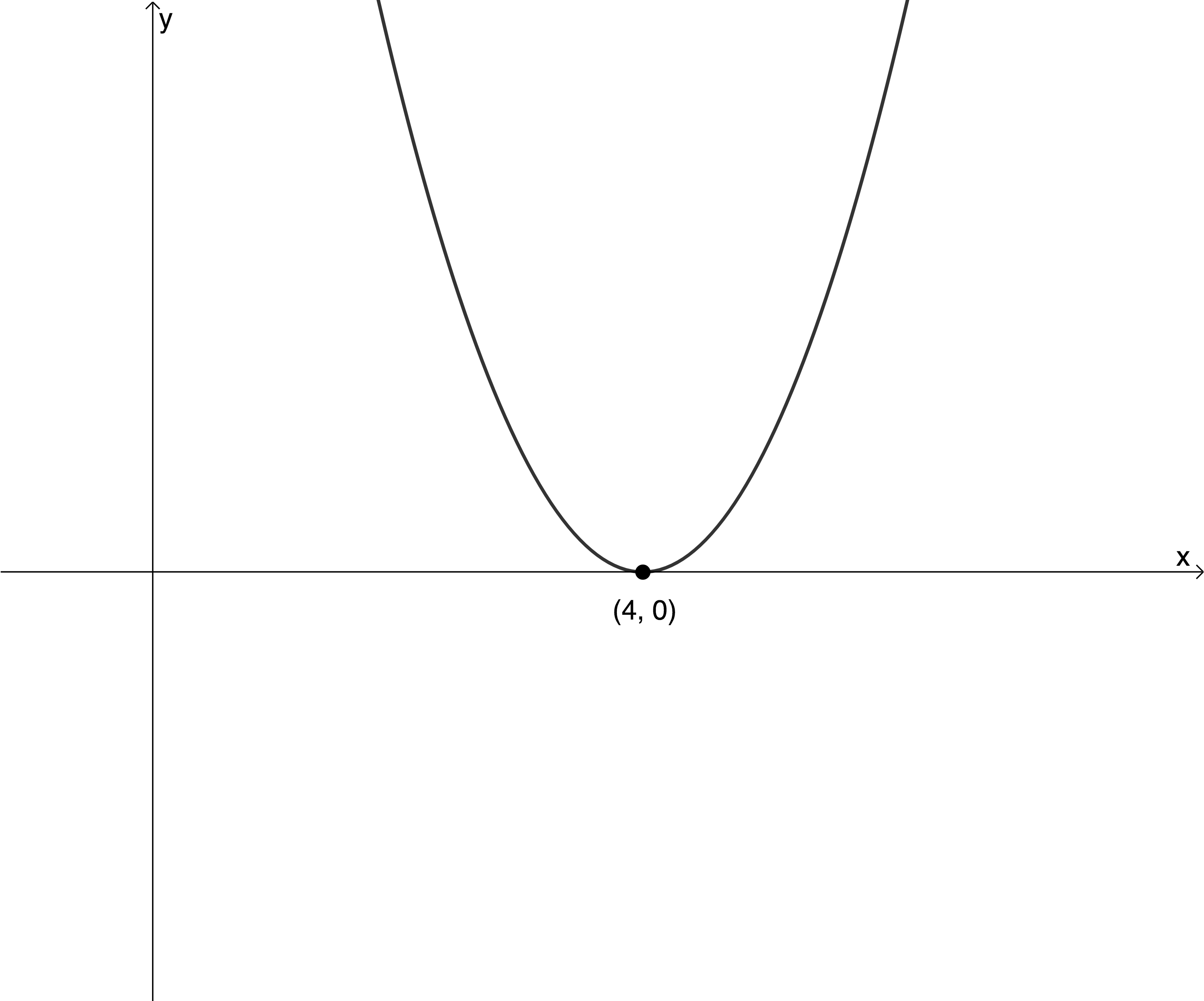
In the parabola above, both x-intercepts are the same point [latex]\scriptsize (4,0)[/latex].

Exercise 2.1

1. Find the equation of [latex]\scriptsize g(x)[/latex] from the graph.
   
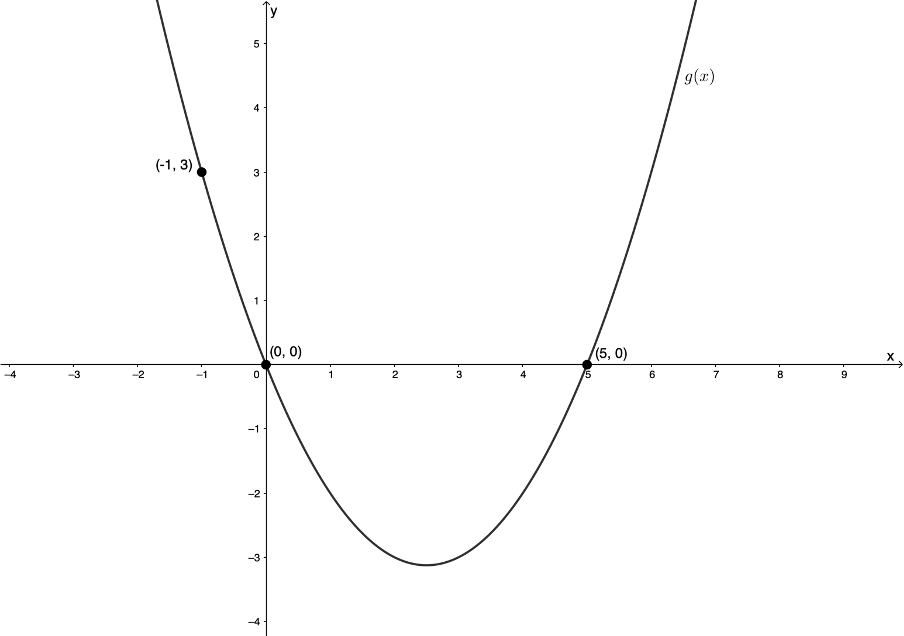
2. Find the equation of [latex]\scriptsize q(x)[/latex] from the graph.
   

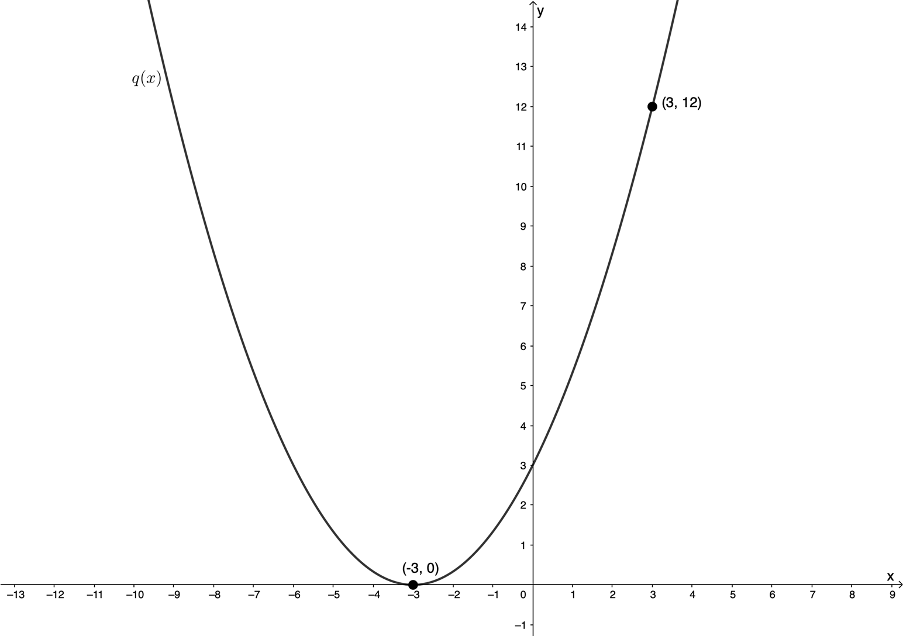
The full solutions are at the end of the unit.

Given the turning point and a point

When we are given the TP of a parabola, and we need to find the function, we start by substituting these values into the TP form of the quadratic equation, [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex]. Remember the TP is the point [latex]\scriptsize (-p,q)[/latex].

Work through Example 2.3 to see how.

Example 2.3

Find the equation of the parabola from the graph.

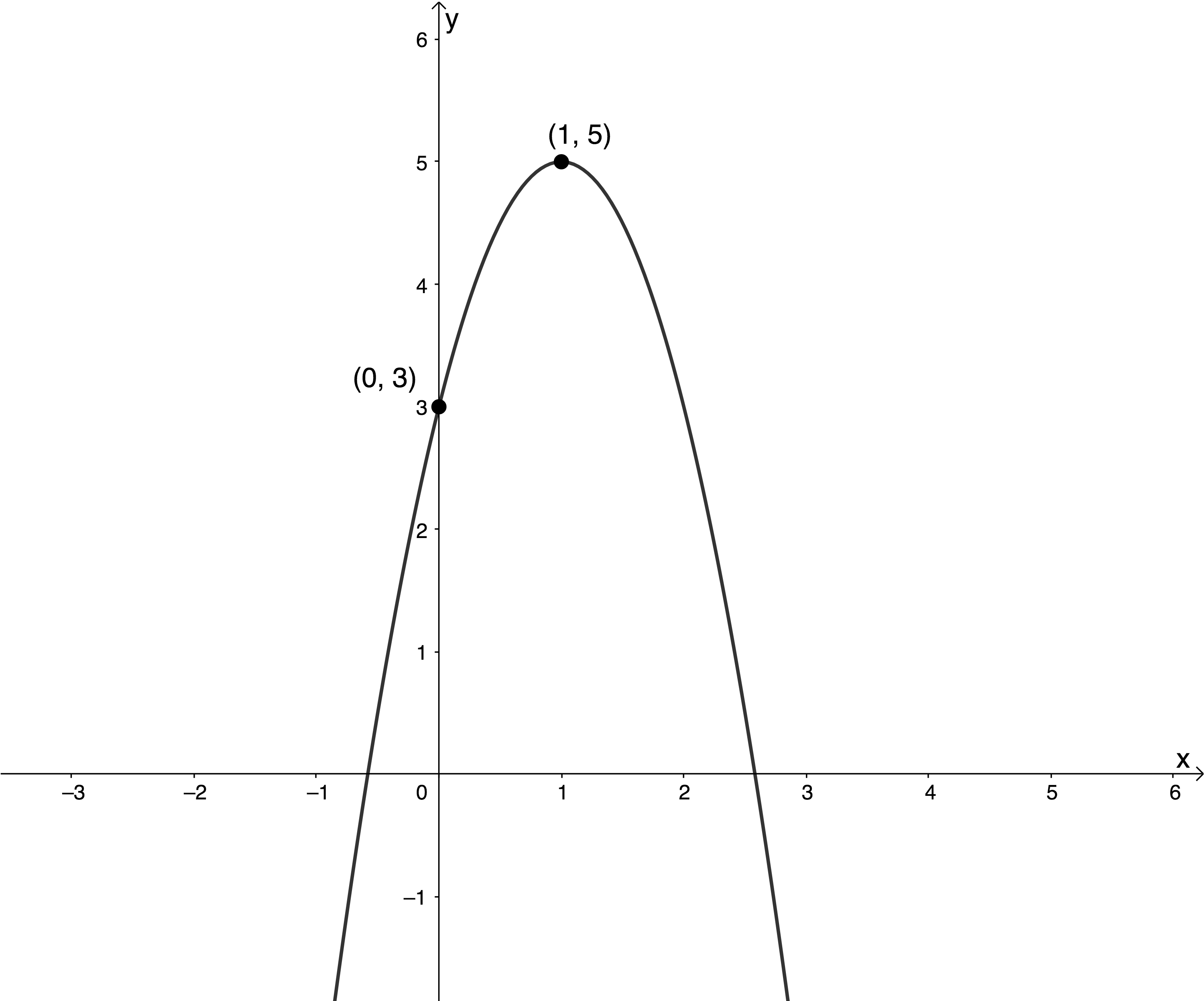
Solution

In this example, we have been given the turning point (TP) and another point on the graph. It just so happens that this other point is the y-intercept.

We know that in the turning point form of the quadratic function [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex], the TP is the point [latex]\scriptsize (-p,q)[/latex]. We know what the TP is, therefore, we know what the values of [latex]\scriptsize p[/latex] and [latex]\scriptsize q[/latex] are and can substitute these into the TP form.

[latex]\scriptsize \begin{align*}y=a{{(x-1)}^{2}}+5\\\therefore y=a({{x}^{2}}-2x+1)+5\end{align*}[/latex]

But we still have an unknown of [latex]\scriptsize a[/latex] in our equation. Therefore, we need one other point to substitute for [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] in order to solve for [latex]\scriptsize a[/latex]. In this example, that point is the y-intercept, but it could be any point on the graph.

Substitute [latex]\scriptsize (0,3)[/latex] into [latex]\scriptsize y=a({{x}^{2}}-2x+1)+5[/latex].
[latex]\scriptsize \displaystyle \begin{align*}3=a\left( {{{0}^{2}}-2(0)+1} \right)+5\\\therefore 3 & =a+5\\\therefore a & =-2\end{align*}[/latex]

Our final expression for this quadratic function in TP form is [latex]\scriptsize y=-2{{(x-1)}^{2}}+5[/latex].

Sometimes you may be asked to give the quadratic function in its standard form in which case you just need to expand and simplify to get [latex]\scriptsize y=-2{{x}^{2}}+4x+3[/latex].

Example 2.4

In the diagram below, [latex]\scriptsize s(x)[/latex] is a quadratic function with x-intercepts of [latex]\scriptsize -3[/latex] and [latex]\scriptsize 4[/latex]. [latex]\scriptsize \text{G}[/latex] is the y-intercept of [latex]\scriptsize s(x)[/latex]. [latex]\scriptsize t(x)[/latex] is a linear function with an x-intercept of [latex]\scriptsize -6[/latex]. [latex]\scriptsize t(x)[/latex] intersects [latex]\scriptsize s(x)[/latex] at [latex]\scriptsize (3,-3)[/latex]. [latex]\scriptsize \text{H}[/latex] is the y-intercept of [latex]\scriptsize t(x)[/latex].

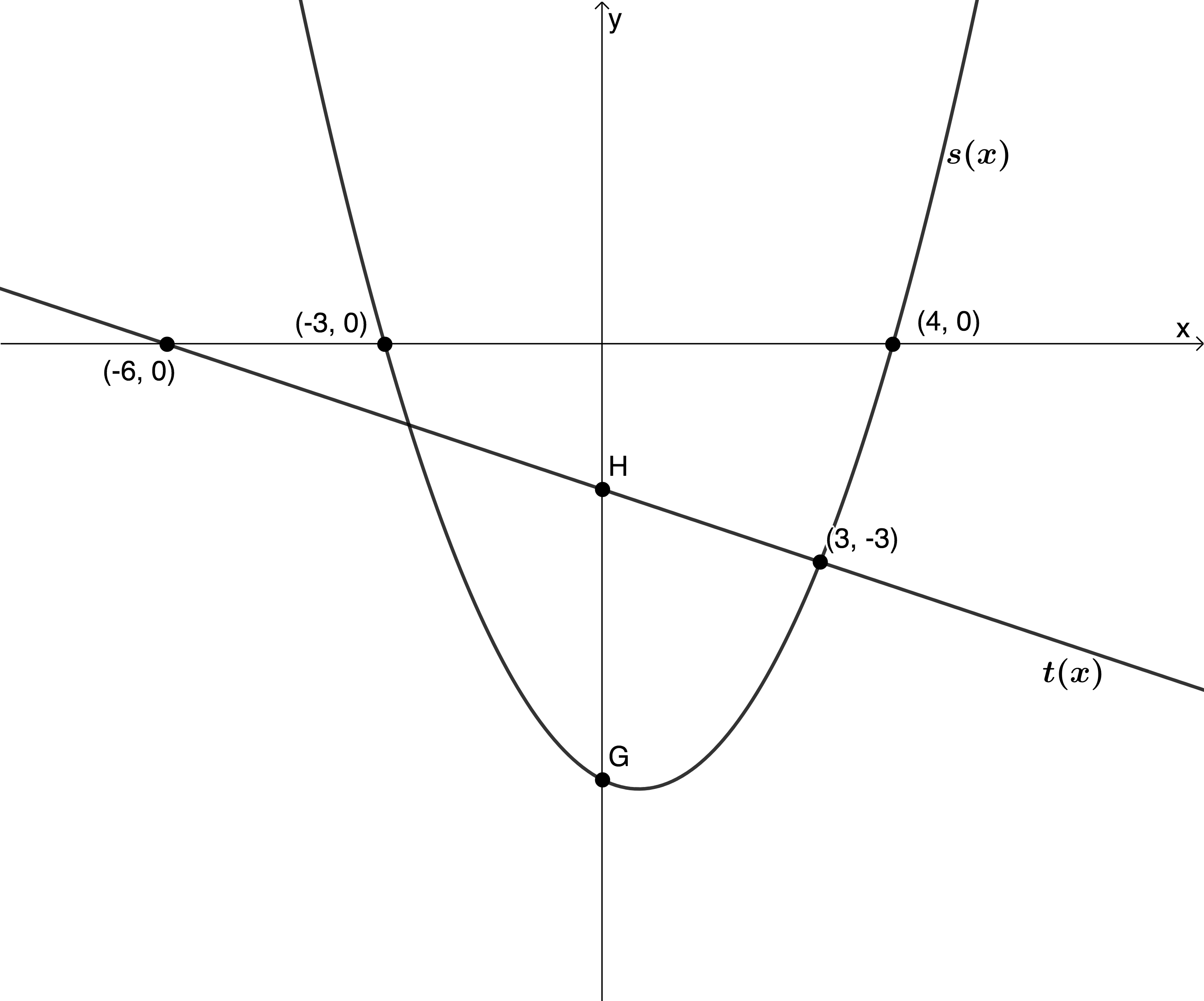
1. Determine the equation of [latex]\scriptsize s(x)[/latex].
2. Determine the equation of [latex]\scriptsize t(x)[/latex].
3. Find the distance [latex]\scriptsize \text{GH}[/latex].

Solutions

1. [latex]\scriptsize s(x)=a(x-{{x}_{1}})(x-{{x}_{2}})[/latex] where [latex]\scriptsize {{x}_{1}}=-3[/latex] and [latex]\scriptsize {{x}_{2}}=4[/latex].
   [latex]\scriptsize \begin{align*}s(x)&=a(x+3)(x-4)\\\therefore s(x)&=a({{x}^{2}}-x-12)\end{align*}[/latex]The point [latex]\scriptsize (3,-3)[/latex] lies on [latex]\scriptsize s(x)[/latex].

   [latex]\scriptsize \begin{align*}-3 & =a\left( {{{{(3)}}^{2}}-(3)-12} \right)\\\therefore -3 & =-6a\\\therefore a & =\displaystyle \frac{1}{2}\end{align*}[/latex]

   [latex]\scriptsize \begin{align*}s(x) & =\displaystyle \frac{1}{2}({{x}^{2}}-x-12)\\ & =\displaystyle \frac{1}{2}{{x}^{2}}-\displaystyle \frac{1}{2}x-6\end{align*}[/latex]

2. We know the equation of a straight line is given by [latex]\scriptsize y=mx+c[/latex]. Therefore, [latex]\scriptsize t(x)=mx+c[/latex].
   We have two points on the straight line so we can calculate the gradient.[latex]\scriptsize {{m}_{{t(x)}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{0-(-3)}}{{-6-3}}=\displaystyle \frac{3}{{-9}}=-\displaystyle \frac{1}{3}[/latex]

   But [latex]\scriptsize t(x)=-\displaystyle \frac{1}{3}x+c[/latex] passes through the point [latex]\scriptsize (3,-3)[/latex] so we can substitute these values for [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] and solve for [latex]\scriptsize c[/latex].

   [latex]\scriptsize \begin{align*}-3 & =-\displaystyle \frac{1}{3}(3)+c\\\therefore -3 & =-1+c\\\therefore c & =-2\end{align*}[/latex]

   [latex]\scriptsize t(x)=-\displaystyle \frac{1}{3}x-2[/latex]

3. To find the vertical distance between two functions we say the top graph minus the bottom graph. So, it is the top graph’s function value minus the bottom graph’s function value.[latex]\scriptsize \text{H}[/latex] is the y-intercept of [latex]\scriptsize t(x)[/latex]. Find [latex]\scriptsize t(0)[/latex].

   [latex]\scriptsize t(0)=-\displaystyle \frac{1}{3}(0)-2=-2[/latex]. Remember in [latex]\scriptsize y=mx+c[/latex], [latex]\scriptsize c[/latex] is the y-intercept.

   [latex]\scriptsize \text{G}[/latex] is the y-intercept of [latex]\scriptsize s(x)[/latex]. Find [latex]\scriptsize s(0)[/latex].

   [latex]\scriptsize s(0) =\displaystyle \frac{1}{2}{{(0)}^{2}}-\displaystyle \frac{1}{2}(0)-6=-6[/latex]. Remember that in [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex], [latex]\scriptsize c[/latex] is the y-intercept.

   Therefore

   [latex]\scriptsize \begin{align*}\text{GH}&=-2-(-6)\\&=4\end{align*}[/latex].

Exercise 2.2

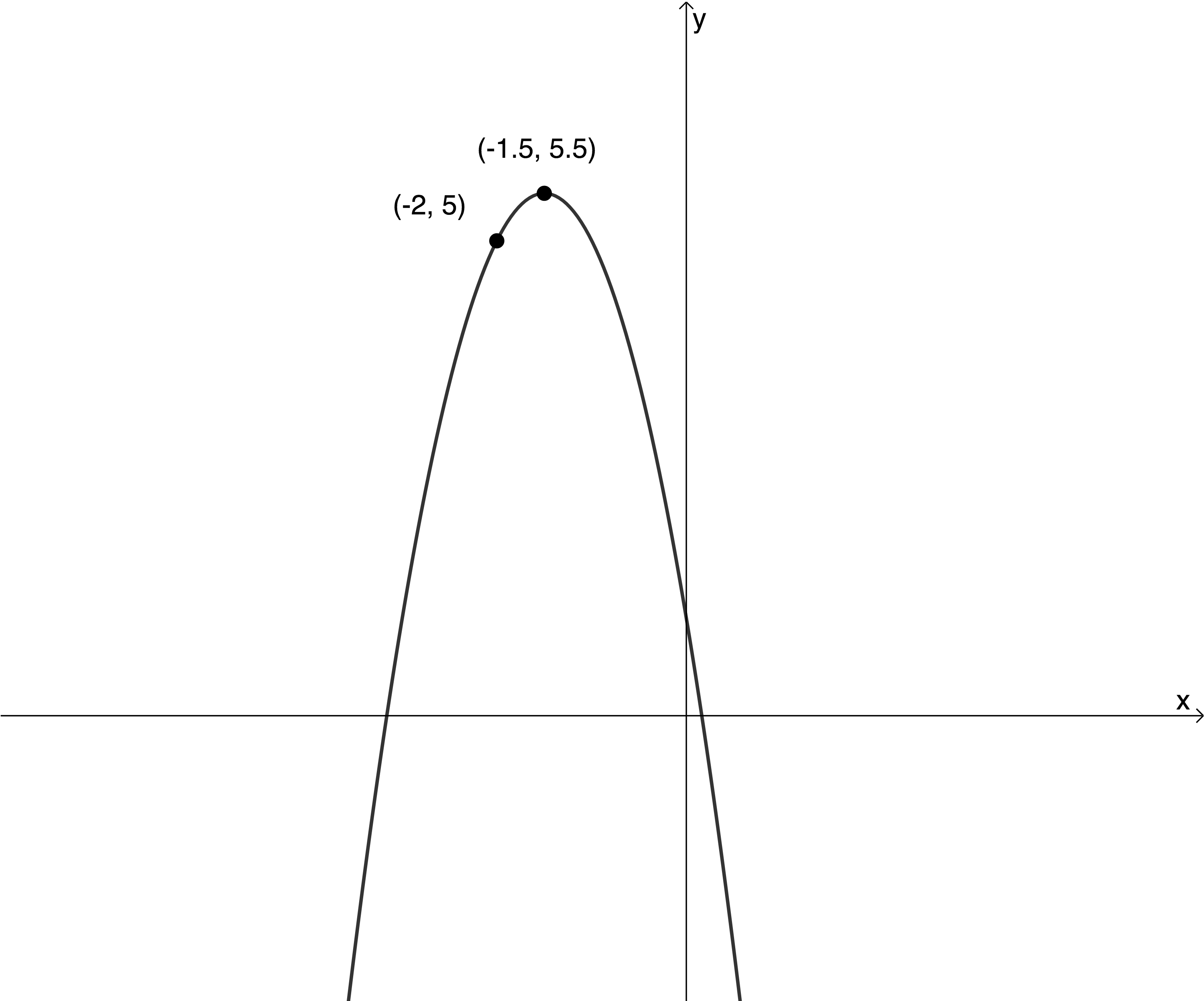
1. Find the equation of the parabola from the graph in TP form.
   
2. The quadratic function [latex]\scriptsize k(x)[/latex] has a turning point of [latex]\scriptsize (2,-5)[/latex] and a y-intercept of [latex]\scriptsize (0,-4)[/latex]. What is the equation of the function in turning point form?

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to find the equation of a quadratic function when given the x-intercepts and one other point.
• How to find the equation of a quadratic function when given the turning point and one other point.

Unit 2: Assessment

Suggested time to complete: 40 minutes

1. The system of axes given below shows the graphs of [latex]\scriptsize f(x)[/latex] and [latex]\scriptsize g(x)[/latex]. The graph given as [latex]\scriptsize f(x)[/latex] is a parabola which cuts the x-axis at [latex]\scriptsize -1[/latex] and [latex]\scriptsize 3[/latex] and has a y-intercept of [latex]\scriptsize 6[/latex]. The graph given as [latex]\scriptsize g(x)[/latex] is a straight line that passes through the points [latex]\scriptsize (0,-2)[/latex] and [latex]\scriptsize (3,0)[/latex]. The two graphs intersect at the points [latex]\scriptsize (3,0)[/latex] and [latex]\scriptsize (p,q)[/latex].
   
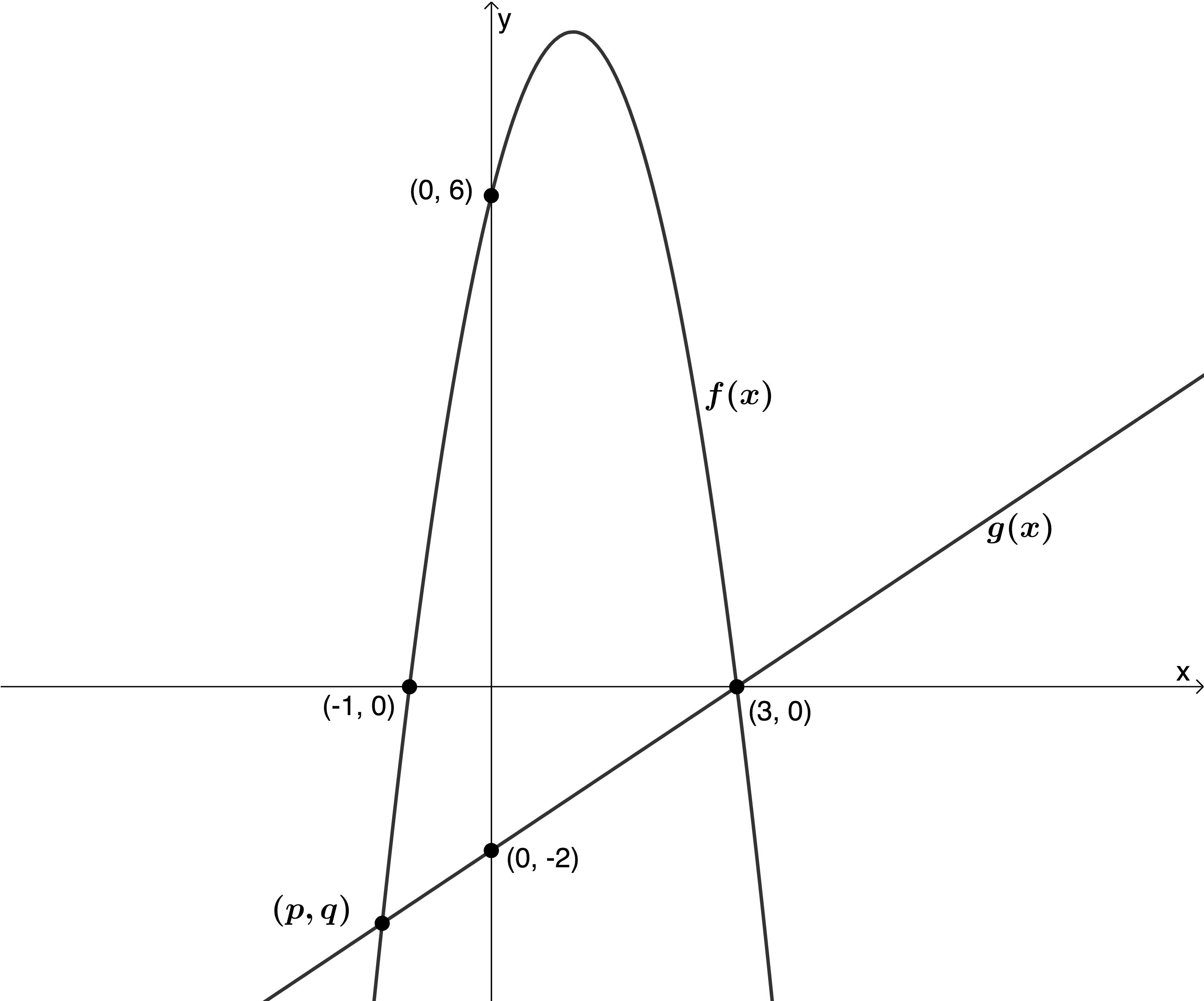
   1. Determine the equation of [latex]\scriptsize f(x)[/latex].
   2. Determine the equation of [latex]\scriptsize g(x)[/latex].
   3. Find the values of [latex]\scriptsize p[/latex] and [latex]\scriptsize q[/latex].
   4. Use the graph to determine the values of [latex]\scriptsize x[/latex] for which [latex]\scriptsize f(x).g(x)\ge 0[/latex].
2. What are the x-intercepts of the quadratic function that has a turning point of [latex]\scriptsize (2,-2)[/latex] and passes through the point [latex]\scriptsize \left( {3,\displaystyle \frac{3}{2}} \right)[/latex]?
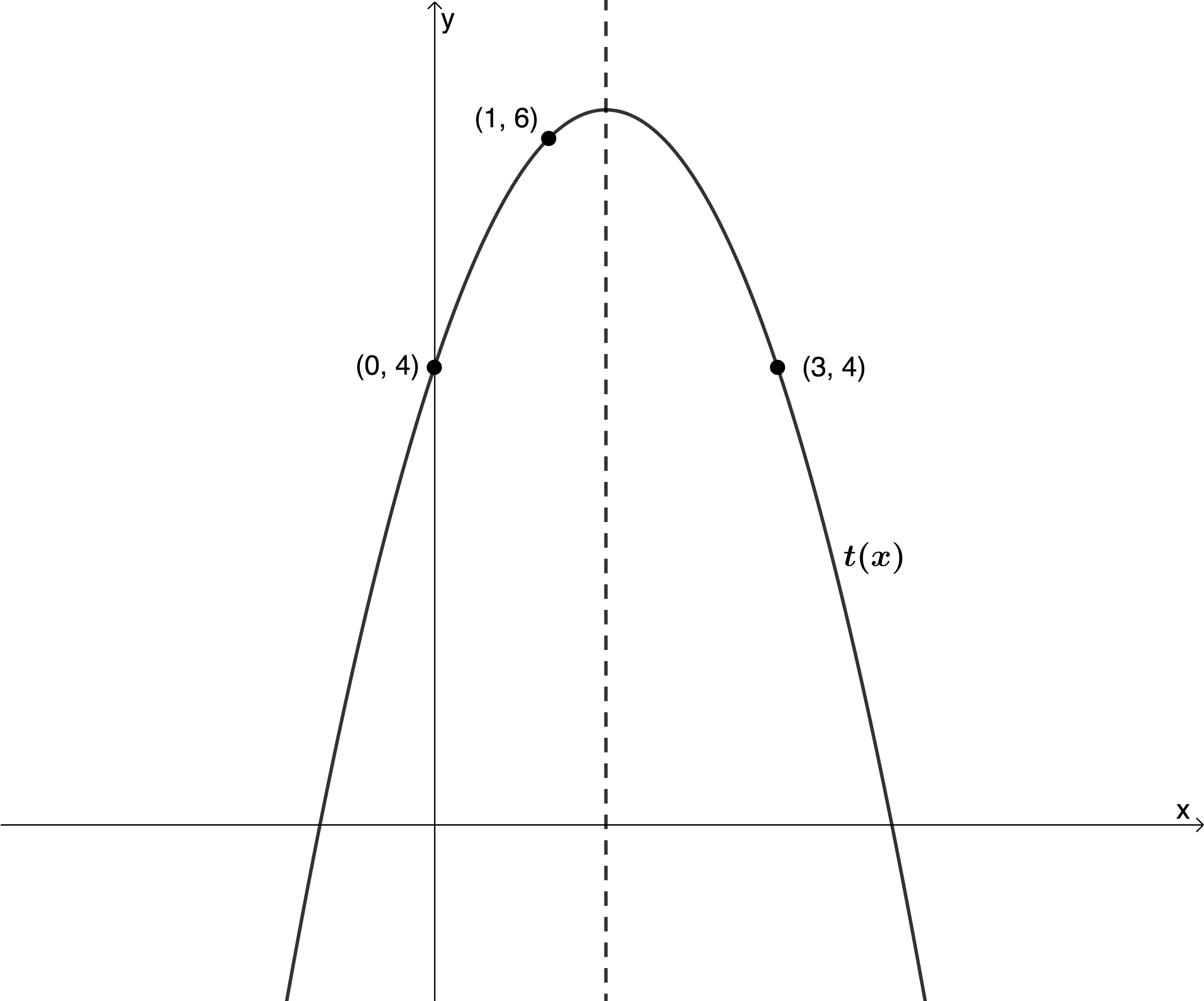
3. Determine the equation of [latex]\scriptsize t(x)[/latex] from the graph. HINT: Remember that the axis of symmetry divides the parabola into two mirror image halves. The standard form of the quadratic function is [latex]\scriptsize y=a{{x}^{2}}+bx+c[/latex]. The A/S is given by [latex]\scriptsize x=-\displaystyle \frac{b}{{2a}}[/latex].
   

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. [latex]\scriptsize g(x)=a(x-{{x}_{1}})(x-{{x}_{2}})[/latex] where [latex]\scriptsize {{x}_{1}}=0[/latex] and [latex]\scriptsize {{x}_{2}}=5[/latex].
   [latex]\scriptsize \begin{align*}g(x) & =a(x-0)(x-5)\\\therefore g(x) & =a(x)(x-5)\\\therefore g(x) & =a({{x}^{2}}-5x)\end{align*}[/latex]
   The point [latex]\scriptsize (-1,3)[/latex] lies on [latex]\scriptsize g(x)[/latex].
   [latex]\scriptsize \begin{align*}3 & =a\left( {{{{(-1)}}^{2}}-5(-1)} \right)\\\therefore 3 & =6a\\\therefore a & =\displaystyle \frac{1}{2}\end{align*}[/latex]
   The quadratic function has the equation:
   [latex]\scriptsize \begin{align*}g(x) & =\displaystyle \frac{1}{2}({{x}^{2}}-5x)\\\therefore g(x) & =\displaystyle \frac{1}{2}{{x}^{2}}-\displaystyle \frac{5}{2}x\end{align*}[/latex]
2. [latex]\scriptsize q(x)=a(x-{{x}_{1}})(x-{{x}_{2}})[/latex] where [latex]\scriptsize {{x}_{1}}=-3[/latex] and [latex]\scriptsize {{x}_{2}}=-3[/latex].
   [latex]\scriptsize \begin{align*}q(x) & =a(x+3)(x+3)\\\therefore q(x) & =a({{x}^{2}}+6x+9)\end{align*}[/latex]
   The point [latex]\scriptsize (3,12)[/latex] lies on [latex]\scriptsize q(x)[/latex].
   [latex]\scriptsize \begin{align*}12&=a\left( {{{{(3)}}^{2}}+6(3)+9} \right)\\\therefore 12 & =36a\\\therefore a & =\displaystyle \frac{1}{3}\end{align*}[/latex]
   The quadratic function has the equation:
   [latex]\scriptsize \begin{align*}q(x) & =\displaystyle \frac{1}{3}({{x}^{2}}+6x+9)\\\therefore q(x) & =\displaystyle \frac{1}{3}{{x}^{2}}+2x+3\end{align*}[/latex]

Back to Exercise 2.1

Exercise 2.2

1. [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] where the TP is [latex]\scriptsize (-1.5,5.5)[/latex] or [latex]\scriptsize \left( {-\displaystyle \frac{3}{2},\displaystyle \frac{{11}}{2}} \right)[/latex].
   [latex]\scriptsize \begin{align*}y=a{{\left( {x+\displaystyle \frac{3}{2}} \right)}^{2}}+\displaystyle \frac{{11}}{2}\\\therefore y=a\left( {{{x}^{2}}+3x+\displaystyle \frac{9}{4}} \right)+\displaystyle \frac{{11}}{2}\end{align*}[/latex]
   The point [latex]\scriptsize (-2,5)[/latex] lies on the graph.
   [latex]\scriptsize \begin{align*}5 & =a\left( {{{{(-2)}}^{2}}+3(-2)+\displaystyle \frac{9}{4}} \right)+\displaystyle \frac{{11}}{2}\\\therefore 5 & =a\left( {4-6+\displaystyle \frac{9}{4}} \right)+\displaystyle \frac{{11}}{2}\\\therefore 5 & =\displaystyle \frac{1}{4}a+\displaystyle \frac{{11}}{2}\\\therefore 20 & =a+22\\\therefore a & =-2\end{align*}[/latex]
   The quadratic function has the equation:
   [latex]\scriptsize y=-2{{\left( {x+\displaystyle \frac{3}{2}} \right)}^{2}}+\displaystyle \frac{{11}}{2}[/latex] in TP form.
2. [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] where the TP is [latex]\scriptsize (2,-5)[/latex].
   [latex]\scriptsize \begin{align*}y & =a{{\left( {x-2} \right)}^{2}}-5\\\therefore y & =a\left( {{{x}^{2}}-4x+4} \right)-5\end{align*}[/latex]
   The point [latex]\scriptsize (0,-4)[/latex] lies on the graph.
   [latex]\scriptsize \begin{align*}-4 & =a\left( {{{{(0)}}^{2}}-4(0)+4} \right)-5\\\therefore -4 & =4a-5\\\therefore 4a & =1\\\therefore a&=\displaystyle \frac{1}{4}\end{align*}[/latex]
   The quadratic function has the equation:
   [latex]\scriptsize y =\displaystyle \frac{1}{4}{{\left( {x-2} \right)}^{2}}-5[/latex]

Back to Exercise 2.2

Unit 2: Assessment

1. .
   1. [latex]\scriptsize f(x)=a(x-{{x}_{1}})(x-{{x}_{2}})[/latex] where [latex]\scriptsize {{x}_{1}}=-1[/latex] and [latex]\scriptsize {{x}_{2}}=3[/latex].
      [latex]\scriptsize \begin{align*}f(x) & =a(x+1)(x-3)\\\therefore f(x) & =a({{x}^{2}}-2x-3)\end{align*}[/latex]
      The point [latex]\scriptsize (0,6)[/latex] lies on the graph.
      [latex]\scriptsize \begin{align*}6 & =a\left( {{{{(0)}}^{2}}-2(0)-3} \right)\\\therefore 6 & =-3a\\\therefore a & =-2\end{align*}[/latex]
      [latex]\scriptsize f(x)=-2({{x}^{2}}-2x-3)=-2{{x}^{2}}+4x+6[/latex].
   2. [latex]\scriptsize g(x)=mx+c[/latex] where [latex]\scriptsize c=-2[/latex]. [latex]\scriptsize {{m}_{{g(x)}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{-2-0}}{{0-3}}=\displaystyle \frac{2}{3}[/latex]
      [latex]\scriptsize g(x)=\displaystyle \frac{2}{3}x-2[/latex].
   3. The point [latex]\scriptsize (p,q)[/latex] is where [latex]\scriptsize f(x)[/latex] and [latex]\scriptsize g(x)[/latex] intersect.
      [latex]\scriptsize \begin{align*}f(x) & =g(x)\\\therefore -2{{x}^{2}}+4x+6 & =\displaystyle \frac{2}{3}x-2\\\therefore -6{{x}^{2}}+12x+18 & =2x-6\\\therefore -6{{x}^{2}}+10x+24 & =0\\\therefore 3{{x}^{2}}-5x-12 & =0\\\therefore (3x+4)(x-3) & =0\\\therefore x=-\displaystyle \frac{4}{3}\text{ } & \text{or }x=3\end{align*}[/latex]
      [latex]\scriptsize p=-\displaystyle \frac{4}{3}[/latex]. Substitute into [latex]\scriptsize x=-\displaystyle \frac{4}{3}[/latex] into [latex]\scriptsize g(x)[/latex].
      [latex]\scriptsize \begin{align*}g\left( {-\displaystyle \frac{4}{3}} \right) & =\displaystyle \frac{2}{3}\left( {-\displaystyle \frac{4}{3}} \right)-2\\ & =-\displaystyle \frac{8}{9}-\displaystyle \frac{{18}}{9}\\ & =-\displaystyle \frac{{26}}{9}\end{align*}[/latex]
      [latex]\scriptsize q=-\displaystyle \frac{{26}}{9}[/latex]
   4. [latex]\scriptsize f(x).g(x)\ge 0[/latex] when [latex]\scriptsize f(x)\le 0[/latex] and [latex]\scriptsize g(x)\le 0[/latex] or [latex]\scriptsize f(x)\ge 0[/latex] and [latex]\scriptsize g(x)\ge 0[/latex]. Therefore [latex]\scriptsize f(x).g(x)\ge 0[/latex] for [latex]\scriptsize x\in (-\infty ,-1][/latex].
2. First, we need to find the equation of the quadratic function.
   [latex]\scriptsize y=a{{(x+p)}^{2}}+q[/latex] where the TP is [latex]\scriptsize (2,-2)[/latex].
   [latex]\scriptsize \begin{align*}y & =a{{\left( {x-2} \right)}^{2}}-2\\\therefore y & =a\left( {{{x}^{2}}-4x+4} \right)-2\end{align*}[/latex]
   The point [latex]\scriptsize \left( {3,-\displaystyle \frac{3}{2}} \right)[/latex] lies on the graph.
   [latex]\scriptsize \begin{align*}-\displaystyle \frac{3}{2} & =a\left( {{{{(3)}}^{2}}-4(3)+4} \right)-2\\\therefore -\displaystyle \frac{3}{2} & =a-2\\\therefore a & =\displaystyle \frac{1}{2}\end{align*}[/latex]
   The quadratic function has the equation:
   [latex]\scriptsize y =\displaystyle \frac{1}{2}{{\left( {x-2} \right)}^{2}}-2[/latex]
   To find the x-intercepts, we need to expand the quadratic function into standard form, set the function equal to zero and solve for [latex]\scriptsize x[/latex].
   [latex]\scriptsize \begin{align*}y & =\displaystyle \frac{1}{2}{{\left( {x-2} \right)}^{2}}-2\\\therefore y=\displaystyle \frac{1}{2}({{x}^{2}}-4x+4)-2\\\therefore y=\displaystyle \frac{1}{2}{{x}^{2}}-2x+2-2\\\therefore y=\displaystyle \frac{1}{2}{{x}^{2}}-2x\end{align*}[/latex]
   Let [latex]\scriptsize y=0[/latex]:
   [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{2}{{x}^{2}}-2x & =0\\\therefore {{x}^{2}}-4x & =0\\\therefore x(x-4) & =0\\\therefore x=0\text{ } & \text{or }x=4\end{align*}[/latex]
   The x-intercepts are [latex]\scriptsize 0[/latex] and [latex]\scriptsize 4[/latex].
3. We are given three points on the graph but none of them are x-intercepts or the TP. The point [latex]\scriptsize (0,4)[/latex] is the y-intercept. From two of the points, we can work out what the A/S is. The points [latex]\scriptsize (0,4)[/latex] and [latex]\scriptsize (3,4)[/latex] are reflected about the A/S and so the A/S is halfway between them. Halfway between [latex]\scriptsize 0[/latex] and [latex]\scriptsize 3[/latex] is [latex]\scriptsize \displaystyle \frac{3}{2}[/latex]. Therefore, the A/S is the line [latex]\scriptsize x=\displaystyle \frac{3}{2}[/latex].
   We know that the A/S is given by [latex]\scriptsize \displaystyle \frac{{-b}}{{2a}}[/latex]. Therefore:
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{-b}}{{2a}} & =\displaystyle \frac{3}{2}\\\therefore -2b & =6a\\\therefore b & =-3a\quad \text{Equation 1}\end{align*}[/latex]
   The graph passes through the point [latex]\scriptsize (1,6)[/latex] so [latex]\scriptsize 6=a{{(1)}^{2}}+b(1)+c[/latex]. But we know that the y-intercept is [latex]\scriptsize 4[/latex]. Therefore [latex]\scriptsize c=4[/latex].
   [latex]\scriptsize \begin{align*}6 & =a{{(1)}^{2}}+b(1)+4\\\therefore 6 & =a+b+4\\\therefore a & =-b+2\quad \text{Equation 2}\end{align*}[/latex]
   Substitute equation [latex]\scriptsize 1[/latex] into equation [latex]\scriptsize 2[/latex]:
   [latex]\scriptsize \begin{align*}a & =-(-3a)+2\\\therefore a=3a+2\\\therefore 2a & =-2\\\therefore a & =-1\end{align*}[/latex]
   Substitute [latex]\scriptsize a=-1[/latex] into equation [latex]\scriptsize 1[/latex]:
   [latex]\scriptsize \begin{align*}b & =-3\left( {-1} \right)\\\therefore b & =3\end{align*}[/latex]
   The equation of the quadratic function is [latex]\scriptsize t(x)=-{{x}^{2}}+3x+4[/latex].

Back to Unit 2: Assessment