Unit outcomes

By the end of this unit you will be able to:

• Use differentiation to find optimal solutions.

What you should know

Before you start this unit, make sure you can:

• Use the rules of differentiation to find the derivative. The rules of differentiation are covered in unit 3 of this subject outcome.

Introduction

One common application of calculus is to calculate the smallest or largest value of a function. Finding the maximum and minimum values of a function has many real-life applications because we can use this method to solve optimisation problems – problems that require some variable to be maximised or minimised.

Examples of optimisation problems include maximising profit, minimising the amount of material used in manufacturing or finding the maximum height a rocket can reach. In this unit, we use derivatives to find the maximum and minimum values of a function.

Activity 4.1: Functions and optimisation

Time required: 20 minutes

What you need:

• pen and paper

What to do:

The fuel used by a car is defined by [latex]\scriptsize f(v)=\displaystyle \frac{3}{{80}}{{v}^{2}}-6v+245[/latex], where [latex]\scriptsize v[/latex] is the travelling speed in km/h.

1. Plot speed on the x-axis and fuel consumption on the y-axis to draw the graph of [latex]\scriptsize f[/latex]. Use a scale of [latex]\scriptsize 1:10[/latex] on the axes. Notice that the function is a quadratic function.
2. At what speed is the least fuel consumed?
3. Find [latex]\scriptsize {f}'(v)[/latex].
4. Let [latex]\scriptsize {f}'(v)=0[/latex] and solve for [latex]\scriptsize v[/latex]. What have you found?
5. Comment on the answers you got in questions 2 and 5.

What did you find?

1. .
   
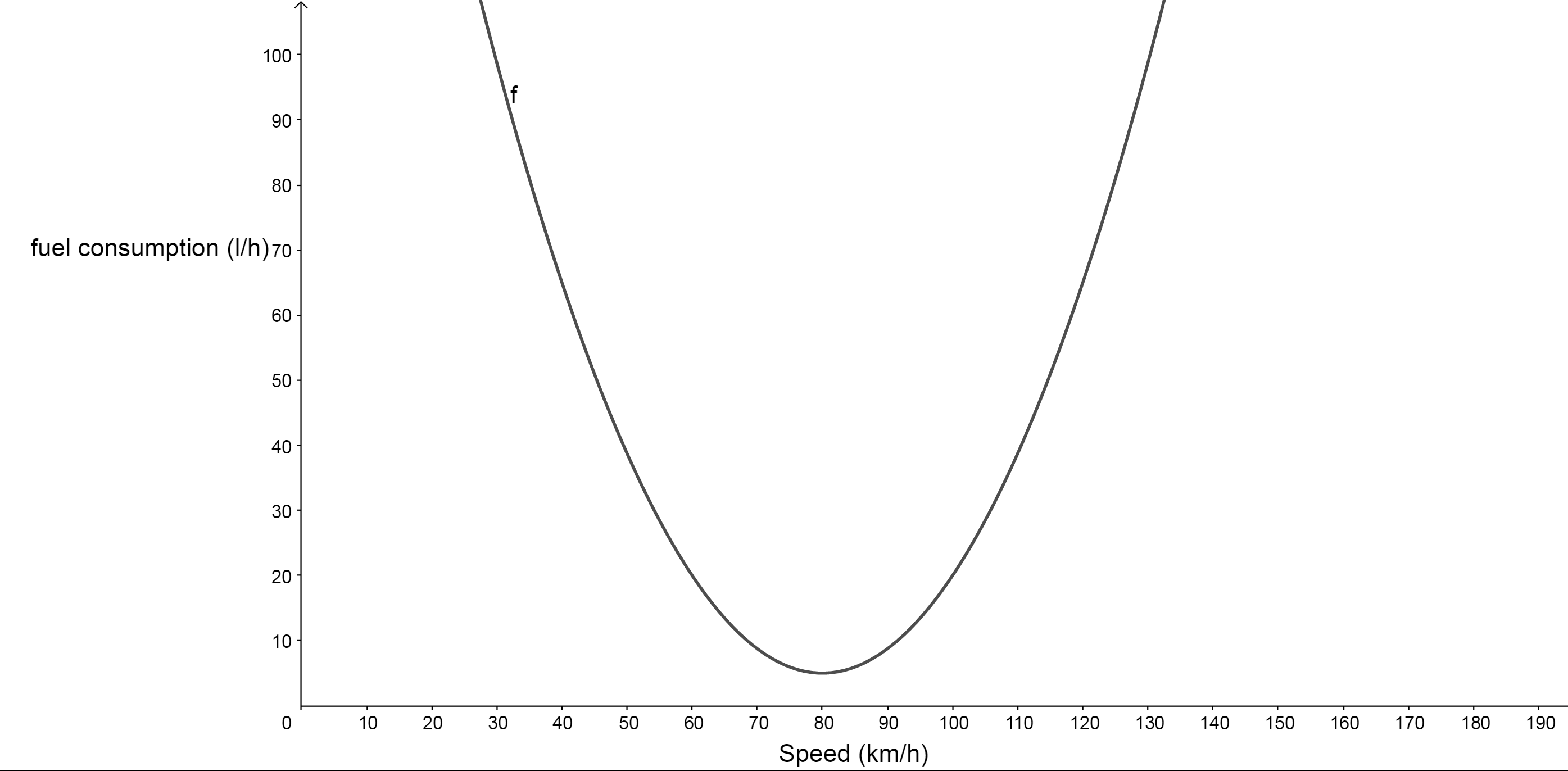
2. The least fuel usage will be found at the lowest part of the graph or the minimum value of the graph. The speed at the minimum would then give the most economical speed. Therefore, the least fuel is consumed at [latex]\scriptsize 80[/latex]km/h.
3. .
   [latex]\scriptsize \begin{align*}f(v)&=\displaystyle \frac{3}{{80}}{{v}^{2}}-6v+245\\{f}'(v)&=\displaystyle \frac{3}{{80}}(2){{v}^{{2-1}}}-6{{v}^{{1-1}}}+0\\&=\displaystyle \frac{3}{{40}}v-6\end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*}{f}'(v) & =0\\\displaystyle \frac{3}{{40}}v-6 & =0\\\therefore v & =\displaystyle \frac{{6\times 40}}{3}\\ & =80\end{align*}[/latex]
   We have found the speed that corresponds to the minimum fuel consumption.
5. We see that we can find the x-coordinate of the turning point of a function by differentiating (speed in this example) and letting the derivative equal zero. If we set [latex]\scriptsize {f}'(v)=0[/latex] we can calculate the speed that corresponds to the minimum turning point, which is also known as a stationary point.
   .
   This means that the most economical speed of [latex]\scriptsize 80[/latex] km/h can also be found by equating the derivative to zero.

Take note!

To find the optimum point using calculus:

Let [latex]\scriptsize {f}'(x)=0[/latex] and solve for [latex]\scriptsize x[/latex].

To check whether the optimum point is a local minimum or a local maximum without drawing the graph, we must find the second derivative. You will learn more about the second derivative in level 4.

• If [latex]\scriptsize {{f}'}'(x) \lt 0[/latex], then the point is a local maximum.
• If [latex]\scriptsize {{f}'}'(x) \gt 0[/latex], then the point is a local minimum.

Example 4.1

Jacky wants to put a fence around her vegetable garden. She decides to fence it off in the shape of a rectangle and only has [latex]\scriptsize 160\text{ m}[/latex] of fencing so she uses a rock wall as the one border of the garden. Calculate the width and length of the garden that corresponds to the largest possible area that Jacky can fence off.

Solution

Step 1: Read the question carefully, draw a diagram if necessary and decide what variables need to be used.

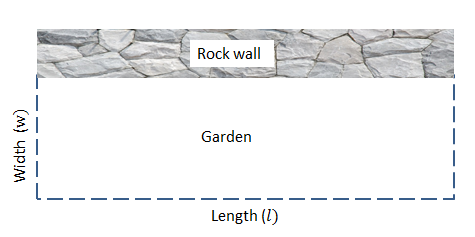
Let the width be [latex]\scriptsize w[/latex] and the length be [latex]\scriptsize l[/latex].

Step 2: Determine which quantity needs to be maximised or minimised. Write a formula for the quantity to be maximised or minimised in terms of the variables.

We are given information about the area and the modified perimeter of the garden. We know that the area of the garden is given by the formula:

[latex]\scriptsize \text{Area}=l\times w[/latex]

Write any other equations relating the independent variables in the formula found above. Use these equations to write the quantity to be maximised or minimised (area in this case) as a function of one variable.

The fencing is only required for three sides and the three sides must add up to [latex]\scriptsize \displaystyle 160\text{ m}[/latex]. So we can say the perimeter is:

[latex]\scriptsize w+w+l=160[/latex]

Rearrange the formula and make [latex]\scriptsize l[/latex] the subject of the formula.

[latex]\scriptsize l=160-2w[/latex]

Substitute the expression for [latex]\scriptsize l[/latex] into the formula for the area of the garden. Notice that this formula now contains only one unknown variable.

[latex]\scriptsize \begin{align*}\text{Area}&=w(160-2w)\\&=160w-2{{w}^{2}}\end{align*}[/latex]

Step 3: Differentiate with respect of the variable to find the maximum or minimum value.

We are interested in maximising the area of the garden, so we differentiate to get the following:

[latex]\scriptsize \displaystyle \frac{{dA}}{{dw}}={A}'(w)=160-4w[/latex]

Step 4: Calculate the stationary point (point on a graph where a minimum or maximum value is found).

To find the stationary point, we set [latex]\scriptsize {A}'=0[/latex] and solve to find the value(s) of [latex]\scriptsize w[/latex] that maximises the area.

[latex]\scriptsize \begin{align*}{A}'(w)&=160-4w\\0&=160-4w\\4w&=160\\w&=40\end{align*}[/latex]

Therefore, the width of the garden is [latex]\scriptsize 40\text{ m}[/latex].

Substitute to solve for the length.

[latex]\scriptsize \begin{align*}l&=160-2w\\&=160-2(40)\\&=80\end{align*}[/latex]

Therefore, the length of the garden is [latex]\scriptsize 80\text{ m}[/latex].

We can check that these dimensions give a maximum area by finding the second derivative.

For a maximum value [latex]\scriptsize {A}''(w) \lt 0[/latex]:

[latex]\scriptsize \begin{align*}{A}'(w) & =160-4w\\\therefore {A}''(w) & =-4\end{align*}[/latex]

[latex]\scriptsize \because {A}'' \lt 0[/latex] The maximum area of the garden is reached when [latex]\scriptsize w=40[/latex].

Therefore, a width of [latex]\scriptsize 40\text{ m}[/latex] and a length of [latex]\scriptsize 80\text{ m}[/latex] gives the maximum area of the garden.

Take note!

Here is a problem-solving strategy for maxima and minima questions:

1. Read the question carefully, draw a diagram if necessary and decide what variables need to be used.
2. Determine which quantity needs to be maximised or minimised. If necessary, write a formula for the quantity to be maximised or minimised in terms of the variables.
3. The quantity that needs to be minimised or maximised must be expressed in terms of only one variable. So write any other information relating to the variables in another equation and use this equation to substitute for one variable in terms of the other.
4. Find the derivative of your equation with only one variable.
5. Set the derivative equal to zero and solve to find the value that will minimise or maximise the problem.
6. Find the second derivative to confirm that the value you found is the minimum or maximum value.

The next example looks at maximising profit.

Example 4.2

A factory has [latex]\scriptsize x[/latex] employees and makes a profit of [latex]\scriptsize P[/latex] rand per week. The relationship between the profit and number of employees is given by [latex]\scriptsize P\left( x \right)=-2{{x}^{3}}+600x+1~000[/latex].

1. Calculate the number of employees needed for the factory to make a maximum profit.
2. Confirm that the value you found in a) will maximise profit.
3. Calculate the maximum profit.

Solution

1. In this example we are given the equation and variables to work with, which will make things a little easier.
   [latex]\scriptsize P\left( x \right)=-2{{x}^{3}}+600x+1~000[/latex]
   We can move straight onto the step where we find the derivative and equate it to zero to solve for the x-value that will maximise profit.
   .
   [latex]\scriptsize \begin{align*}{P}'\left( x \right) & =-6{{x}^{2}}+600\\{P}'\left( x \right) & =0\\-6{{x}^{2}}+600 & =0\\{{x}^{2}} & =100\\x & =\pm 10\\\therefore x & =10\end{align*}[/latex]
   .
   Since [latex]\scriptsize x[/latex] represents employees, it cannot be negative and we only accept the positive solution for the number of employees that will maximise profit.
2. To check that [latex]\scriptsize x=10[/latex] maximises profit we must find [latex]\scriptsize {P}''(10)[/latex].
   [latex]\scriptsize \begin{align*}{P}'\left( x \right)&=-6{{x}^{2}}+600\\{P}''(x)&=-12x\\{P}''(10)&=-120\end{align*}[/latex]
   Since the second derivative is negative this means that [latex]\scriptsize 10[/latex] employees will maximise profit.
3. To find the maximum profit, substitute the value we found for [latex]\scriptsize x[/latex] back into the original equation, which shows the relationship between profit and employees.
   [latex]\scriptsize \begin{align*}P\left( x \right)&=-2{{x}^{3}}+600x+1~000\\P(10)&=-2{{(10)}^{3}}+600(10)+1000\\&=5000\end{align*}[/latex]
   Maximum profit is [latex]\scriptsize \displaystyle \text{R }5000[/latex] when there are [latex]\scriptsize 10[/latex] employees.

In the last example we minimise material used.

Example 4.3

The diagram below shows a closed metal cylinder with a capacity of [latex]\scriptsize 550\text{ ml}[/latex]. The volume of the cylinder is given by the formula [latex]\scriptsize V=\pi {{r}^{2}}h[/latex] where [latex]\scriptsize r[/latex] is the radius and [latex]\scriptsize h[/latex] is the height.

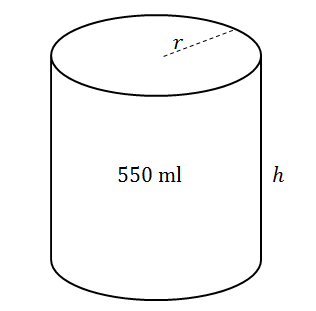
1. Express the height [latex]\scriptsize h[/latex] of the cylinder in terms of [latex]\scriptsize r[/latex].
2. Show that the surface area of cylinder can be written as [latex]\scriptsize S=2\pi {{r}^{2}}+\displaystyle \frac{{1100}}{r}[/latex].
3. Calculate the radius of the cylinder with a minimum surface area.

Solutions

1. We are given the capacity of the cylinder. When the thickness of the walls of a cylinder are insignificant, volume and capacity is basically the same thing.
   [latex]\scriptsize V=\pi {{r}^{2}}h=550[/latex]
   We must use the equation for volume to make the height the subject of the formula.
   [latex]\scriptsize \begin{align*}\pi {{r}^{2}}h&=550\\h&=\displaystyle \frac{{550}}{{\pi {{r}^{2}}}}\end{align*}[/latex]
2. For any closed container the easiest way to find the surface area is to use the formula:
   [latex]\scriptsize \text{TSA}=2\times \text{area of the base}+\text{perimeter of the base}\times h[/latex]
   Since the base of a cylinder is a circle, its area is [latex]\scriptsize \pi {{r}^{2}}[/latex] and the circumference (perimeter) is [latex]\scriptsize 2\pi r[/latex]. Substitute these formulae into the equation for total surface area and replace TSA with S.
   [latex]\scriptsize \begin{align*}S&=2\times \pi {{r}^{2}}+2\pi r\times h\\&=2\pi {{r}^{2}}+2\pi rh\end{align*}[/latex]
   Next, we need to rewrite the equation in terms of one variable only. So replace [latex]\scriptsize h[/latex] with the value you found in part a) and simplify to get the required expression.
   [latex]\scriptsize \begin{align*}S&=2\times \pi {{r}^{2}}+2\pi r\times h\\&=2\pi {{r}^{2}}+2\pi rh\\&=2\pi {{r}^{2}}+2\pi r\left( {\displaystyle \frac{{550}}{{\pi {{r}^{2}}}}} \right)\\&=2\pi {{r}^{2}}+\displaystyle \frac{{1\text{ }100}}{r}\end{align*}[/latex]
3. Calculate the radius of the cylinder with a minimum surface area.
   To find a minimum value we need to find the derivative. In this case, we need to minimise the surface area of material needed.
   [latex]\scriptsize \begin{align*}S&=2\pi {{r}^{2}}+1\text{ }100{{r}^{{-1}}}\\{S}'&=4\pi r-1\text{ }100{{r}^{{-2}}}\end{align*}[/latex]
   Note: we have changed to a negative exponent to get rid of the variable in the denominator before deriving, as you were shown in unit 3.
   .
   For a minimum value [latex]\scriptsize {S}'(r)=0[/latex]
   [latex]\scriptsize \begin{align*}4\pi r-1\text{ }100{{r}^{{-2}}}&=0\\4\pi r&=\displaystyle \frac{{1100}}{{{{r}^{2}}}}\\4\pi {{r}^{3}}&=1\text{ }100\\{{r}^{3}}&=\displaystyle \frac{{1\text{ }100}}{{4\pi }}\\r&=\sqrt[3]{{\displaystyle \frac{{275}}{\pi }}}\\&=4.44\end{align*}[/latex]
   A radius of [latex]\scriptsize 4.44[/latex] units will produce a cylinder with a minimum surface area, in other words, using the least material.

Exercise 4.1

1. The volume of a rectangular box is given by the equation [latex]\scriptsize f(x)={{x}^{3}}-8{{x}^{2}}+5x+50[/latex]. Calculate the value of [latex]\scriptsize x[/latex] for which the volume is a maximum.
2. The dimensions of a cylinder are such that [latex]\scriptsize \displaystyle r+h=12[/latex]. Determine the value of [latex]\scriptsize r[/latex] if the volume of the cylinder is at its maximum.
   HINT: [latex]\scriptsize \displaystyle V=\pi {{r}^{2}}h[/latex]
3. The radius of the base of a solid metal cylinder is [latex]\scriptsize \displaystyle x\text{ mm}[/latex] while its height is [latex]\scriptsize \displaystyle \left( {300-x} \right)\text{ mm}[/latex].
   Find the value of [latex]\scriptsize x[/latex] which results in a maximum volume if the volume is given by [latex]\scriptsize V=300\pi {{x}^{2}}-\pi {{x}^{3}}[/latex].

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to use the largest and smallest values of a function to maximise and minimise real life problems.
• How to derive to find the optimal solutions.
• How to check if your solutions are maximum or minimum values.

Unit 4: Assessment

Suggested time to complete: 30 minutes

1. The sum of two positive numbers is [latex]\scriptsize 10[/latex]. One of the numbers is multiplied by the square of the other. If each number is greater than zero, find the numbers that make this product a maximum.
2. A cat climbs into a rectangular box without a lid. The box is made of cardboard of insignificant thickness. The sides of the base are [latex]\scriptsize \displaystyle 2x\text{ cm}[/latex] by [latex]\scriptsize \displaystyle 3x\text{ cm}[/latex], and the height is [latex]\scriptsize \displaystyle h\text{ cm}[/latex].
   
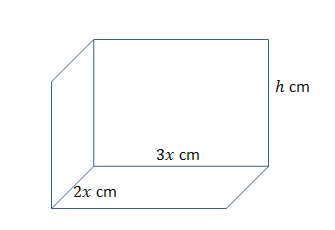
   1. If the total external surface area is [latex]\scriptsize 200\text{ c}{{\text{m}}^{2}}[/latex], show that [latex]\scriptsize \displaystyle h=\displaystyle \frac{{20}}{x}-\displaystyle \frac{{3x}}{5}[/latex].
   2. Find the dimensions of the box that will maximise the volume.
3. You need to build a fence around an area of [latex]\scriptsize 200\text{ m}[/latex]. What are the dimensions of a rectangular fence that will minimise the amount of material needed?

The full solutions are at the end of the unit.

Unit 4: Solutions

Exercise 4.1

1. .
   [latex]\scriptsize {f}'(x)=3{{x}^{2}}-16x+5[/latex]
   To find the maximum/minimum let [latex]\scriptsize {f}'(x)=0[/latex].
   [latex]\scriptsize \displaystyle \begin{align*}{f}'(x)&=3{{x}^{2}}-16x+5=0\\\therefore (3x-1)(x-5)&=0\\\therefore x&=\displaystyle \frac{1}{3}\text{ or }x=5\end{align*}[/latex]
   For maximum volume [latex]\scriptsize {{f}'}'(x) \lt 0[/latex]
   [latex]\scriptsize \begin{align*}{{f}'}'(x)&=6x-16\\{{f}'}'(\displaystyle \frac{1}{3})&=6(\displaystyle \frac{1}{3})-16\\&=-14\\&\therefore {{f}'}'(\displaystyle \frac{1}{3}) \lt 0\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}{{f}'}'(5)&=6(5)-16\\&=14\\&\therefore {{f}'}'(5) \gt 0\end{align*}[/latex]
   Maximum volume when [latex]\scriptsize x=\displaystyle \frac{1}{3}[/latex].
2. .
   [latex]\scriptsize \displaystyle \begin{align*}r+h&=12\\\therefore h&=12-r\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}V&=\pi {{r}^{2}}h\\&=\pi {{r}^{2}}(12-r)\\&=12\pi {{r}^{2}}-\pi {{r}^{3}}\end{align*}[/latex]
   For the maximum volume find the derivative with respect to [latex]\scriptsize r[/latex] and equate to zero.
   [latex]\scriptsize \displaystyle \begin{align*}{V}'&=24\pi r-3\pi {{r}^{2}}=0\\\therefore 3\pi r(8-r)&=0\\\therefore r&=0\ \text{n/a}\ \text{or}\ r=8\\\therefore r&=8\end{align*}[/latex]
3. .
   [latex]\scriptsize \displaystyle \begin{align*}{V}'&=600\pi x-3\pi {{x}^{2}}=0\\\therefore 3\pi x(200-x)&=0\\\therefore x&=0\text{ n/a or}\ x=200\\\therefore x&=200\end{align*}[/latex]

Back to Exercise 4.1

Unit 4: Assessment

1. Let the two numbers be [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] and the product be [latex]\scriptsize P[/latex].
   [latex]\scriptsize x+y=10...\text{(1)}[/latex]
   [latex]\scriptsize P=x\times {{y}^{2}}...\text{(2)}[/latex]
   .
   Make [latex]\scriptsize y[/latex] the subject of equation (1) and substitute into equation (2).
   [latex]\scriptsize y=10-x...\text{(1)}[/latex]
   [latex]\scriptsize \displaystyle \begin{align*}P&=x\times {{y}^{2}}\\&=x{{(10-x)}^{2}}\\&=x(100-20x+{{x}^{2}})\\&=100x-20{{x}^{2}}+{{x}^{3}}\end{align*}[/latex]
   Differentiate with respect to [latex]\scriptsize x[/latex].
   [latex]\scriptsize \displaystyle {P}'(x)=100-40x+3{{x}^{2}}[/latex]
   Find the value of [latex]\scriptsize x[/latex] which makes [latex]\scriptsize P[/latex] a maximum by setting the derivative equal to zero.
   [latex]\scriptsize \displaystyle \begin{align*}{P}'(x)&=3{{x}^{2}}-40x+100\\0&=(3x-10)(x-10)\\\therefore x&=\displaystyle \frac{{10}}{3}\text{ or }x=10\end{align*}[/latex]
   Substitute values into equation (1) to solve for [latex]\scriptsize y[/latex]:
   If [latex]\scriptsize \displaystyle x=10[/latex]
   [latex]\scriptsize \begin{align*}y&=10-(10)\\&=0\end{align*}[/latex]
   This is not possible since each number is greater than zero.
   .
   If [latex]\scriptsize \displaystyle x=\displaystyle \frac{{10}}{3}[/latex]
   [latex]\scriptsize \begin{align*}y&=10-(\displaystyle \frac{{10}}{3})\\&=\displaystyle \frac{{20}}{3}\end{align*}[/latex]
   Therefore, the product is maximised when the two numbers are [latex]\scriptsize \displaystyle \displaystyle \frac{{10}}{3}[/latex] and [latex]\scriptsize \displaystyle \frac{{20}}{3}[/latex].
2. .
   1. Since the box has no lid the formula for surface area becomes:
      [latex]\scriptsize \text{TSA}=\text{area of the base}+\text{perimeter of the base}\times h[/latex]
      [latex]\scriptsize \displaystyle \begin{align*}200&=2x\cdot 3x+2(2x+3x)\cdot h\\&=6{{x}^{2}}+10xh\\200-6{{x}^{2}}&=10xh\\\displaystyle \frac{{200-6{{x}^{2}}}}{{10x}}&=h\\\displaystyle \frac{{20}}{x}-\displaystyle \frac{3}{5}x&=h\end{align*}[/latex]
   2. [latex]\scriptsize \text{Volume }\!\!~\!\!\text{ =length }\!\!~\!\!\text{ }\times \text{breadth}\times \text{height}[/latex]
      [latex]\scriptsize \begin{align*}V&=2x\cdot 3x\cdot h\\&=6{{x}^{2}}h\end{align*}[/latex]
      Substitute the value for [latex]\scriptsize h[/latex] found in part a).
      [latex]\scriptsize \begin{align*}V&=6{{x}^{2}}(\displaystyle \frac{{20}}{x}-\displaystyle \frac{3}{5}x)\\&=120x-\displaystyle \frac{{18}}{5}{{x}^{3}}\end{align*}[/latex]
      For maximum:
      [latex]\scriptsize \begin{align*}{V}' & =0\\{V}' & =120-\displaystyle \frac{{54}}{5}{{x}^{2}}\\120-\displaystyle \frac{{54}}{5}{{x}^{2}} & =0\\\displaystyle \frac{{54}}{5}{{x}^{2}} & =120\\{{x}^{2}} & =\displaystyle \frac{{100}}{9}\\\therefore x & =\displaystyle \frac{{10}}{3}\end{align*}[/latex]
      Substitute back into part a) to find [latex]\scriptsize h[/latex].
      [latex]\scriptsize \begin{align*}h&=\displaystyle \frac{{20}}{{(\displaystyle \frac{{10}}{3})}}-\displaystyle \frac{{3\left( {\displaystyle \frac{{10}}{3}} \right)}}{5}\\&=4\text{ cm}\end{align*}[/latex]
      Sides are:
      [latex]\scriptsize 2(\displaystyle \frac{{10}}{3})=\displaystyle \frac{{20}}{3}\text{ cm}[/latex] and [latex]\scriptsize 3(\displaystyle \frac{{10}}{3})=10\text{ cm}[/latex]
      Dimensions for the box to have a maximum volume are [latex]\scriptsize \displaystyle \frac{{20}}{3}\text{ cm}[/latex], [latex]\scriptsize 10\text{ cm}[/latex] and [latex]\scriptsize 4\text{ cm}[/latex].
3. Let the length be [latex]\scriptsize x[/latex] and the width be [latex]\scriptsize y[/latex].
   [latex]\scriptsize \begin{align*}\text{Area } & \text{= }x\times y\\xy & =200\\\therefore y & =\displaystyle \frac{{200}}{x}\end{align*}[/latex]
   To find the amount of material for the fence find the perimeter.
   [latex]\scriptsize \begin{align*}\text{P}&=2(x+y)\\&=2x+2y\end{align*}[/latex]
   Substitute the y-value from the Area equation.
   [latex]\scriptsize \begin{align*}P&=2x+2(\displaystyle \frac{{200}}{x})\\&=2x+\displaystyle \frac{{400}}{x}\end{align*}[/latex]
   Derive and solve for the minimum x-value.
   [latex]\scriptsize \begin{align*}P&=2x+400{{x}^{{-1}}}\\{P}'&=2-400{{x}^{{-2}}}\\2-\displaystyle \frac{{400}}{{{{x}^{2}}}}&=0\\2{{x}^{2}}-400&=0\\{{x}^{2}}&=200\\x&=\pm 10\sqrt{2}\\\end{align*}[/latex]
   Since dimension is positive
   [latex]\scriptsize \displaystyle \begin{align*}x & =10\sqrt{2}\\ & =14.14\text{ m}\\\therefore y & =\displaystyle \frac{{200}}{{10\sqrt{2}}}\\ & =14.14\text{ m}\end{align*}[/latex]
   Dimensions of a rectangular fence that will minimise the amount of material needed are [latex]\scriptsize \displaystyle 14.14\text{ m}[/latex] by [latex]\scriptsize \displaystyle 14.14\text{ m}[/latex].

Back to Unit 4: Assessment