Unit outcomes

By the end of this unit you will be able to:

• Understand when to use the quadratic formula to solve quadratic equations.
• Apply the quadratic formula when necessary.

What you should know

Before you start this unit, make sure you can:

• Solve a quadratic equation by completing the square. Refer to unit 2 in this subject outcome if you need help with this.

Here is a short self-assessment to make sure you have the skills you need to proceed with this unit.

Complete the square of the following quadratic expressions:

1. [latex]\scriptsize {{x}^{2}}-4x-4=0[/latex]
2. [latex]\scriptsize 2{{x}^{2}}=6x-1[/latex]

Solutions

1. .
   [latex]\scriptsize \begin{align*}{{x}^{2}}-4x-4 & =0\\\therefore {{x}^{2}}-4x+4-4-4 & =0\\\therefore {{(x-2)}^{2}}-8 & =0\\\therefore {{(x-2)}^{2}} & =8\\\therefore (x-2) & =\pm \sqrt{8}\\\therefore x & =2\pm \sqrt{8}\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}2{{x}^{2}} & =6x-1\\\therefore 2{{x}^{2}}-6x & =1\\\therefore 2({{x}^{2}}-3x) & =1\\\therefore {{x}^{2}}-3x & =\displaystyle \frac{1}{2}\\\therefore {{x}^{2}}-3x+\displaystyle \frac{9}{4} & =\displaystyle \frac{1}{2}+\displaystyle \frac{9}{4}\\\therefore {{\left( {x-\displaystyle \frac{3}{2}} \right)}^{2}} & =\displaystyle \frac{{11}}{4}\\\therefore x-\displaystyle \frac{3}{2} & =\displaystyle \frac{{\pm \sqrt{{11}}}}{2}\\\therefore x & =\displaystyle \frac{{3\pm \sqrt{{11}}}}{2}\end{align*}[/latex]

Introduction

Completing the square is a powerful technique that can be used to factorise any quadratic expression and hence solve any quadratic equation. In fact, it is so powerful that it can even be used to create a general formula with which any quadratic equation can be solved. This formula is known as the quadratic formula.

However, the quadratic formula is not just a useful tool for finding the roots of any quadratic equation. It can also be used to predict what kind of roots these will be. Will there be two distinct roots or will the roots be the same? Will the roots be real numbers or complex numbers?

The quadratic formula can, therefore, be used to determine where, or even if, a quadratic function cuts the x-axis.

Did you know?

Quadratic equations have been around for a long time and the quadratic formula has a long history. Its development is a wonderful example of how civilisations across time have contributed to the body of knowledge we have inherited today.

The ancient Egyptians solved quadratic equations geometrically. Diophantus (250 AD) started to solve them algebraically which was further developed by the Indian mathematician Brahmagupta (597–668 AD) who described a version of the quadratic formula in words. Incidentally, Brahmagupta was also the first known mathematician to give rules for computing with zero.

In the 9th century, the highly influential Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī (depicted in Figure 1) presented the first systematic solution to linear and quadratic equations.

A more modern form of the quadratic formula (which covers all possible cases) was first discovered/invented (depending on your view) by Simon Stevin in 1594. Finally, in 1637, René Descartes published the form of the formula we use today.

The quadratic formula

The quadratic formula can be easily derived by completing the square of the standard form of the quadratic equation. Before reading on and looking at the derivation, see if you can do it yourself.

Complete the square to solve for [latex]\scriptsize x[/latex] in terms of a, [latex]\scriptsize b[/latex] and [latex]\scriptsize c[/latex] in [latex]\scriptsize a{{x}^{2}}+bx+c=0[/latex].

Here is the full derivation of the quadratic formula by completing the square.
[latex]\scriptsize \begin{align*}a{{x}^{2}}+bx+c & =0\\\therefore a{{x}^{2}}+bx & =-c\\\therefore a\left( {{{x}^{2}}+\displaystyle \frac{b}{a}x} \right) & =-c\\\therefore {{x}^{2}}+\displaystyle \frac{b}{a}x & =-\displaystyle \frac{c}{a}\quad \left[ {\displaystyle \frac{1}{2}\times \displaystyle \frac{b}{a}=\displaystyle \frac{b}{{2a}}\text{. }{{{\left( {\displaystyle \frac{b}{{2a}}} \right)}}^{2}}=\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}} \right]\\\therefore {{x}^{2}}+\displaystyle \frac{b}{a}x+\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}} & =\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}-\displaystyle \frac{c}{a}\\\therefore {{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}} & =\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}-\displaystyle \frac{{4ac}}{{4{{a}^{2}}}}\\\therefore {{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}} & =\displaystyle \frac{{{{b}^{2}}-4ac}}{{4{{a}^{2}}}}\\\therefore x+\displaystyle \frac{b}{{2a}} & =\displaystyle \frac{{\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\end{align*}[/latex]

Note: We can write both roots separately if we want to.

[latex]\scriptsize x=\displaystyle \frac{{-b+\sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\text{ or }x=\displaystyle \frac{{-b-\sqrt{{{{b}^{2}}-4ac}}}}{{2a}}[/latex]

The quadratic formula is really easy to use. You simply substitute values for [latex]\scriptsize a[/latex], [latex]\scriptsize b[/latex] and [latex]\scriptsize c[/latex] into the formula. The formula will work for any quadratic equation, even those that can be easily factorised. However, solving quadratic equations by factorisation is still the simplest and quickest method. So, use factorisation whenever you can.

Example 3.1

Solve for [latex]\scriptsize x[/latex] using the quadratic formula and check your answer by factorisation:
[latex]\scriptsize {{x}^{2}}-7x+6=0[/latex]

Solution

[latex]\scriptsize {{x}^{2}}-7x+6=0[/latex]. The equation is in standard form. Therefore, [latex]\scriptsize a=1[/latex], [latex]\scriptsize b=-7[/latex] and [latex]\scriptsize c=6[/latex].

[latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(-7)\pm \sqrt{{{{{(-7)}}^{2}}-4(1)(6)}}}}{{2(1)}}\\ & =\displaystyle \frac{{7\pm \sqrt{{49-24}}}}{2}\\&=\displaystyle \frac{{7\pm \sqrt{{25}}}}{2}\\&=\displaystyle \frac{{7\pm 5}}{2}\\\therefore x=6\text{ } & \text{or }x=1\end{align*}[/latex]

We can easily solve the quadratic equation by factorising the original quadratic expression as follows:
[latex]\scriptsize \begin{align*}{{x}^{2}}-7x+6 & =0\\\therefore (x-6)(x-1) & =0\\\therefore x=6\text{ } & \text{or }x=1\end{align*}[/latex]

Example 3.2

Solve for [latex]\scriptsize x[/latex] using the quadratic formula, leaving your answer in simplest surd form:
[latex]\scriptsize 4{{x}^{2}}=5x+13[/latex]

Solution

The equation is not yet in standard form.
[latex]\scriptsize \begin{align*}4{{x}^{2}} & =5x+13\\\therefore 4{{x}^{2}}-5x-13 & =0\end{align*}[/latex]
[latex]\scriptsize a=4[/latex], [latex]\scriptsize b=-5[/latex], [latex]\scriptsize c=-13[/latex]

Now we can solve for [latex]\scriptsize x[/latex] by using the quadratic formula.

[latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(-5)\pm \sqrt{{{{{(-5)}}^{2}}-4(4)(-13)}}}}{{2(4)}}\\&=\displaystyle \frac{{5\pm \sqrt{{25+208}}}}{8}\\&=\displaystyle \frac{{5\pm \sqrt{{233}}}}{8}\\\therefore x=\displaystyle \frac{{5+\sqrt{{233}}}}{8}\text{ } & \text{or }x=\displaystyle \frac{{5-\sqrt{{233}}}}{8}\end{align*}[/latex]

We cannot simplify these roots any further. They are in simplest surd form.

Example 3.3

Solve for [latex]\scriptsize x[/latex] using the quadratic formula, leaving your answer in simplest surd form:
[latex]\scriptsize 8x-21=3{{x}^{2}}[/latex]

Solution

The equation is not in standard form.
[latex]\scriptsize \begin{align*}8x-21 & =3{{x}^{2}}\\\therefore -3{{x}^{2}}+8x-21 & =0\end{align*}[/latex]

You can decide whether to proceed with the equation above where [latex]\scriptsize a=-3[/latex] or to multiply both sides by [latex]\scriptsize -1[/latex] to make [latex]\scriptsize a \gt 0[/latex]. You will get the same result. Let’s proceed with [latex]\scriptsize a=-3[/latex].

[latex]\scriptsize a=-3[/latex], [latex]\scriptsize b=8[/latex], [latex]\scriptsize c=-21[/latex]

Now we can solve for [latex]\scriptsize x[/latex] by using the quadratic formula.

[latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(8)\pm \sqrt{{{{{(8)}}^{2}}-4(-3)(-21)}}}}{{2(-3)}}\\&=\displaystyle \frac{{-8\pm \sqrt{{64-252}}}}{{-6}}\\&=\displaystyle \frac{{8\pm \sqrt{{-188}}}}{6}\end{align*}[/latex]
Therefore, [latex]\scriptsize x[/latex] has no real solution.

In this case we end up with a negative number under the square root sign. Therefore, the roots to this quadratic equation are not real. They are complex.

Exercise 3.1

1. Solve for the unknown in each case using the quadratic equation, leaving your answer in simplest surd form:
   1. [latex]\scriptsize {{x}^{2}}-9x+2=0[/latex]
   2. [latex]\scriptsize -2{{f}^{2}}+3f=-2[/latex]
   3. [latex]\scriptsize {{y}^{2}}=7(3-2y)[/latex]
   4. [latex]\scriptsize 2{{x}^{2}}=12x[/latex]
   5. [latex]\scriptsize 6{{x}^{2}}=7[/latex]
2. Solve for [latex]\scriptsize x[/latex] using the quadratic equation and round your solution(s) to two decimal places: [latex]\scriptsize 3{{x}^{2}}+7x=21[/latex]

The full solutions are at the end of the unit.

The nature of roots

Please note that this section on the nature of roots is not technically part of the NC(V) level 3 curriculum. However, it has been included here as a helpful addition to students’ knowledge about the roots of quadratic equations and how these directly relate to the kinds of intercepts that quadratic functions make with the x-axis.

As we said in the introduction to this unit, the quadratic formula can be used to not only calculate the roots of a quadratic equation but also predict what kind of roots they are. This can be very useful when dealing with quadratic functions.

There is one part of the quadratic formula that does this. It is the portion under the square root sign and is called the discriminant. It is sometimes given the symbol [latex]\scriptsize \Delta[/latex] (delta), the Greek letter ‘d’.

Therefore, [latex]\scriptsize \Delta ={{b}^{2}}-4ac[/latex] (the discriminant).

If [latex]\scriptsize \Delta \gt 0[/latex], then the number under the square root is positive and the roots of the equation are distinct (different), and both are real numbers.

[latex]\scriptsize x=\displaystyle \frac{{-3\pm \sqrt{{27}}}}{2}[/latex]
[latex]\scriptsize \Delta =27[/latex] and the roots are [latex]\scriptsize x=\displaystyle \frac{{-3+\sqrt{{27}}}}{2}\text{ or }\displaystyle \frac{{-3-\sqrt{{27}}}}{2}[/latex] (the roots are distinct and real numbers)

If [latex]\scriptsize \Delta \lt 0[/latex], then the number under the square root sign is negative and the roots of the equation are distinct, and both are complex (non-real) numbers.

[latex]\scriptsize x=\displaystyle \frac{{-3\pm \sqrt{{-27}}}}{2}[/latex]
[latex]\scriptsize \Delta =-27[/latex] and the roots are [latex]\scriptsize x=\displaystyle \frac{{-3+\sqrt{{-27}}}}{2}\text{ or }\displaystyle \frac{{-3-\sqrt{{-27}}}}{2}[/latex] (the roots are distinct and complex (non-real) numbers)

If [latex]\scriptsize \Delta =0[/latex], then the roots are real and equal.

[latex]\scriptsize x=\displaystyle \frac{{-3\pm \sqrt{0}}}{2}[/latex]
[latex]\scriptsize \Delta =0[/latex] and the roots are [latex]\scriptsize x=\displaystyle \frac{{-3+\sqrt{0}}}{2}=-\displaystyle \frac{3}{2}\text{ or }\displaystyle \frac{{-3-\sqrt{{-27}}}}{2}=-\displaystyle \frac{3}{2}[/latex] (the roots are the same and real numbers)

There is a graphical interpretation of this as well. In the context of the quadratic function [latex]\scriptsize f(x)=a{{x}^{2}}+bx+c[/latex], when we solve the quadratic equation [latex]\scriptsize a{{x}^{2}}+bx+c=0[/latex] we are really finding the x-intercepts of the function.

If [latex]\scriptsize \Delta \gt 0[/latex], then the roots are distinct and real. Therefore, the function has two x-intercepts (figure 2).

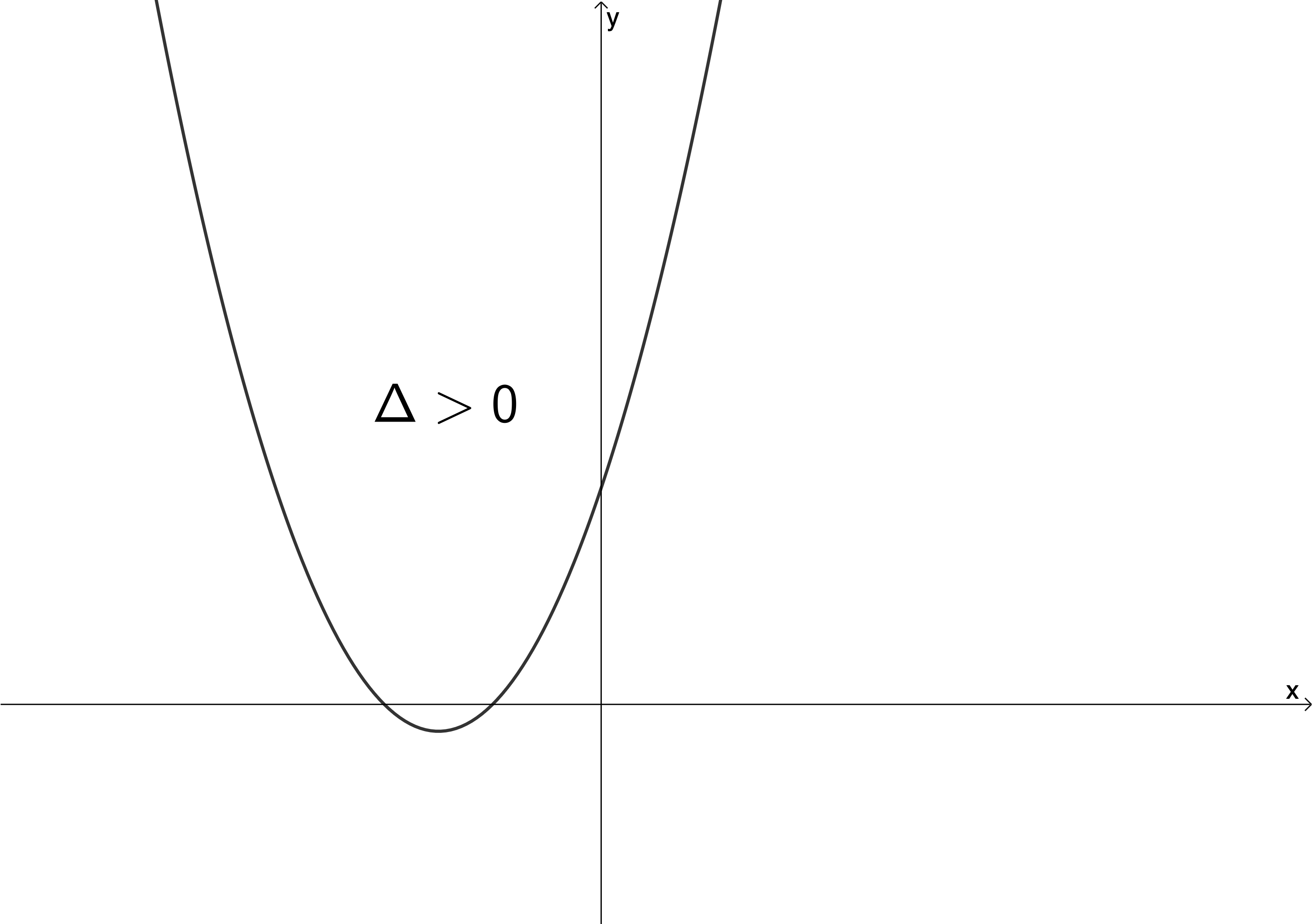
If [latex]\scriptsize \Delta \lt 0[/latex], then the roots are distinct and complex (non-real). Therefore, the function has no x-intercepts.

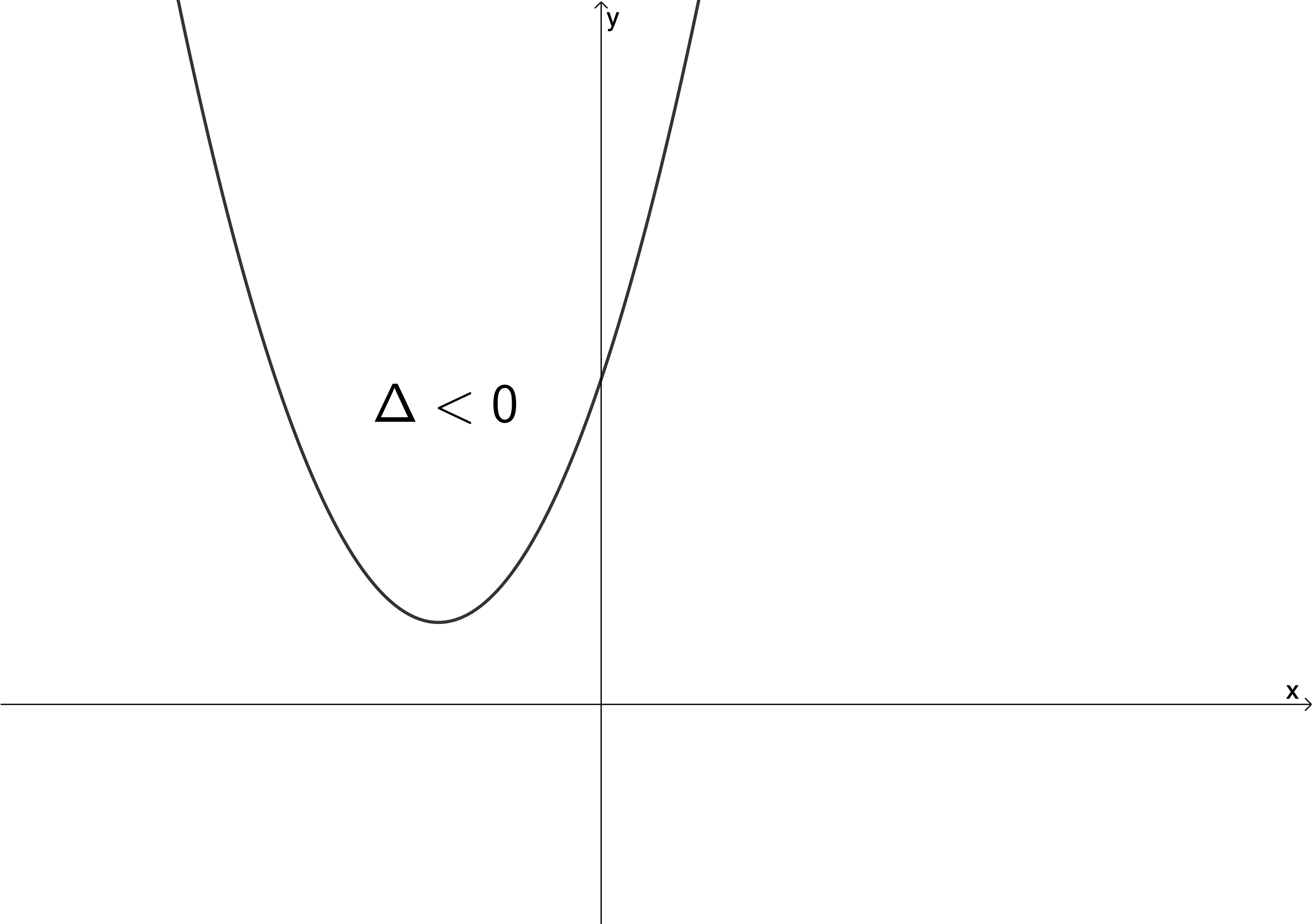
If [latex]\scriptsize \Delta =0[/latex], then the roots are real and equal. This means the function just touches the x-axis at one point.

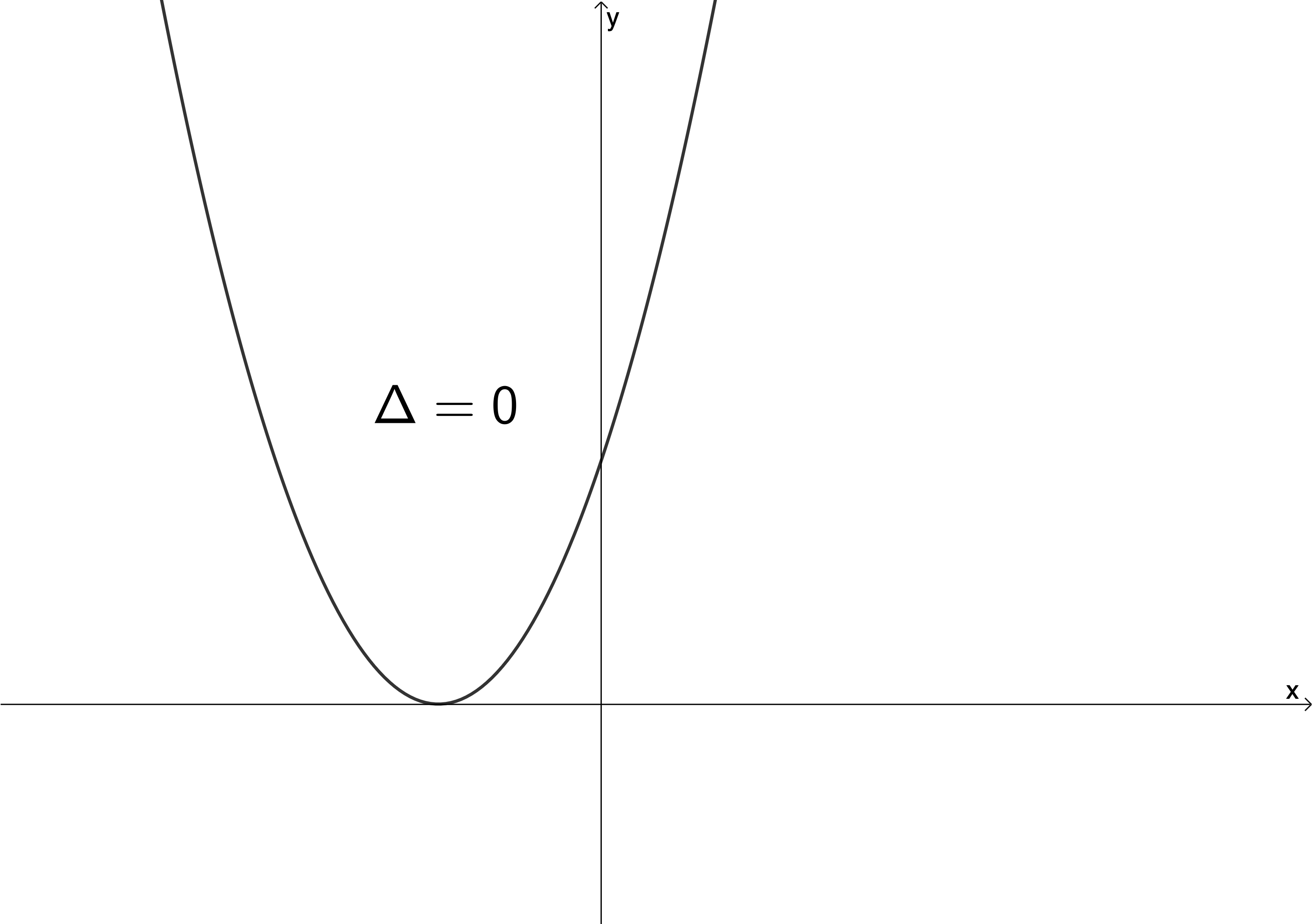
Take note!

[latex]\scriptsize \Delta ={{b}^{2}}-4ac[/latex]

If [latex]\scriptsize \Delta \gt 0[/latex], the roots are distinct and real.
If [latex]\scriptsize \Delta \lt 0[/latex], the roots are distinct and complex (non-real).
If [latex]\scriptsize \Delta =0[/latex], the roots are the same and real.

The discriminant only tells you about the kind of roots. It does not tell you what these roots are.

Exercise 3.2

Determine the nature of the roots for the following quadratic equations:

1. [latex]\scriptsize {{x}^{2}}+2x+2[/latex]
2. [latex]\scriptsize 3{{x}^{3}}=6x+1[/latex]
3. [latex]\scriptsize -2{{x}^{2}}=0[/latex]
4. [latex]\scriptsize 7x-4=5{{x}^{2}}[/latex]

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to solve quadratic equations using the quadratic formula.
• How to determine the nature of the roots of a quadratic equation by evaluating the discriminant (additional information).

Unit 3: Assessment

Suggested time to complete: 50 minutes

1. Solve for the unknown in each of the following by factorisation if possible, leaving your answer in simplest surd form where necessary:
   1. [latex]\scriptsize -4{{x}^{2}}-41x-45=0[/latex]
   2. [latex]\scriptsize 3{{a}^{2}}+10a-48=0[/latex]
   3. [latex]\scriptsize 63-5{{g}^{2}}=26g[/latex]
   4. [latex]\scriptsize x(x-8)+14=0[/latex]
   5. [latex]\scriptsize \displaystyle \frac{{3x}}{{(x-3)}}-\displaystyle \frac{{2x}}{{(x+4)}}=\displaystyle \frac{3}{{{{x}^{2}}+x-12}}[/latex]
   6. [latex]\scriptsize 2x\left( {x-\displaystyle \frac{5}{2}} \right)-5=-\displaystyle \frac{5}{{2{{x}^{2}}-5x}}[/latex]

Question 2 is adapted from Everything Maths Grade 11 Exercise 2-11 question 22.

2. .
   1. Solve for [latex]\scriptsize x[/latex] in [latex]\scriptsize {{x}^{2}}-6=x[/latex].
   2. Hence solve for [latex]\scriptsize y[/latex] in [latex]\scriptsize {{(y-7)}^{2}}=y-1[/latex].
3. Solve for [latex]\scriptsize x[/latex] in [latex]\scriptsize 2{{({{x}^{2}}+3)}^{{\frac{1}{2}}}}=9[/latex].

The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

1. .
   1. .
      [latex]\scriptsize \begin{align*}{{x}^{2}}-9x+2 & =0\\a=1,b & =-9,c=2\\x&=\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(-9)\pm \sqrt{{{{{(-9)}}^{2}}-4(1)(2)}}}}{{2(1)}}\\&=\displaystyle \frac{{9\pm \sqrt{{81-8}}}}{2}\\&=\displaystyle \frac{{9\pm \sqrt{{73}}}}{2}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}-2{{f}^{2}}+3f & =-2\\\therefore -2{{f}^{2}}+3f+2 & =0\\\therefore 2{{f}^{2}}-3f-2 & =0\\a=2,b=-3,c=-2 & \\f & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}} & \\\therefore f & =\displaystyle \frac{{-(-3)\pm \sqrt{{{{{(-3)}}^{2}}-4(2)(-2)}}}}{{2(2)}}\\&=\displaystyle \frac{{3\pm \sqrt{{9+16}}}}{4}\\&=\displaystyle \frac{{3\pm \sqrt{{25}}}}{4}\\\therefore f=\displaystyle \frac{{3+5}}{4}=2\text{ } & \text{or }f=\displaystyle \frac{{3-5}}{4}=-\displaystyle \frac{1}{2}\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}{{y}^{2}} & =7(3-2y)\\\therefore {{y}^{2}} & =21-14y\\\therefore {{y}^{2}}+14y-21 & =0\\a=1,b=14,c=-21 & \end{align*}[/latex]
      [latex]\scriptsize \begin{align*}y&=\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore y & =\displaystyle \frac{{-(14)\pm \sqrt{{{{{(14)}}^{2}}-4(1)(-21)}}}}{{2(1)}}\\&=\displaystyle \frac{{-14\pm \sqrt{{196+84}}}}{2}\\&=\displaystyle \frac{{-14\pm \sqrt{{280}}}}{2}\\&=\displaystyle \frac{{-14\pm 2\sqrt{{70}}}}{2}\quad \sqrt{{280}}=\sqrt{{4\times 70}}=2\sqrt{{70}}\\&=-7\pm \sqrt{{70}}\end{align*}[/latex]
   4. .
      [latex]\scriptsize \begin{align*}2{{x}^{2}} & =12x\\\therefore 2{{x}^{2}}-12x & =0\\\therefore {{x}^{2}}-6x & =0\\a=1,b=-6,c=0 & \end{align*}[/latex]
      [latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(-6)\pm \sqrt{{{{{(-6)}}^{2}}-4(1)(0)}}}}{{2(1)}}\\&=\displaystyle \frac{{6\pm \sqrt{{36}}}}{2}\\\therefore x=\displaystyle \frac{{12}}{2}=6\text{ } & \text{or }x=\displaystyle \frac{0}{2}=0\end{align*}[/latex]
   5. .
      [latex]\scriptsize \begin{align*}6{{x}^{2}} & =7\\\therefore 6{{x}^{2}}-7 & =0\\a=6,b=0,c=-7 & \end{align*}[/latex]
      [latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(0)\pm \sqrt{{{{{(0)}}^{2}}-4(6)(-7)}}}}{{2(4)}}\\&=\displaystyle \frac{{\pm \sqrt{{168}}}}{8}\\&=\displaystyle \frac{{\pm 2\sqrt{{42}}}}{8}\\&=\displaystyle \frac{{\pm \sqrt{{42}}}}{4}\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}3{{x}^{2}}+7x & =21\\\therefore 3{{x}^{2}}+7x-21 & =0\\a=3,b=7,c=-21 & \end{align*}[/latex]
   [latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\&=\displaystyle \frac{{-(7)\pm \sqrt{{{{{(7)}}^{2}}-4(3)(-21)}}}}{{2(3)}}\\&=\displaystyle \frac{{-7\pm \sqrt{{49+252}}}}{6}\\&=\displaystyle \frac{{-7\pm \sqrt{{301}}}}{6}\\\therefore x=1.72\text{ } & \text{or }x=-4.06\end{align*}[/latex]

Back to Exercise 3.1

Exercise 3.2

1. .
   [latex]\scriptsize \begin{align*}{{x}^{2}}+2x+2=0\\a=1,b=2,c=2\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\Delta &={{b}^{2}}-4ac\\&={{(2)}^{2}}-4(1)(2)\\&=4-8\\&=-4\\\therefore \Delta & \lt 0\end{align*}[/latex]
   The roots are distinct and complex (non-real).
2. .
   [latex]\scriptsize \begin{align*}3{{x}^{3}}=6x+1\\\therefore 3{{x}^{2}}-6x-1=0\\a=3,b=-6,c=-1\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\Delta &={{b}^{2}}-4ac\\&={{(-6)}^{2}}-4(3)(-1)\\&=36+12\\&=48\\\therefore \Delta & \gt 0\end{align*}[/latex]
   The roots are distinct and real. The function has two real x-intercepts.
3. .
   [latex]\scriptsize \begin{align*}-2{{x}^{2}}=0\\a=-2,b=0,c=0\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\Delta &={{b}^{2}}-4ac\\&={{(0)}^{2}}-4(-2)(0)\\&=0\\\therefore \Delta & =0\end{align*}[/latex]
   The roots are the same and real. The function has one real x-intercept or touches the x-axis at one point.
4. .
   [latex]\scriptsize \begin{align*}7x-4=5{{x}^{2}}\\\therefore 5{{x}^{2}}-7x+4=0\\a=5,b=-7,c=4\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\Delta &={{b}^{2}}-4ac\\&={{(-7)}^{2}}-4(5)(4)\\&=49-80\\&=-31\\\therefore \Delta & \lt 0\end{align*}[/latex]
   The roots are distinct and complex (non-real). The function has no x-intercepts.

Back to Exercise 3.2

Unit 3: Assessment

1. .
   1. .
      [latex]\scriptsize \begin{align*}-4{{x}^{2}}-41x-45 & =0\\\therefore 4{{x}^{2}}+41x+45 & =0\\\therefore (4x+5)(x+9) & =0\\\therefore x=-\displaystyle \frac{5}{4}\text{ } & \text{or }x=-9\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}3{{a}^{2}}+10a-48 & =0\\\therefore (3a-8)(a+6) & =0\\\therefore a=\displaystyle \frac{8}{3}\text{ } & \text{or }a=-6\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}63-5{{g}^{2}} & =26g\\\therefore 5{{g}^{2}}+26g-63 & =0\\\therefore (5g-9)(g+7) & =0\\\therefore x=\displaystyle \frac{9}{5}\text{ } & \text{or }x=-7\end{align*}[/latex]
   4. .
      [latex]\scriptsize \begin{align*}x(x-8)+14=0\\\therefore {{x}^{2}}-8x+14=0\\a=1,b=-8,c=14\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(-8)\pm \sqrt{{{{{(-8)}}^{2}}-4(1)(14)}}}}{{2(1)}}\\&=\displaystyle \frac{{8\pm \sqrt{{64-56}}}}{2}\\&=\displaystyle \frac{{8\pm \sqrt{8}}}{2}\\&=\displaystyle \frac{{8\pm 2\sqrt{2}}}{2}\\&=4\pm \sqrt{2}\end{align*}[/latex]
   5. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{3x}}{{(x-3)}}-\displaystyle \frac{{2x}}{{(x+4)}} & =\displaystyle \frac{3}{{{{x}^{2}}+x-12}}\\\therefore \displaystyle \frac{{3x}}{{(x-3)}}-\displaystyle \frac{{2x}}{{(x+4)}} & =\displaystyle \frac{3}{{(x-3)(x+4)}},x\ne 3,x\ne -4\\\therefore 3x(x+4)-2x(x-3) & =3\\\therefore 3{{x}^{2}}+12x-2{{x}^{2}}+6x-3 & =0\\\therefore {{x}^{2}}+18x-3 & =0\\a=1,b=18,c=-3 & \end{align*}[/latex]
      [latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(18)\pm \sqrt{{{{{(-18)}}^{2}}-4(1)(-3)}}}}{{2(1)}}\\&=\displaystyle \frac{{-18\pm \sqrt{{324+12}}}}{2}\\&=\displaystyle \frac{{-18\pm \sqrt{{336}}}}{2}\\&=\displaystyle \frac{{-18\pm 4\sqrt{{21}}}}{2}\quad \left[ {\sqrt{{336}}=\sqrt{{16\times 21}}=4\sqrt{{21}}} \right]\\&=-9\pm 2\sqrt{{21}}\end{align*}[/latex]
   6. .
      [latex]\scriptsize \begin{align*}2x\left( {x-\displaystyle \frac{5}{2}} \right)-6 & =-\displaystyle \frac{5}{{2{{x}^{2}}-5x}}\\\therefore (2{{x}^{2}}-5x)-6 & =-\displaystyle \frac{5}{{(2{{x}^{2}}-5x)}}\\\text{Let }2{{x}^{2}}-5x=A & \\\therefore A-6 & =-\displaystyle \frac{5}{A}\\\therefore {{A}^{2}}-6A & =-5\\\therefore {{A}^{2}}-6A+5 & =0\\\therefore (A-5)(A-1) & =0\\\therefore A=5\text{ } & \text{or }A=1\\\therefore 2{{x}^{2}}-5x=5\text{ } & \text{or }2{{x}^{2}}-5x=1\\\therefore 2{{x}^{2}}-5x-5=0\text{ } & \text{or }2{{x}^{2}}-5x-1=0\end{align*}[/latex]
      .
      [latex]\scriptsize \begin{align*}&2{{x}^{2}}-5x-5=0\\&a=2,b=-5,c=-5\end{align*}[/latex]                    [latex]\scriptsize \begin{align*}&2{{x}^{2}}-5x-1=0\\&a=2,b=-5,c=-1\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(-5)\pm \sqrt{{{{{(-5)}}^{2}}-4(2)(-5)}}}}{{2(2)}}\\&=\displaystyle \frac{{5\pm \sqrt{{25+40}}}}{4}\\&=\displaystyle \frac{{5\pm \sqrt{{65}}}}{4}\end{align*}[/latex]         [latex]\scriptsize \begin{align*}x & =\displaystyle \frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\\\therefore x & =\displaystyle \frac{{-(-5)\pm \sqrt{{{{{(-5)}}^{2}}-4(2)(-1)}}}}{{2(2)}}\\&=\displaystyle \frac{{5\pm \sqrt{{25+8}}}}{4}\\&=\displaystyle \frac{{5\pm \sqrt{{33}}}}{4}\end{align*}[/latex]
2. .
   1. .
      [latex]\scriptsize \begin{align*}{{x}^{2}}-6 & =x\\\therefore {{x}^{2}}-x-6 & =0\\\therefore (x+2)(x-3) & =0\\\therefore x=-2\text{ } & \text{or }x=3\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}{{(y-7)}^{2}} & =y-1\\\therefore {{(y-7)}^{2}} & =(y-7)+6\\\therefore {{(y-7)}^{2}}-6 & =(y-7)\\\therefore (y-7)=-2\text{ } & \text{or }(y-7)=3\\\therefore y=5\text{ } & \text{or }y=10\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}2{{({{x}^{2}}+3)}^{{\frac{1}{2}}}} & =9\quad \text{Square both sides}\\\therefore 4({{x}^{2}}+3) & =81\\\therefore 4{{x}^{2}}+12-81 & =0\\\therefore 4{{x}^{2}} & =69\\\therefore {{x}^{2}} & =\displaystyle \frac{{69}}{4}\\\therefore x & =\displaystyle \frac{{\pm \sqrt{{69}}}}{2}\end{align*}[/latex]

Back to Unit 3: Assessment