Unit outcomes

By the end of this unit you will be able to:

• Manipulate and simplify algebraic expressions by completing the square.

What you should know

Before you start this unit, make sure you can:

• Manipulate and simplify algebraic expressions. Refer to level 2 subject outcome 2.2 unit 1 if you need help with this.
• Simplify algebraic expressions by means of factorisation. Refer to level 2 subject outcome 2.2 unit 2 and unit 1 in this subject outcome if you need help with this.
• Add and subtract algebraic fractions. Refer to level 2 subject outcome 2.2 unit 3 if you need help with this.

Introduction

Completing the square is a powerful technique that has many useful applications. It can be used to:

• simplify algebraic expressions
• solve quadratic equations, especially when the roots are either irrational or non-real
• find the turning point of a quadratic function by converting the quadratic function from standard form [latex]\scriptsize f(x)=a{{x}^{2}}+bx+c[/latex] into the turning point form [latex]\scriptsize f(x)=a{{(x+p)}^{2}}+q[/latex].

The technique was first developed by the great Persian mathematician and ‘Father of Algebra’ Muḥammad ibn Mūsā al-Khwārizmī as a way to solve quadratic equations that did not factorise easily.

The technique is called completing the square because it literally completes the square.

Completing the square

Suppose we have the quadratic expression [latex]\scriptsize {{x}^{2}}+6x+12[/latex]. You will notice that this quadratic does not factorise nicely at all. But we can break it up into its components and represent these visually (see Figure 1).

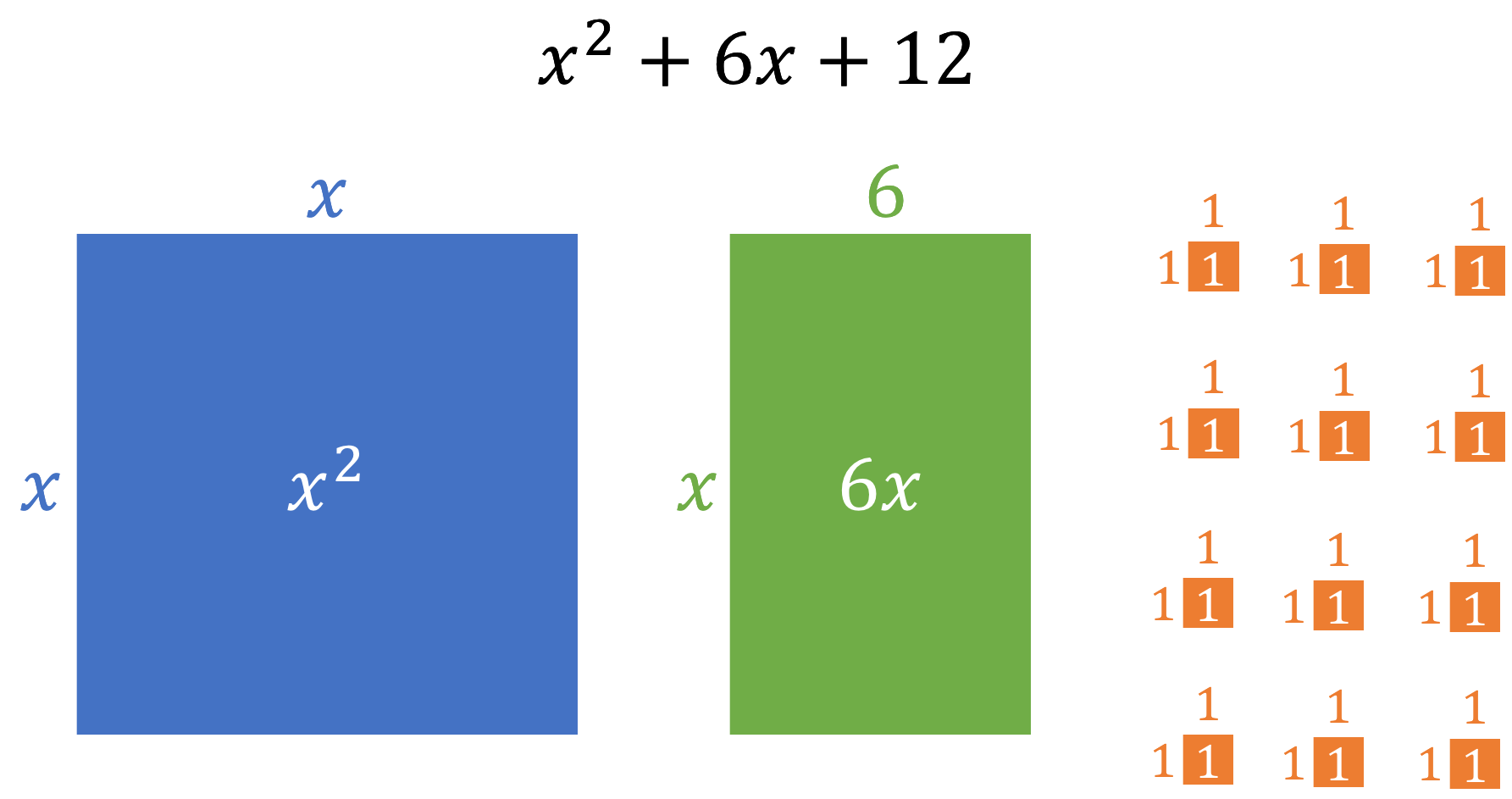
Now, if we cut the green [latex]\scriptsize 6x[/latex] rectangle in half to make two [latex]\scriptsize 3x[/latex] rectangles, we can lay these pieces as shown in Figure 2.

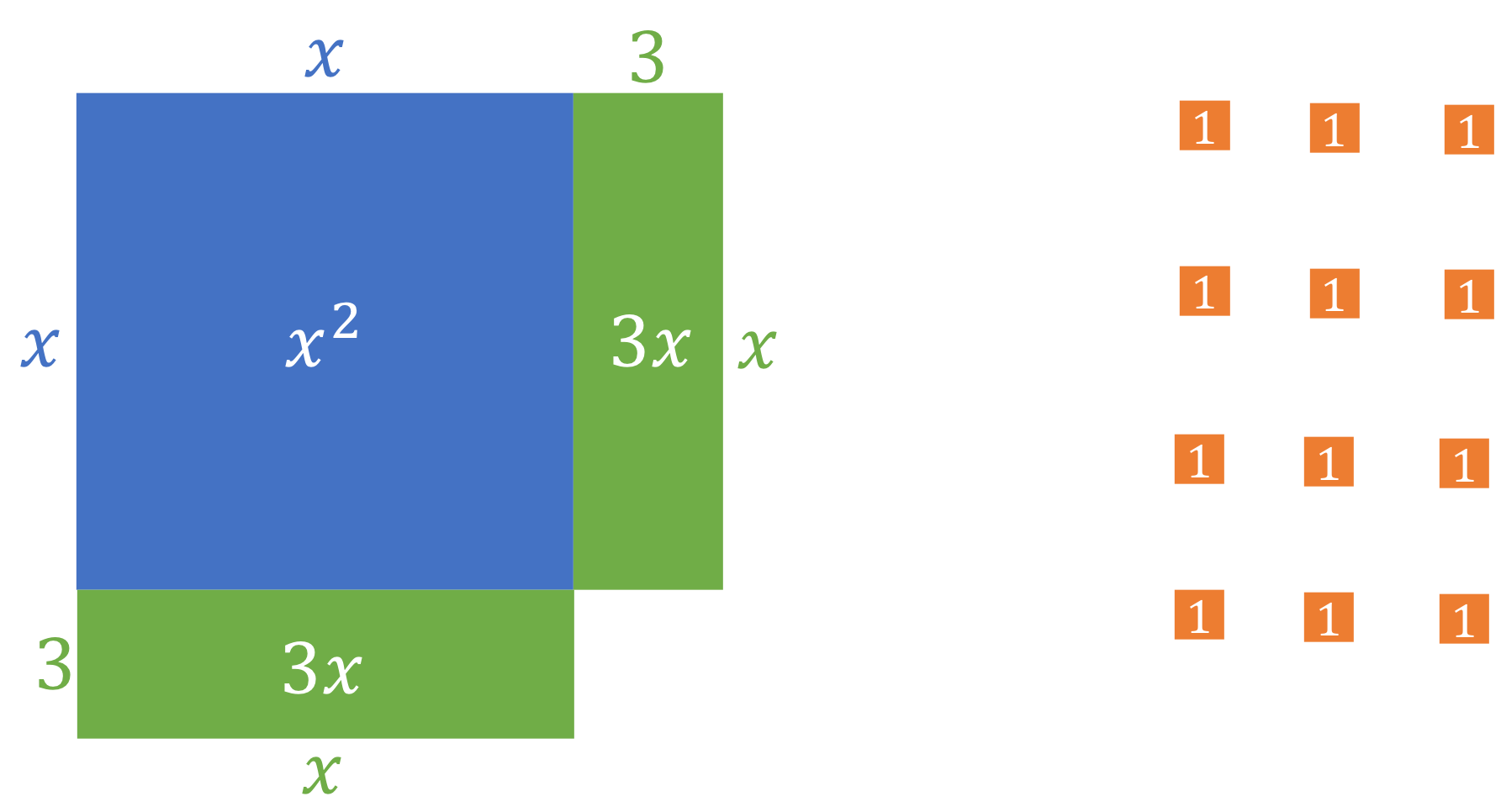
But we have a missing piece of the square that is a [latex]\scriptsize 3\times 3[/latex] hole in the bottom right-hand corner. We can fill it with nine of the [latex]\scriptsize 1\times 1[/latex] blocks (see Figure 3).

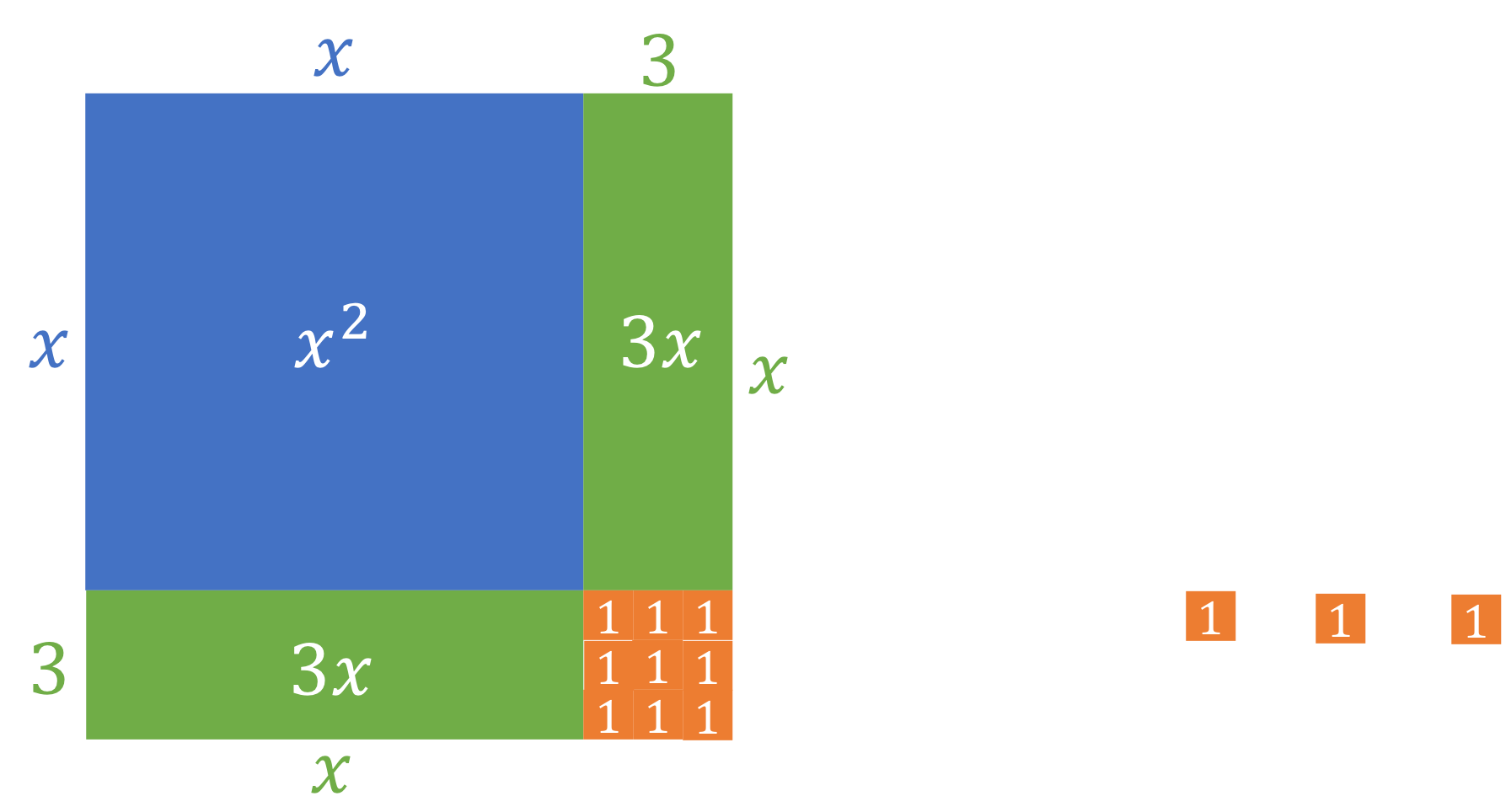
In this way we have ‘completed the square’. But what are the dimensions of this square? Well, they are [latex]\scriptsize (x+3)\times (x+3)[/latex] or [latex]\scriptsize {{(x+3)}^{2}}[/latex].

So, our original expression [latex]\scriptsize {{x}^{2}}+6x+12[/latex] can be written as [latex]\scriptsize {{(x+3)}^{2}}+3[/latex] (don’t forget the three [latex]\scriptsize 1\times 1[/latex] blocks).

Let’s have another look at what we did, but this time algebraically.

Step 1: Identify the coefficient of the [latex]\scriptsize x[/latex] term.
This is [latex]\scriptsize 6[/latex].

Step 2: Halve the coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize \displaystyle \frac{6}{2}=3[/latex]

Step 3: Square the halved coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize {{\left( {\displaystyle \frac{6}{2}} \right)}^{2}}={{3}^{2}}=9[/latex]

Step 4: Add this new term to the expression.
[latex]\scriptsize {{x}^{2}}+6x{\color{Red} +9}+12[/latex]

Step 5: To keep the value of the expression the same, subtract this new term from the expression as well.
[latex]\scriptsize {{x}^{2}}+6x{\color{Red} +9-9}+12[/latex]

Step 6: Factorise the newly created perfect square quadratic expression.
[latex]\scriptsize \begin{align*}&{\color{Magenta} {{x}^{2}}+6x+9}{\color{Red} -9}+12\\&={\color{Magenta} (x+3)(x+3)}{\color{Red} -9}+12\\&={\color{Magenta} {{(x+3)}^{2}}}{\color{Red} -9}+12\end{align*}[/latex]

In general, the constant in the squared binomial (the [latex]\scriptsize 3[/latex] in [latex]\scriptsize {{(x+3)}^{2}}[/latex] in this case) will always be half the coefficient of the [latex]\scriptsize x[/latex] term ([latex]\scriptsize \displaystyle \frac{6}{2}=3[/latex] in this case). You should also expand this squared binomial to make sure you get back to the original quadratic – [latex]\scriptsize {{(x+3)}^{2}}=(x+3)(x+3)={{x}^{2}}+6x+9[/latex].

Step 7: Collect the constants.
[latex]\scriptsize \begin{align*}&{\color{Magenta} {{x}^{2}}+6x+9}{\color{Red} -9}+12\\&={\color{Magenta} (x+3)(x+3)}{\color{Red} -9}+12\\&={\color{Magenta} {{(x+3)}^{2}}}{\color{Red} -9}+12\\&={\color{Magenta} {{(x+3)}^{2}}}+3\end{align*}[/latex]

Example 3.1

Complete the square for [latex]\scriptsize {{x}^{2}}+4x+5[/latex].

Solution

Step 1: Identify the coefficient of the [latex]\scriptsize x[/latex] term.
This is [latex]\scriptsize 4[/latex].

Step 2: Halve the coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize \displaystyle \frac{4}{2}=2[/latex]

Step 3: Square the halved coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize {{\left( {\displaystyle \frac{4}{2}} \right)}^{2}}={{2}^{2}}=4[/latex]

Step 4: Add this new term to the expression and, to keep the value of the expression the same, subtract this new term from the expression as well.
[latex]\scriptsize {{x}^{2}}+4x{\color{Red}+4-4}+5[/latex]

Step 5: Factorise the newly created perfect square quadratic expression.
[latex]\scriptsize \begin{align*}&{\color{Magenta} {{x}^{2}}+4x+4}{\color{Red} -4}+5\\&={\color{Magenta} (x+2)(x+2)}{\color{Red} -4}+5\\&={\color{Magenta} {{(x+2)}^{2}}}{\color{Red} -4}+5\end{align*}[/latex]

Step 6: Collect the constants.
[latex]\scriptsize \begin{align*}&{\color{Magenta} {{(x+2)}^{2}}}{\color{Red} -4}+5\\&={\color{Magenta} {{(x+2)}^{2}}}+1\end{align*}[/latex]

Example 3.2

Complete the square for [latex]\scriptsize {{x}^{2}}-4x+5[/latex].

Solution

Step 1: Identify the coefficient of the [latex]\scriptsize x[/latex] term.
This is [latex]\scriptsize -4[/latex].

Step 2: Halve the coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize \displaystyle \frac{{-4}}{2}=-2[/latex]

Step 3: Square the halved coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize {{\left( {\displaystyle \frac{{-4}}{2}} \right)}^{2}}={{(-2)}^{2}}=4[/latex]

Step 4: Add this new term to the expression and, to keep the value of the expression the same, subtract this new term from the expression as well.
[latex]\scriptsize {{x}^{2}}-4x{\color{Red} +4-4}+5[/latex]

Step 5: Factorise the newly created perfect square quadratic expression.
[latex]\scriptsize \begin{align*}&{\color{Magenta} {{x}^{2}}-4x+4}{\color{Red} -4}+5\\&={\color{Magenta} (x-2)(x-2)}{\color{Red} -4}+5\quad \text{Note how the perfect square quadratic factorises}\\&={\color{Magenta} {{(x-2)}^{2}}}{\color{Red} -4}+5\end{align*}[/latex]

Step 6: Collect the constants.
[latex]\scriptsize \begin{align*}&{\color{Magenta} {{(x-2)}^{2}}}{\color{Red} -4}+5\\&={\color{Magenta} {{(x-2)}^{2}}}+1\end{align*}[/latex]

Example 3.3

Complete the square for [latex]\scriptsize {{x}^{2}}-3x-5[/latex].

Solution

Step 1: Identify the coefficient of the [latex]\scriptsize x[/latex] term.
This is [latex]\scriptsize -3[/latex].

Step 2: Halve the coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize \displaystyle \frac{{-3}}{2}[/latex]

Step 3: Square the halved coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize {{\left( {\displaystyle \frac{{-3}}{2}} \right)}^{2}}=\displaystyle \frac{9}{4}[/latex]

Step 4: Add this new term to the expression and, to keep the value of the expression the same, subtract this new term from the expression as well.
[latex]\scriptsize {{x}^{2}}-3x{\color{Red} +\displaystyle \frac{9}{4}-\displaystyle \frac{9}{4}}-5[/latex]

Step 5: Factorise the newly created perfect square quadratic expression.
[latex]\scriptsize \begin{align*} {\color{Green}{x^2-3x+ \displaystyle \frac{9}{4}}}- {\color{Red}{\displaystyle \frac{9}{4}}}-5&= {\color{Green}{\left(x- \displaystyle \frac{3}{2} \right)\left(x- \displaystyle \frac{3}{2} \right)}} -{\color{Red}{\displaystyle \frac{9}{4}}}-5&& \text{Note how the perfect square quadratic factorises}\\ &= {\color{Green}{\left( x- \displaystyle \frac{3}{2} \right)^2}} {\color{Red}{-\displaystyle \frac{9}{4}}}-5\end{align*}[/latex]

Step 6: Collect the constants.
[latex]\scriptsize \begin{align*}{\color{Green} {{\left( {x-\displaystyle \frac{3}{2}} \right)}^{2}}}{\color{Red} -\displaystyle \frac{9}{4}}-5&={\color{Green} {{\left( {x-\displaystyle \frac{3}{2}} \right)}^{2}}}-\displaystyle \frac{{9-20}}{4}\\&={\color{Green} {{\left( {x-\displaystyle \frac{3}{2}} \right)}^{2}}}-\displaystyle \frac{{29}}{4}\end{align*}[/latex]

Example 3.4

Complete the square for [latex]\scriptsize 2{{x}^{2}}-3x+4[/latex].

Solution

Before we can start to complete the square, we need to get the coefficient of [latex]\scriptsize {{x}^{2}}[/latex] to be [latex]\scriptsize 1[/latex]. We need to take out a common factor of [latex]\scriptsize 2[/latex] from each term.
[latex]\scriptsize \begin{align*}&2{{x}^{2}}-3x+4\\&=2\left( {{{x}^{2}}-\displaystyle \frac{3}{2}x+2} \right)\end{align*}[/latex]

Step 1: Identify the coefficient of the [latex]\scriptsize x[/latex] term.
This is [latex]\scriptsize -\displaystyle \frac{3}{2}[/latex].

Step 2: Halve the coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize \displaystyle \frac{{\displaystyle \frac{{-3}}{2}}}{2}=-\displaystyle \frac{3}{2}\times \displaystyle \frac{1}{2}=-\displaystyle \frac{3}{4}[/latex]

Step 3: Square the halved coefficient of the [latex]\scriptsize x[/latex] term.
[latex]\scriptsize {{\left( {\displaystyle \frac{{-3}}{4}} \right)}^{2}}=\displaystyle \frac{9}{{16}}[/latex]

Step 4: Add this new term to the expression and, to keep the value of the expression the same, subtract this new term from the expression as well.
[latex]\scriptsize 2\left( {{{x}^{2}}-\displaystyle \frac{3}{2}x{\color{Red} +\displaystyle \frac{9}{{16}}-\displaystyle \frac{9}{{16}}}+2} \right)[/latex]

Step 5: Before we factorise the perfect square we have created, we need to take the [latex]\scriptsize -\displaystyle \frac{9}{{16}}[/latex] and [latex]\scriptsize 2[/latex] terms out of the brackets. But when we do so, we need to remember to multiply them by [latex]\scriptsize 2[/latex].
[latex]\scriptsize \begin{align*}2\left( {{{x}^{2}}-\displaystyle \frac{3}{2}x{\color{Red} +\displaystyle \frac{9}{{16}}-\displaystyle \frac{9}{{16}}}+2} \right)&=2\left( {{{x}^{2}}-\displaystyle \frac{3}{2}x{\color{Red} +\displaystyle \frac{9}{{16}}}} \right){\color{Red} -\displaystyle \frac{9}{8}}+4\end{align*}[/latex]

Step 6: Factorise the newly created perfect square quadratic expression.
[latex]\scriptsize \begin{align*}2{\color{Green}{\left(x^2-\displaystyle \frac{3}{2}x+\displaystyle \frac{9}{16} \right)}}-{\color{Red}{\displaystyle \frac{9}{8}}}+4&=2{\color{Green}{\left(x-\displaystyle \frac{3}{4} \right) \left(x-\displaystyle \frac{3}{4}\right)}}-{\color{Red}{\displaystyle \frac{9}{8}}}+4&& \text{Note how the perfect square quadratic factorises}\\ &=2{\color{Green}{\left(x-\displaystyle \frac{3}{4}\right)^2}}-{\color{Red}{\displaystyle \frac{9}{8}}}+4\end{align*}[/latex]

Step 7: Collect the constants.
[latex]\scriptsize \begin{align*}2{\color{Green} {{\left( {x-\displaystyle \frac{3}{4}} \right)}^{2}}}{\color{Red} -\displaystyle \frac{9}{8}}+4&=2{\color{Green} {{\left( {x-\displaystyle \frac{3}{2}} \right)}^{2}}}-\displaystyle \frac{{9+32}}{8}\\&=2{\color{Green} {{\left( {x-\displaystyle \frac{3}{2}} \right)}^{2}}}+\displaystyle \frac{{23}}{8}\end{align*}[/latex]

Exercise 3.1

Complete the square for the following expressions:

1. [latex]\scriptsize {{x}^{2}}+6x[/latex]
2. [latex]\scriptsize {{x}^{2}}+\displaystyle \frac{5}{7}x[/latex]
3. [latex]\scriptsize {{x}^{2}}-\displaystyle \frac{5}{7}x-1[/latex]
4. [latex]\scriptsize {{x}^{2}}-2x+6[/latex]
5. [latex]\scriptsize 5{{x}^{2}}+10x+15[/latex]
6. [latex]\scriptsize 9+6x-3{{x}^{2}}[/latex]

The full solutions are at the end of the unit.

Note

For a generalised summary of the process of completing the square of any quadratic expression, watch this animation.

 

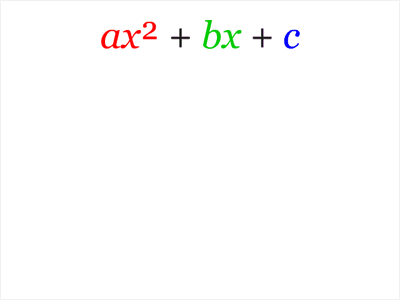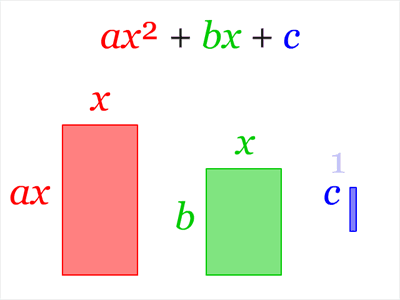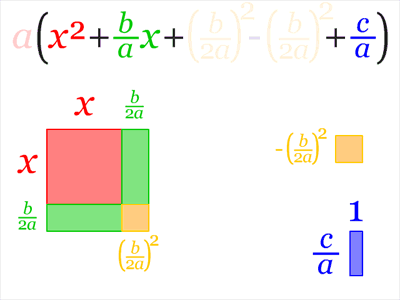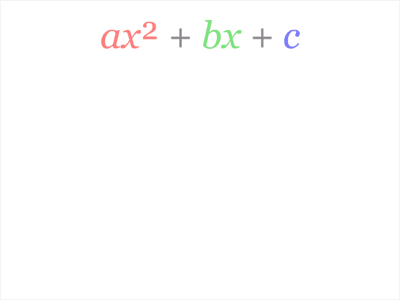
Summary

In this unit you have learnt the following:

• How to complete the square of any quadratic expression [latex]\scriptsize a{{x}^{2}}+bx+c[/latex].

Unit 3: Assessment

Suggested time to complete: 25 minutes

Complete the square for the following expressions:

1. [latex]\scriptsize {{x}^{2}}+5x-6[/latex]
2. [latex]\scriptsize {{x}^{2}}-4x-8[/latex]
3. [latex]\scriptsize {{x}^{2}}+6x-4[/latex]
4. [latex]\scriptsize 10{{x}^{2}}-7x-12[/latex]
5. [latex]\scriptsize 2-12x-3{{x}^{2}}[/latex]
6. [latex]\scriptsize a{{x}^{2}}+bx+c[/latex]

The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

1. .
   [latex]\scriptsize \begin{align*}&{{x}^{2}}+6x && \left [\left ( \displaystyle \frac{b}{2} \right )^2=9 \right ]\\&={{x}^{2}}+6x+9-9\\&={{(x+3)}^{2}}-9\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}&{{x}^{2}}+\displaystyle \frac{5}{7}x && \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}={{{\left( {\displaystyle \frac{5}{{14}}} \right)}}^{2}}=\displaystyle \frac{{25}}{{196}}} \right]\\&={{x}^{2}}+\displaystyle \frac{5}{7}x+\displaystyle \frac{{25}}{{196}}-\displaystyle \frac{{25}}{{196}}\\&={{\left( {x+\displaystyle \frac{5}{{14}}} \right)}^{2}}-\displaystyle \frac{{25}}{{196}}\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}&{{x}^{2}}-\displaystyle \frac{5}{7}x-1 && \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}={{{\left( {-\displaystyle \frac{5}{{14}}} \right)}}^{2}}=\displaystyle \frac{{25}}{{196}}} \right]\\&={{x}^{2}}-\displaystyle \frac{5}{7}x+\displaystyle \frac{{25}}{{196}}-\displaystyle \frac{{25}}{{196}}-1\\&={{\left( {x-\displaystyle \frac{5}{{14}}} \right)}^{2}}-\displaystyle \frac{{25-196}}{{196}}\\&={{\left( {x-\displaystyle \frac{5}{{14}}} \right)}^{2}}-\displaystyle \frac{{221}}{{196}}\end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*}&{{x}^{2}}-2x+6 && \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}={{{(-1)}}^{2}}=1} \right]\\&={{x}^{2}}-2x+1-1+6\\&={{(x-1)}^{2}}+5\end{align*}[/latex]
5. .
   [latex]\scriptsize \begin{align*}&5{{x}^{2}}+10x+15\\&=5({{x}^{2}}+2x+3)&& \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}=1} \right]\\&=5({{x}^{2}}+2x+1-1+3)\\&=5({{x}^{2}}+2x+1)-5+15&&\text{Remember to multiply the constants by the}\\&&&\text{common factor when you take them out of the bracket}\\&=5{{(x+1)}^{2}}+10\end{align*}[/latex]
6. .
   [latex]\scriptsize \begin{align*}&9+6x-3{{x}^{2}}\\&=-3(-3-2x+{{x}^{2}})\\&=-3({{x}^{2}}-2x-3)\quad \quad \quad \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}=1} \right]\\&=-3({{x}^{2}}-2x+1-1-3)\\&=-3({{x}^{2}}-2x+1)+3+9\quad \text{Remember to multiply the constants by }-3\\&=-3{{(x-1)}^{2}}+12\end{align*}[/latex]

Back to Exercise 3.1

Unit 3: Assessment

1. .
   [latex]\scriptsize \begin{align*}&{{x}^{2}}+5x-6\quad \quad \quad \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}={{{\left( {\displaystyle \frac{5}{2}} \right)}}^{2}}=\displaystyle \frac{{25}}{4}} \right]\\&={{x}^{2}}+5x+\displaystyle \frac{{25}}{4}-\displaystyle \frac{{25}}{4}-6\\&={{\left( {x+\displaystyle \frac{5}{2}} \right)}^{2}}-\displaystyle \frac{{25-24}}{4}\\&={{\left( {x+\displaystyle \frac{5}{2}} \right)}^{2}}-\displaystyle \frac{{49}}{4}\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}&{{x}^{2}}-4x-8\quad \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}={{{(-2)}}^{2}}=4} \right]\\&={{x}^{2}}-4x+4-4-8\\&={{(x-2)}^{2}}-12\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}&{{x}^{2}}+6x-4\quad \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}=9} \right]\\&={{x}^{2}}+6x+9-9-4\\&={{(x+3)}^{2}}-13\end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*}&10{{x}^{2}}-7x-12\\&=10\left( {{{x}^{2}}-\displaystyle \frac{7}{{10}}x} \right)-12\quad \quad \quad \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}={{{\left( {\displaystyle \frac{7}{{20}}} \right)}}^{2}}=\displaystyle \frac{{49}}{{400}}} \right]\\ &\text{Instead of taking the common factor from }-12\text{ we can leave it outside the bracket}\\ &=10 \left( {x-\displaystyle \frac{7}{{10}}x+\displaystyle \frac{{49}}{{400}}-\displaystyle \frac{{49}}{{400}}} \right)-12\\&=10\left( {x-\displaystyle \frac{7}{{10}}x+\displaystyle \frac{{49}}{{400}}} \right)-\left( {\displaystyle \frac{{49}}{{40\bcancel{0}}}\times \displaystyle \frac{{\bcancel{{10}}}}{1}} \right)-12\\&=10\left( {x-\displaystyle \frac{7}{{10}}x+\displaystyle \frac{{49}}{{400}}} \right)-\displaystyle \frac{{49}}{{10}}-12\\&=10{{\left( {x-\displaystyle \frac{7}{{20}}} \right)}^{2}}-\displaystyle \frac{{49-480}}{{40}}\\&=10{{\left( {x-\displaystyle \frac{7}{{20}}} \right)}^{2}}-\displaystyle \frac{{529}}{{40}}\end{align*}[/latex]
5. .
   [latex]\scriptsize \begin{align*}&2-12x-3{{x}^{2}}\quad \text{Take out a common factor of }-3\\&=2-3(4x+{{x}^{2}})\\&=-3({{x}^{2}}+4x)+2\quad \quad \quad \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}=4} \right]\\&=-3({{x}^{2}}+4x+4-4)+2\\&=-3({{x}^{2}}+4x+4)+12+2\\&=-3{{(x+2)}^{2}}+14\end{align*}[/latex]
6. .
   [latex]\scriptsize \begin{align*}&a{{x}^{2}}+bx+c\\&=a\left( {{{x}^{2}}+\displaystyle \frac{b}{a}x} \right)+c\quad \left[ {{{{\left( {\displaystyle \frac{b}{2}} \right)}}^{2}}={{{\left( {\displaystyle \frac{b}{{2a}}} \right)}}^{2}}=\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}} \right]\\&=a\left( {{{x}^{2}}+\displaystyle \frac{b}{a}x+\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}-\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}} \right)+c\\&=a\left( {{{x}^{2}}+\displaystyle \frac{b}{a}x+\displaystyle \frac{{{{b}^{2}}}}{{4{{a}^{2}}}}} \right)-\displaystyle \frac{{{{b}^{2}}}}{{4a}}+c\\&=a{{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}}+c-\displaystyle \frac{{{{b}^{2}}}}{{4a}}\\&=a{{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}}+\displaystyle \frac{{4ac-{{b}^{2}}}}{{4a}}\\&=a{{\left( {x+\displaystyle \frac{b}{{2a}}} \right)}^{2}}+\left( {\displaystyle \frac{{-{{b}^{2}}+4ac}}{{4a}}} \right)\end{align*}[/latex]

Back to Unit 3: Assessment