Unit outcomes

By the end of this unit you will be able to:

• Use the Cartesian co-ordinate system to derive the equation of a line through two given points using:
  • the two-point form
  • the gradient-point form
  • the gradient-intercept form.

What you should know

Before you start this unit, make sure you can:

• Plot points on the Cartesian plane. Refer to level 2 subject outcome 3.3 unit 1 if you need help with this.
• Calculate the distance, gradient and midpoint between two points on the Cartesian plane. Refer to level 2 subject outcome 3.3 unit 2 if you need help with this.
• Solve a system of two linear equations simultaneously. Refer to level 2 subject outcome 2.3 unit 4 if you need help with this.

Here is a short self-assessment to make sure you have the skills you need to proceed with this unit.

1. Plot the following points on a Cartesian plane:
   1. [latex]\scriptsize A(-7,-4)[/latex]
   2. [latex]\scriptsize B(5,2)[/latex]
   3. [latex]\scriptsize C(-6,5)[/latex]
2. Calculate the distance [latex]\scriptsize AB[/latex].
3. Calculate the midpoint of [latex]\scriptsize BC[/latex].
4. Calculate the gradient of [latex]\scriptsize AC[/latex].

Solutions

1. .
   
2. .
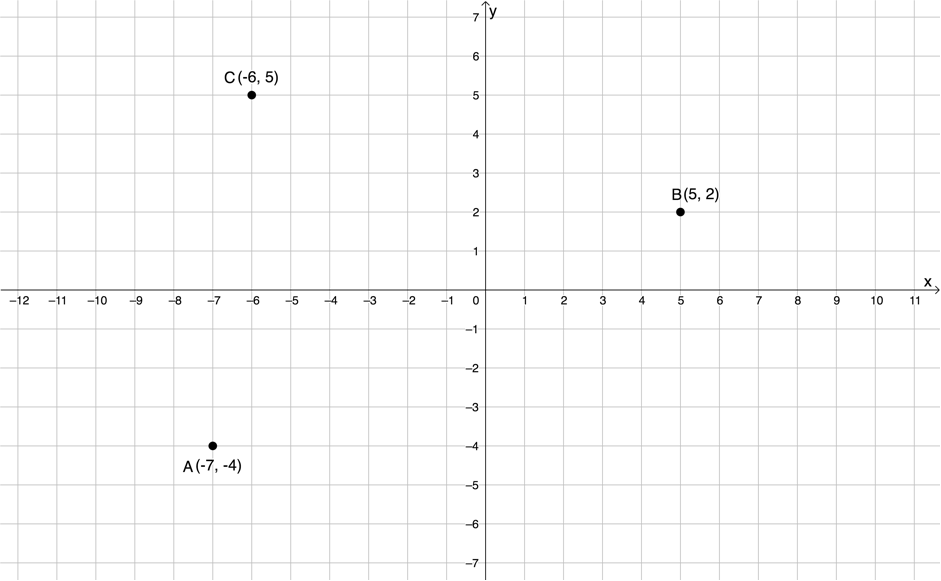
   [latex]\scriptsize \begin{align*}AB&=\sqrt{{{{{\left( {{{x}_{2}}-{{x}_{1}}} \right)}}^{2}}+{{{\left( {{{y}_{2}}-{{y}_{1}}} \right)}}^{2}}}}\\&=\sqrt{{{{{\left( {5-(-7)} \right)}}^{2}}+{{{\left( {2-(-4)} \right)}}^{2}}}}\\&=\sqrt{{{{{12}}^{2}}+{{6}^{2}}}}\\&=\sqrt{{144+36}}\\&=\sqrt{{180}}\\&=\sqrt{{36\times 5}}\\&=6\sqrt{5}\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}{{M}_{{BC}}}&=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\\&=\left( {\displaystyle \frac{{5-6}}{2},\displaystyle \frac{{2+5}}{2}} \right)\\&=\left( {-\displaystyle \frac{1}{2},3\displaystyle \frac{1}{2}} \right)\end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*}{{m}_{{AC}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{5-(-4)}}{{-6-(-7)}}\\&=\displaystyle \frac{9}{1}\\&=9\end{align*}[/latex]

Introduction

In level 2 subject outcome 3.3 we started to learn about an area of mathematics called analytical geometry. Analytical geometry is the study of geometric objects and shapes (points, lines quadrilaterals, etc.) on the Cartesian plane. In that subject outcome we learnt some of the basics involved, such as how to plot points in the Cartesian plane, how to find the distance between any two points, how to find the midpoint between any two points and how to find the gradient of the line between any two points.

Take note!

The distance formula (to calculate the distance between any two points [latex]\scriptsize A({{x}_{1}},{{y}_{1}})[/latex] and [latex]\scriptsize B({{x}_{2}},{{y}_{2}})[/latex]) is:
[latex]\scriptsize AB=\sqrt{{{{{\left( {{{x}_{2}}-{{x}_{1}}} \right)}}^{2}}+{{{\left( {{{y}_{2}}-{{y}_{1}}} \right)}}^{2}}}}[/latex]

Take note!

The midpoint formula (to calculate the midpoint between any two points [latex]\scriptsize A({{x}_{1}},{{y}_{1}})[/latex] and [latex]\scriptsize B({{x}_{2}},{{y}_{2}})[/latex]) is:
[latex]\scriptsize {{M}_{{AB}}}=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)[/latex]

Take note!

The gradient formula (to calculate the gradient between any two points [latex]\scriptsize A({{x}_{1}},{{y}_{1}})[/latex] and [latex]\scriptsize B({{x}_{2}},{{y}_{2}})[/latex]) is:
[latex]\scriptsize {{m}_{{AB}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex]

A great deal of analytical geometry relies on us being able to find the equations of straight lines and line segments between different points. Therefore, in this unit, we are going to learn about three different methods to find the equation of any straight line or line segment on the Cartesian plane.

Take note!

A straight line is infinite and has no beginning or end. A line segment is a finite portion of a straight line between two specific points.

The first of these methods is useful when we know any two points that lie on the straight line.

Find the equation of a straight line using the two-point method

We already know that the gradient between any two points [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex] on the Cartesian plane is given by [latex]\scriptsize {{m}_{{AB}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex].

Figure 1 shows a situation where we know the coordinates of two points on a straight line. These are the points [latex]\scriptsize A(2,5)[/latex] and [latex]\scriptsize B(-2,-3)[/latex].

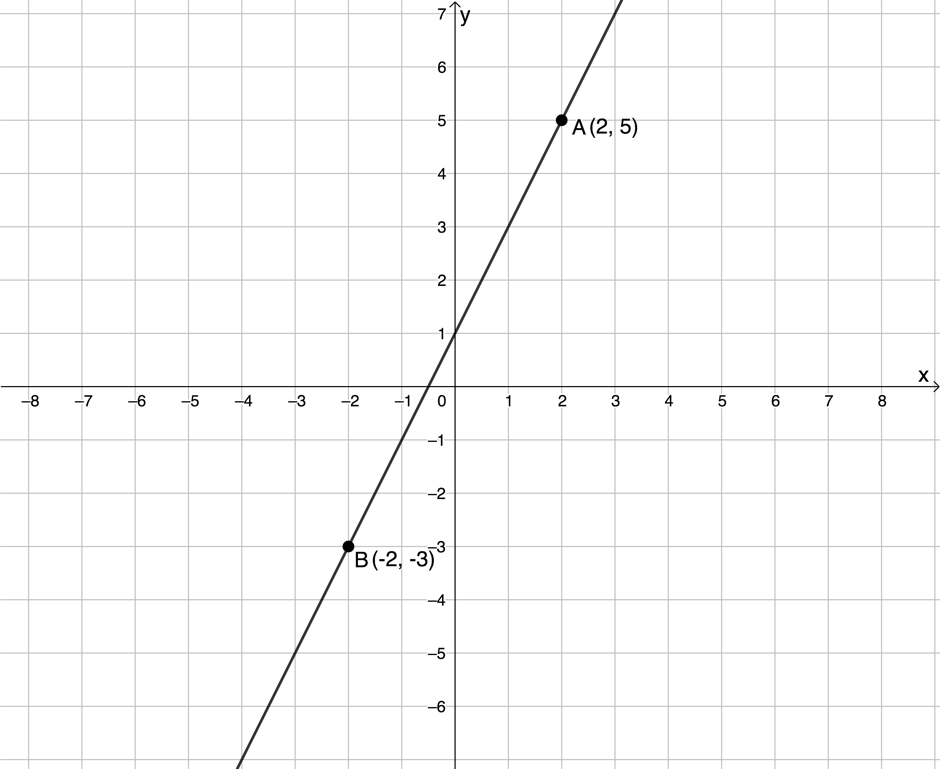
However, we need to find the equation that describes the relationship between the x- and y-coordinates of every point on that line.

Suppose we choose any random point on this straight line, say [latex]\scriptsize C(x,y)[/latex]. We know that the gradient between this point and either of the other two points will be the same as the gradient between points [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex]. All the points lie on the same straight line and the gradient is constant (see Figure 2).

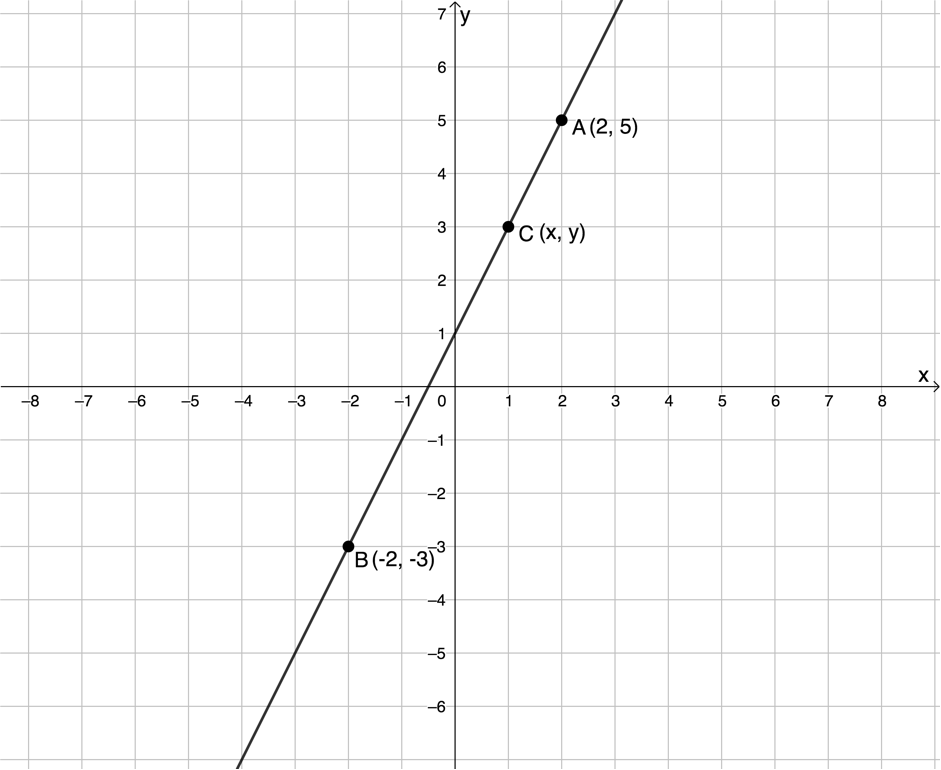
Therefore, we can say that [latex]\scriptsize {{m}_{{AB}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex] is equal to [latex]\scriptsize {{m}_{{AC}}}=\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}}[/latex].
In other words,[latex]\scriptsize \displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex].

If we substitute in the values we have, and rearrange the equation into the familiar [latex]\scriptsize y=mx+c[/latex] form of the straight line we get:
[latex]\scriptsize \begin{align*}\displaystyle \frac{{y-5}}{{x-2}} & =\displaystyle \frac{{-3-5}}{{-2-2}}\\\therefore \displaystyle \frac{{y-5}}{{x-2}} & =\displaystyle \frac{8}{4}\\\therefore y-5 & =2(x-2)\\\therefore y-5 & =2x-4\\\therefore y & =2x+1\end{align*}[/latex]

This is the equation of the straight line that passes through points [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex]. Have a closer look at figure 2 to satisfy yourself that the gradient of this line is [latex]\scriptsize 2[/latex] and that the y-intercept is [latex]\scriptsize 1[/latex].

So, when we are given any two points on a straight line we can find the equation of that line by using the two-point form of the straight line equation.

Example 1.1

Find the equation of the straight line passing through [latex]\scriptsize R(3,-4)[/latex] and [latex]\scriptsize S(-5,4)[/latex].

Solution

Because we have been given two points on the straight line, we can use the two-point form of the straight line equation.

Let [latex]\scriptsize R(3,-4)[/latex] be [latex]\scriptsize ({{x}_{1}},{{y}_{1}})[/latex]. Let [latex]\scriptsize S(-5,4)[/latex] be [latex]\scriptsize ({{x}_{2}},{{y}_{2}})[/latex].

[latex]\scriptsize \begin{align*}\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\\therefore \displaystyle \frac{{y-(-4)}}{{x-3}} & =\displaystyle \frac{{4-(-4)}}{{-5-3}}\\\therefore \displaystyle \frac{{y+4}}{{x-3}} & =-\displaystyle \frac{8}{8}=-1\\\therefore y+4 & =-(x-3)\\\therefore y+4 & =-x+3\\\therefore y & =-x-1\end{align*}[/latex]

It is always a good idea to make a quick sketch of the points and join them with a straight line to make sure that you are correct. Here we can see that the gradient is indeed [latex]\scriptsize -1[/latex] and the y-intercept is at [latex]\scriptsize -1[/latex].

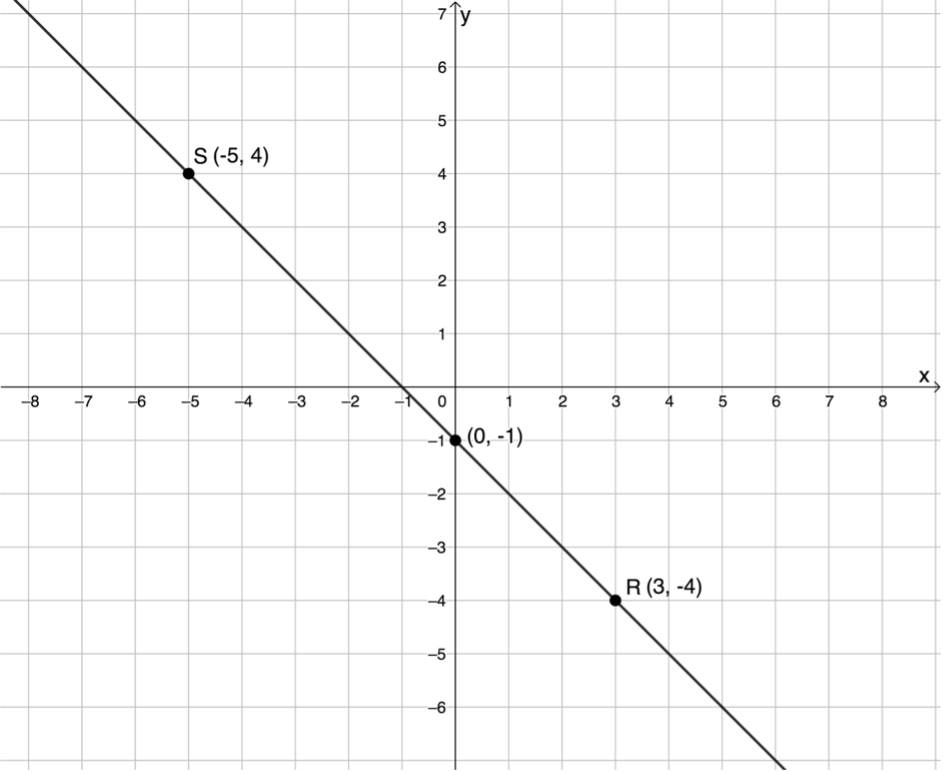
Exercise 1.1

Determine the equations of the straight lines passing through the following points:

1. [latex]\scriptsize (3,7)[/latex] and [latex]\scriptsize (-6,1)[/latex]
2. [latex]\scriptsize (3,5)[/latex] and [latex]\scriptsize (2,3)[/latex]
3. [latex]\scriptsize (-7,-5)[/latex] and [latex]\scriptsize (1,-5)[/latex]
4. [latex]\scriptsize (a,b)[/latex] and [latex]\scriptsize (b,a)[/latex]
5. [latex]\scriptsize (0,r)[/latex] and [latex]\scriptsize (2s,-r)[/latex]

The full solutions are at the end of the unit.

Find the equation of a straight line using the gradient-point method

From the previous section, we know that we can find the equation of a straight line between any two points by using the two-point form of the equation of a straight line.

[latex]\scriptsize \displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex]

But what if, we are given the gradient of the line and any one point on the line? If we know the gradient, we can replace [latex]\scriptsize \displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex] in the two-point form with the value of [latex]\scriptsize m[/latex]. The equation then becomes [latex]\scriptsize \displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}}=m[/latex] which we can simplify to [latex]\scriptsize y-{{y}_{1}}=m(x-{{x}_{1}})[/latex]. This is the gradient-point form of the straight-line equation.

Example 1.2

Determine the equation of the straight line with a gradient of [latex]\scriptsize \displaystyle \frac{3}{2}[/latex] passing through the point [latex]\scriptsize (2,-7)[/latex].

Solution

Because we have been given the gradient and one point on the straight line, we can use the gradient-point form of the straight line equation.

[latex]\scriptsize m=\displaystyle \frac{3}{2}[/latex] and [latex]\scriptsize ({{x}_{1}},{{y}_{1}})[/latex] is [latex]\scriptsize (2,-7)[/latex]

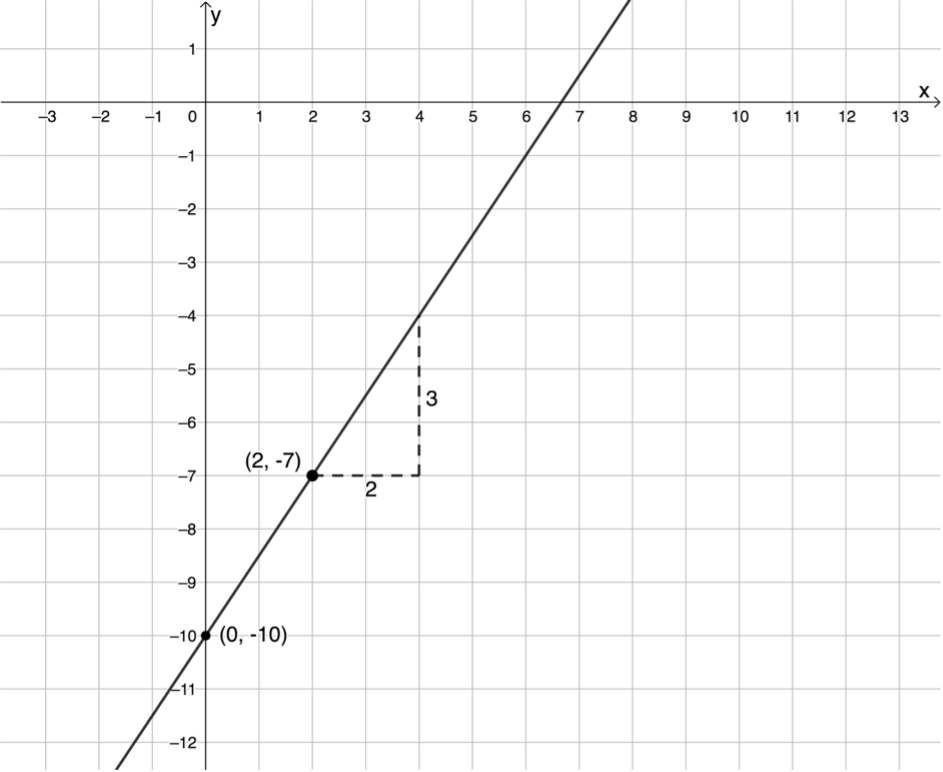
[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-7) & =\displaystyle \frac{3}{2}(x-2)\\\therefore y+7 & =\displaystyle \frac{3}{2}x-3\\\therefore y & =\displaystyle \frac{3}{2}x-10\end{align*}[/latex]

It is a good idea to make a sketch of the straight line to confirm that your equation is correct.

Exercise 1.2

Determine the equations of the following straight lines:

1. passing through the point [latex]\scriptsize (-3,4)[/latex] with a gradient of [latex]\scriptsize -2[/latex]
2. with a gradient of [latex]\scriptsize 0.75[/latex] and passing through [latex]\scriptsize (2,-3)[/latex]
3. where [latex]\scriptsize m=-\displaystyle \frac{4}{5}[/latex] passing through [latex]\scriptsize \left( {\displaystyle \frac{3}{4},\displaystyle \frac{1}{4}} \right)[/latex]
4. with a zero gradient and passing through [latex]\scriptsize (a,b)[/latex]
5. with an undefined gradient and passing through [latex]\scriptsize (-4,y)[/latex]
6. passing through the point [latex]\scriptsize (-2,-6a+b)[/latex] with a gradient of [latex]\scriptsize m=-2a[/latex]

The full solutions are at the end of the unit.

Find the equation of a straight line using the gradient-intercept form of the straight line equation

Obviously, we can always use the standard form of the straight-line equation – [latex]\scriptsize y=mx+c[/latex] (or [latex]\scriptsize y=ax+q[/latex]). This is the one that is probably most familiar to you. If you are ever given the gradient and the y-intercept, it is simply a matter to substitute these values into the equation.

However, questions will seldom be this straightforward!

Example 1.3

Determine the equation of the straight line passing through [latex]\scriptsize (-1,2)[/latex] with a gradient [latex]\scriptsize m=\displaystyle \frac{2}{3}[/latex] using the gradient-intercept form of the straight line equation.

Solution

The gradient intercept form is [latex]\scriptsize y=mx+c[/latex]. We know that [latex]\scriptsize m=\displaystyle \frac{2}{3}[/latex]. Therefore, [latex]\scriptsize y=\displaystyle \frac{2}{3}x+c[/latex].

We have also been given the point [latex]\scriptsize (-1,2)[/latex] that lies on the line, so we can substitute these values in for [latex]\scriptsize x[/latex] and [latex]\scriptsize y[/latex] and solve the equation for [latex]\scriptsize c[/latex].
[latex]\scriptsize \begin{align*}y & =\displaystyle \frac{2}{3}x+c\\\therefore 2 & =\displaystyle \frac{2}{3}(-1)+c\\\therefore 2+\displaystyle \frac{2}{3} & =c\\\therefore c & =\displaystyle \frac{8}{3}\end{align*}[/latex]
Therefore, the equation of the straight line is [latex]\scriptsize y=\displaystyle \frac{2}{3}x+\displaystyle \frac{8}{3}[/latex].

Example 1.4

Determine the equation of the straight line that passes through [latex]\scriptsize (-2,1)[/latex] and [latex]\scriptsize (7,-6)[/latex] by using the standard form of the straight line equation.

Solution

We have been asked to find the equation of the straight line using the gradient-intercept (or standard) form of the equation. To do so, we use each point to set up an equation in standard form and then solve for [latex]\scriptsize m[/latex] and [latex]\scriptsize c[/latex] simultaneously.

Using [latex]\scriptsize (-2,1)[/latex]:
[latex]\scriptsize \begin{align*}1&=m(-2)+c\\\therefore 1&=-2m+c\quad (1)\end{align*}[/latex]

Using [latex]\scriptsize (7,-6)[/latex]:
[latex]\scriptsize \begin{align*}-6&=m(7)+c\\\therefore -6&=7m+c\quad (2)\end{align*}[/latex]

From (1): [latex]\scriptsize c=1+2m[/latex] (3)

Substitute (3) into (2):
[latex]\scriptsize \begin{align*}-6 & =7m+1+2m\\\therefore 9m & =-7\\\therefore m & =-\displaystyle \frac{7}{9}\end{align*}[/latex]

Substitute [latex]\scriptsize m=-\displaystyle \frac{7}{9}[/latex] into (3):
[latex]\scriptsize \begin{align*}c&=1+2\left( {-\displaystyle \frac{7}{9}} \right)\\&=1-\displaystyle \frac{{14}}{9}\\&=\displaystyle \frac{{9-14}}{9}\\&=-\displaystyle \frac{5}{9}\end{align*}[/latex]

Therefore, the equation of the straight line is [latex]\scriptsize y=-\displaystyle \frac{7}{9}x-\displaystyle \frac{5}{9}[/latex]

Exercise 1.3

Use the gradient-intercept form of the straight line equation to find the equation of the following straight lines:

1. passing through [latex]\scriptsize (1,8)[/latex] and [latex]\scriptsize (\displaystyle \frac{1}{2},4)[/latex]
2. passing through [latex]\scriptsize (4,-2)[/latex] with [latex]\scriptsize m=-2[/latex]
3. [latex]\scriptsize m=\displaystyle \frac{3}{5}[/latex] and cuts the y-axis at [latex]\scriptsize 3[/latex]
4. [latex]\scriptsize m=-\displaystyle \frac{1}{2}[/latex] and cuts the x-axis at [latex]\scriptsize 7[/latex]
5. passing through [latex]\scriptsize (3,-4)[/latex] and the origin

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to find the equation of a straight line using the two-point form of the equation – [latex]\scriptsize \displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex].
• How to find the equation of a straight line using the gradient-point form of the equation – [latex]\scriptsize y-{{y}_{1}}=m(x-{{x}_{1}})[/latex].
• How to find the equation of a straight line using the gradient-intercept form of the equation – [latex]\scriptsize y=mx+c[/latex].

Unit 1: Assessment

Suggested time to complete: 30 minutes

1. Determine the equations of the following straight lines:
   1. passing through [latex]\scriptsize (0,6)[/latex] and [latex]\scriptsize (5,0)[/latex]
   2. parallel to the x-axis and passing through [latex]\scriptsize (-6,-2)[/latex]
   3. a gradient of [latex]\scriptsize m=\displaystyle \frac{5}{2}[/latex] and passing through [latex]\scriptsize (5,2)[/latex]
   4. passing through the points [latex]\scriptsize (2a,b)[/latex] and [latex]\scriptsize (a-b,2b)[/latex]
   5. parallel to the y-axis and passing through the origin
2. Determine the equations of the following straight lines:
   1. .
      
   2. .
      
   3. .
      

The full solutions are at the end of the unit.

Unit 1: Solutions

Exercise 1.1

1. [latex]\scriptsize (3,7)[/latex] and [latex]\scriptsize (-6,1)[/latex]
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\\therefore \displaystyle \frac{{y-7}}{{x-3}} & =\displaystyle \frac{{1-7}}{{-6-3}}\\\therefore \displaystyle \frac{{y-7}}{{x-3}} & =\displaystyle \frac{6}{9}=\displaystyle \frac{2}{3}\\\therefore y-7 & =\displaystyle \frac{2}{3}(x-3)\\\therefore y-7 & =\displaystyle \frac{2}{3}x-2\\\therefore y & =\displaystyle \frac{2}{3}x+5\end{align*}[/latex]
2. [latex]\scriptsize (3,5)[/latex] and [latex]\scriptsize (2,3)[/latex]
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\\therefore \displaystyle \frac{{y-5}}{{x-3}} & =\displaystyle \frac{{3-5}}{{2-3}}\\\therefore \displaystyle \frac{{y-5}}{{x-3}} & =\displaystyle \frac{{-2}}{{-1}}=2\\\therefore y-5 & =2(x-3)\\\therefore y-5 & =2x-6\\\therefore y & =2x-1\end{align*}[/latex]
3. [latex]\scriptsize (-7,-5)[/latex] and [latex]\scriptsize (1,-5)[/latex]
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\\therefore \displaystyle \frac{{y-(-5)}}{{x-(-7)}} & =\displaystyle \frac{{-5-(-5)}}{{1-(-7)}}\\\therefore \displaystyle \frac{{y+5}}{{x+7}} & =\displaystyle \frac{0}{8}=0\\\therefore y+5 & =0(x+7)\\\therefore y & =-5\end{align*}[/latex]
4. [latex]\scriptsize (a,b)[/latex] and [latex]\scriptsize (b,a)[/latex]
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\\therefore \displaystyle \frac{{y-b}}{{x-a}} & =\displaystyle \frac{{a-b}}{{b-a}}\\\therefore \displaystyle \frac{{y-b}}{{x-a}} & =\displaystyle \frac{{a-b}}{{-(-b+a)}}=\displaystyle \frac{{a-b}}{{-(a-b)}}=-1\\\therefore y-b & =-1(x-a)\\\therefore y-b & =-x+a\\\therefore y & =-x+a+b\end{align*}[/latex]
5. [latex]\scriptsize (0,r)[/latex] and [latex]\scriptsize (2s,-r)[/latex]
   [latex]\scriptsize \begin{align*}\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\\therefore \displaystyle \frac{{y-r}}{{x-0}} & =\displaystyle \frac{{-r-r}}{{2s-0}}\\\therefore \displaystyle \frac{{y-r}}{x} & =\displaystyle \frac{{-2r}}{{2s}}=-\displaystyle \frac{r}{s}\\\therefore y-r & =-\displaystyle \frac{r}{s}x\\\therefore y & =-\displaystyle \frac{r}{s}x+r\end{align*}[/latex]

Back to Exercise 1.1

Exercise 1.2

1. .
   [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-4 & =-2\left( {x-(-3)} \right)\\\therefore y-4 & =-2(x+3)\\\therefore y-4 & =-2x-6\\\therefore y & =-2x-2\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-3) & =0.75(x-2)\\\therefore y+3 & =0.75x-1.5\\\therefore y & =0.75x-4.5\\\therefore y & =\displaystyle \frac{3}{4}x-\displaystyle \frac{9}{2}\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-\displaystyle \frac{1}{4} & =-\displaystyle \frac{4}{5}\left( {x-\displaystyle \frac{3}{4}} \right)\\\therefore y-\displaystyle \frac{1}{4} & =-\displaystyle \frac{4}{5}x+\displaystyle \frac{{12}}{{20}}\\\therefore y & =-\displaystyle \frac{4}{5}x+\displaystyle \frac{{12}}{{20}}+\displaystyle \frac{1}{4}\\\therefore y & =-\displaystyle \frac{4}{5}x+\displaystyle \frac{{12}}{{20}}+\displaystyle \frac{5}{{20}}\\\therefore y & =-\displaystyle \frac{4}{5}x+\displaystyle \frac{{17}}{{20}}\end{align*}[/latex]
4. .
   [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-b & =0(x-a)\\\therefore y & =b\end{align*}[/latex]
5. .
   [latex]\scriptsize m[/latex] is undefined. Therefore, the straight line is vertical passing through [latex]\scriptsize (-4,y)[/latex]. Therefore [latex]\scriptsize x=-4[/latex].
6. .
   [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-6a+b) & =-2a\left( {x-(-2)} \right)\\\therefore y+6a-b & =-2a(x+2)\\\therefore y+6a-b & =-2ax-4a\\\therefore y & =-2ax-4a-6a+b\\\therefore y & =-2ax-10a+b\end{align*}[/latex]

Back to Exercise 1.2

Exercise 1.3

1. .
   [latex]\scriptsize (1,8)[/latex]: [latex]\scriptsize 8=m+c[/latex] (1)
   [latex]\scriptsize (\displaystyle \frac{1}{2},4)[/latex]: [latex]\scriptsize 4=\displaystyle \frac{1}{2}m+c[/latex] (2)
   From (1): [latex]\scriptsize c=8-m[/latex] (3)
   Substitute (3) into (2):
   [latex]\scriptsize \begin{align*}4 & =\displaystyle \frac{1}{2}m+8-m\\\therefore \displaystyle \frac{1}{2}m & =4\\\therefore m & =8\end{align*}[/latex]
   Substitute [latex]\scriptsize m=8[/latex] into (3):
   [latex]\scriptsize c=8-8=0[/latex]
   Therefore, the equation of the straight line is [latex]\scriptsize y=8x[/latex].
2. .
   [latex]\scriptsize y=-2x+c[/latex]
   Substitute in [latex]\scriptsize (4,-2)[/latex]:
   [latex]\scriptsize \begin{align*}-2 & =-2(4)+c\\\therefore -2 & =-8+c\\\therefore c & =6\end{align*}[/latex]
   Therefore, the equation of the straight line is [latex]\scriptsize y=-2x+6[/latex].
3. .
   [latex]\scriptsize m=\displaystyle \frac{3}{5}[/latex] and [latex]\scriptsize c=3[/latex]. Therefore, the equation of the straight line is [latex]\scriptsize y=\displaystyle \frac{3}{5}x+3[/latex].
4. .
   [latex]\scriptsize y=-\displaystyle \frac{1}{2}x+c[/latex]
   Substitute in [latex]\scriptsize (7,0)[/latex]:
   [latex]\scriptsize \begin{align*}0 & =-\displaystyle \frac{1}{2}(7)+c\\\therefore c & =\displaystyle \frac{7}{2}\end{align*}[/latex]
   Therefore, the equation of the straight line is [latex]\scriptsize y=-\displaystyle \frac{1}{2}x+\displaystyle \frac{7}{2}[/latex].
5. .
   Passing through [latex]\scriptsize (3,-4)[/latex] and the origin.
   [latex]\scriptsize (3,-4)[/latex]: [latex]\scriptsize -4=3m+c[/latex] (1)
   [latex]\scriptsize (0,0)[/latex]: [latex]\scriptsize 0=c[/latex] (2)
   Substitute (2) into (1):
   [latex]\scriptsize \begin{align*}-4 & =3m+0\\\therefore m & =-\displaystyle \frac{4}{3}\end{align*}[/latex]
   Therefore, the equation of the straight line is [latex]\scriptsize y=-\displaystyle \frac{4}{3}x[/latex].

Back to Exercise 1.3

Unit 1: Assessment

1. .
   1. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\\therefore \displaystyle \frac{{y-6}}{{x-0}} & =\displaystyle \frac{{0-6}}{{5-0}}\\\therefore \displaystyle \frac{{y-6}}{x} & =-\displaystyle \frac{6}{5}\\\therefore y-6 & =-\displaystyle \frac{6}{5}x\\\therefore y & =-\displaystyle \frac{6}{5}x+6\end{align*}[/latex]
   2. Parallel to the x-axis means that [latex]\scriptsize m=0[/latex]. Therefore, the equation of the line is [latex]\scriptsize y=-2[/latex].
   3. .
      [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-2 & =\displaystyle \frac{5}{2}(x-5)\\\therefore y-2 & =\displaystyle \frac{5}{2}x-\displaystyle \frac{{25}}{2}\\\therefore y & =\displaystyle \frac{5}{2}x-\displaystyle \frac{{25}}{2}+2\\\therefore y & =\displaystyle \frac{5}{2}x-\displaystyle \frac{{21}}{2}\end{align*}[/latex]
   4. .
      [latex]\scriptsize \begin{align*} \displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\ \therefore \displaystyle \frac{{y-b}}{{x-2a}}&=\displaystyle \frac{{2b-b}}{{(a-b)-2a}}\\ \therefore \displaystyle \frac{{y-b}}{{x-2a}}&=\displaystyle \frac{b}{{a-b-2a}}=\displaystyle \frac{b}{{-a-b}}=-\displaystyle \frac{b}{{(a+b)}}\\ \therefore y-b&=-\displaystyle \frac{b}{{(a+b)}}(x-2a)\\ \therefore y-b&=-\displaystyle \frac{b}{{(a+b)}}x+\displaystyle \frac{{2ab}}{{(a+b)}}\\ \therefore y&=-\displaystyle \frac{b}{{(a+b)}}x+\displaystyle \frac{{2ab}}{{(a+b)}}+b\\ \therefore y&=-\displaystyle \frac{b}{{(a+b)}}x+\displaystyle \frac{{b(2ab)+b(a+b)}}{{(a+b)}}=-\displaystyle \frac{b}{{(a+b)}}x+\displaystyle \frac{{2a{{b}^{2}}+ab+{{b}^{2}}}}{{(a+b)}} \end{align*}[/latex]
   5. Parallel to the y-axis means that the gradient is undefined. Therefore, the equation is [latex]\scriptsize x=0[/latex].
2. .
   1. .
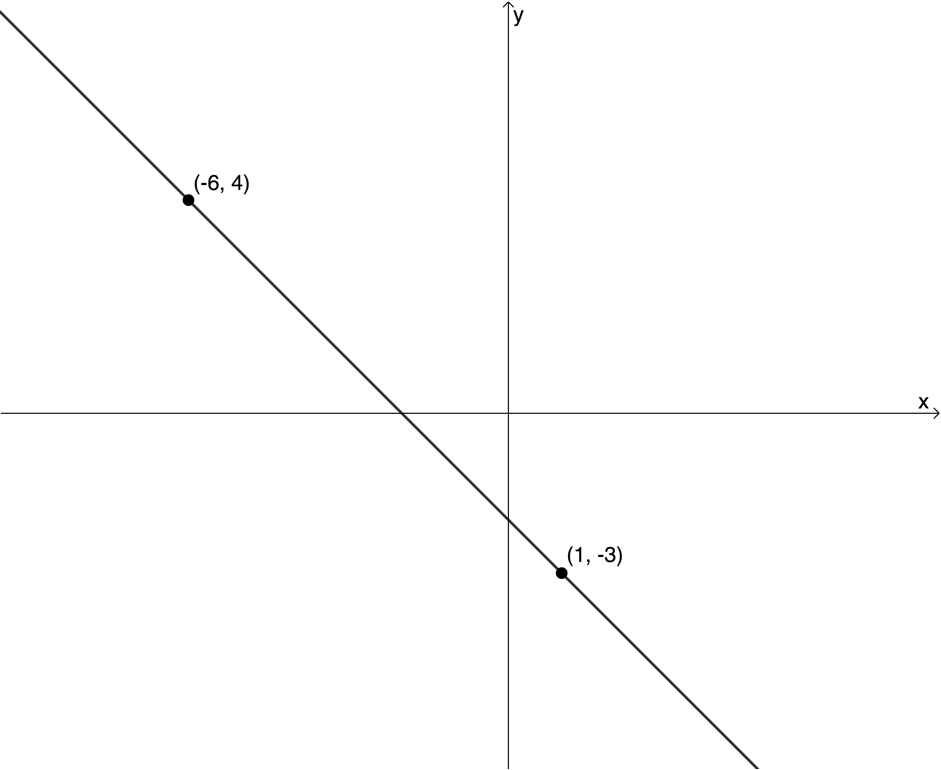
      [latex]\scriptsize \begin{align*} \displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\ \therefore \displaystyle \frac{{y-4}}{{x-(-6)}} & =\displaystyle \frac{{-3-4}}{{1-(-6)}}\\ \therefore \displaystyle \frac{{y-4}}{{x+6}} & =-\displaystyle \frac{7}{7}=-1\\ \therefore y-4 & =-(x+6)\\\therefore y & =-x-2\end{align*}[/latex]
   2. .
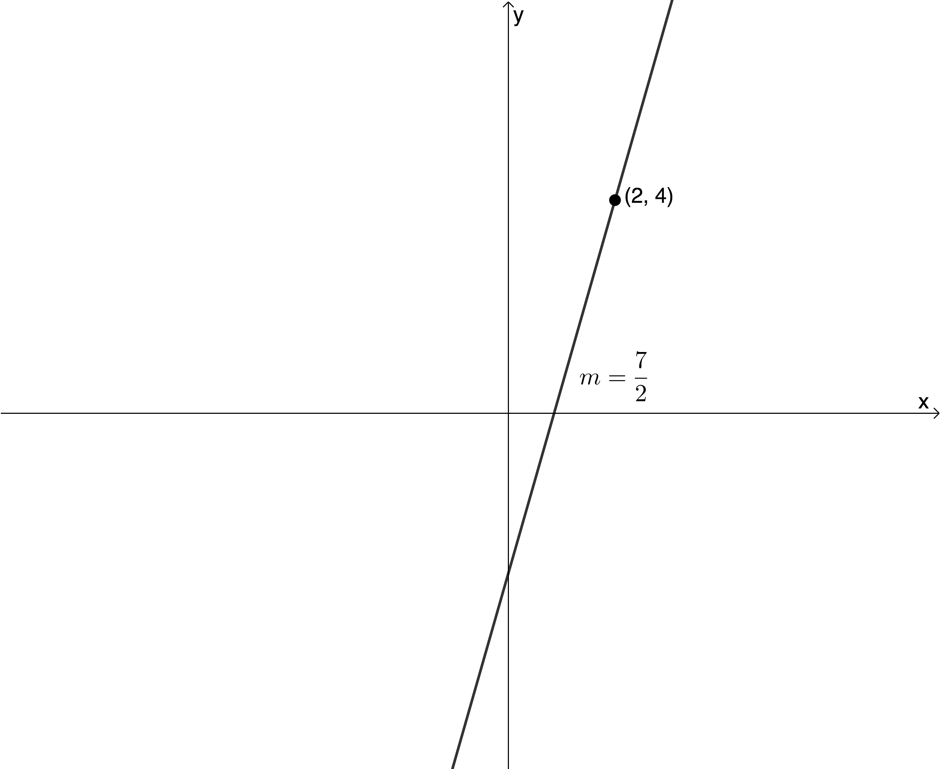
      [latex]\scriptsize \begin{align*} y-{{y}_{1}}&=m(x-{{x}_{1}})\\ \therefore y-4&=\displaystyle \frac{7}{2}(x-2)\\ \therefore y-4&=\displaystyle \frac{7}{2}x-7\\ \therefore y&=\displaystyle \frac{7}{2}x-3 \end{align*}[/latex]
   3. .
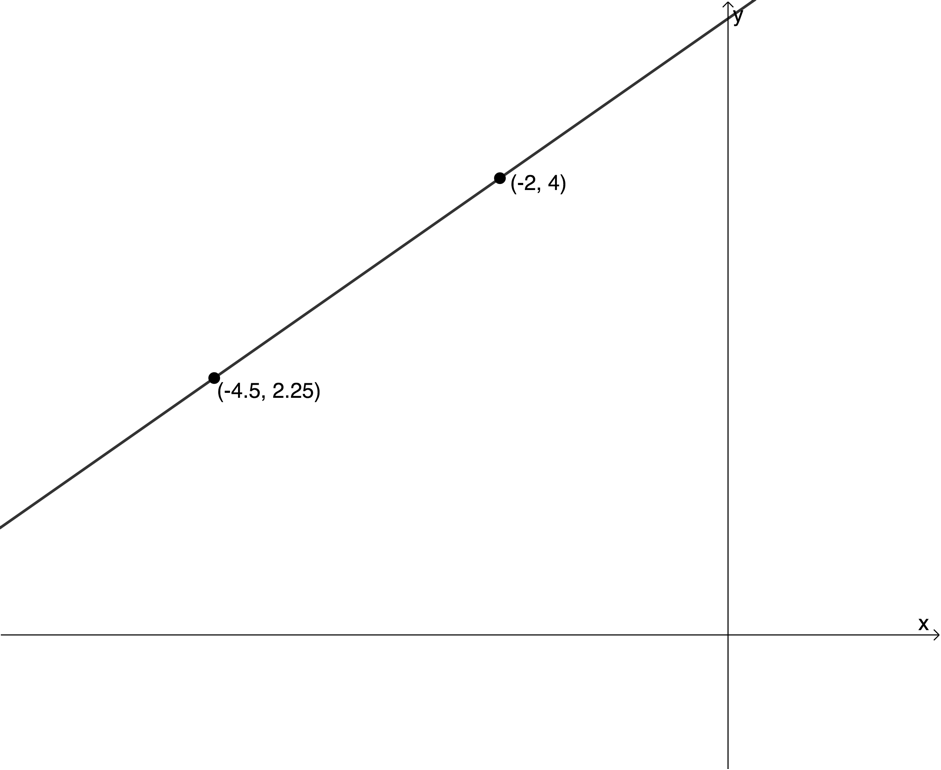
      [latex]\scriptsize \begin{align*} \displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\ \therefore \displaystyle \frac{{y-4}}{{x-(-2)}}&=\displaystyle \frac{{2.25-4}}{{-4.5-(-2)}}\\ \therefore \displaystyle \frac{{y-4}}{{x+2}}&=\displaystyle \frac{{1.75}}{{2.5}}=0.7\\ \therefore y-4&=0.7(x+2)\\ \therefore y&=0.7x+1.4+4\\ \therefore y&=0.7x+5.4 \end{align*}[/latex]

Back to Unit 1: Assessment