Unit outcomes

By the end of this unit you will be able to:

• Determine the equation of a straight line parallel to another straight line on the Cartesian plane.
• Determine the equation of a straight line perpendicular to another straight line on the Cartesian plane.

What you should know

Before you start this unit, make sure you can:

• Determine the equation of a straight line by using any of the following forms of the straight line equation:
  • the standard (or gradient-intercept) form
  • the gradient-point form
  • the two-point form.

Refer to unit 1 in this subject outcome if you need help with this.

Introduction

Sometimes in analytical geometry, we don’t know the gradient of a line and we do not have enough information to find it directly. However, if the line whose equation we are trying to find is parallel or perpendicular to another line, then we can use this information to infer its gradient.

In this unit we will look more closely at what we mean by parallel and perpendicular and how we can infer the gradient of a line based on this.

Parallel lines

Parallel lines in flat 2-D geometry are straight lines that run next to each other but never meet. Parallel lines are like the tracks of a railway line. The distance between them is always the same. They never get nearer or further apart.

Figure 2 shows two parallel lines on the Cartesian plane. Measure the gradient of each line using the two points given. Remember that [latex]\scriptsize m=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex]. What can we say about the gradient of each line?

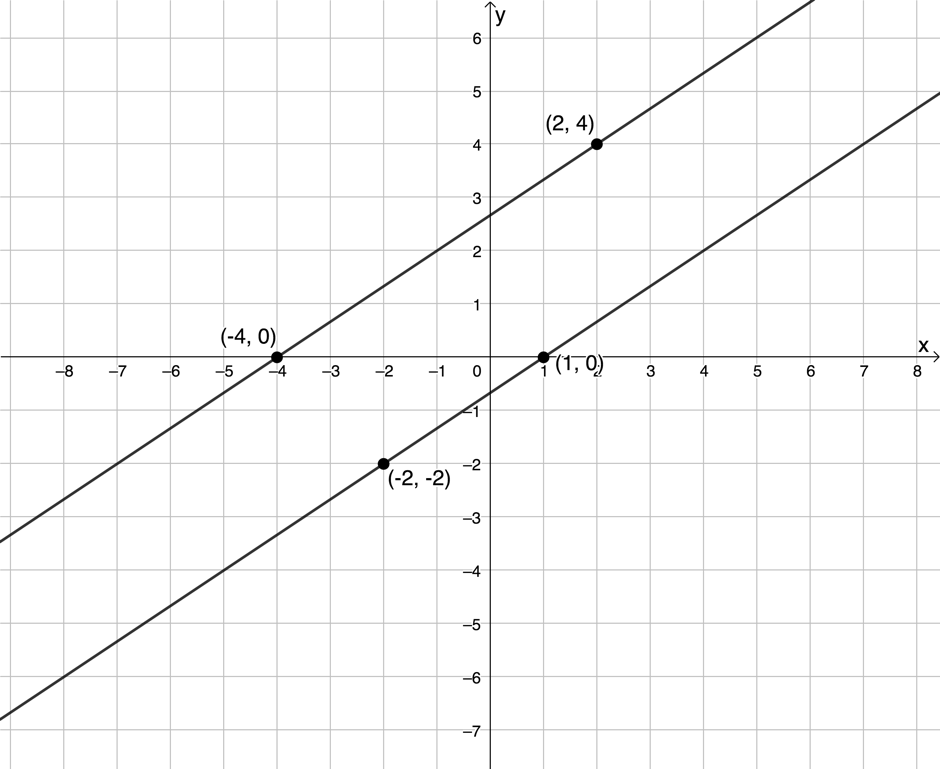
You should have found that the gradient of both lines is [latex]\scriptsize m=\displaystyle \frac{2}{3}[/latex] (see Figure 3). Therefore, we can see that if two straight lines on the Cartesian plane are parallel, then they have the same gradient.

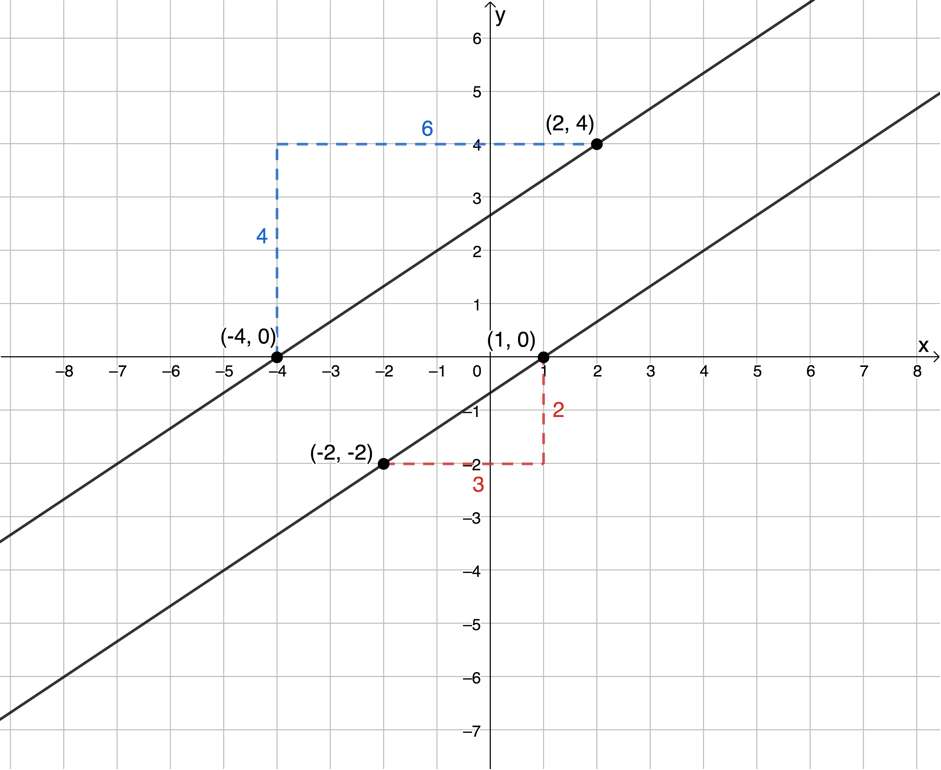
We can use the fact that one line is parallel to another line to help us find its equation because, if the lines are parallel, we can infer the gradient of the line.

Take note!

If two straight lines are parallel, then [latex]\scriptsize {{m}_{1}}={{m}_{2}}[/latex].

Example 2.1

Determine the equation of the line passing through [latex]\scriptsize (-2,5)[/latex] parallel to [latex]\scriptsize 2y-x+4=0[/latex].

Solution

We are told that the line whose equation we want to find is parallel to the line with the equation [latex]\scriptsize 2y-x+4=0[/latex]. We need to rewrite this equation in standard form in order to determine the value of [latex]\scriptsize m[/latex] and hence its gradient.

[latex]\scriptsize \begin{align*}2y-x+4 & =0\\\therefore 2y & =x-4\\\therefore y & =\displaystyle \frac{1}{2}x-2\end{align*}[/latex]
Therefore, [latex]\scriptsize m=\displaystyle \frac{1}{2}[/latex]. So, the line whose equation we want to find also has a gradient of [latex]\scriptsize m=\displaystyle \frac{1}{2}[/latex]. The lines are parallel. We also know a point that this line passes through. Therefore, we can use the gradient-point form of the straight line equation.

[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-5 & =\displaystyle \frac{1}{2}\left( {x-(-2)} \right)\\\therefore y-5 & =\displaystyle \frac{1}{2}(x+2)\\\therefore y-5 & =\displaystyle \frac{1}{2}x+1\\\therefore y & =\displaystyle \frac{1}{2}x+6\end{align*}[/latex]

Here is a sketch of the two lines.

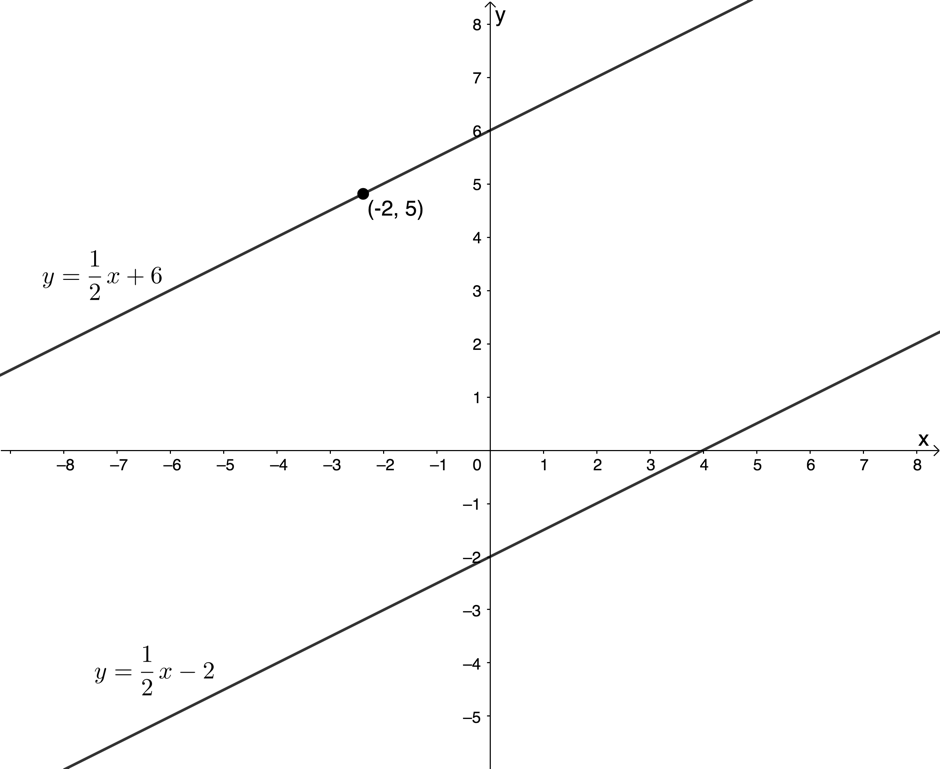
Exercise 2.1

1. Determine the equations of the following straight lines:
   1. passing through [latex]\scriptsize (2,-3)[/latex] and parallel to the line [latex]\scriptsize y+3x-4=0[/latex]
   2. passing through [latex]\scriptsize (-4,1)[/latex] and parallel to the line [latex]\scriptsize 3(y+2x)=7[/latex]
   3. passing through [latex]\scriptsize (-3,-3)[/latex] and parallel to the line passing through [latex]\scriptsize (4,2)[/latex] and [latex]\scriptsize (-2,6)[/latex]
2. Determine whether the following straight lines are parallel or not:
   1. [latex]\scriptsize y+3x=8[/latex] and [latex]\scriptsize 6x=3y-2[/latex]
   2. [latex]\scriptsize \displaystyle \frac{y}{3}+x+5=0[/latex] and [latex]\scriptsize 2y+6x=1[/latex]
   3. [latex]\scriptsize y-1=\displaystyle \frac{1}{3}x[/latex] and the line passing through [latex]\scriptsize (-2,4)[/latex] and [latex]\scriptsize (1,5)[/latex].

The full solutions are at the end of the unit.

Perpendicular lines

In flat 2-D geometry, we say that two lines that meet or intersect at [latex]\scriptsize {{90}^\circ}[/latex] or at right angles are perpendicular to each other (see Figure 4).

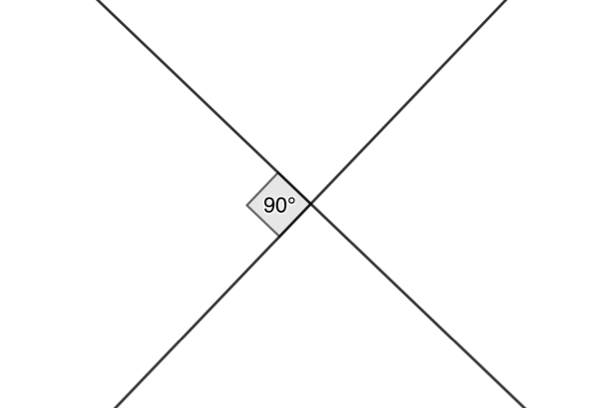
But what can we say about the gradients of these lines?

Activity 2.1: Gradients of perpendicular lines

Time required: 10 minutes

What you need:

• a blank piece of paper or graph paper
• a pen or pencil
• a ruler
• a protractor

What to do:

1. On your blank piece of paper or graph paper, create a Cartesian plane. Now draw any straight line with a gradient of [latex]\scriptsize \displaystyle \frac{3}{2}[/latex] on the Cartesian plane.
2. Use your protractor to measure an angle of [latex]\scriptsize {{90}^\circ}[/latex] to this straight line. Draw another straight line at [latex]\scriptsize {{90}^\circ}[/latex] (or perpendicular) to the first line.
3. Measure the gradient of this second straight line.
4. How are these two gradients related?
5. Write an expression for this relationship.

What did you find?

1. Here is a line with a gradient of [latex]\scriptsize m=\displaystyle \frac{3}{2}[/latex]. The gradient has been measured between points [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex]
   
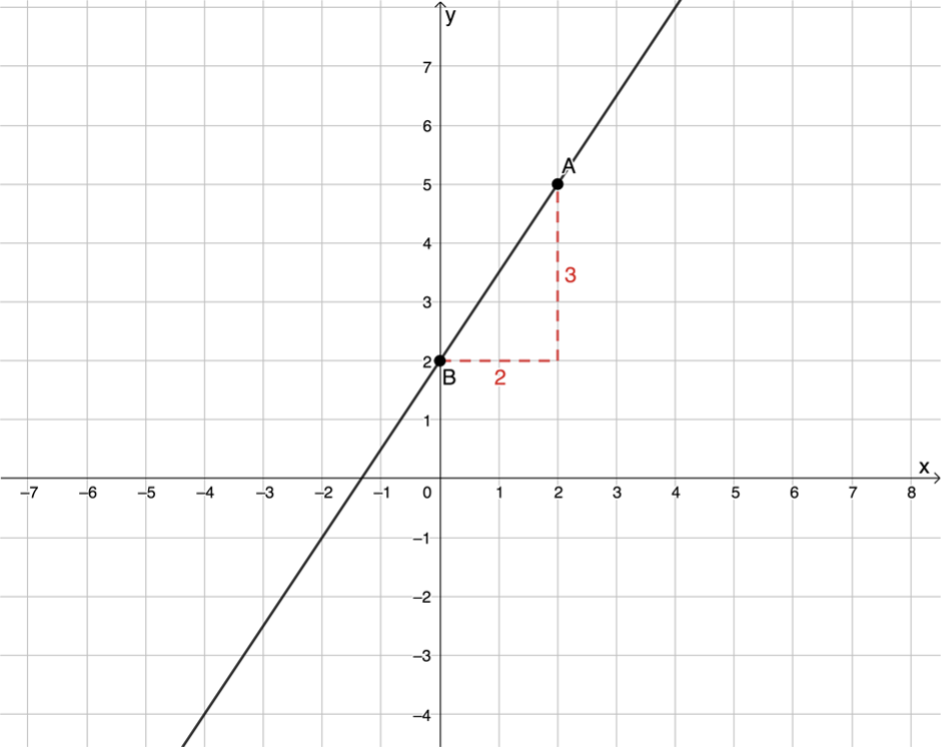
2. Another line (through points [latex]\scriptsize B[/latex] and [latex]\scriptsize C[/latex]) is drawn perpendicular to the first line.
   
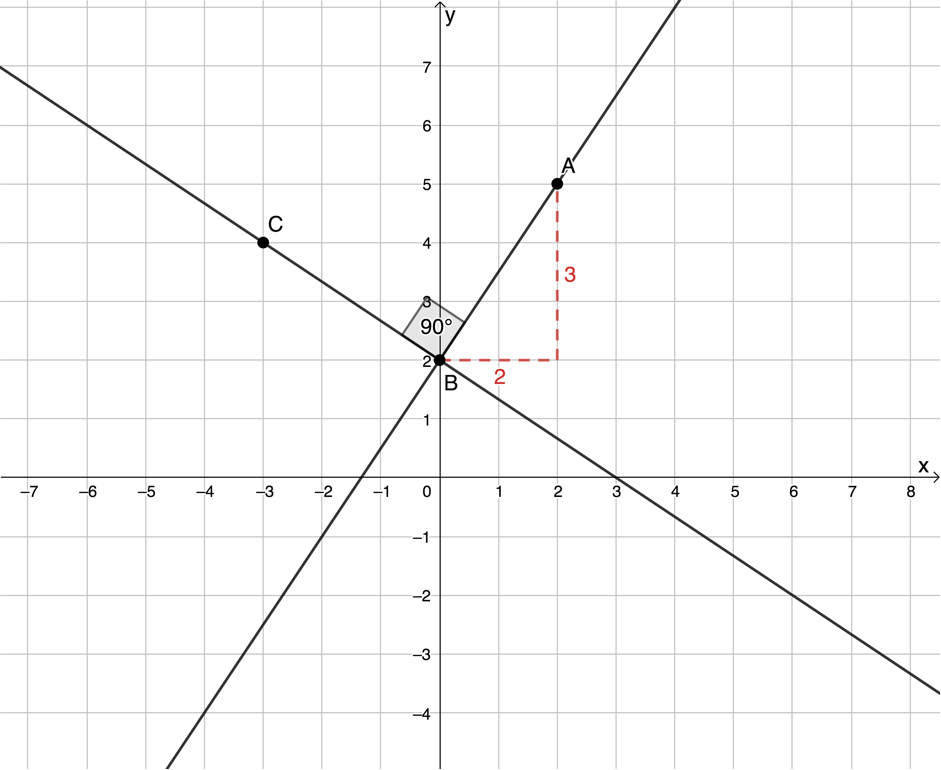
3. The gradient of the second line is measured between points [latex]\scriptsize B[/latex] and [latex]\scriptsize C[/latex]. Notice that the run is [latex]\scriptsize -3[/latex]. Therefore, the gradient is [latex]\scriptsize m=-\displaystyle \frac{2}{3}[/latex].
   
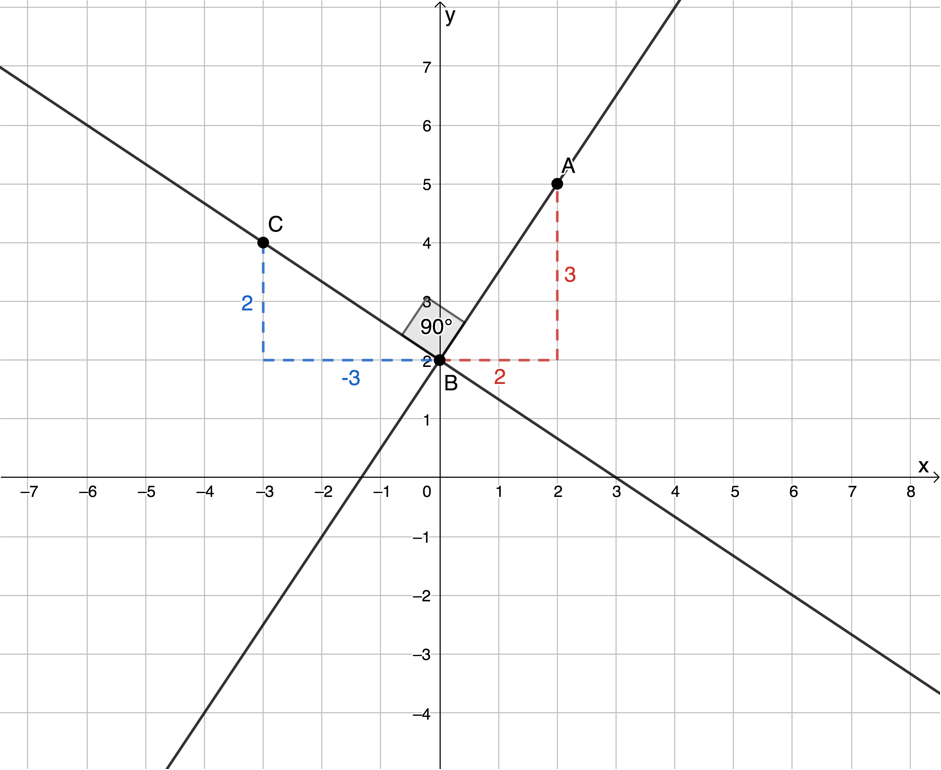
4. The gradients are [latex]\scriptsize {{m}_{1}}=\displaystyle \frac{3}{2}[/latex] and [latex]\scriptsize {{m}_{2}}=-\displaystyle \frac{2}{3}[/latex]. The one gradient is the negative reciprocal or negative multiplicative inverse of the other.
5. [latex]\scriptsize {{m}_{1}}\times {{m}_{2}}=\displaystyle \frac{3}{2}\times -\displaystyle \frac{2}{3}=-1[/latex]

In Activity 2.1, we discovered that the gradients of perpendicular lines are negative reciprocals. Another way of saying this is that, if the lines are perpendicular, then [latex]\scriptsize {{m}_{1}}\times {{m}_{2}}=-1[/latex].

Take note!

If two straight lines are perpendicular, then [latex]\scriptsize {{m}_{1}}\times {{m}_{2}}=-1[/latex].

Example 2.2

Determine the equation of the straight line passing through [latex]\scriptsize (7,4)[/latex] and perpendicular to [latex]\scriptsize \displaystyle \frac{y}{3}-\displaystyle \frac{x}{5}=1[/latex].

Solution

We are told that the line whose equation we want to find is perpendicular to the line with the equation [latex]\scriptsize \displaystyle \frac{y}{3}-\displaystyle \frac{x}{5}=1[/latex]. We need to rewrite this equation in standard form in order to determine the value of [latex]\scriptsize m[/latex] and hence its gradient.

[latex]\scriptsize \begin{align*}\displaystyle \frac{y}{3}-\displaystyle \frac{x}{5} & =1\\\therefore \displaystyle \frac{y}{3} & =\displaystyle \frac{x}{5}+1\\\therefore y & =\displaystyle \frac{{3x}}{5}+3\end{align*}[/latex]
Therefore, [latex]\scriptsize {{m}_{1}}=\displaystyle \frac{3}{5}[/latex]. For perpendicular lines, we know that [latex]\scriptsize {{m}_{1}}\times {{m}_{2}}=-1[/latex]. Therefore, [latex]\scriptsize {{m}_{2}}=-\displaystyle \frac{5}{3}[/latex].

[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-4 & =-\displaystyle \frac{5}{3}(x-7)\\\therefore y-4 & =-\displaystyle \frac{5}{3}x+\displaystyle \frac{{35}}{3}\\\therefore y & =-\displaystyle \frac{5}{3}x+\displaystyle \frac{{35+12}}{3}\\ & =-\displaystyle \frac{5}{3}x+\displaystyle \frac{{47}}{3}\end{align*}[/latex]

Here is a sketch of the two lines.

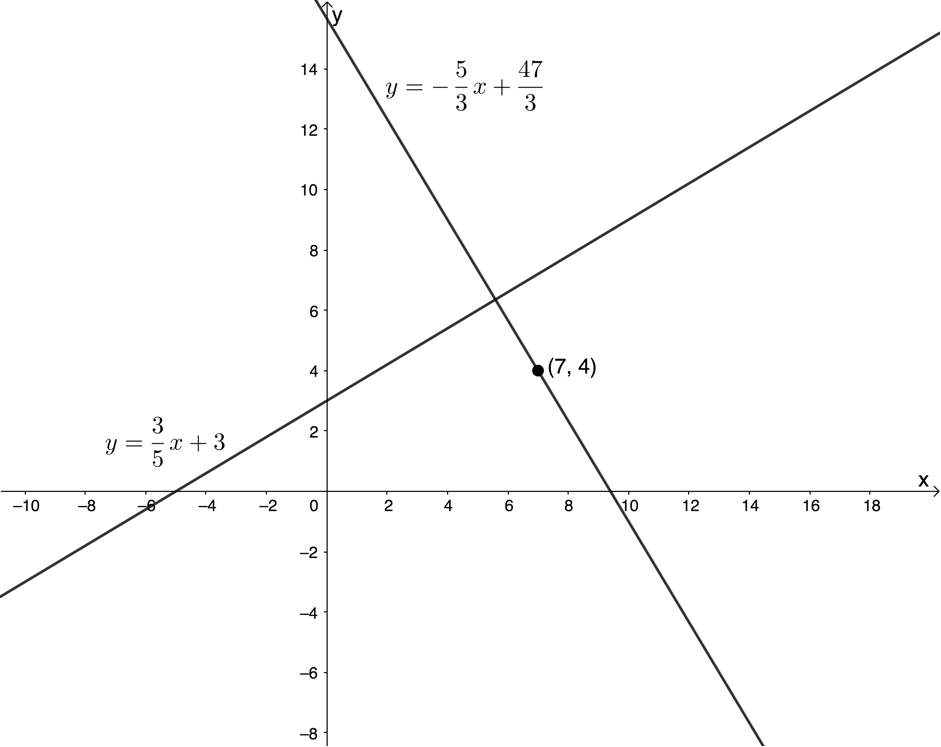
Exercise 2.2

1. Determine the equation of the following straight lines:
   1. passing through [latex]\scriptsize (2,-3)[/latex] and perpendicular to the line [latex]\scriptsize y+3x-4=0[/latex]
   2. passing through [latex]\scriptsize (-4,1)[/latex] and perpendicular to the line [latex]\scriptsize 3(y+2x)=7[/latex]
   3. passing through [latex]\scriptsize (-3,-3)[/latex] and perpendicular to the line passing through [latex]\scriptsize (4,2)[/latex] and [latex]\scriptsize (-2,6)[/latex]
2. Determine if the following straight lines are perpendicular or not:
   1. [latex]\scriptsize 4y+2=-x[/latex] and [latex]\scriptsize 4x=y-1[/latex]
   2. [latex]\scriptsize \displaystyle \frac{1}{3}y=x+3[/latex] and [latex]\scriptsize 3y+x=-9[/latex]
   3. [latex]\scriptsize y=2[/latex] and [latex]\scriptsize x=-3[/latex]
3. For what value of [latex]\scriptsize a[/latex] will [latex]\scriptsize y+\displaystyle \frac{x}{a}=c[/latex] and [latex]\scriptsize 2y-\displaystyle \frac{{3x}}{a}+k=0[/latex] be perpendicular?

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• If two straight lines on the Cartesian plane are parallel, then [latex]\scriptsize {{m}_{1}}={{m}_{2}}[/latex].
• If two straight lines on the Cartesian plane are perpendicular, then [latex]\scriptsize {{m}_{1}}\times {{m}_{2}}=-1[/latex].

Unit 2: Assessment

Suggested time to complete: 30 minutes

1. Determine the equation of the line that passes through the point [latex]\scriptsize (1,-1)[/latex] and is parallel to the line [latex]\scriptsize y-2x+1=0[/latex].
2. Determine the equation of the straight line that passes through the point [latex]\scriptsize (2,7)[/latex] and is perpendicular to the line [latex]\scriptsize 5y-x=0[/latex].

Question 3 is taken from NC(V) Mathematics Level 3 Paper 2 March 2013 question 1.3

3. [latex]\scriptsize A(2,3)[/latex] and [latex]\scriptsize B(-5,-2)[/latex] are points on the Cartesian plane. [latex]\scriptsize CD[/latex] is perpendicular to [latex]\scriptsize AB[/latex] and passes through the point [latex]\scriptsize (5,0)[/latex].
   1. Determine the gradient of line segment [latex]\scriptsize AB[/latex].
   2. Determine the equation of line segment [latex]\scriptsize CD[/latex].

Question 4 is taken from NC(V) Mathematics Level 3 Paper 2 March 2014 question 1.3

4. [latex]\scriptsize R(-4,2)[/latex] and [latex]\scriptsize T(2,4)[/latex] are points in the Cartesian plane. [latex]\scriptsize M[/latex] is the midpoint of [latex]\scriptsize RT[/latex].
   
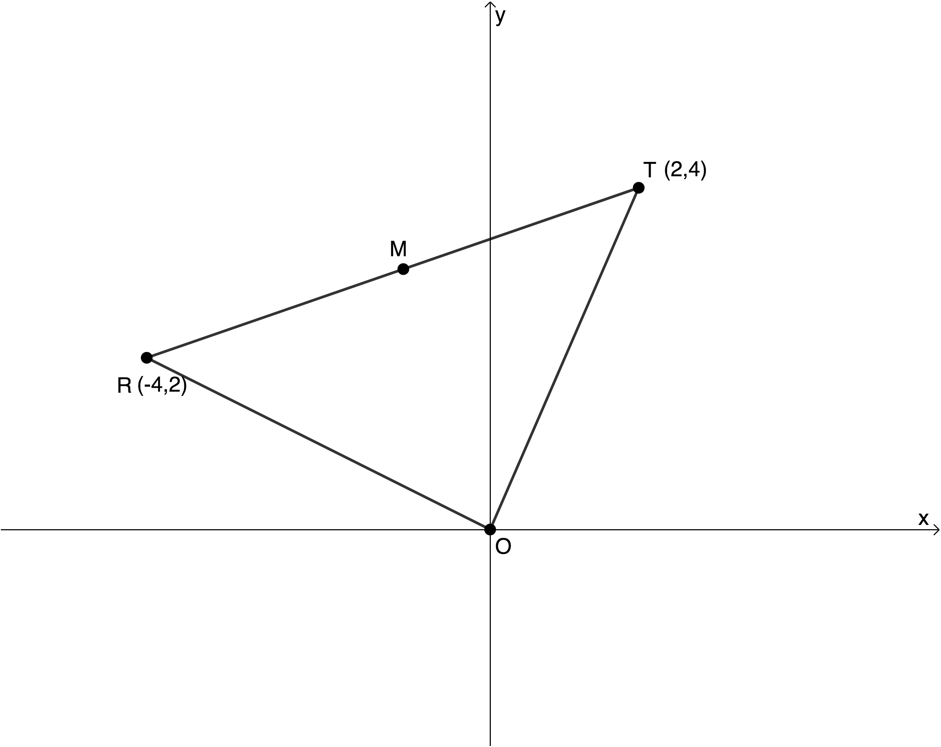
   1. Calculate the length of [latex]\scriptsize RT[/latex].
   2. Calculate the co-ordinates of [latex]\scriptsize M[/latex], the midpoint of [latex]\scriptsize RT[/latex].
   3. Write down the equation of [latex]\scriptsize OM[/latex].
   4. Show by calculation that [latex]\scriptsize \Delta ROT[/latex] is a right-angle triangle.

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. .
   1. .
      [latex]\scriptsize \begin{align*}y+3x-4 & =0\\\therefore y & =-3x+4\end{align*}[/latex]
      Therefore [latex]\scriptsize m=-3[/latex]
      [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-3) & =-3\left( {x-2} \right)\\\therefore y+3 & =-3x+6\\\therefore y & =-3x+3\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}3(y+2x) & =7\\\therefore 3y+6x & =7\\\therefore 3y & =-6x+7\\\therefore y & =-2x+\displaystyle \frac{7}{3}\end{align*}[/latex]
      Therefore [latex]\scriptsize m=-2[/latex]
      [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-1 & =-2\left( {x-(-4)} \right)\\\therefore y-1 & =-2(x+4)\\\therefore y-1 & =-2x-8\\\therefore y & =-2x-7\end{align*}[/latex]
   3. .
      Gradient of the line passing through [latex]\scriptsize (4,2)[/latex] and [latex]\scriptsize (-2,6)[/latex]:
      [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{6-2}}{{-2-4}}\\&=-\displaystyle \frac{4}{6}\\&=-\displaystyle \frac{2}{3}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-3) & =-\displaystyle \frac{2}{3}\left( {x-(-3)} \right)\\\therefore y+3 & =-\displaystyle \frac{2}{3}(x+3)\\\therefore y+3 & =-\displaystyle \frac{2}{3}x-2\\\therefore y & =-\displaystyle \frac{2}{3}x-5\end{align*}[/latex]
2. .
   1. .
      [latex]\scriptsize \begin{align*}y+3x & =8\\\therefore y & =-3x+8\end{align*}[/latex]
      Therefore, [latex]\scriptsize {{m}_{1}}=-3[/latex]
      [latex]\scriptsize \begin{align*}6x & =3y-2\\\therefore 3y & =6x+2\\\therefore y & =2x+\displaystyle \frac{2}{3}\end{align*}[/latex]
      Therefore, [latex]\scriptsize {{m}_{2}}=2[/latex]
      [latex]\scriptsize {{m}_{1}}\ne {{m}_{2}}[/latex]. Therefore, the lines are not parallel.
   2. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{y}{3}+x+5 & =0\\\therefore \displaystyle \frac{y}{3} & =-x-5\\\therefore y & =-3x-15\end{align*}[/latex]
      Therefore, [latex]\scriptsize {{m}_{1}}=-3[/latex]
      [latex]\scriptsize \begin{align*}2y+6x & =1\\\therefore 2y & =-6x+1\\\therefore y & =-3x+\displaystyle \frac{1}{2}\end{align*}[/latex]
      Therefore, [latex]\scriptsize {{m}_{2}}=-3[/latex]
      [latex]\scriptsize {{m}_{1}}={{m}_{2}}[/latex]. Therefore, the lines are parallel.
   3. .
      [latex]\scriptsize \begin{align*}y-1 & =\displaystyle \frac{1}{3}x\\\therefore y & =\displaystyle \frac{1}{3}x+1\end{align*}[/latex]
      Therefore, [latex]\scriptsize {{m}_{1}}=\displaystyle \frac{1}{3}[/latex]
      Line passing through [latex]\scriptsize (-2,4)[/latex] and [latex]\scriptsize (1,5)[/latex].
      [latex]\scriptsize \begin{align*}{{m}_{2}}&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{5-4}}{{1-(-2)}}\\&=\displaystyle \frac{1}{3}\end{align*}[/latex]
      [latex]\scriptsize {{m}_{1}}={{m}_{2}}[/latex]. Therefore, the lines are parallel.

Back to Exercise 2.1

Exercise 2.2

1. .
   1. Passing through [latex]\scriptsize (2,-3)[/latex] and perpendicular to the line [latex]\scriptsize y+3x-4=0[/latex].
      [latex]\scriptsize \begin{align*}y+3x-4 & =0\\\therefore y & =-3x+4\end{align*}[/latex]
      [latex]\scriptsize {{m}_{1}}=-3=-\displaystyle \frac{3}{1}[/latex]. Therefore, [latex]\scriptsize {{m}_{2}}=\displaystyle \frac{1}{3}[/latex].
      [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-3) & =\displaystyle \frac{1}{3}\left( {x-2} \right)\\\therefore y+3 & =\displaystyle \frac{1}{3}x-\displaystyle \frac{2}{3}\\\therefore y & =\displaystyle \frac{1}{3}x-\displaystyle \frac{2}{3}-\displaystyle \frac{9}{3}\\&=\displaystyle \frac{1}{3}x-\displaystyle \frac{{11}}{3}\end{align*}[/latex]
   2. Passing through [latex]\scriptsize (-4,1)[/latex] and perpendicular to the line [latex]\scriptsize 3(y+2x)=7[/latex].
      [latex]\scriptsize \begin{align*}3(y+2x) & =7\\\therefore 3y+6x & =7\\\therefore 3y & =-6x+7\\\therefore y & =-2x+\displaystyle \frac{7}{3}\end{align*}[/latex]
      [latex]\scriptsize {{m}_{1}}=-2=-\displaystyle \frac{2}{1}[/latex]. Therefore, [latex]\scriptsize {{m}_{2}}=\displaystyle \frac{1}{2}[/latex].
      [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-1 & =\displaystyle \frac{1}{2}\left( {x-(-4)} \right)\\\therefore y-1 & =\displaystyle \frac{1}{2}(x+4)\\\therefore y-1 & =\displaystyle \frac{1}{2}x+2\\\therefore y & =\displaystyle \frac{1}{2}x+3\end{align*}[/latex]
   3. Passing through [latex]\scriptsize (-3,-3)[/latex] and perpendicular to the line passing through [latex]\scriptsize (4,2)[/latex] and [latex]\scriptsize (-2,6)[/latex].
      Gradient of the line passing through [latex]\scriptsize (4,2)[/latex] and [latex]\scriptsize (-2,6)[/latex]:
      [latex]\scriptsize \begin{align*}m&=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\&=\displaystyle \frac{{6-2}}{{-2-4}}\\&=-\displaystyle \frac{4}{6}\\&=-\displaystyle \frac{2}{3}\end{align*}[/latex]
      [latex]\scriptsize {{m}_{1}}=-\displaystyle \frac{2}{3}[/latex]. Therefore, [latex]\scriptsize {{m}_{2}}=\displaystyle \frac{3}{2}[/latex]
      [latex]\scriptsize \begin{align*}y-{{y}_{1}} &=m(x-{{x}_{1}})\\\therefore y-(-3) &=\displaystyle \frac{3}{2}\left( {x-(-3)} \right)\\\therefore y+3 &=\displaystyle \frac{3}{2}(x+3)\\\therefore y+3 &=\displaystyle \frac{3}{2}x+\displaystyle \frac{9}{2}\\\therefore y &=\displaystyle \frac{3}{2}x+\displaystyle \frac{{9-6}}{2}\\&=\displaystyle \frac{3}{2}x+\displaystyle \frac{3}{2}\end{align*}[/latex]
2. .
   1. .
      [latex]\scriptsize \begin{align*}4y+2 & =-x\\\therefore 4y & =-x-2\\\therefore y & =-\displaystyle \frac{1}{4}x-\displaystyle \frac{1}{2}\end{align*}[/latex]
      [latex]\scriptsize {{m}_{1}}=-\displaystyle \frac{1}{4}[/latex]
      [latex]\scriptsize \begin{align*}4x & =y-1\\\therefore y & =4x+1\end{align*}[/latex]
      [latex]\scriptsize {{m}_{2}}=\displaystyle \frac{4}{1}[/latex]
      [latex]\scriptsize {{m}_{1}}\times {{m}_{2}}=-1[/latex]. Therefore, the lines are perpendicular.
   2. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{3}y & =x+3\\\therefore y & =3x+9\end{align*}[/latex]
      [latex]\scriptsize {{m}_{1}}=\displaystyle \frac{3}{1}[/latex]
      .
      [latex]\scriptsize \begin{align*}3y+x & =-9\\\therefore 3y & =-x-9\\\therefore y & =-\displaystyle \frac{1}{3}x-3\end{align*}[/latex]
      [latex]\scriptsize {{m}_{2}}=-\displaystyle \frac{1}{3}[/latex]
      [latex]\scriptsize {{m}_{1}}\times {{m}_{2}}=-1[/latex]. Therefore, the lines are perpendicular.
   3. [latex]\scriptsize y=2[/latex]. The line is horizontal. Therefore, [latex]\scriptsize {{m}_{1}}=0[/latex].
      [latex]\scriptsize x=-3[/latex]. The line is vertical. Therefore, [latex]\scriptsize {{m}_{2}}[/latex] is undefined.
      However, even though [latex]\scriptsize {{m}_{1}}\times {{m}_{2}}[/latex] cannot be calculated, we know the lines are perpendicular.
3. .
   [latex]\scriptsize \begin{align*}y+\displaystyle \frac{x}{a} & =c\\\therefore y & =-\displaystyle \frac{1}{a}x+c\end{align*}[/latex]
   [latex]\scriptsize {{m}_{1}}=-\displaystyle \frac{1}{a}[/latex]
   [latex]\scriptsize \begin{align*}2y-\displaystyle \frac{{3x}}{a}+k & =0\\\therefore 2y & =\displaystyle \frac{3}{a}x-k\\\therefore y & =\displaystyle \frac{3}{{2a}}x-\displaystyle \frac{k}{2}\end{align*}[/latex]
   [latex]\scriptsize {{m}_{2}}=\displaystyle \frac{3}{{2a}}[/latex]
   For perpendicular lines [latex]\scriptsize {{m}_{1}}\times {{m}_{2}}=-1[/latex]:
   [latex]\scriptsize \begin{align*}-\displaystyle \frac{1}{a}\times \displaystyle \frac{3}{{2a}} & =-1,a\ne 0\\\therefore \displaystyle \frac{{-3}}{{2{{a}^{2}}}} & =-1\\\therefore -3 & =-2{{a}^{2}}\\\therefore 2{{a}^{2}} & =3\\\therefore {{a}^{2}} & =\displaystyle \frac{3}{2}\\\therefore a & =\pm \sqrt{{\displaystyle \frac{3}{2}}}\end{align*}[/latex]

Back to Exercise 2.2

Unit 2: Assessment

1. .
   [latex]\scriptsize \begin{align*}y-2x+1 & =0\\\therefore y & =2x-1\end{align*}[/latex]
   [latex]\scriptsize {{m}_{1}}=2[/latex]. Therefore [latex]\scriptsize {{m}_{2}}=2[/latex].
   [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-(-1) & =2(x-1)\\\therefore y+1 & =2x-2\\\therefore y & =2x-3\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}5y-x & =0\\\therefore 5y & =x\\\therefore y & =\displaystyle \frac{1}{5}x\end{align*}[/latex]
   [latex]\scriptsize {{m}_{1}}=\displaystyle \frac{1}{5}[/latex]. Therefore, [latex]\scriptsize {{m}_{2}}=-5[/latex].
   [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-7 & =-5(x-2)\\\therefore y-7 & =-5x+10\\\therefore y & =-5x+17\end{align*}[/latex]
3. [latex]\scriptsize A(2,3)[/latex] and [latex]\scriptsize B(-5,-2)[/latex] are points on the Cartesian plane. [latex]\scriptsize CD[/latex] is perpendicular to [latex]\scriptsize AB[/latex] and passes through the point [latex]\scriptsize (5,0)[/latex].
   1. [latex]\scriptsize {{m}_{{AB}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{-2-3}}{{-5-2}}=\displaystyle \frac{5}{7}[/latex]
   2. [latex]\scriptsize {{m}_{{CD}}}=-\displaystyle \frac{7}{5}[/latex]
      [latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-0 & =-\displaystyle \frac{7}{5}(x-5)\\\therefore y & =-\displaystyle \frac{7}{5}x+7\end{align*}[/latex]
4. .
   1. .
      [latex]\scriptsize \begin{align*}RT&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{\left( {2-(-4)} \right)}}^{2}}+{{{\left( {4-2} \right)}}^{2}}}}\\&=\sqrt{{{{6}^{2}}+{{2}^{2}}}}\\&=\sqrt{{36+4}}\\&=\sqrt{{40}}\\&=2\sqrt{{10}}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}M&=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\\&=\left( {\displaystyle \frac{{-4+2}}{2},\displaystyle \frac{{2+4}}{2}} \right)\\&=\left( {\displaystyle \frac{{-2}}{2},\displaystyle \frac{6}{2}} \right)\\&=(-1,3)\end{align*}[/latex]
   3. [latex]\scriptsize O(0,0)[/latex]
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\\therefore \displaystyle \frac{{y-0}}{{x-0}} & =\displaystyle \frac{{3-0}}{{-1-0}}\\\therefore \displaystyle \frac{y}{x} & =-3\\\therefore y & =-3x\end{align*}[/latex]
   4. [latex]\scriptsize {{m}_{{RO}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{2-0}}{{-4-0}}=-\displaystyle \frac{1}{2}[/latex]
      [latex]\scriptsize {{m}_{{TO}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{4-0}}{{2-0}}=\displaystyle \frac{2}{1}[/latex]
      [latex]\scriptsize {{m}_{{RO}}}\times {{m}_{{TO}}}=-1[/latex]. Therefore [latex]\scriptsize R\hat{O}T={{90}^\circ}[/latex].

Back to Unit 2: Assessment