Unit outcomes

By the end of this unit you will be able to:

• Use the sine rule to find an unknown length of a triangle.
• Use the sine rule to find an unknown angle of a triangle.

What you should know

Before you start this unit, make sure you can:

• State and use the area rule. Refer to unit 5 of this subject outcome if you need help with this.
• Use a calculator to calculate the sine of a given angle. Refer to level 2 subject outcome 3.6 unit 2 if you need help with this.
• Use a calculator to calculate the angle from a given ratio for sine. Refer to level 2 subject outcome 3.6 unit 2 if you need help with this.
• Solve simple linear equations.

Introduction

In the previous unit, we derived and used the area rule – a useful trig identity that lets us calculate the area of any triangle if we know the length of any two sides and the size of the included angle.

In [latex]\scriptsize \Delta ABC[/latex]:

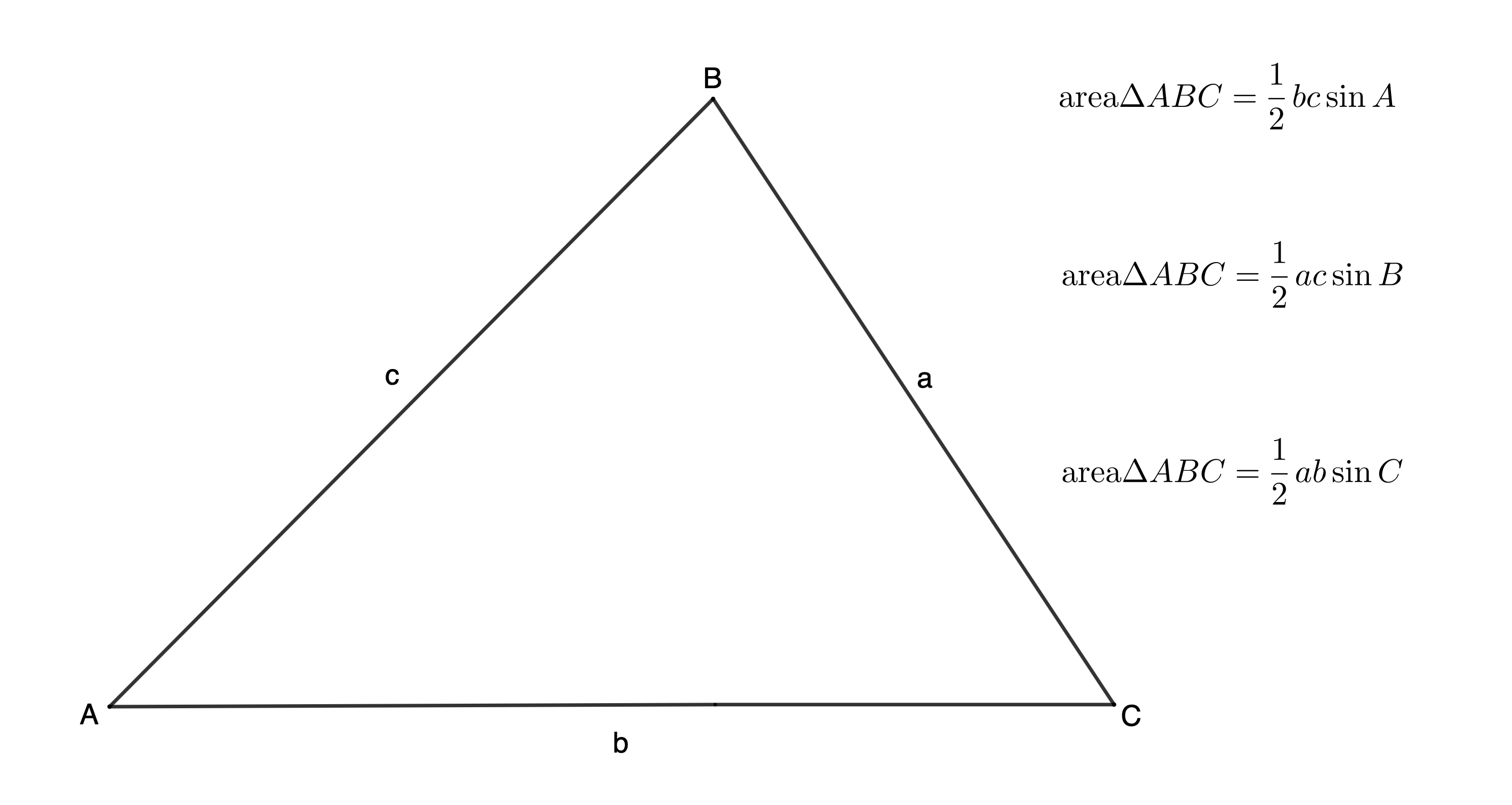
Figure 1: The area ruleEach of these statements for the area of [latex]\scriptsize \Delta ABC[/latex] must be equal – they all give the area of the very same triangle. Therefore, we can write that:
[latex]\scriptsize \begin{align*}\text{Area }\Delta ABC & =\displaystyle \frac{1}{2}bc\sin A=\displaystyle \frac{1}{2}ac\sin B=\displaystyle \frac{1}{2}ab\sin C\\\therefore bc\sin A & =ac\sin B=ab\sin C\end{align*}[/latex]

Now, if we divide through by [latex]\scriptsize abc[/latex] we get the following:
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\bcancel{b}\bcancel{c}\sin A}}{{a\bcancel{b}\bcancel{c}}} & =\displaystyle \frac{{\bcancel{a}\bcancel{c}\sin B}}{{\bcancel{a}b\bcancel{c}}}=\displaystyle \frac{{\bcancel{a}\bcancel{b}\sin C}}{{\bcancel{a}\bcancel{b}c}}\\\therefore \displaystyle \frac{{\sin A}}{a} & =\displaystyle \frac{{\sin B}}{b}=\displaystyle \frac{{\sin C}}{c}\end{align*}[/latex]

This trig identity is called the sine rule. It is very useful for finding missing sides and angles of triangles, as we shall see.

The sine rule

Let’s now look at the sine rule in more detail.

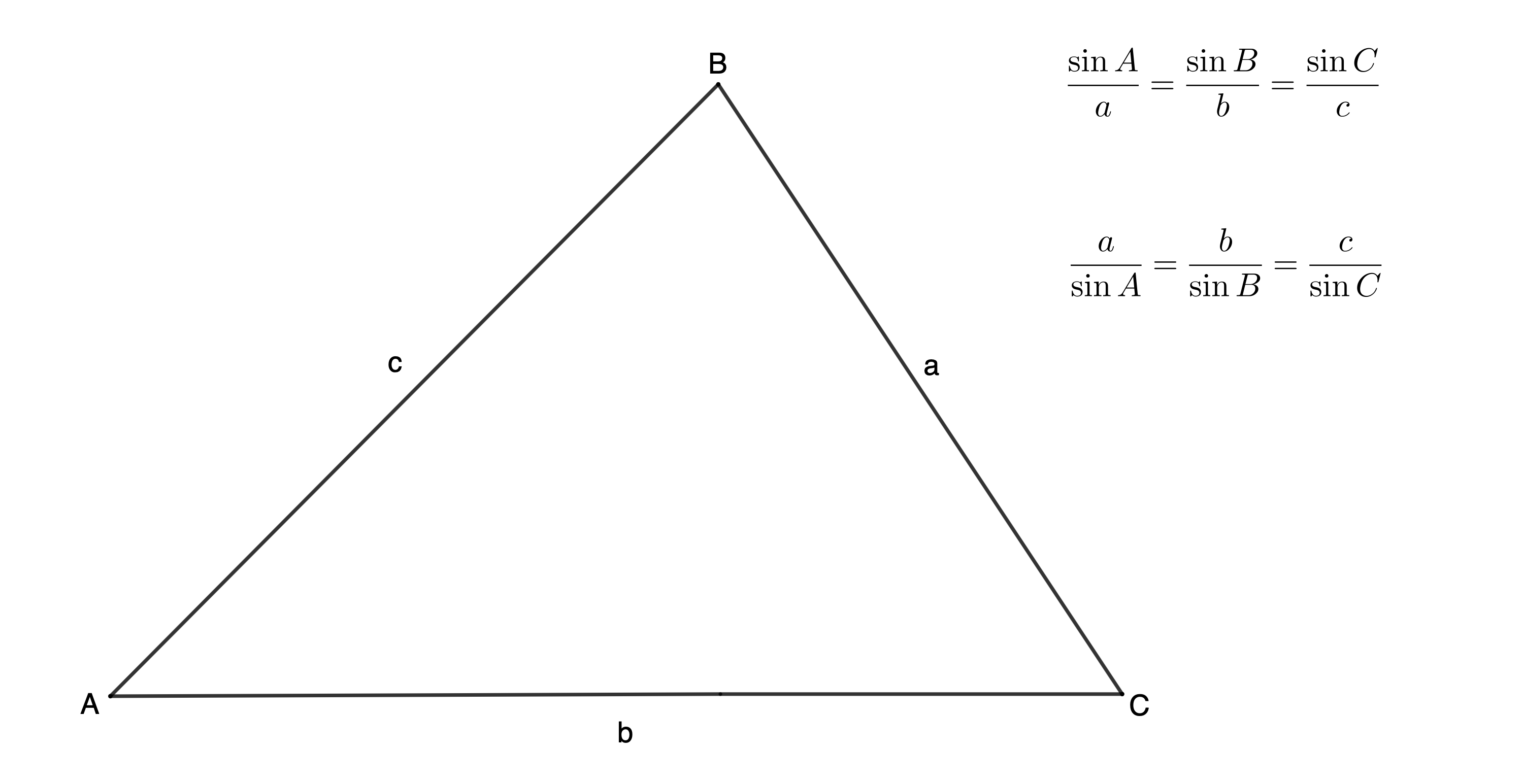
Take note!

You must make sure that you get the naming of vertices and sides in your triangle correct. The side opposite vertex [latex]\scriptsize A[/latex] is [latex]\scriptsize a[/latex]. The side opposite vertex [latex]\scriptsize B[/latex] is [latex]\scriptsize b[/latex]. The side opposite vertex [latex]\scriptsize C[/latex] is [latex]\scriptsize c[/latex]. The sine rule will only work if you label your triangle like this.

Take note!

The sine rule can also be expressed in reciprocal form.

[latex]\scriptsize \displaystyle \frac{a}{{\sin A}}=\displaystyle \frac{b}{{\sin B}}=\displaystyle \frac{c}{{\sin C}}[/latex]

Example 6.1

Find all the missing sides and angles.

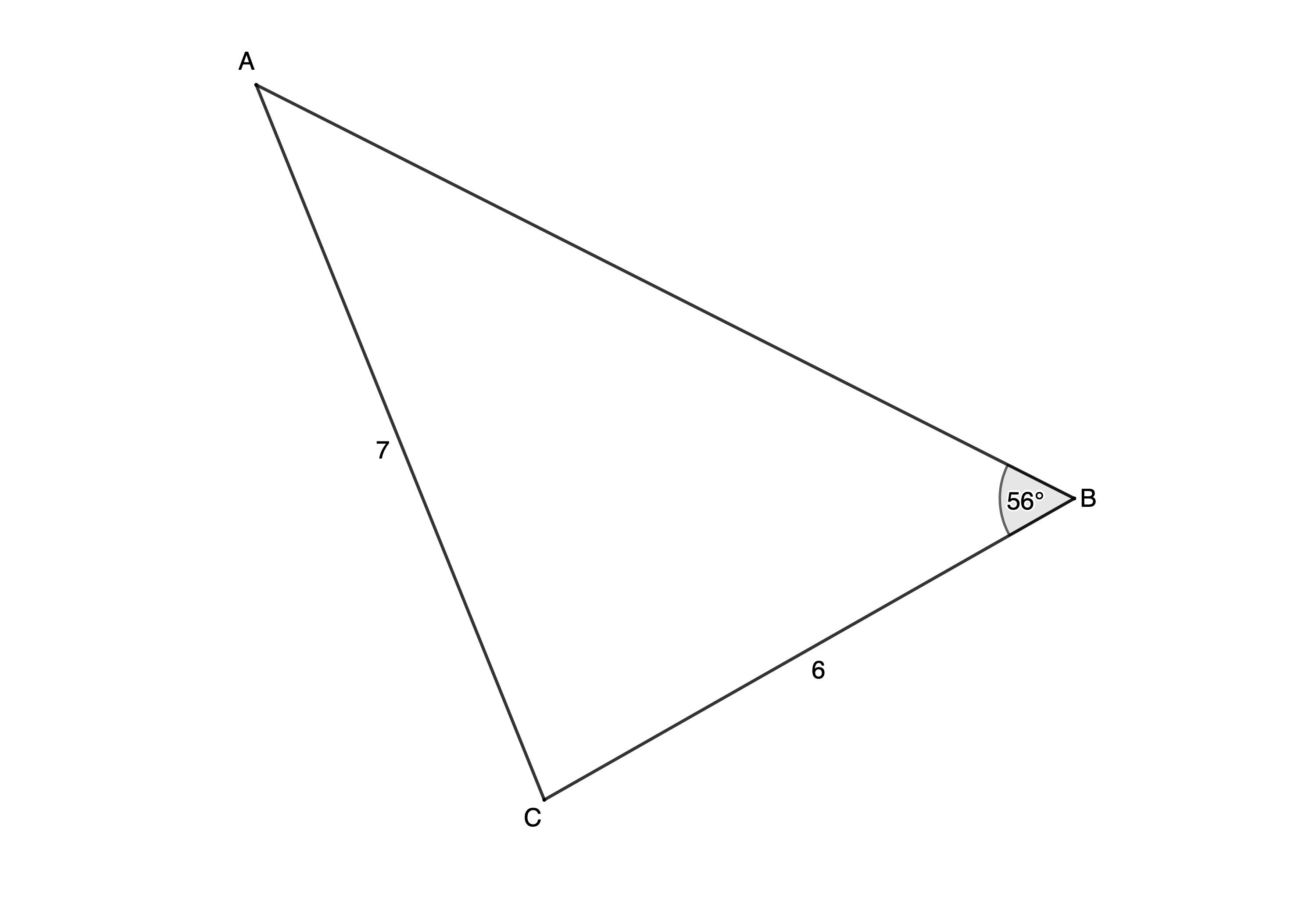
Solution

We have been given [latex]\scriptsize \hat{B}={{56}^\circ}[/latex], [latex]\scriptsize b=7[/latex] and [latex]\scriptsize a=6[/latex]. We need to find the length of [latex]\scriptsize c[/latex] and the size of angles [latex]\scriptsize \hat{A}[/latex] and [latex]\scriptsize \hat{C}[/latex]. To do this, we can use the sine rule.

To use the sine rule we need to know three of the four unknowns. Therefore, we can use the information we have been given to find [latex]\scriptsize \hat{A}[/latex].

[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin A}}{a} & =\displaystyle \frac{{\sin B}}{b}\\\therefore \displaystyle \frac{{\sin A}}{6} & =\displaystyle \frac{{\sin {{{56}}^\circ}}}{7}\\\therefore \sin A & =\displaystyle \frac{{6\times \sin {{{56}}^\circ}}}{7}\\\therefore \hat{A} & ={{45.28}^\circ}\end{align*}[/latex]

Now that we have [latex]\scriptsize \hat{A}[/latex], we can find [latex]\scriptsize \hat{C}[/latex].
[latex]\scriptsize \begin{align*}\hat{C}&={{180}^\circ}-\hat{A}-\hat{B}&&\text{(angles in a triangle are supplementary)}\\ &={{180}^\circ}-{{45.28}^\circ}-{{56}^\circ}\\ &={{78.72}^\circ}\end{align*}[/latex]

Now we can use either [latex]\scriptsize \hat{A}/a[/latex] or [latex]\scriptsize \hat{B}/b[/latex] to find the length of [latex]\scriptsize c[/latex]. Because, we are finding a side, it is easier to use the reciprocal of the sine rule.
[latex]\scriptsize \begin{align*}\displaystyle \frac{b}{{\sin B}} & =\displaystyle \frac{c}{{\sin C}}\\\therefore \displaystyle \frac{7}{{\sin {{{56}}^\circ}}} & =\displaystyle \frac{c}{{\sin {{{78.72}}^\circ}}}\\\therefore c & =\displaystyle \frac{{7\times \sin {{{78.72}}^\circ}}}{{\sin {{{56}}^\circ}}}\\\therefore c & =8.28\end{align*}[/latex]

The ambiguous case

In [latex]\scriptsize \Delta ABC[/latex], [latex]\scriptsize \hat{B}={{32}^\circ}[/latex], [latex]\scriptsize b=6[/latex] and [latex]\scriptsize c=9[/latex]. Make a quick sketch of this triangle using the given information. Don’t read on until you have made your sketch. It does not need to be very accurate. Just a rough sketch will do.

Now look at Figures 2 and 3. Which one of these two triangles did yours look like? Which one is correct?

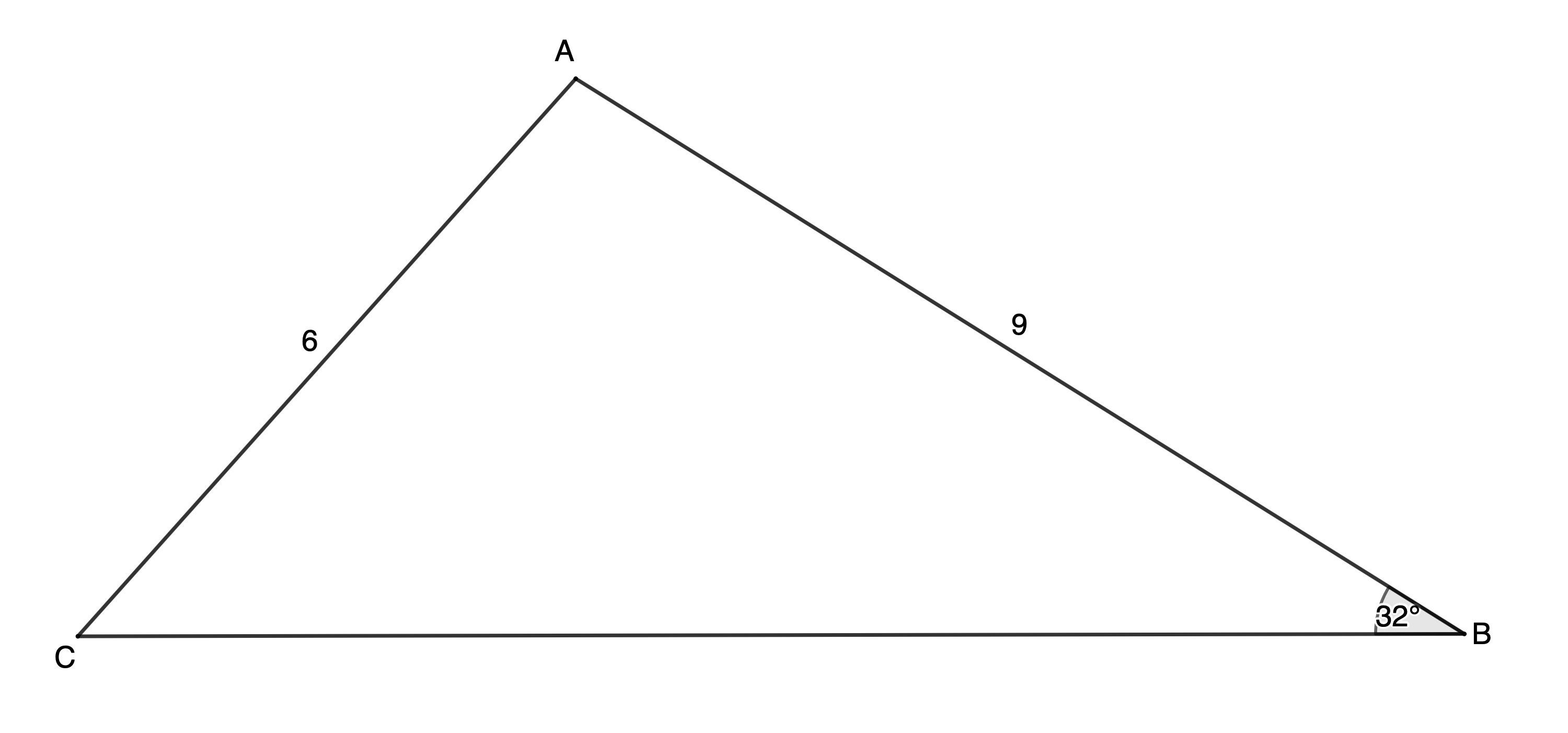
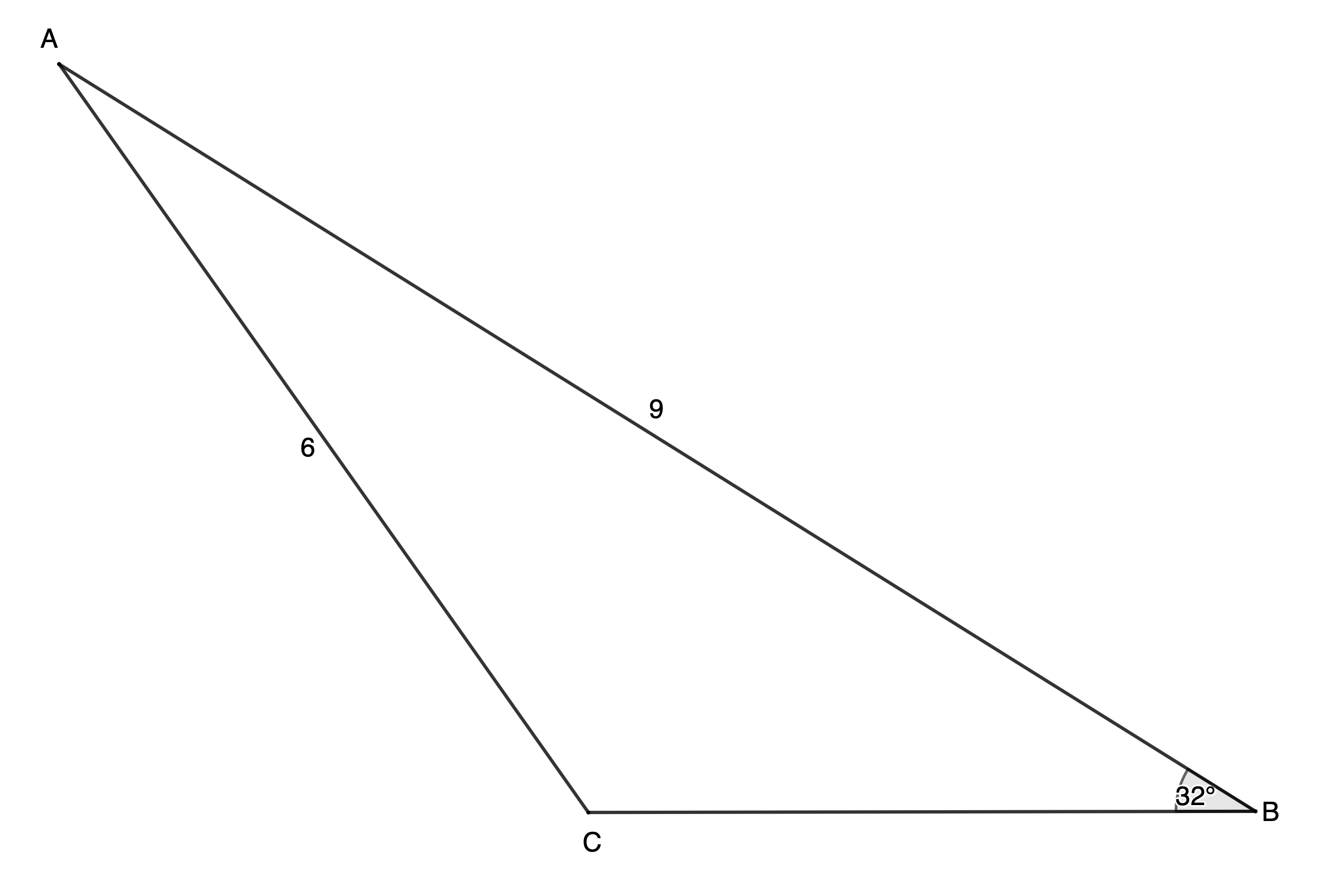
Can you see that both of them are correct interpretations of the information that was given? The differences are that the sizes of [latex]\scriptsize \hat{A}[/latex] and [latex]\scriptsize \hat{C}[/latex] and the length of [latex]\scriptsize a[/latex] in each case are different. This is an example of the ambiguous case and is a result of the fact that [latex]\scriptsize \sin \theta =\sin ({{180}^\circ}-\theta )[/latex]. In Figure 3 [latex]\scriptsize {{90}^\circ}\le \hat{C}\le {{180}^\circ}[/latex] and in Figure 2 [latex]\scriptsize 0^\circ\le\hat{C}\le90^\circ[/latex].

The ambiguous case happens when you are given two sides and an angle but the side opposite the given angle is the shorter of the two sides.

Example 6.2

In [latex]\scriptsize \Delta PQR[/latex], [latex]\scriptsize \hat{Q}={{43}^\circ}[/latex], [latex]\scriptsize r=7[/latex] and [latex]\scriptsize q=5[/latex]. Find the sizes of [latex]\scriptsize \hat{R}[/latex] and [latex]\scriptsize \hat{P}[/latex] and the length of [latex]\scriptsize p[/latex].

Solution

This is an example of the ambiguous case although you might not be able to recognise it immediately. It always helps to make a quick sketch of the given information. If you do, you will notice that there are two possible triangles based on the information given.

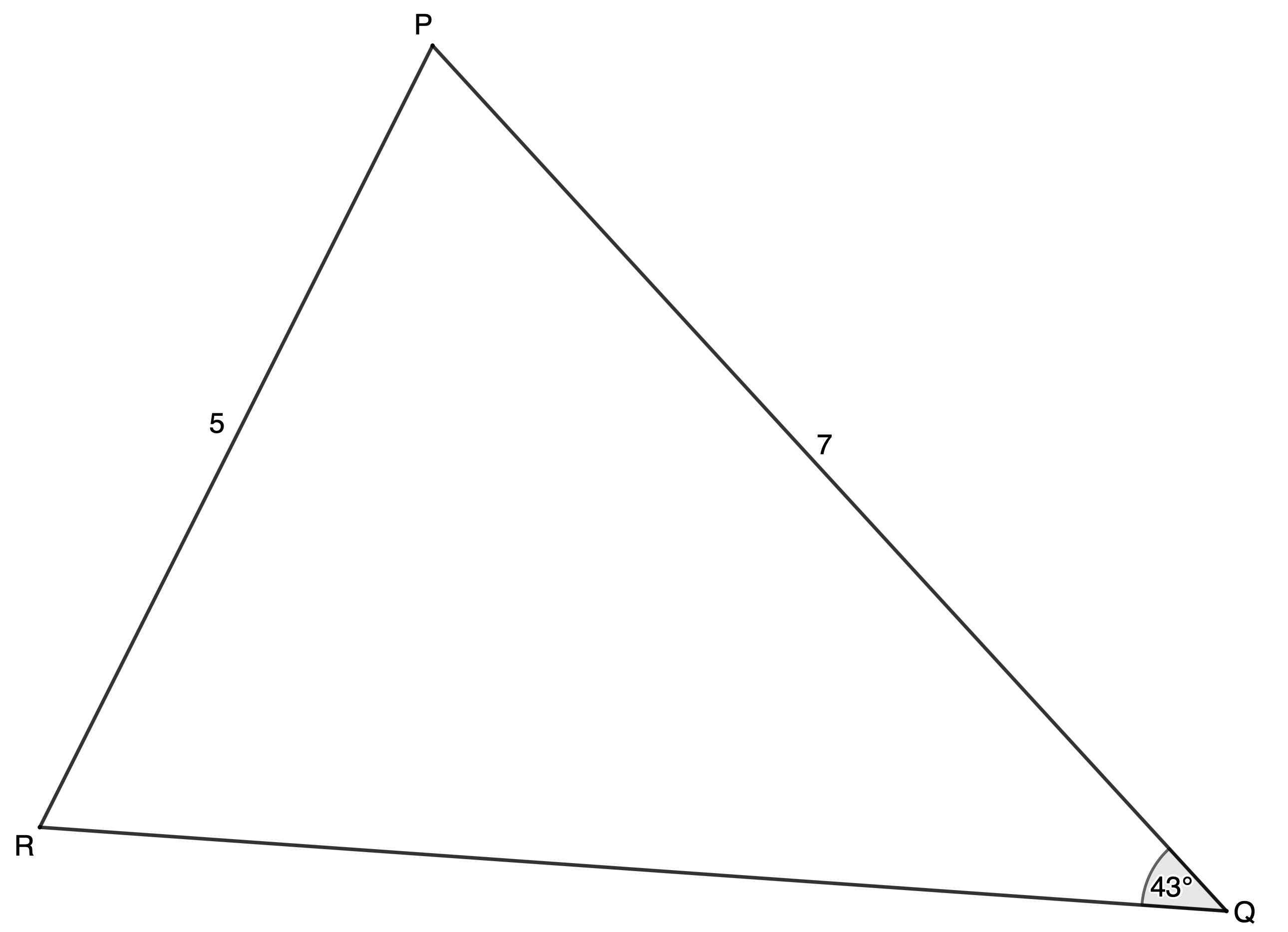
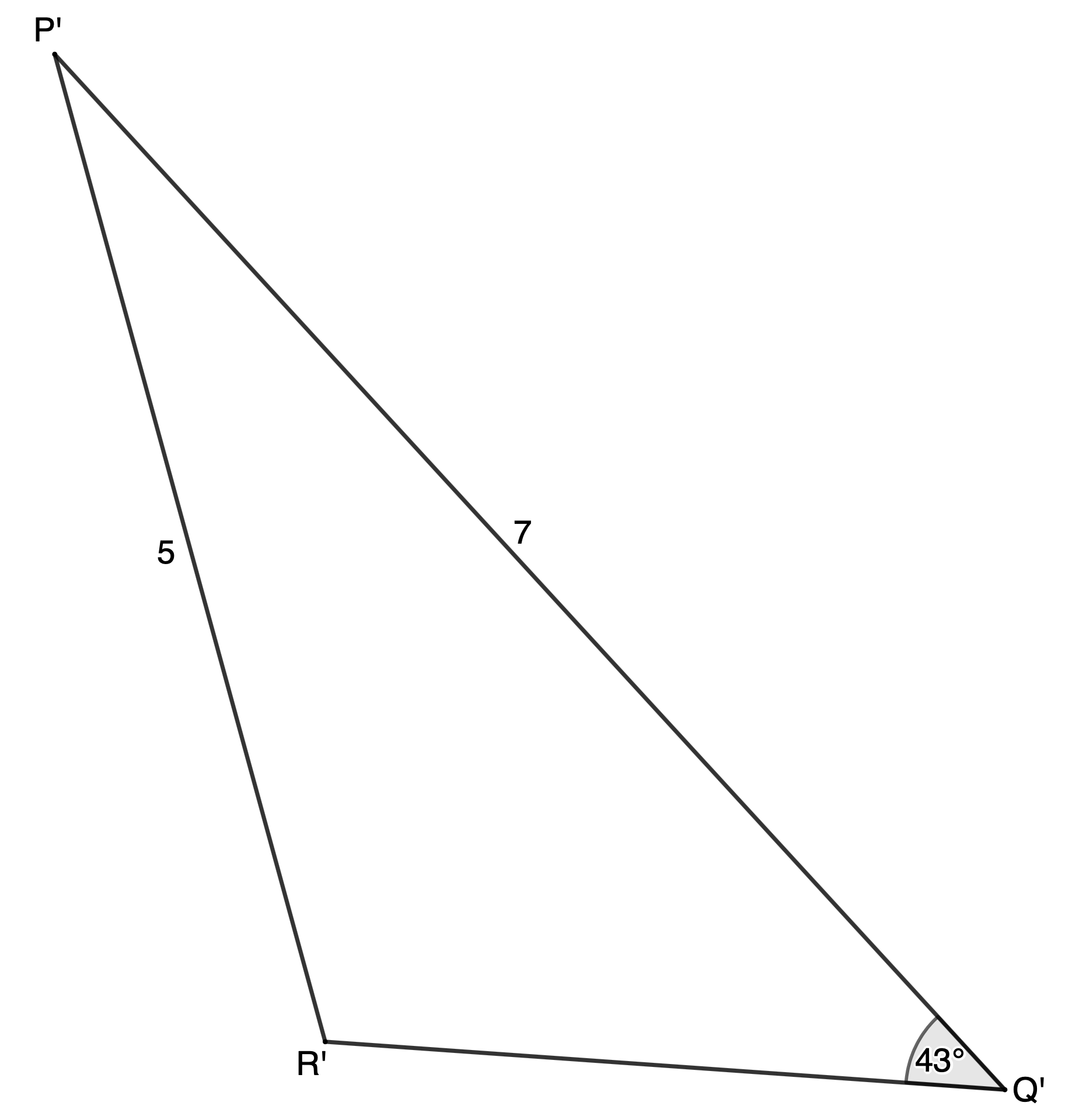
Remember, if the side opposite the given angle is the shorter side, then you have the ambiguous case. Here we can see that it is [latex]\scriptsize \hat{R}[/latex] that is either acute or obtuse.

[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin R}}{r}&=\displaystyle \frac{{\sin Q}}{q}\\\therefore \displaystyle \frac{{\sin R}}{7}&=\displaystyle \frac{{\sin 43{}^\circ }}{5}\\\therefore \sin R&=\displaystyle \frac{{7\times \sin 43{}^\circ }}{5}\text{ equation (1)}\end{align*}[/latex]

There are two solutions to this equation: since sine is positive in the first and second quadrants, so [latex]\scriptsize R[/latex] can be acute or obtuse.

Firstly, in [latex]\scriptsize \Delta PQR[/latex][latex]\scriptsize \hat{R}[/latex] is acute:
[latex]\scriptsize \begin{align*}\hat{R}&=72.71{}^\circ&&\text{(angles in a triangle are supplementary)}\\ \therefore P&={{180}^\circ}-{{72.71}^\circ}-{{43}^\circ}\\ &={{64.29}^\circ}\end{align*}[/latex]

[latex]\scriptsize \begin{align*}\displaystyle \frac{p}{{\sin P}} & =\displaystyle \frac{q}{{\sin Q}}\\\therefore \displaystyle \frac{p}{{\sin {{{64.29}}^\circ}}} & =\displaystyle \frac{5}{{\sin {{{43}}^\circ}}}\\\therefore p & =\displaystyle \frac{{5\times \sin {{{64.29}}^\circ}}}{{\sin {{{43}}^\circ}}}\\\therefore p & =6.61\end{align*}[/latex]

Now we can start working in the other possible triangle [latex]\scriptsize \Delta P'Q'R'[/latex] (where [latex]\scriptsize \hat{R}[/latex] is obtuse).
In [latex]\scriptsize \Delta P'Q'R'[/latex], and from equation (1) above:

[latex]\scriptsize \begin{align*}\hat{R}'={{180}^\circ}-{{72.71}^\circ}\\={{107.29}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\therefore P' & ={{180}^\circ}-{{107.29}^\circ}-{{43}^\circ}&&\text{(angles in a triangle are supplementary)}\\ & ={{29.71}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\displaystyle \frac{{p'}}{{\sin P'}} & =\displaystyle \frac{{q'}}{{\sin Q'}}\\\therefore \displaystyle \frac{{p'}}{{\sin {{{29.71}}^\circ}}} & =\displaystyle \frac{5}{{\sin {{{43}}^\circ}}}\\\therefore p' & =\displaystyle \frac{{5\times \sin {{{29.71}}^\circ}}}{{\sin {{{43}}^\circ}}}\\\therefore p' & =3.63\end{align*}[/latex]

Take note!

The ambiguous case occurs when you are given two sides and an angle but the side opposite the given angle is the shorter of the two sides.

Example 6.3

This question is adapted from Everything Maths Grade 11 Worked example 27

There is a coastline with two lighthouses, [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex], that are [latex]\scriptsize 0.73\ \text{km}[/latex] apart. [latex]\scriptsize B[/latex] is exactly due east of [latex]\scriptsize A[/latex]. The lighthouses can tell how close a boat ([latex]\scriptsize C[/latex]) is to the shore by taking bearings on the boat. These bearings are shown on the diagram below. How far is the boat from each lighthouse?

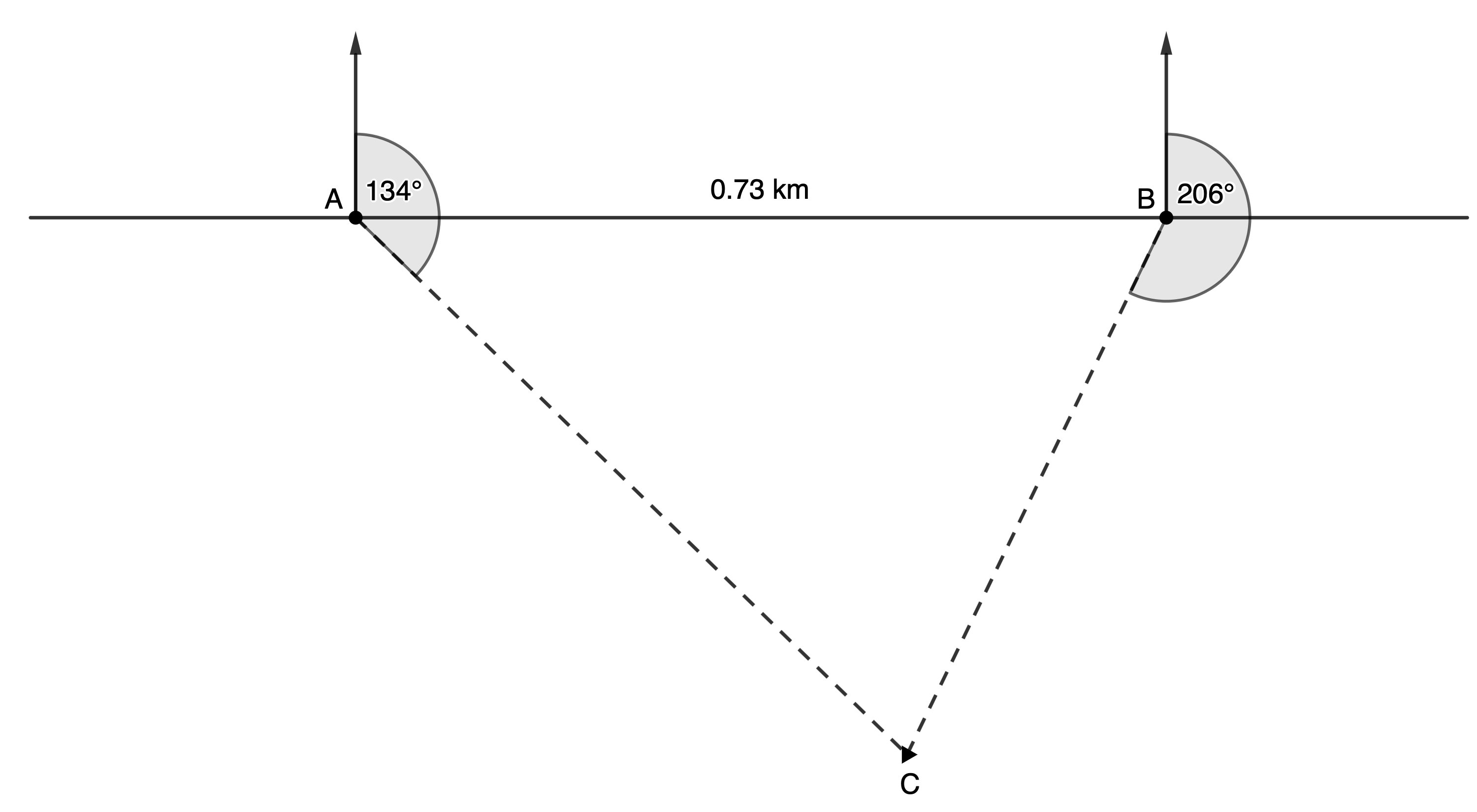
Solution

We need to calculate the distances [latex]\scriptsize AC[/latex] and [latex]\scriptsize BC[/latex]. First, we need to calculate the size of [latex]\scriptsize \hat{C}[/latex].
[latex]\scriptsize B\hat{A}C={{134}^\circ}-{{90}^\circ}={{44}^\circ}[/latex] (angles on a straight line)
[latex]\scriptsize A\hat{B}C={{360}^\circ}-{{90}^\circ}-{{206}^\circ}={{64}^\circ}[/latex] (angles around a point)
[latex]\scriptsize \therefore A\hat{C}B={{180}^\circ}-{{64}^\circ}-{{44}^\circ}={{72}^\circ}[/latex] (angles in a triangle are supplementary)

Side [latex]\scriptsize AC[/latex] is opposite [latex]\scriptsize A\hat{B}C[/latex], therefore we will refer to it as [latex]\scriptsize b[/latex].
Side [latex]\scriptsize BC[/latex] is opposite [latex]\scriptsize B\hat{A}C[/latex], therefore we will refer to it as [latex]\scriptsize a[/latex].
Side [latex]\scriptsize AB[/latex] is opposite [latex]\scriptsize A\hat{C}B[/latex], therefore we will refer to it as [latex]\scriptsize c[/latex].

[latex]\scriptsize \begin{align*}\displaystyle \frac{a}{{\sin B\hat{A}C}} & =\displaystyle \frac{c}{{\sin A\hat{C}B}}\\\therefore \displaystyle \frac{a}{{\sin {{{44}}^\circ}}} & =\displaystyle \frac{{0.73}}{{\sin {{{72}}^\circ}}}\\\therefore a & =\displaystyle \frac{{0.73\sin {{{44}}^\circ}}}{{\sin {{{72}}^\circ}}}\\ & =0.53\end{align*}[/latex]

[latex]\scriptsize \begin{align*}\displaystyle \frac{b}{{\sin A\hat{B}C}} & =\displaystyle \frac{c}{{\sin A\hat{C}B}}\\\therefore \displaystyle \frac{b}{{\sin {{{64}}^\circ}}} & =\displaystyle \frac{{0.73}}{{\sin {{{72}}^\circ}}}\\\therefore b & =\displaystyle \frac{{0.73\sin {{{64}}^\circ}}}{{\sin {{{72}}^\circ}}}\\ & =0.69\end{align*}[/latex]

The boat is [latex]\scriptsize 0.53\ \text{km}=530\ \text{m}[/latex] away from lighthouse [latex]\scriptsize B[/latex] and [latex]\scriptsize 0.69\ \text{km}=690\ \text{m}[/latex] away from lighthouse [latex]\scriptsize A[/latex].

Exercise 6.1

1. Find all the unknown sides and angles in the following triangles. Round all answers to two decimal places:
   1. [latex]\scriptsize \Delta ABC[/latex] where [latex]\scriptsize \hat{A}={{68}^\circ}[/latex], [latex]\scriptsize \hat{B}={{48}^\circ}[/latex] and [latex]\scriptsize b=7[/latex]
   2. [latex]\scriptsize \Delta PQR[/latex] where [latex]\scriptsize \hat{P}={{33}^\circ}[/latex], [latex]\scriptsize \hat{R}={{58}^\circ}[/latex] and [latex]\scriptsize p=6[/latex]
   3. [latex]\scriptsize \Delta STU[/latex] where [latex]\scriptsize \hat{U}={{34}^\circ}[/latex], [latex]\scriptsize u=9[/latex] and [latex]\scriptsize s=15[/latex]
   4. [latex]\scriptsize \Delta LMN[/latex] where [latex]\scriptsize \widehat{L}={{87}^\circ}[/latex], [latex]\scriptsize l=13[/latex] and [latex]\scriptsize n=10[/latex]

Question 2 is adapted from NC(V) Mathematics Level 3 Paper 2 November 2011 question 1.7

2. In the figure, [latex]\scriptsize A\hat{C}D={{90}^\circ}[/latex], [latex]\scriptsize A\hat{D}B={{20}^\circ}[/latex], [latex]\scriptsize B\hat{D}C={{25}^\circ}[/latex] and [latex]\scriptsize BC=10.5\ \text{cm}[/latex]. Let [latex]\scriptsize D\hat{A}B=x[/latex].
   
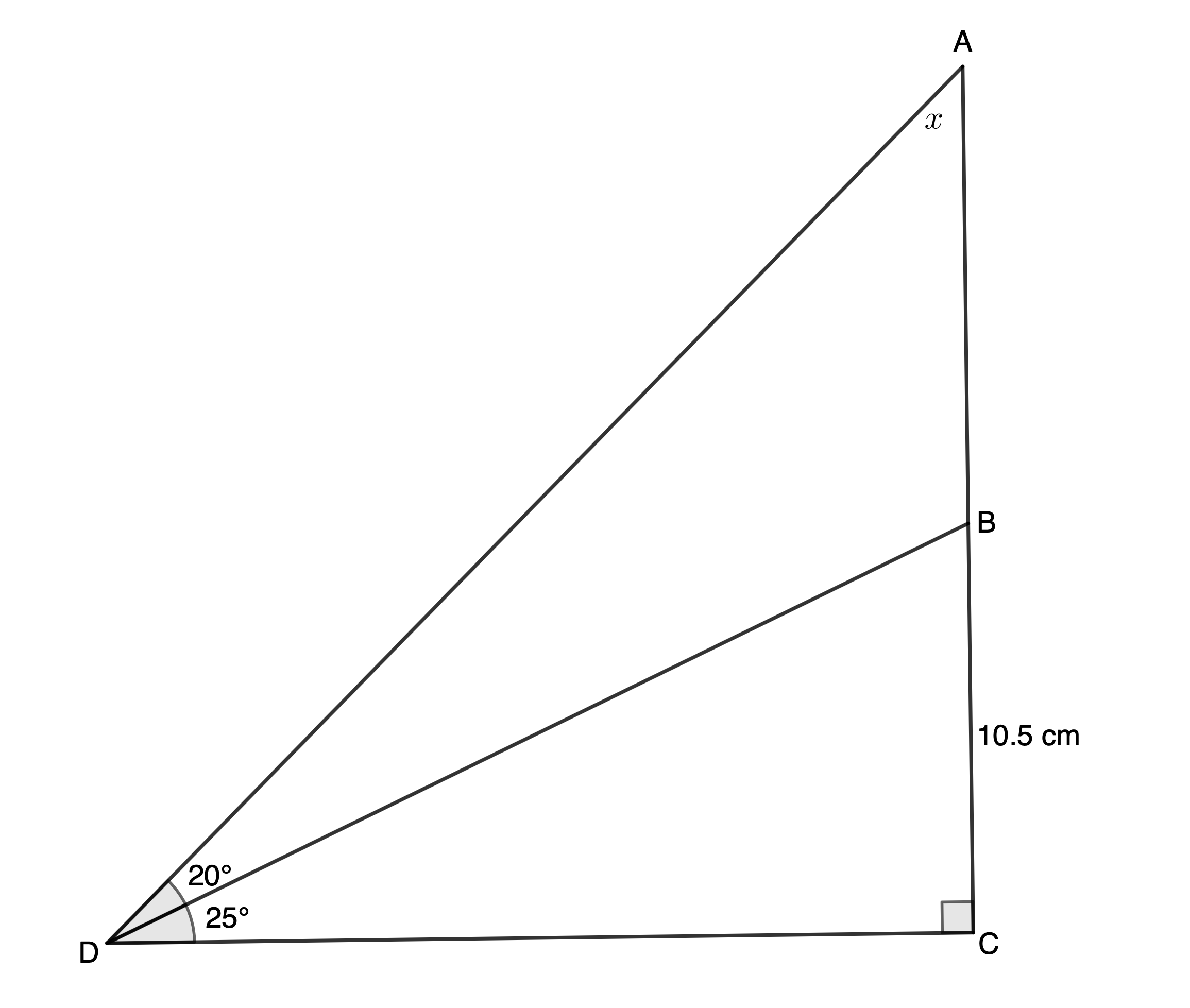
   1. Calculate the value of [latex]\scriptsize x[/latex].
   2. Determine the length of [latex]\scriptsize DB[/latex].
   3. Determine the length of [latex]\scriptsize AB[/latex].

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to find an unknown angle in a triangle using the sine rule.
• How to find an unknown side of a triangle using the sine rule.
• How to recognise and deal with the ambiguous case when solving triangles using the sine rule.

Unit 6: Assessment

Suggested time to complete: 45 minutes

Question 1 is adapted from NC(V) Mathematics Level 3 Paper 2 March 2014 question 2.6

1. In [latex]\scriptsize \Delta ABD[/latex], [latex]\scriptsize DA\bot AB[/latex] and [latex]\scriptsize AH\bot BD[/latex]. [latex]\scriptsize AB=10\ \text{cm}[/latex] and [latex]\scriptsize \hat{B}={{23}^\circ}[/latex].
   
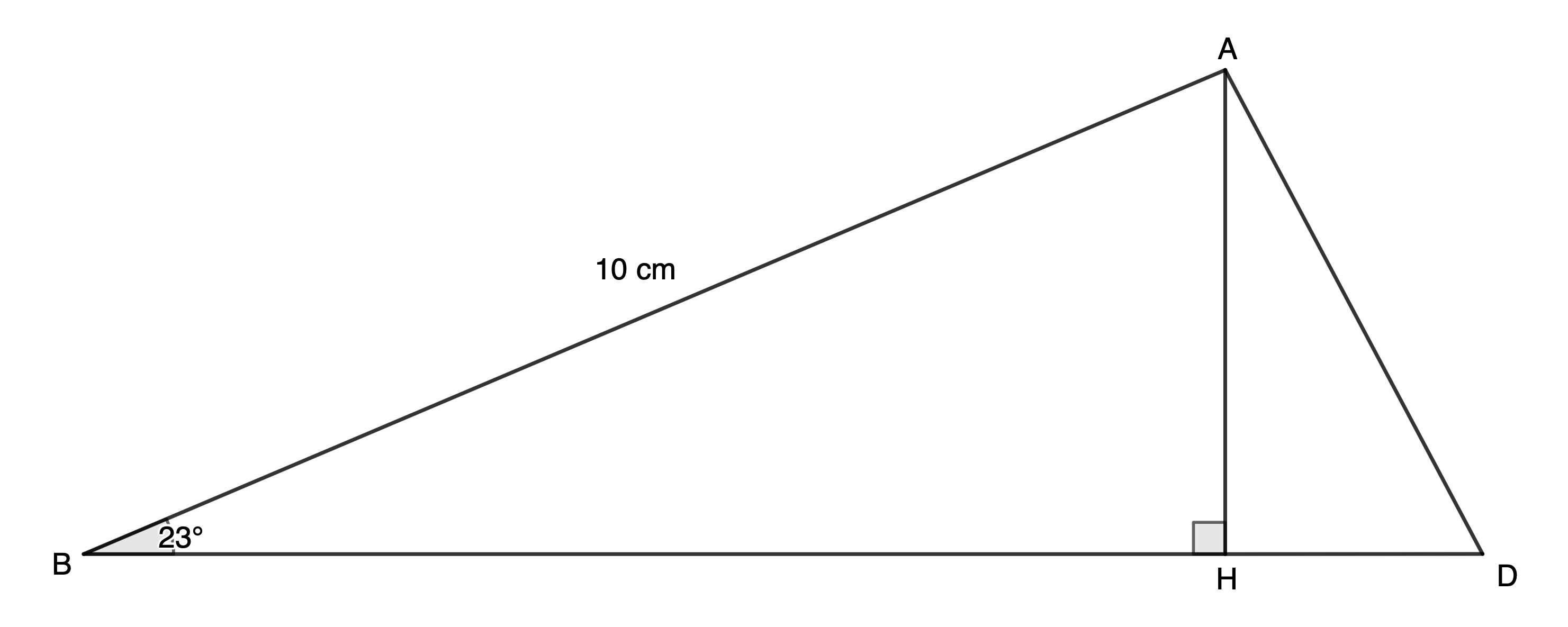
   1. Calculate the length of [latex]\scriptsize AH[/latex].
   2. Calculate the length of [latex]\scriptsize HD[/latex].

Question 2 is adapted from NC(V) Mathematics Level 3 Paper 2 March 2014 question 2.7

2. Below is a diagram of a farm in the shape of a quadrilateral. A fence from [latex]\scriptsize B[/latex] to [latex]\scriptsize D[/latex] divides the farm into two sections. [latex]\scriptsize AD=11\ \text{km}[/latex] and [latex]\scriptsize DC=15\ \text{km}[/latex]. [latex]\scriptsize D\hat{A}B={{102}^\circ}[/latex], [latex]\scriptsize {{\hat{D}}_{2}}={{41}^\circ}[/latex] and [latex]\scriptsize A\hat{D}C={{75}^\circ}[/latex]
   
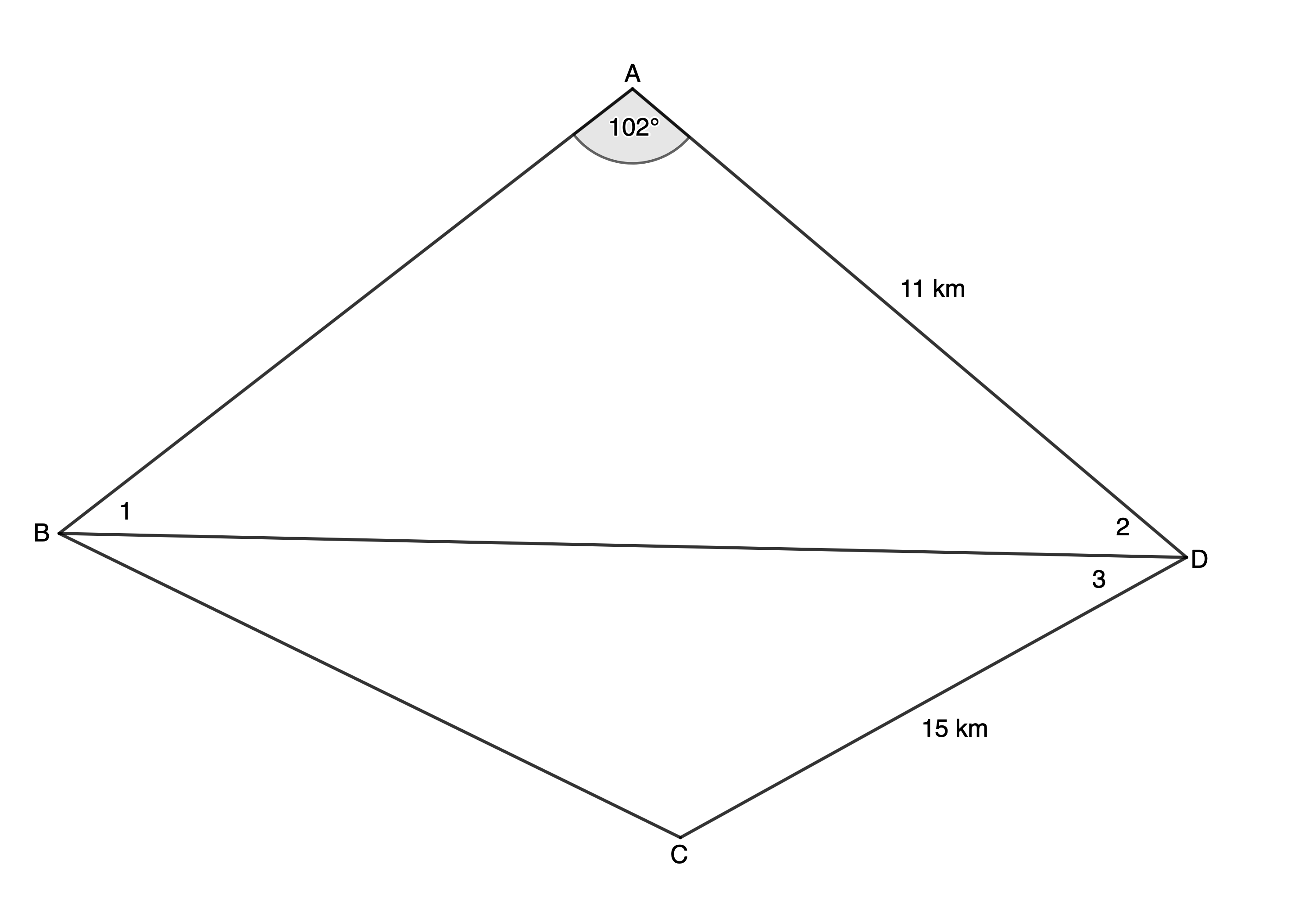
   1. Calculate [latex]\scriptsize {{\hat{B}}_{1}}[/latex].
   2. Calculate the length of the fence.
   3. If [latex]\scriptsize C={{130}^\circ}[/latex], calculate the length of [latex]\scriptsize BC[/latex].

Question 3 is adapted from NC(V) Mathematics Level 3 Paper 2 March 2011 question 1.6

3. In the figure below, [latex]\scriptsize KLMN[/latex] is a quadrilateral with [latex]\scriptsize \hat{M}={{125}^\circ}[/latex], [latex]\scriptsize N\hat{L}M={{28}^\circ}[/latex], [latex]\scriptsize K\hat{N}L={{90}^\circ}[/latex], [latex]\scriptsize MN=5\ \text{cm}[/latex] and [latex]\scriptsize KL=12\ \text{cm}[/latex].
   
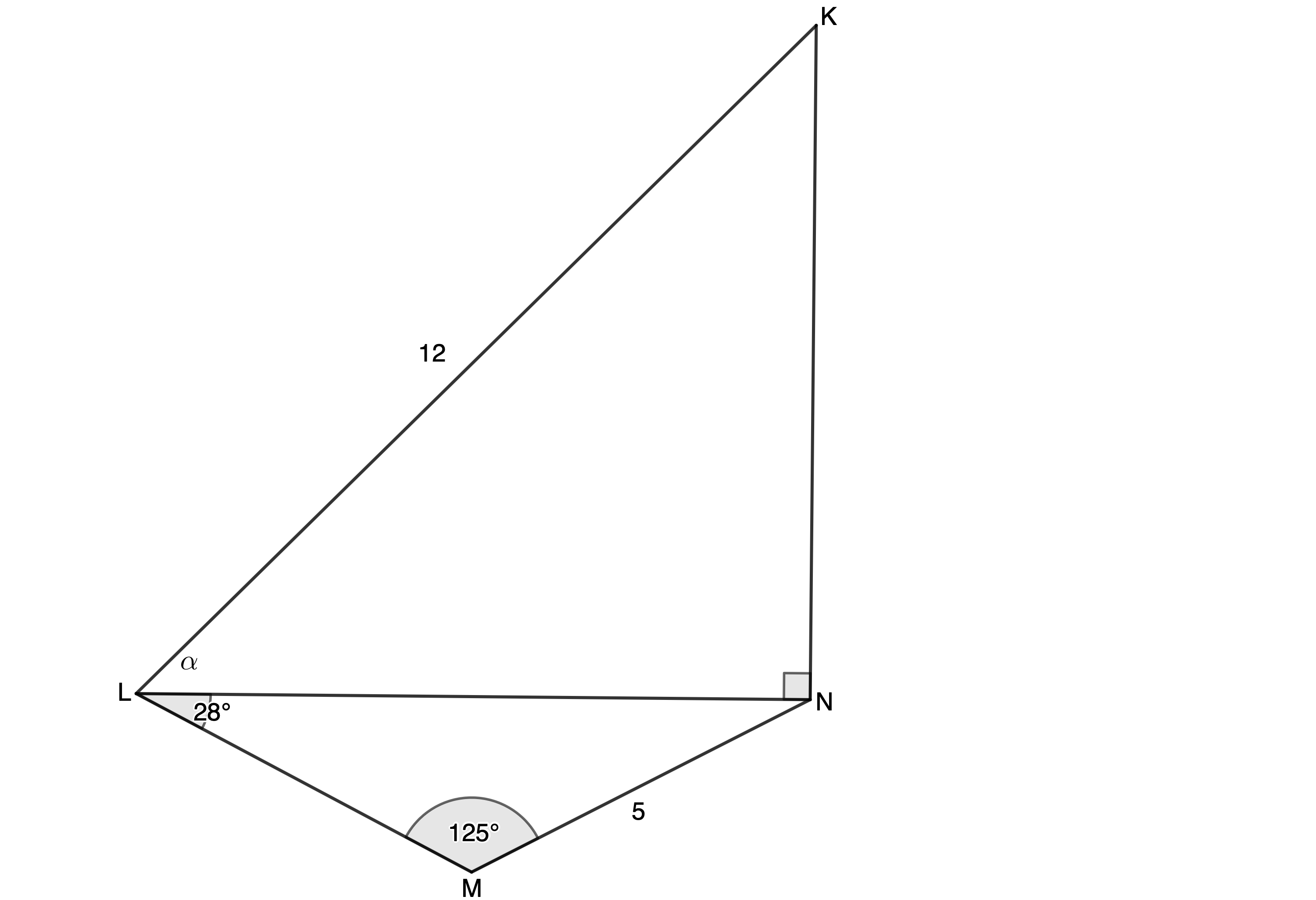
   1. Prove that [latex]\scriptsize LN=8.7\ \text{cm}[/latex] (to one decimal place).
   2. Determine the size of [latex]\scriptsize \alpha[/latex].
   3. Calculate the area of [latex]\scriptsize \Delta LMN[/latex].

The full solutions are at the end of the unit.

Unit 6: Solutions

Exercise 6.1

1. .
   1. First draw a sketch of the given information. Because we are given two angles and a side, we do not need to worry about the ambiguous case.
      
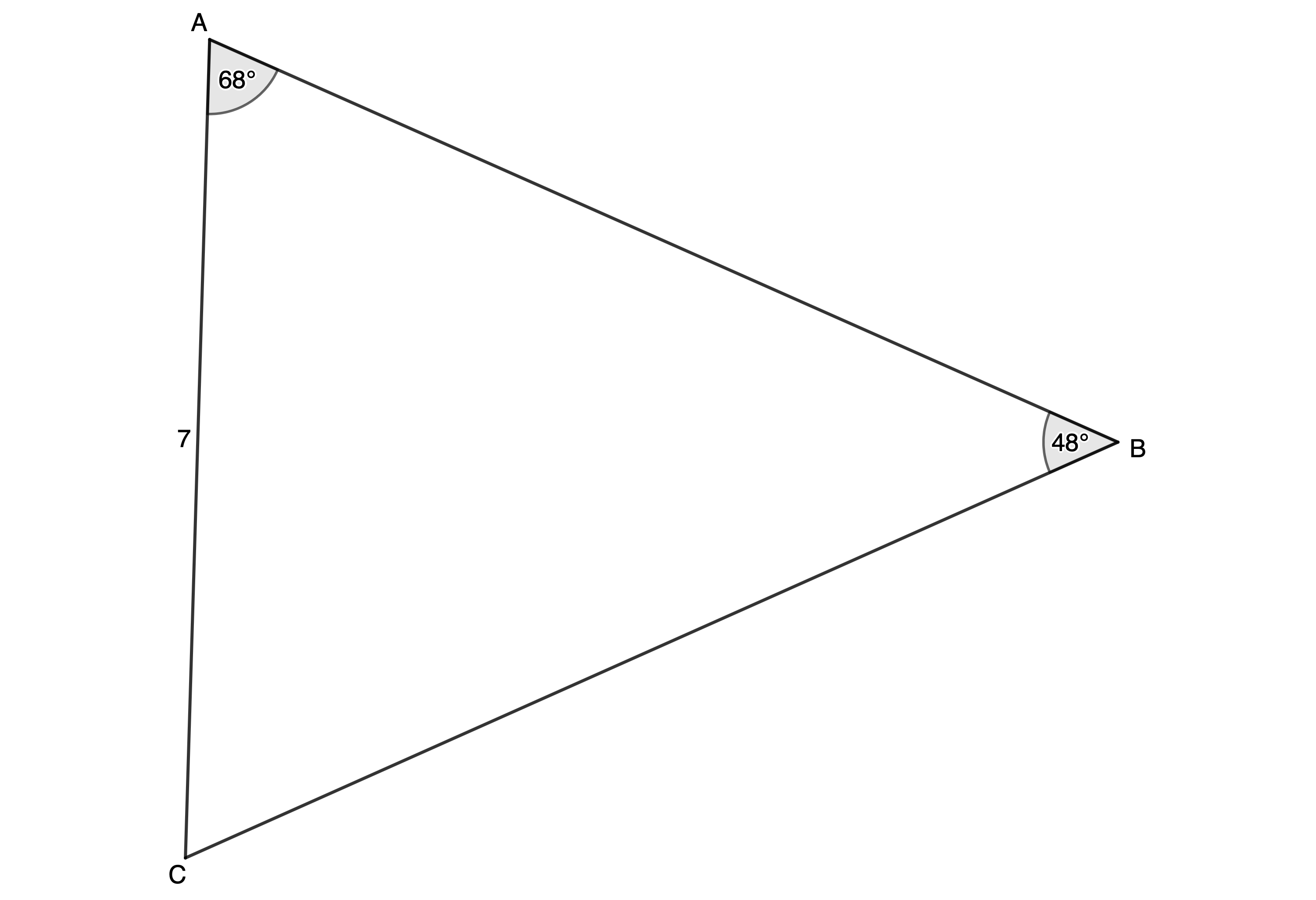
      [latex]\scriptsize \hat{C}={{180}^\circ}-{{68}^\circ}-{{48}^\circ}={{64}^\circ}[/latex] (angles in a triangle are supplementary)
      [latex]\scriptsize \begin{align*}\displaystyle \frac{a}{{\sin A}} & =\displaystyle \frac{b}{{\sin B}}\\\therefore \displaystyle \frac{a}{{\sin {{{68}}^\circ}}} & =\displaystyle \frac{7}{{\sin {{{48}}^\circ}}}\\\therefore a & =\displaystyle \frac{{7\sin {{{68}}^\circ}}}{{\sin {{{48}}^\circ}}}\\ & =8.73\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}\displaystyle \frac{c}{{\sin C}} & =\displaystyle \frac{b}{{\sin B}}\\\therefore \displaystyle \frac{c}{{\sin {{{64}}^\circ}}} & =\displaystyle \frac{7}{{\sin {{{48}}^\circ}}}\\\therefore c & =\displaystyle \frac{{7\sin {{{64}}^\circ}}}{{\sin {{{48}}^\circ}}}\\ & =8.47\end{align*}[/latex]
   2. First draw a sketch of the given information. Because we are given two angles and a side, we do not need to worry about the ambiguous case.
      
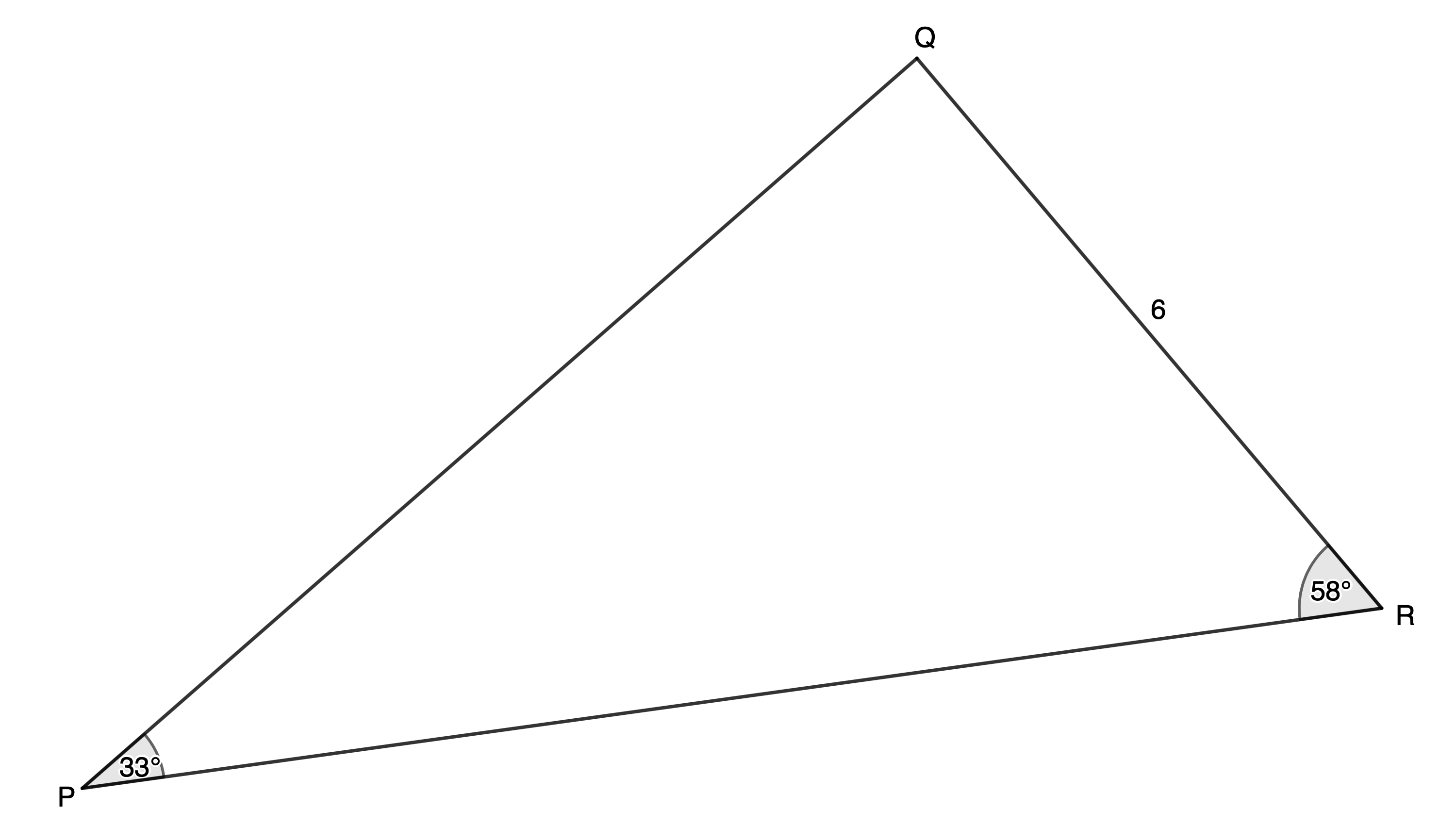
      [latex]\scriptsize \hat{Q}={{180}^\circ}-{{58}^\circ}-{{33}^\circ}={{89}^\circ}[/latex] (angles in a triangle are supplementary)
      [latex]\scriptsize \begin{align*}\displaystyle \frac{q}{{\sin Q}} & =\displaystyle \frac{p}{{\sin P}}\\\therefore \displaystyle \frac{q}{{\sin {{{89}}^\circ}}} & =\displaystyle \frac{6}{{\sin {{{33}}^\circ}}}\\\therefore q & =\displaystyle \frac{{6\sin {{{89}}^\circ}}}{{\sin {{{33}}^\circ}}}\\ & =11.01\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}\displaystyle \frac{r}{{\sin R}} & =\displaystyle \frac{p}{{\sin P}}\\\therefore \displaystyle \frac{r}{{\sin {{{58}}^\circ}}} & =\displaystyle \frac{6}{{\sin {{{33}}^\circ}}}\\\therefore r & =\displaystyle \frac{{6\sin {{{58}}^\circ}}}{{\sin {{{33}}^\circ}}}\\ & =9.34\end{align*}[/latex]
   3. First draw a sketch of the given information. Because we are given two sides and an angle, we need to check for the ambiguous case. Because the side opposite the given angle is the shorter, we have the ambiguous case. Sketch both cases.
      
      
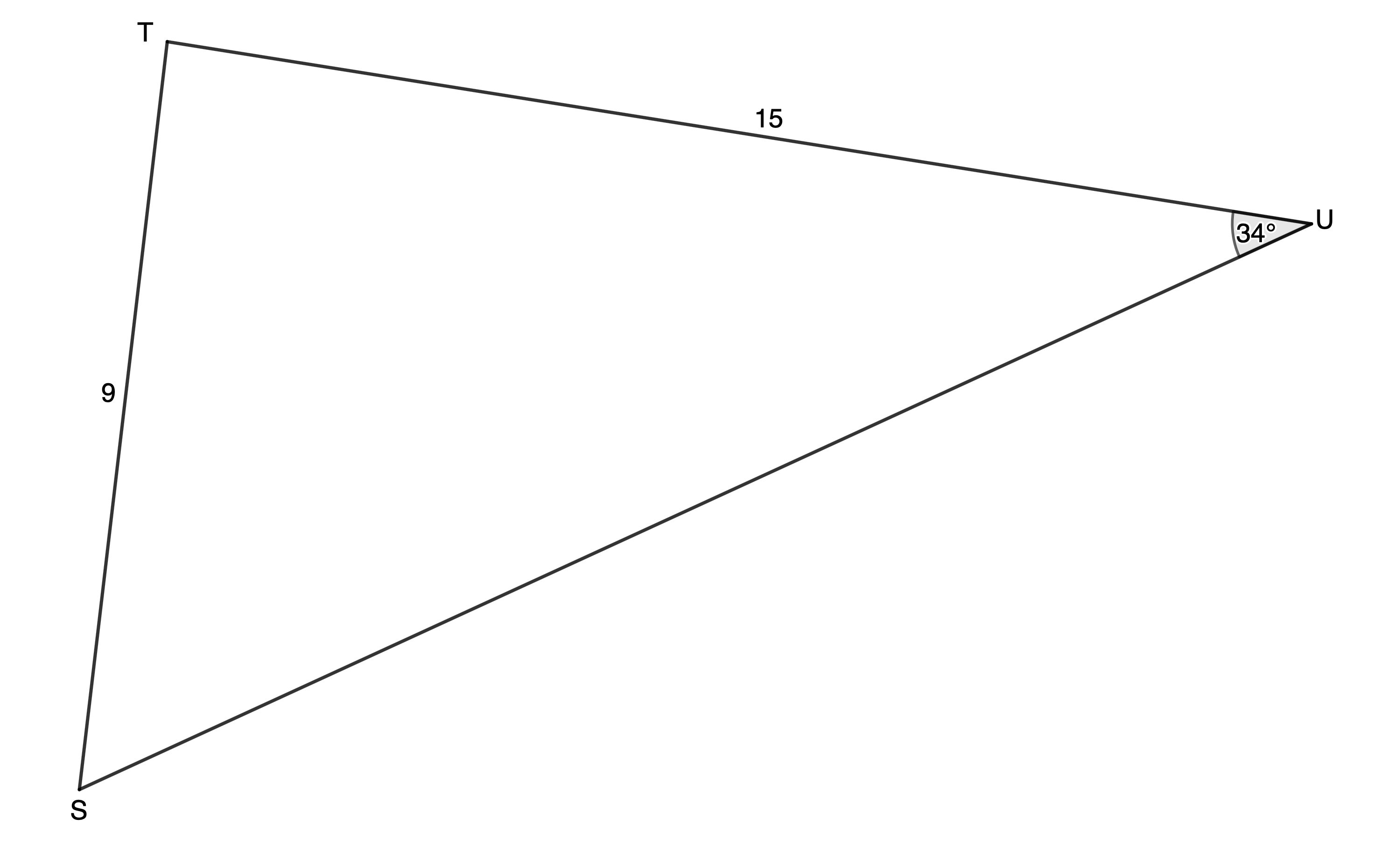
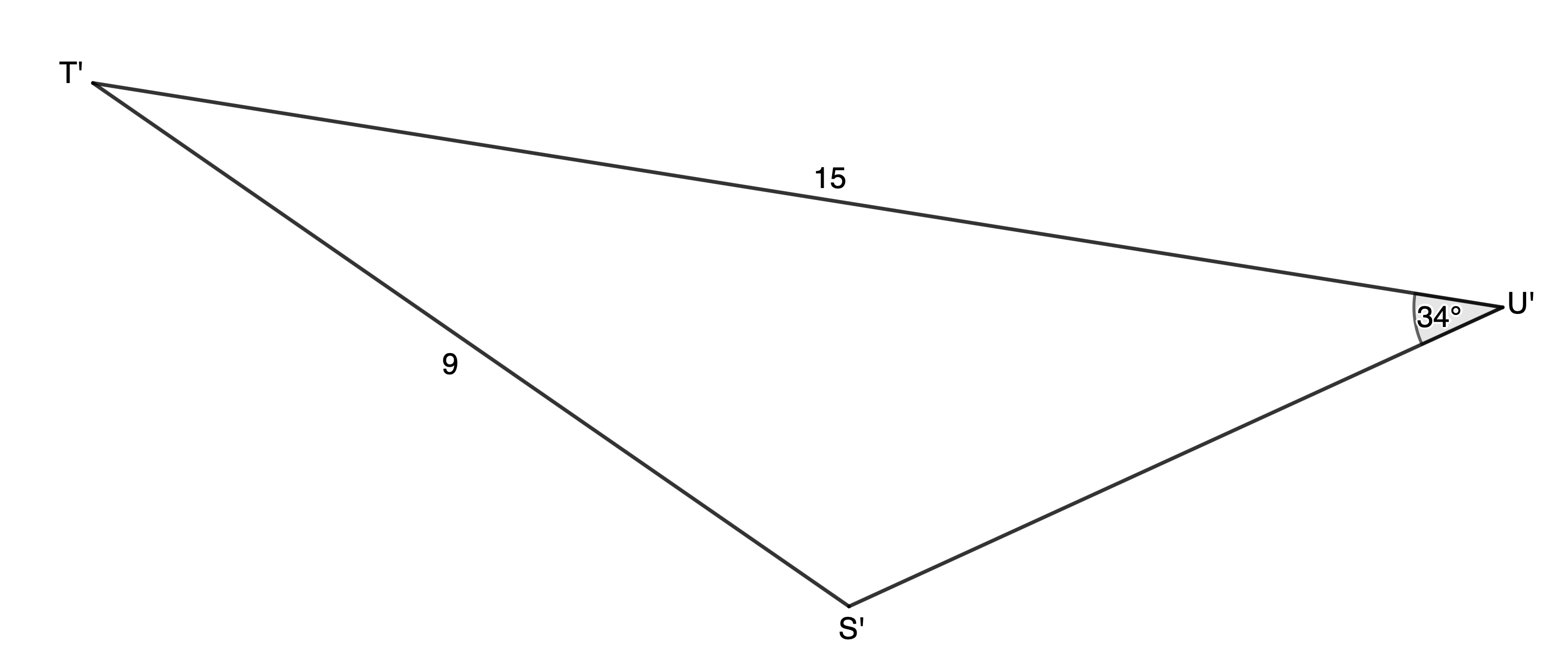
      In [latex]\scriptsize \Delta STU[/latex]:
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin S}}{s} & =\displaystyle \frac{{\sin U}}{u}\\\therefore \displaystyle \frac{{\sin S}}{{15}} & =\displaystyle \frac{{\sin {{{34}}^\circ}}}{9}\\\therefore \sin S & =\displaystyle \frac{{15\sin {{{34}}^\circ}}}{9}\\\therefore \hat{S} & ={{68.75}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \hat{T}={{180}^\circ}-{{68.75}^\circ}-{{34}^\circ}={{77.25}^\circ}[/latex] (angles in a triangle are supplementary)
      [latex]\scriptsize \begin{align*}\displaystyle \frac{t}{{\sin T}} & =\displaystyle \frac{u}{{\sin U}}\\\therefore \displaystyle \frac{t}{{\sin {{{77.25}}^\circ}}} & =\displaystyle \frac{9}{{\sin {{{34}}^\circ}}}\\\therefore t & =\displaystyle \frac{{9\sin {{{77.25}}^\circ}}}{{\sin {{{34}}^\circ}}}\\ & =15.70\end{align*}[/latex]
      In [latex]\scriptsize \Delta S'T'U'[/latex]:
      [latex]\scriptsize \hat{S}={{180}^\circ}-{{68.75}^\circ}={{111.25}^\circ}[/latex]
      [latex]\scriptsize \hat{T}={{180}^\circ}-{{111.25}^\circ}-{{34}^\circ}={{34.75}^\circ}[/latex] (angles in a triangle are supplementary)
      [latex]\scriptsize \begin{align*}\displaystyle \frac{t}{{\sin T}} & =\displaystyle \frac{u}{{\sin U}}\\\therefore \displaystyle \frac{t}{{\sin {{{34.75}}^\circ}}} & =\displaystyle \frac{9}{{\sin {{{34}}^\circ}}}\\\therefore t & =\displaystyle \frac{{9\sin {{{34.75}}^\circ}}}{{\sin {{{34}}^\circ}}}\\ & =9.17\end{align*}[/latex]
   4. First draw a sketch of the given information. Because we are given two sides and an angle, we need to check for the ambiguous case. Because the side opposite the given angle is the longer, we do not have the ambiguous case.
      
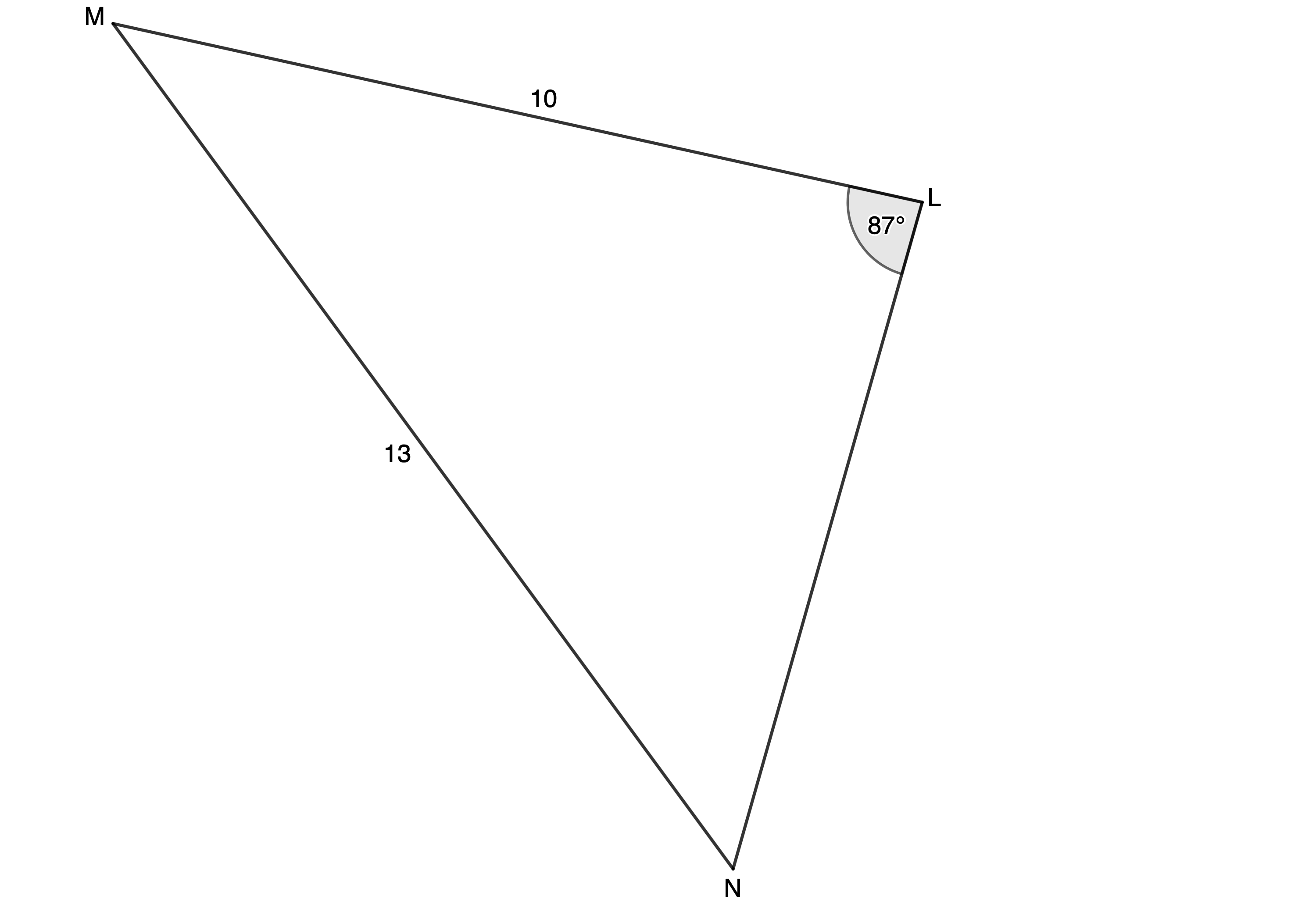
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin N}}{n} & =\displaystyle \frac{{\sin L}}{l}\\\therefore \displaystyle \frac{{\sin N}}{{10}} & =\displaystyle \frac{{\sin {{{87}}^\circ}}}{{13}}\\\therefore \sin N & =\displaystyle \frac{{10\sin {{{87}}^\circ}}}{{13}}\\\therefore \hat{N} & ={{50.19}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \hat{M}={{180}^\circ}-{{87}^\circ}-{{50.19}^\circ}={{42.81}^\circ}[/latex] (angles in a triangle are supplementary)
      [latex]\scriptsize \begin{align*}\displaystyle \frac{m}{{\sin M}} & =\displaystyle \frac{l}{{\sin L}}\\\therefore \displaystyle \frac{m}{{\sin {{{42.81}}^\circ}}} & =\displaystyle \frac{{13}}{{\sin {{{87}}^\circ}}}\\\therefore m & =\displaystyle \frac{{13\sin {{{42.81}}^\circ}}}{{\sin {{{87}}^\circ}}}\\ & =8.85\end{align*}[/latex]
2. .
   1. In [latex]\scriptsize \Delta ACD[/latex]:
      [latex]\scriptsize x={{180}^\circ}-{{90}^\circ}-({{20}^\circ}+{{25}^\circ})={{45}^\circ}[/latex] (angles in a triangle are supplementary)
   2. In [latex]\scriptsize \Delta BCD[/latex]:
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{DB}}{{\sin C}} & =\displaystyle \frac{{BC}}{{\sin B\hat{D}C}}\\\therefore \displaystyle \frac{{DB}}{{\sin {{{90}}^\circ}}} & =\displaystyle \frac{{10.5}}{{\sin {{{25}}^\circ}}}\\\therefore DB & =\displaystyle \frac{{10.5\sin {{{90}}^\circ}}}{{\sin {{{25}}^\circ}}}\\ & =24.85\ \text{cm}\end{align*}[/latex]
   3. In [latex]\scriptsize \Delta ABD[/latex]:
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{AB}}{{\sin A\hat{D}B}} & =\displaystyle \frac{{DB}}{{\sin x}}\\\therefore \displaystyle \frac{{AB}}{{\sin {{{20}}^\circ}}} & =\displaystyle \frac{{24.85}}{{\sin {{{45}}^\circ}}}\\\therefore AB & =\displaystyle \frac{{24.85\sin {{{20}}^\circ}}}{{\sin {{{45}}^\circ}}}\\ & =12.02\ \text{cm}\end{align*}[/latex]

Back to Exercise 6.1

Unit 6: Assessment

1. .
   1. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{AH}}{{\sin B}} & =\displaystyle \frac{{AB}}{{\sin A\hat{H}B}}\\\therefore \displaystyle \frac{{AH}}{{\sin {{{23}}^\circ}}} & =\displaystyle \frac{{10}}{{\sin {{{90}}^\circ}}}\\\therefore AH & =\displaystyle \frac{{10\sin {{{23}}^\circ}}}{{\sin {{{90}}^\circ}}}\\ & =3.91\ \text{cm}\end{align*}[/latex]
   2. [latex]\scriptsize B\hat{A}D={{90}^\circ}[/latex] (given)
      [latex]\scriptsize \hat{D}={{180}^\circ}-\hat{B}-B\hat{A}D={{180}^\circ}-{{23}^\circ}-{{90}^\circ}={{67}^\circ}[/latex] (angles in a triangle are supplementary)
      [latex]\scriptsize D\hat{A}H={{180}^\circ}-A\hat{H}D-\hat{D}={{180}^\circ}-{{90}^\circ}-{{67}^\circ}={{23}^\circ}[/latex] (angles in a triangle are supplementary)
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{HD}}{{\sin D\hat{A}H}} & =\displaystyle \frac{{AH}}{{\sin \hat{D}}}\\\therefore \displaystyle \frac{{HD}}{{\sin {{{23}}^\circ}}} & =\displaystyle \frac{{3.91}}{{\sin {{{67}}^\circ}}}\\\therefore HD & =\displaystyle \frac{{3.91\sin {{{23}}^\circ}}}{{\sin {{{67}}^\circ}}}\\ & =1.66\ \text{cm}\end{align*}[/latex]
2. .
   1. [latex]\scriptsize {{\hat{B}}_{1}}={{180}^\circ}-\hat{A}-{{\hat{D}}_{2}}={{180}^\circ}-{{102}^\circ}-{{41}^\circ}={{37}^\circ}[/latex] (angles in a triangle are supplementary)
   2. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{BD}}{{\sin A}} & =\displaystyle \frac{{AD}}{{\sin {{B}_{1}}}}\\\therefore \displaystyle \frac{{BD}}{{\sin {{{102}}^\circ}}} & =\displaystyle \frac{{11}}{{\sin {{{37}}^\circ}}}\\\therefore BD & =\displaystyle \frac{{11\sin {{{102}}^\circ}}}{{\sin {{{37}}^\circ}}}\\ & =17.88\ \text{km}\end{align*}[/latex]
      c. [latex]\scriptsize A\hat{D}C={{75}^\circ}={{\hat{D}}_{2}}+{{\hat{D}}_{3}}[/latex] (given)
      [latex]\scriptsize \therefore {{D}_{3}}={{75}^\circ}-{{41}^\circ}={{34}^\circ}[/latex]
      [latex]\scriptsize \hat{C}={{130}^\circ}[/latex] (given)
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{BC}}{{\sin {{{\hat{D}}}_{3}}}} & =\displaystyle \frac{{BD}}{{\sin \hat{C}}}\\\therefore \displaystyle \frac{{BC}}{{\sin {{{34}}^\circ}}} & =\displaystyle \frac{{17.88}}{{\sin {{{130}}^\circ}}}\\\therefore BC & =\displaystyle \frac{{17.88\sin {{{34}}^\circ}}}{{\sin {{{130}}^\circ}}}\\ & =13.05\ \text{km}\end{align*}[/latex]
3. .
   1. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{LN}}{{\sin M}} & =\displaystyle \frac{{MN}}{{\sin L}}\\\therefore \displaystyle \frac{{LN}}{{\sin {{{125}}^\circ}}} & =\displaystyle \frac{5}{{\sin {{{28}}^\circ}}}\\\therefore LN & =\displaystyle \frac{{5\sin {{{125}}^\circ}}}{{\sin {{{28}}^\circ}}}\\=8.7\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin K}}{{LN}} & =\displaystyle \frac{{\sin K\hat{N}L}}{{KL}}\\\therefore \displaystyle \frac{{\sin K}}{{8.7}} & =\displaystyle \frac{{\sin {{{90}}^\circ}}}{{12}}\\\therefore \sin K & =\displaystyle \frac{{8.7\sin {{{90}}^\circ}}}{{12}}\\\therefore K & ={{46.47}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \alpha ={{180}^\circ}-{{90}^\circ}-{{46.47}^\circ}={{43.53}^\circ}[/latex] (angles in triangle are supplementary)
   3. [latex]\scriptsize L\hat{N}M={{180}^\circ}-{{28}^\circ}-{{125}^\circ}={{27}^\circ}[/latex] (angles in triangle are supplementary)
      [latex]\scriptsize \begin{align*}\text{Area }\Delta LMN&=\displaystyle \frac{1}{2}\times LN\times MN\times \sin L\hat{N}M\\&=\displaystyle \frac{1}{2}\times 8.7\times 5\times \sin {{27}^\circ}\\&=9.87\ {{\text{u}}^{2}}\end{align*}[/latex]

Back to Unit 6: Assessment