Functions and algebra: Solve algebraic equations and inequalities
Unit 5: Solve quadratic inequalities
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Find the critical values.
- Solve quadratic inequalities using the table and graphical methods.
- Represent the solution using set builder notation, interval notation and on a number line.
What you should know
Before you start this unit, make sure you can:
- Solve linear inequalities. Refer to level 2 subject outcome 2.3 unit 3 if you need help with this.
- Represent inequalities using set interval notation, set builder notation and on a number line. Refer to level 2 subject outcome 2.3 unit 3 if you need help with this.
Here is a short self-assessment to make sure you have the basic skills you need to proceed with this unit.
Solve for [latex]\scriptsize x[/latex] and show your answer as indicated:
- [latex]\scriptsize 2-3x\le 3-5x[/latex] (show your answer on a number line)
- [latex]\scriptsize \displaystyle \frac{{7x+3}}{4} \lt 4(2x-7)[/latex] (show your answer using interval and set builder notation)
Solutions
- .
[latex]\scriptsize \begin{align*}2-3x&\le 3-5x\\ \therefore -3x & \le 1-5x&& \text{Subtract }2\text{ from both sides of the inequality}\\ \therefore 2x & \le 1 &&\text{Add }5x\text{ to both sides of the inequality}\\ \therefore x & \le \displaystyle \frac{1}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{7x+3}}{4} &\lt 4(2x-7)\\ \therefore 7x+3 & \lt 16(2x-7)\\ \therefore 7x+3 & \lt 32x-112\\ \therefore -25x & \lt -115 &&\text{Remember, we need to change the direction of the inequality sign}\\ &&& \text{when multipling by a negative number}\\ \therefore x & \gt \displaystyle \frac{{115}}{{25}}\\ \therefore x & \gt \displaystyle \frac{{23}}{5}\end{align*}[/latex]Interval notation: [latex]\scriptsize x\in (\displaystyle \frac{{23}}{5},\infty )[/latex]
Set builder notation: [latex]\scriptsize \{x|x\in \mathbb{R},x \gt \displaystyle \frac{{23}}{5}\}[/latex]
Introduction
We learnt how to solve linear inequalities in level 2 subject outcome 2.3 unit 3. We saw that solving for the unknown in an inequality is very similar to solving for an unknown in an equation.
In this unit, we are going to learn how to solve quadratic inequalities. Again, the basic techniques for solving inequalities and equations are very similar. The biggest difference is still the fact that we have to flip the inequality sign around if we multiply both sides of an inequality by a negative number.
Solve simple quadratic inequalities
If [latex]\scriptsize a{{x}^{2}}+bx+c=0[/latex] is the standard form of a quadratic equation, then it stands to reason that the following are the standard forms of a quadratic inequality:
- [latex]\scriptsize a{{x}^{2}}+bx+c\ge 0[/latex]
- [latex]\scriptsize a{{x}^{2}}+bx+c \gt 0[/latex]
- [latex]\scriptsize a{{x}^{2}}+bx+c\le 0[/latex]
- [latex]\scriptsize a{{x}^{2}}+bx+c \lt 0[/latex]
We know that quadratic equations give us two solutions or roots. But how does this translate into the solutions to quadratic inequalities? Are there always two ranges?
A useful way to think about the solutions to a quadratic inequality is to think about where the graph of the quadratic equation lies in relation to the x-axis. Think about the quadratic function [latex]\scriptsize f(x)={{x}^{2}}+3x-4[/latex] (see figure 1).
We know that the solution to [latex]\scriptsize {{x}^{2}}+3x-4=0[/latex] gives us the x-intercepts (see Figure 1). This is where the function [latex]\scriptsize f(x)=0[/latex]. The x-values of the x-intercepts are the roots. They are the specific values that make the function value zero.
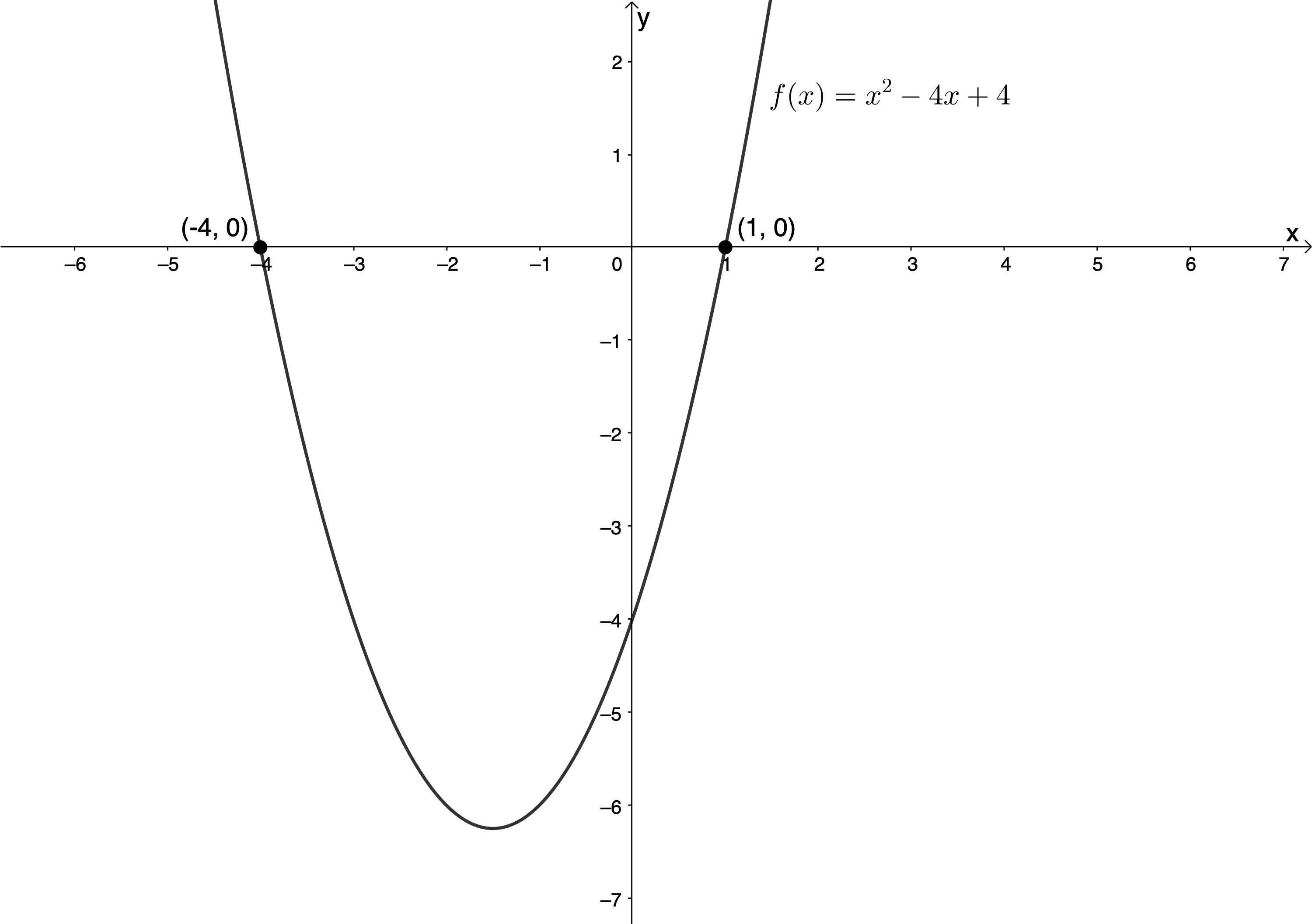
Now, if we solve the quadratic inequality of [latex]\scriptsize {{x}^{2}}+3x-4\le 0[/latex], what x-values do you think will satisfy this inequality? What x-values will make [latex]\scriptsize f(x)\le 0[/latex]?
You should be able to see that any value for [latex]\scriptsize x[/latex] that lies between the x-intercepts will result in [latex]\scriptsize f(x)\le 0[/latex] (that part of the graph of the function below the x-axis) (see Figure 2).
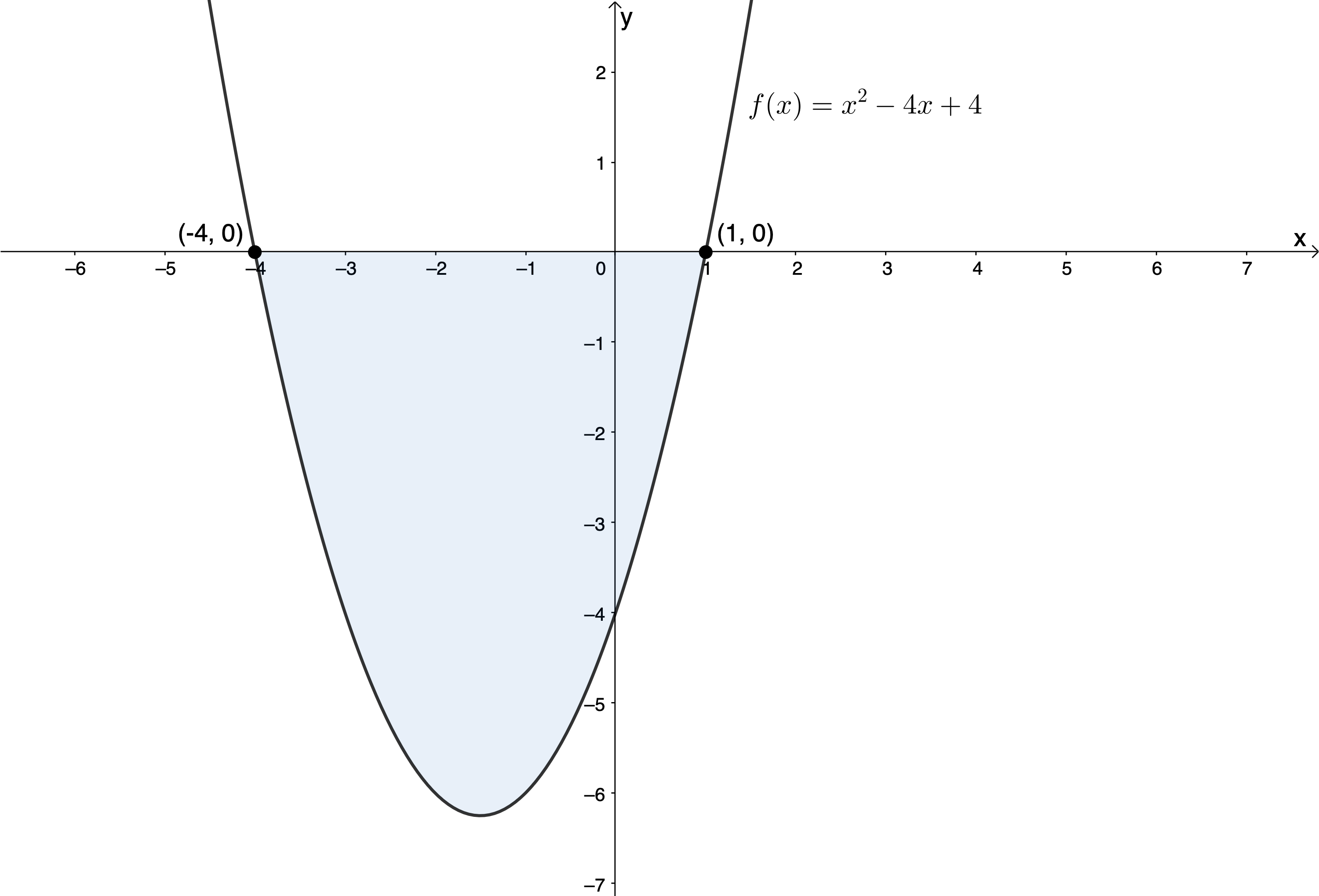
We can present the solution to the quadratic inequality [latex]\scriptsize {{x}^{2}}+3x-4\le 0[/latex] on a number line (see Figure 3).

We can also write the solution as [latex]\scriptsize x\in [-4,1][/latex] (interval notation) or [latex]\scriptsize \{x|x\in \mathbb{R},-4\le x\le 1\}[/latex] (set builder notation). Note that because we are also interested in where the function is equal to zero, we include the roots in our solution.
Now, what do you think the solution to the quadratic inequality [latex]\scriptsize {{x}^{2}}+3x-4 \gt 0[/latex] will be? Note that we are interested in where [latex]\scriptsize f(x) \gt 0[/latex] (in other words where the graph of the function is above the x-axis) and that we need to exclude the values where [latex]\scriptsize f(x)=0[/latex] (in other words the roots).
Figure 4 shows the solution to [latex]\scriptsize {{x}^{2}}+3x-4 \gt 0[/latex] graphically. We can see that we need x-values to the left of [latex]\scriptsize -4[/latex] and to the right of [latex]\scriptsize 1[/latex].
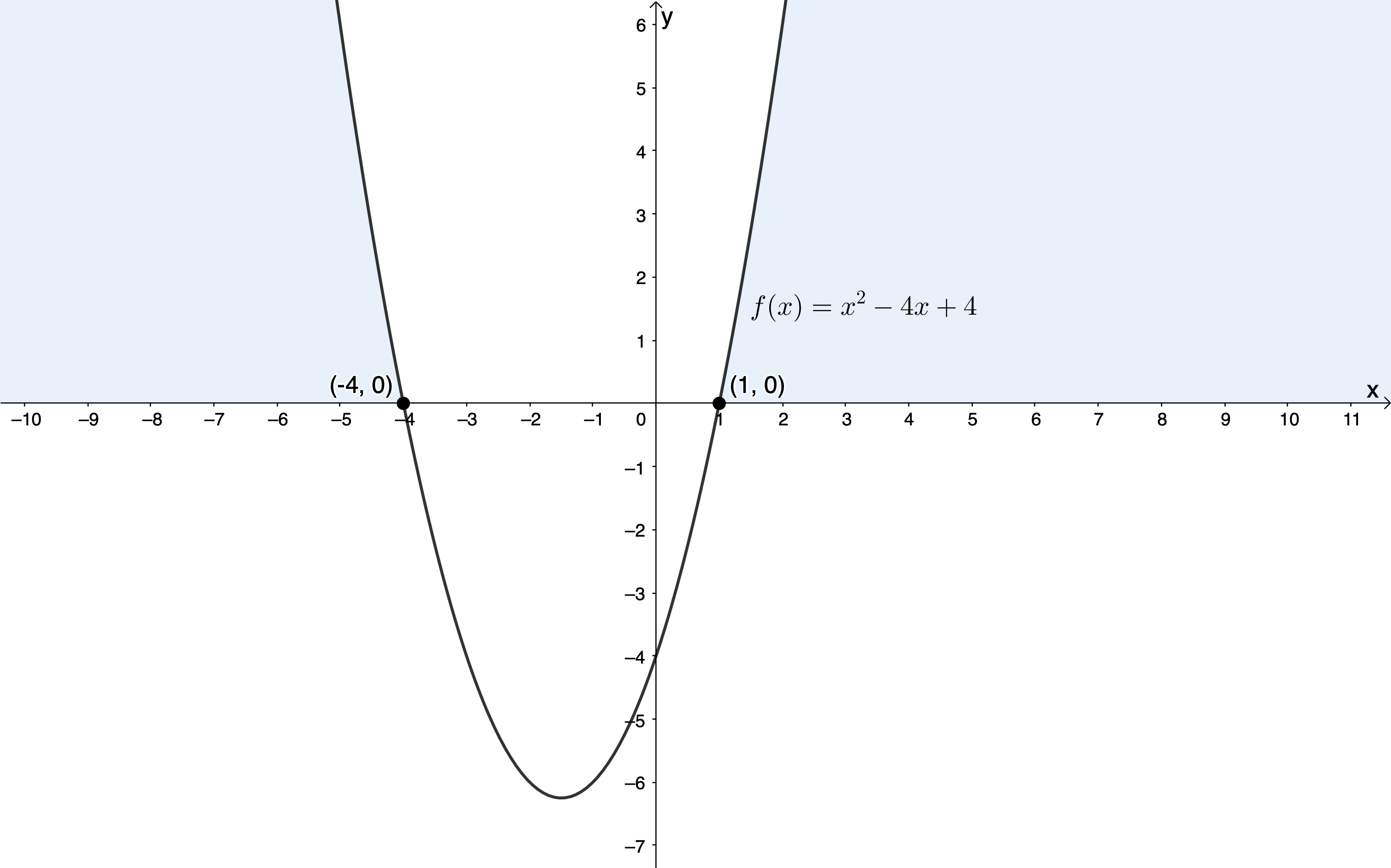
We can represent this on a number line (see Figure 5), using interval notation [latex]\scriptsize x\in (-\infty ,-4)\bigcup (1,\infty )[/latex] or set builder notation [latex]\scriptsize \{x|x\in \mathbb{R},x \lt -4,x \gt 1\}[/latex].
When representing the solution on a number line, we use a closed dot to represent values that are included (i.e. [latex]\scriptsize \le \text{ and }\ge \text{ }[/latex] or [latex]\scriptsize [\text{ and }\!\!]\!\!\text{ }[/latex]). We use an open dot to represent values that are not included (i.e. or [latex]\scriptsize (\text{ and )}[/latex]).
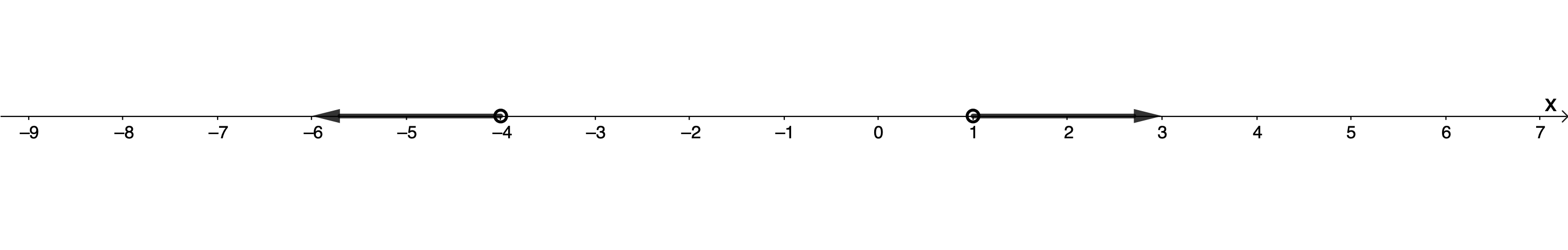
Take note!
The [latex]\scriptsize \bigcup[/latex] symbol in [latex]\scriptsize x\in (-\infty ,-4)\bigcup (1,\infty )[/latex] is called Union and it lets us combine different intervals of values together into a single solution set.
Sketching the graph of the quadratic function each time we want to solve a quadratic inequality would be effective but not very efficient. Instead, we use a simplified representation of a table of values to figure out where the quadratic function is positive or negative and then build our solution from here. Take a look at Example 5.1 to see how this works.
Example 5.1
Solve for [latex]\scriptsize x[/latex] in [latex]\scriptsize {{x}^{2}}+3x-4\ge 0[/latex].
Solution
Notice that we are dealing with the same quadratic as above, so feel free to have a look at the figures above as you work through this solution.
Step 1: Get the inequality into standard form
The first step is always to get the quadratic inequality into standard form. Remember to flip the direction of the inequality sign if you ever multiply through by a negative number. Our inequality is already in standard form.
[latex]\scriptsize {{x}^{2}}+3x-4\ge 0[/latex]
Step 2: Determine the critical values
The critical values are the roots of the corresponding quadratic equation. Remember these are the x-values where the function is zero as it goes from being positive to negative or negative to positive.
[latex]\scriptsize \begin{align*}{{x}^{2}}+3x-4 & \ge 0\\\therefore (x+4)(x-1) & \ge 0\end{align*}[/latex]
Our critical values are, therefore, [latex]\scriptsize x=-4[/latex] and [latex]\scriptsize x=1[/latex].
Note
Almost always, the quadratic inequalities that you will be expected to solve will factorise easily. It would be a very nasty question that expects you to find the critical values by using the quadratic formula. If you find that your quadratic expression does not factorise, first go back to check your work before using the quadratic formula.
Step 3: Complete a table of signs
Create a table like this:
| [latex]\scriptsize x \lt -4[/latex] | [latex]\scriptsize x=-4[/latex] | [latex]\scriptsize -4 \lt x \lt 1[/latex] | [latex]\scriptsize x=1[/latex] | [latex]\scriptsize x \gt 1[/latex] | |
| [latex]\scriptsize (x+4)(x-1)[/latex] |
We know that each factor will be zero at its respective critical value and therefore, the whole quadratic expression will be zero at these values. So, fill this into your table.
| [latex]\scriptsize x \lt -4[/latex] | [latex]\scriptsize x=-4[/latex] | [latex]\scriptsize -4 \lt x \lt 1[/latex] | [latex]\scriptsize x=1[/latex] | [latex]\scriptsize x \gt 1[/latex] | |
| [latex]\scriptsize (x+4)(x-1)[/latex] | [latex]\scriptsize 0[/latex] | [latex]\scriptsize 0[/latex] |
Next, you need to determine whether the quadratic expression is positive or negative on either side of each critical value. Start by picking any value less than [latex]\scriptsize -4[/latex], say [latex]\scriptsize -5[/latex].
[latex]\scriptsize (x+4)=-5+4=-1 \lt 0[/latex] and [latex]\scriptsize (x-1)=-5-1=-6 \lt 0[/latex]. Therefore, the overall product will be positive. Fill this into your table.
| [latex]\scriptsize x \lt -4[/latex] | [latex]\scriptsize x=-4[/latex] | [latex]\scriptsize -4 \lt x \lt 1[/latex] | [latex]\scriptsize x=1[/latex] | [latex]\scriptsize x \gt 1[/latex] | |
| [latex]\scriptsize (x+4)(x-1)[/latex] | [latex]\scriptsize +[/latex] | [latex]\scriptsize 0[/latex] | [latex]\scriptsize 0[/latex] |
Complete the rest of the table by choosing the appropriate values and testing to see whether the product of the factors is positive or negative. The final table will look like this:
| [latex]\scriptsize x \lt -4[/latex] | [latex]\scriptsize x=-4[/latex] | [latex]\scriptsize -4 \lt x \lt 1[/latex] | [latex]\scriptsize x=1[/latex] | [latex]\scriptsize x \gt 1[/latex] | |
| [latex]\scriptsize (x+4)(x-1)[/latex] | [latex]\scriptsize +[/latex] | [latex]\scriptsize 0[/latex] | [latex]\scriptsize -[/latex] | [latex]\scriptsize 0[/latex] | [latex]\scriptsize +[/latex] |
Step 4: Read off the solution.
Now we can read off the solution to our inequality [latex]\scriptsize {{x}^{2}}+3x-4\ge 0[/latex]. We need all those ranges of values that are greater than or equal to zero. These are:
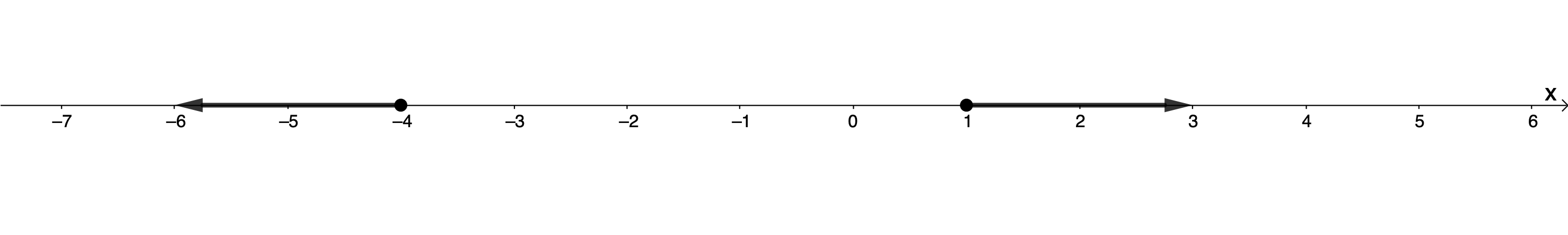
[latex]\scriptsize x\in (-\infty ,-4]\bigcup [1,\infty )[/latex]
[latex]\scriptsize \{x|x\in \mathbb{R},x\le -4,x\ge 1\}[/latex]
Example 5.2
Solve for [latex]\scriptsize x[/latex] in [latex]\scriptsize -{{x}^{2}}+6x\ge -7[/latex].
Solution
Step 1: Get the inequality into standard form
[latex]\scriptsize \begin{align*}-{{x}^{2}}+6x & \ge -7\\ \therefore -{{x}^{2}}+6x+7 & \ge 0\quad \text{Leave the inequality like this or multiply through by }-1\\ \therefore {{x}^{2}}-6x-7 & \le 0\quad \text{If you do multiply through by }-1\text{ remember to flip the inequality}\end{align*}[/latex]
Step 2: Determine the critical values
[latex]\scriptsize \begin{align*}{{x}^{2}}-6x-7 & \le 0\\ \therefore (x-7)(x+1) & \ge 0\end{align*}[/latex]
Our critical values are, therefore, [latex]\scriptsize x=-1[/latex] and [latex]\scriptsize x=7[/latex].
Step 3: Complete a table of signs
| [latex]\scriptsize x \lt -1[/latex] | [latex]\scriptsize x=-1[/latex] | [latex]\scriptsize -1 \lt x \lt 7[/latex] | [latex]\scriptsize x=7[/latex] | [latex]\scriptsize x \gt 7[/latex] | |
| [latex]\scriptsize (x-7)(x+1)[/latex] | [latex]\scriptsize +[/latex] | [latex]\scriptsize 0[/latex] | [latex]\scriptsize -[/latex] | [latex]\scriptsize 0[/latex] | [latex]\scriptsize +[/latex] |
Step 4: Read off the solution
[latex]\scriptsize {{x}^{2}}-6x-7 \le 0[/latex]. Therefore:

[latex]\scriptsize x\in [-1,7][/latex]
[latex]\scriptsize \{x|x\in \mathbb{R},-1\le x\le 7\}[/latex]
Exercise 5.1
Solve for [latex]\scriptsize x[/latex] in the following inequalities, representing your answer as indicated:
- [latex]\scriptsize {{x}^{2}}+2x-15 \lt 0[/latex] (represent your answer using set builder notation)
- [latex]\scriptsize 10{{x}^{2}}\le 31x-15[/latex] (represent your answer using interval notation)
- [latex]\scriptsize 9x(x+1) \gt 10[/latex] (represent your answer using interval notation)
- [latex]\scriptsize 5(2{{x}^{2}}-7) \lt 11x[/latex] (represent your answer using set builder notation)
- [latex]\scriptsize \displaystyle \frac{{40x-21}}{{{{x}^{2}}}}\ge 16[/latex] (represent your answer on a number line)
The full solutions are at the end of the unit.
Solve simple quadratic inequalities graphically
Let’s do a few more examples to show how to solve for [latex]\scriptsize x[/latex] graphically.
Example 5.3
Determine graphically for which values of [latex]\scriptsize x[/latex] [latex]\scriptsize f(x)\ge 0[/latex] if [latex]\scriptsize f(x)=-4{{x}^{2}}+4x+3[/latex].
Solution
The first thing to notice is that we need to solve for [latex]\scriptsize x[/latex] graphically, which means we have to draw a sketch of the function and interpret this sketch to come to the solution.
Step 1: Sketch the function
If you need help sketching quadratic functions like this refer to level 3 subject outcome 2.1 unit 1.
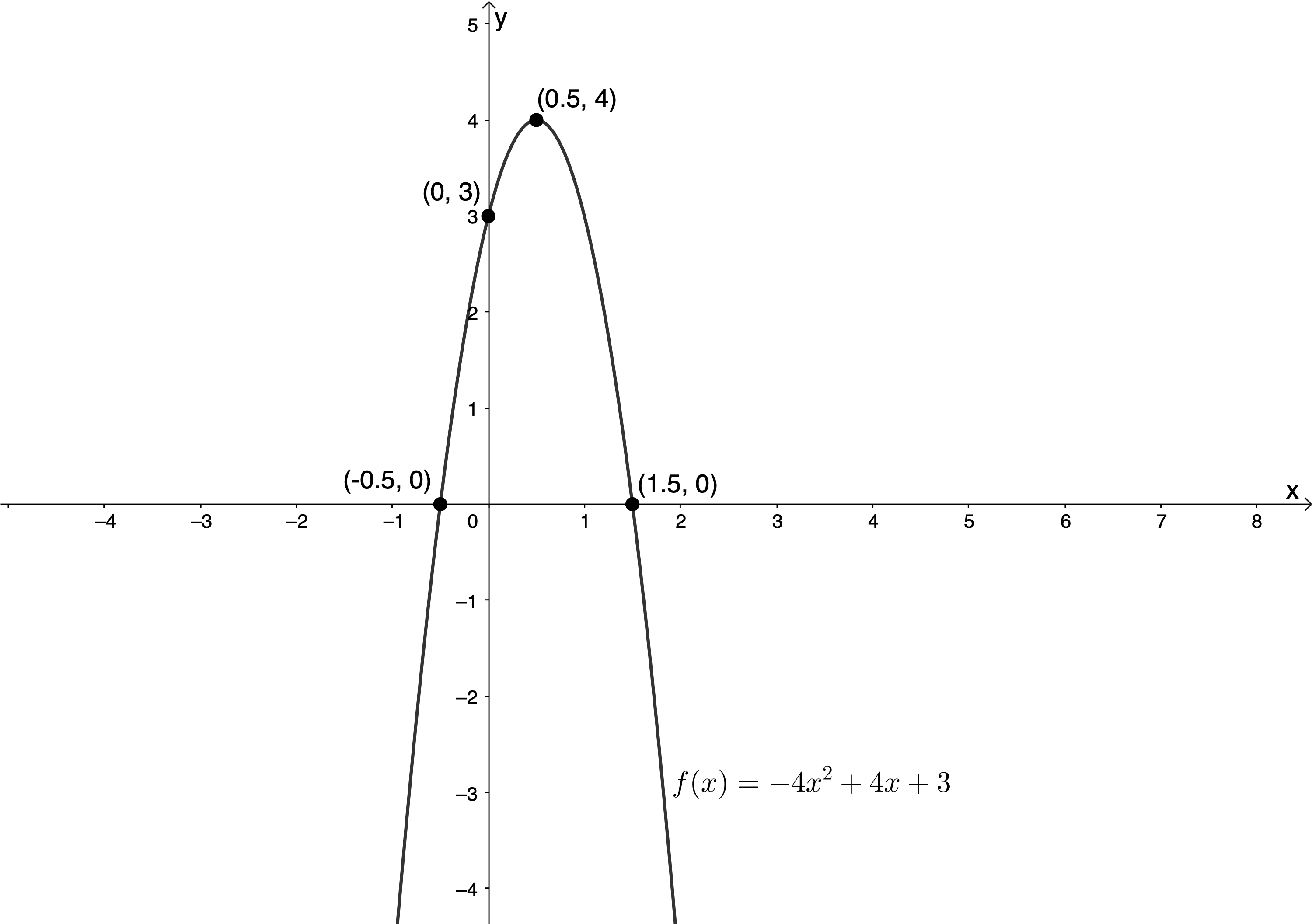
Step 2: Read off the solution
We were asked to find where [latex]\scriptsize f(x)\ge 0[/latex], in other words, where the function [latex]\scriptsize f[/latex] is above the x-axis. From the graph, we can see that [latex]\scriptsize f(x)\ge 0[/latex] between [latex]\scriptsize -\displaystyle \frac{1}{2}[/latex] and [latex]\scriptsize \displaystyle \frac{3}{2}[/latex]. Therefore, [latex]\scriptsize x\in [-\displaystyle \frac{1}{2},\displaystyle \frac{3}{2}][/latex] or [latex]\scriptsize \{x|x\in \mathbb{R}\text{,}-\displaystyle \frac{1}{2}\le x\le \displaystyle \frac{3}{2}\}[/latex]
There is something important we need to recognise about solving quadratic inequalities from Example 5.3. In this case, [latex]\scriptsize f(x)=-4{{x}^{2}}+4x+3[/latex] and we were asked where [latex]\scriptsize f(x)\ge 0[/latex] or above the x-axis. We can see that the graph has a maximum turning point because [latex]\scriptsize a \lt 0[/latex] and so the solution is as shown in Figure 6.
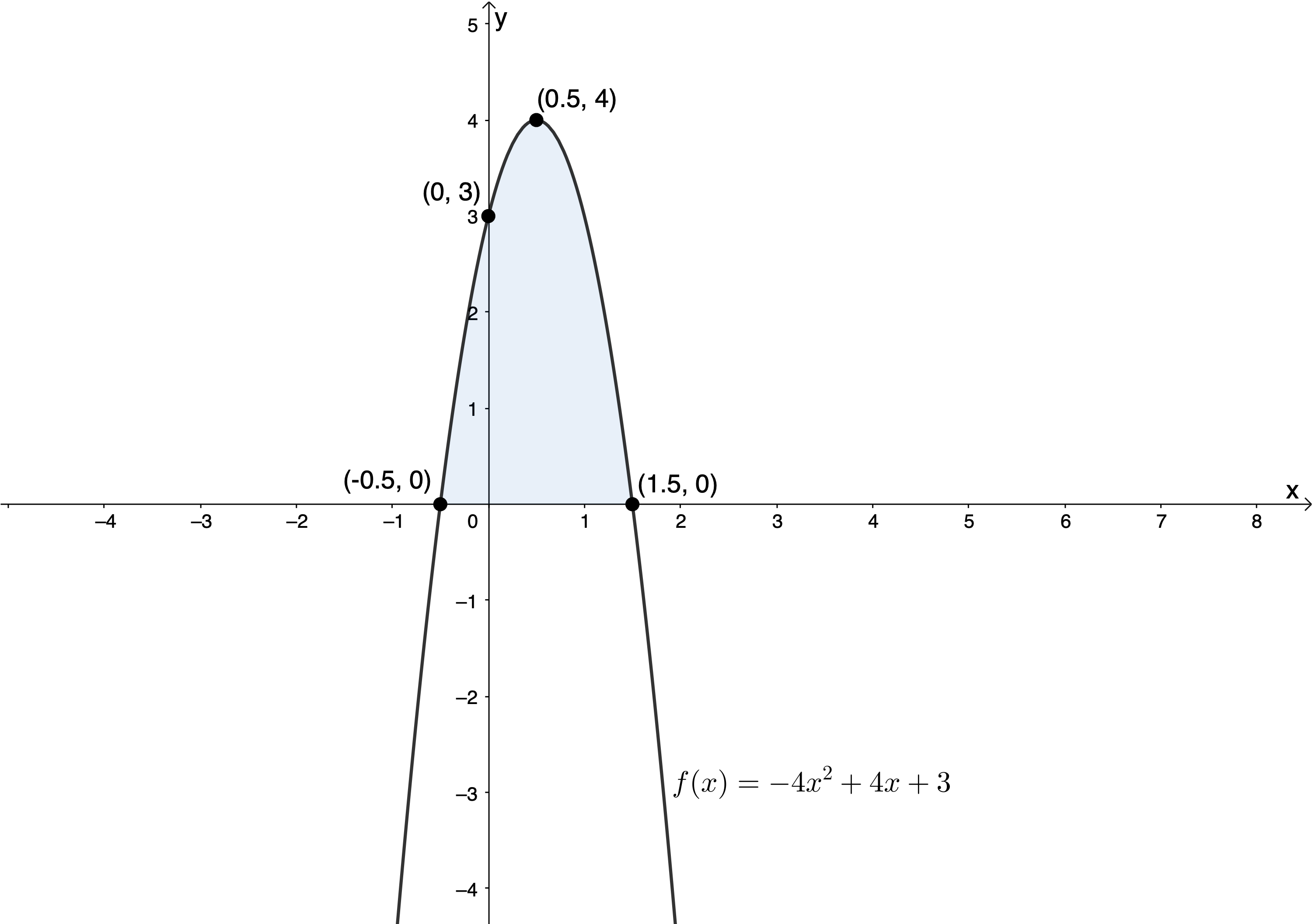
However, if we were solving this inequality algebraically, we would probably proceed as follows:
[latex]\scriptsize \begin{align*}-4{{x}^{2}}+4x+3 & \ge 0\quad \text{Multiply through by }-1\text{ and reverse the inequality}\\\therefore 4{{x}^{2}}-4x+3 & \le 0\end{align*}[/latex]
Now you might be wondering how changing the function from [latex]\scriptsize f(x)=-4{{x}^{2}}+4x+3[/latex] to another function, for example [latex]\scriptsize g(x)=4{{x}^{2}}-4x-3[/latex], will not result in a completely different solution. The answer lies in the importance of reversing the inequality sign whenever we multiply both sides of an inequality by a negative number. If we look at a sketch of [latex]\scriptsize g(x)=4{{x}^{2}}-4x-3[/latex] we can see why (see Figure7).
Because we reversed the inequality sign, we are now interested in where [latex]\scriptsize 4{{x}^{2}}-4x-3\le 0[/latex], where [latex]\scriptsize g(x)\le 0[/latex] or where [latex]\scriptsize g(x)[/latex] is below the x-axis.
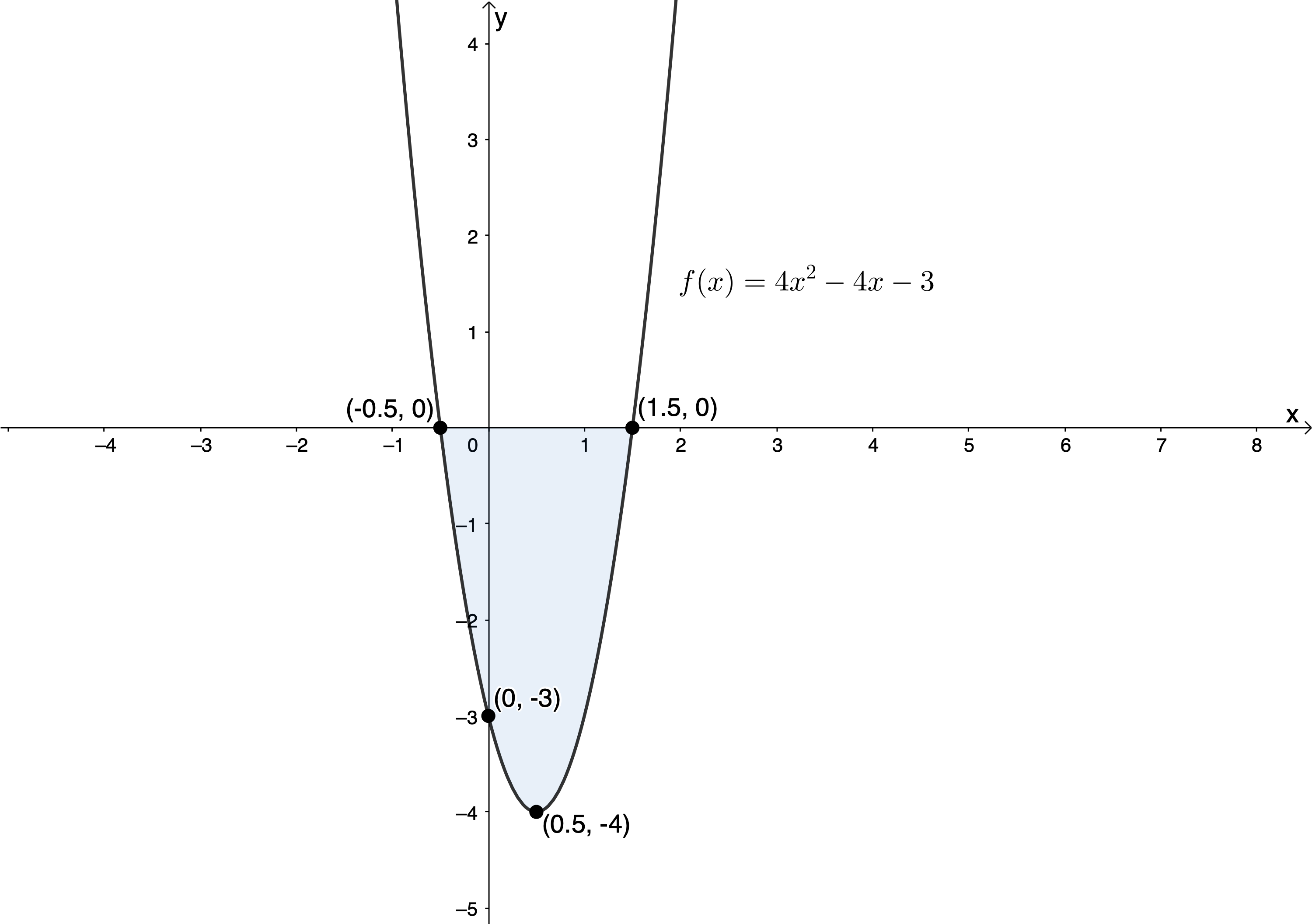
We can see that we get exactly the same solution: [latex]\scriptsize x\in [-\displaystyle \frac{1}{2},\displaystyle \frac{3}{2}][/latex] or [latex]\scriptsize \{x|x\in \mathbb{R}\text{,}-\displaystyle \frac{1}{2}\le x\le \displaystyle \frac{3}{2}\}[/latex].
Solve inequalities with unknowns in the denominator
The process of solving quadratic inequalities when there are fractions involved and where the denominators contain variables is slightly different.
If we were asked to solve for [latex]\scriptsize x[/latex] in [latex]\scriptsize \displaystyle \frac{4}{{x-3}}=\displaystyle \frac{5}{{x+4}}[/latex], we would multiply both sides by the LCD of [latex]\scriptsize (x-3)(x+4)[/latex] to get:
[latex]\scriptsize \begin{align*}\displaystyle \frac{4}{{x-3}} & =\displaystyle \frac{5}{{x+4}},x\ne 3,x\ne -4\\\therefore 4(x+4) & =5(x-3)\\\therefore 4x+16 & =5x-15\\\therefore x & =31\end{align*}[/latex]
We can do this because we don’t need to worry about whether [latex]\scriptsize (x-3) \lt 0[/latex] or whether [latex]\scriptsize (x+4) \lt 0[/latex]. But if we have an inequality, we know we have to flip the inequality around if we multiply through by a negative number. Because we don’t know if [latex]\scriptsize (x-3) \lt 0[/latex] or if [latex]\scriptsize (x+4) \lt 0[/latex] we don’t know whether to flip the inequality around or not. So, we need a different method.
Example 5.4
Solve for [latex]\scriptsize x[/latex] in [latex]\scriptsize \displaystyle \frac{4}{{x-3}}\le \displaystyle \frac{5}{{x+4}}[/latex].
Solution
Step 1: Get one side of the inequality equal to zero
To make sure that we don’t have to multiply through by the LCD, we rearrange the inequality to get one side equal to zero.
[latex]\scriptsize \begin{align*}\displaystyle \frac{4}{{x-3}} & \le \displaystyle \frac{5}{{x+4}}\quad \text{Subtract }\displaystyle \frac{5}{{x+4}}\text{ from both sides}\\\therefore \displaystyle \frac{4}{{x-3}}-\displaystyle \frac{5}{{x+4}} & \le 0\end{align*}[/latex]
Step 2: Add the fractions
Next, we need to subtract the fractions on the other side of the inequality.
[latex]\scriptsize \begin{align*}\displaystyle \frac{4}{{x-3}}-\displaystyle \frac{5}{{x+4}} & \le 0\\\therefore \displaystyle \frac{{4(x+4)-5(x-3)}}{{(x-3)(x+4)}} & \le 0\\\therefore \displaystyle \frac{{4x+16-5x+15}}{{(x-3)(x+4)}} & \le 0\\\therefore \displaystyle \frac{{-x+31}}{{(x-3)(x+4)}} & \le 0\quad \text{We can leave the LHS as it is, or multiply through by }-1\\\therefore \displaystyle \frac{{-(x-31)}}{{(x-3)(x+4)}} & \le 0\\\therefore \displaystyle \frac{{(x-31)}}{{(x-3)(x+4)}} & \ge 0\quad \text{Remember to flip the inequality sign}\end{align*}[/latex]
Step 3: Determine the critical values
The critical values now are not just the roots (those values that make the expression on the LHS equal to zero) but also the restrictions (those values that make the expression on the LHS undefined).
Our critical values are [latex]\scriptsize x=31[/latex], [latex]\scriptsize x=3[/latex] and [latex]\scriptsize x=-4[/latex].
Step 4: Complete a table of signs
Notice how we need to add additional columns to accommodate the extra critical value. As before, choose values for [latex]\scriptsize x[/latex] to complete the table.
| [latex]\scriptsize x \lt -4[/latex] | [latex]\scriptsize x=-4[/latex] | [latex]\scriptsize -4 \lt x \lt 3[/latex] | [latex]\scriptsize x=3[/latex] | [latex]\scriptsize 3 \lt x \lt 31[/latex] | [latex]\scriptsize x=31[/latex] | [latex]\scriptsize x \gt 31[/latex] | |
| [latex]\scriptsize \displaystyle \frac{{(x-31)}}{{(x-3)(x+4)}}[/latex] | [latex]\scriptsize -[/latex] | Undefined | [latex]\scriptsize +[/latex] | Undefined | [latex]\scriptsize -[/latex] | [latex]\scriptsize 0[/latex] | [latex]\scriptsize +[/latex] |
Step 5: Read off the solution
We are solving for [latex]\scriptsize \displaystyle \frac{{(x-31)}}{{(x-3)(x+4)}} \ge 0[/latex]. Which ranges result in a positive expression? These are:
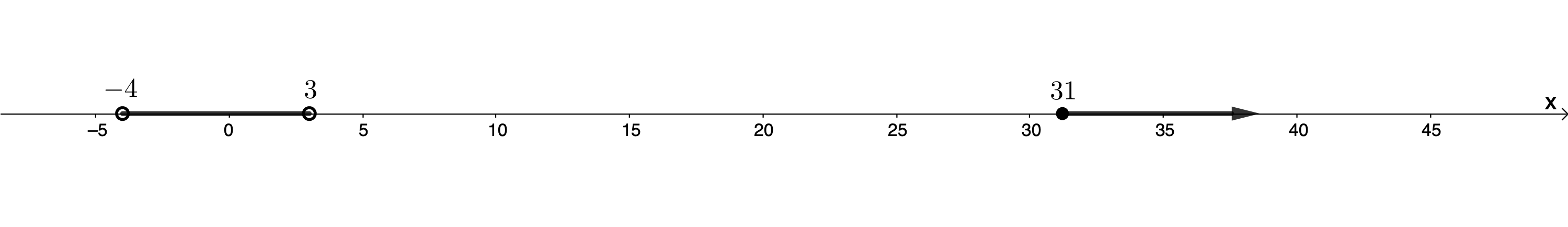
[latex]\scriptsize x\in (-4,3)\bigcup [31,\infty )[/latex]
[latex]\scriptsize \{x|x\in \mathbb{R},-4 \lt x \lt 3,x\ge 31\}[/latex]
Note: Even though we are solving for a greater than or equal to inequality, we cannot include [latex]\scriptsize -4[/latex] or [latex]\scriptsize 3[/latex] in our solutions because these values make the expression undefined.
Exercise 5.2
Solve for [latex]\scriptsize x[/latex] in the following inequalities and represent your answers using interval and set builder notation:
- [latex]\scriptsize \displaystyle \frac{4}{{x-3}}\ge 1[/latex]
- [latex]\scriptsize \displaystyle \frac{{15-x}}{x}\ge 2x[/latex]
- [latex]\scriptsize \displaystyle \frac{{-4}}{{(x-3)(x-1)}} \lt 3[/latex]
- [latex]\scriptsize \displaystyle \frac{{{{x}^{2}}+3}}{{3x-2}}\le 0[/latex]
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- How to find the critical values.
- How to solve quadratic inequalities using the table method.
- How to solve quadratic inequalities using the graphical method.
- How to represent the solution to a quadratic inequality on a number line.
- How to solve inequalities with fractions where there are unknowns in the denominator.
Unit 5: Assessment
Suggested time to complete: 60 minutes
- Solve for [latex]\scriptsize x[/latex] in the following inequalities and represent your answers as indicated:
- [latex]\scriptsize 2+x-{{x}^{2}}\le 0[/latex] (represent your answer on a number line)
- [latex]\scriptsize (x-1)(x-2) \lt 6[/latex] (represent your answer using set builder notation)
- [latex]\scriptsize -10x \lt -{{x}^{2}}[/latex] (represent your answer using set builder notation)
- [latex]\scriptsize \displaystyle \frac{{{{x}^{2}}+4}}{{x-7}}\le 0,x\ne 7[/latex] (represent your answer using interval notation)
- [latex]\scriptsize {{x}^{2}}+4x \lt -4[/latex] (represent your answer using set builder notation)
- [latex]\scriptsize \displaystyle \frac{{x+2}}{x} \gt 1,x\ne 0[/latex] (represent your answer using interval notation)
- Solve for [latex]\scriptsize x[/latex] in [latex]\scriptsize -6\le {{x}^{2}}-5x\le 6[/latex] and represent your answer on a number line.
Hint: Split the expression into two separate inequalities first.
The full solutions are at the end of the unit.
Unit 5: Solutions
Exercise 5.1
- .
[latex]\scriptsize \begin{align*}{{x}^{2}}+2x-15 & \lt 0\\\therefore (x-3)(x+5) & \lt 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=-5[/latex] and [latex]\scriptsize x=3[/latex][latex]\scriptsize x \lt -5[/latex] [latex]\scriptsize x=-5[/latex] [latex]\scriptsize -5 \lt x \lt 3[/latex] [latex]\scriptsize x=3[/latex] [latex]\scriptsize x \gt 3[/latex] [latex]\scriptsize (x-3)(x+5)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize \{x|x\in \mathbb{R},-5 \lt x \lt 3\}[/latex]
- .
[latex]\scriptsize \begin{align*}10{{x}^{2}} & \le 31x-15\\\therefore 10{{x}^{2}}-31x+15 & \le 0\\\therefore (2x-5)(5x-3) & \le 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=\displaystyle \frac{5}{2}[/latex] and [latex]\scriptsize x=\displaystyle \frac{3}{5}[/latex][latex]\scriptsize x \lt \displaystyle \frac{3}{5}[/latex] [latex]\scriptsize x=\displaystyle \frac{3}{5}[/latex] [latex]\scriptsize \displaystyle \frac{3}{5} \lt x \lt \displaystyle \frac{5}{2}[/latex] [latex]\scriptsize x=\displaystyle \frac{5}{2}[/latex] [latex]\scriptsize x \gt \displaystyle \frac{5}{2}[/latex] [latex]\scriptsize (2x-5)(5x-3)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize x\in [\displaystyle \frac{3}{5},\displaystyle \frac{5}{2}][/latex]
- .
[latex]\scriptsize \begin{align*}9x(x+1) & \gt 10\\\therefore 9{{x}^{2}}+9x-10 & \gt 0\\\therefore (3x-2)(3x+5) & \gt 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=\displaystyle \frac{2}{3}[/latex] and [latex]\scriptsize x=-\displaystyle \frac{5}{3}[/latex][latex]\scriptsize x \lt -\displaystyle \frac{5}{3}[/latex] [latex]\scriptsize x=-\displaystyle \frac{5}{3}[/latex] [latex]\scriptsize -\displaystyle \frac{5}{3} \lt x \lt \displaystyle \frac{2}{3}[/latex] [latex]\scriptsize x=\displaystyle \frac{2}{3}[/latex] [latex]\scriptsize x \gt \displaystyle \frac{2}{3}[/latex] [latex]\scriptsize (3x-2)(3x+5)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize x\in (-\infty ,-\displaystyle \frac{5}{3})\bigcup (\displaystyle \frac{2}{3},\infty )[/latex]
- .
[latex]\scriptsize \begin{align*}5(2{{x}^{2}}-7) & \lt 11x\\\therefore 10{{x}^{2}}-11x-35 & \lt 0\\\therefore (5x+7)(2x-5) & \lt 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=-\displaystyle \frac{7}{5}[/latex] and [latex]\scriptsize x=\displaystyle \frac{5}{2}[/latex][latex]\scriptsize x \lt -\displaystyle \frac{7}{5}[/latex] [latex]\scriptsize x=-\displaystyle \frac{7}{5}[/latex] [latex]\scriptsize -\displaystyle \frac{7}{5} \lt x \lt \displaystyle \frac{5}{2}[/latex] [latex]\scriptsize x=\displaystyle \frac{5}{2}[/latex] [latex]\scriptsize x \gt \displaystyle \frac{5}{2}[/latex] [latex]\scriptsize (5x+7)(2x-5)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize \{x|x\in \mathbb{R}\text{,}-\displaystyle \frac{7}{5} \lt x \lt \displaystyle \frac{5}{2}\}[/latex]
- .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{40x-21}}{{{{x}^{2}}}} & \ge 16,{{x}^{2}}\ne 0\therefore x\ne 0\\\text{You can multiply both sides by }{{x}^{2}}\text{ because we know that }{{x}^{2}} \gt 0\\\therefore 40x-21 & \ge 16{{x}^{2}}\\\therefore 16{{x}^{2}}-40x+21 & \le 0\quad \text{Be careful of the direction of the inequality}\\\therefore (4x-3)(4x-7) & \le 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=\displaystyle \frac{3}{4}[/latex] and [latex]\scriptsize x=\displaystyle \frac{7}{4}[/latex][latex]\scriptsize x \lt \displaystyle \frac{3}{4}[/latex] [latex]\scriptsize x=\displaystyle \frac{3}{4}[/latex] [latex]\scriptsize \displaystyle \frac{3}{4} \lt x \lt \displaystyle \frac{7}{4}[/latex] [latex]\scriptsize x=\displaystyle \frac{7}{4}[/latex] [latex]\scriptsize x \gt \displaystyle \frac{7}{4}[/latex] [latex]\scriptsize (4x-3)(4x-7)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] 
Exercise 5.2
- .
[latex]\scriptsize \begin{align*}\displaystyle \frac{4}{{x-3}} & \ge 1,x\ne 3\\\therefore \displaystyle \frac{4}{{x-3}}-1 & \ge 0\\\therefore \displaystyle \frac{{4-(x-3)}}{{(x-3)}} & \ge 0\\\therefore \displaystyle \frac{{-x+7}}{{(x-3)}} & \ge 0\quad \text{Multiply through by }-1\text{ and reverse the inequality sign}\\\therefore \displaystyle \frac{{x-7}}{{(x-3)}} & \le 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=7[/latex] and [latex]\scriptsize x=3[/latex][latex]\scriptsize x \lt 3[/latex] [latex]\scriptsize x=3[/latex] [latex]\scriptsize 3 \lt x \lt 7[/latex] [latex]\scriptsize x=7[/latex] [latex]\scriptsize x \gt 7[/latex] [latex]\scriptsize \displaystyle \frac{{(x-7)}}{{(x-3)}}[/latex] [latex]\scriptsize +[/latex] Undefined [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize x\in (3,7][/latex]
[latex]\scriptsize \{x|x\in \mathbb{R},3 \lt x\le 7\}[/latex] Remember that we cannot include [latex]\scriptsize 3[/latex] in our solution. - .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{15-x}}{x} & \ge 2x,x\ne 0\\\therefore \displaystyle \frac{{15-x}}{x}-2x & \ge 0\\\therefore \displaystyle \frac{{15-x-2{{x}^{2}}}}{x} & \ge 0\\\therefore \displaystyle \frac{{(3-x)(5+2x)}}{x} & \ge 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=3[/latex], [latex]\scriptsize x=-\displaystyle \frac{5}{2}[/latex] and [latex]\scriptsize x=0[/latex][latex]\scriptsize x \lt -\displaystyle \frac{5}{2}[/latex] [latex]\scriptsize x=-\displaystyle \frac{5}{2}[/latex] [latex]\scriptsize -\displaystyle \frac{5}{2} \lt x \lt 0[/latex] [latex]\scriptsize x=0[/latex] [latex]\scriptsize 0 \lt x \lt 3[/latex] [latex]\scriptsize x=3[/latex] [latex]\scriptsize x \gt 3[/latex] [latex]\scriptsize \displaystyle \frac{{(3-x)(5+2x)}}{x}[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] Undef [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize x\in (-\infty ,-\displaystyle \frac{5}{2}]\bigcup (0,3][/latex]
[latex]\scriptsize \{x|x\in \mathbb{R},x\le -\displaystyle \frac{5}{2},0 \lt x\le 3\}[/latex] - .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{-3}}{{(x-3)(x-1)}} & \lt 3,x\ne 3,x\ne 1\\\therefore \displaystyle \frac{{-3}}{{(x-3)(x-1)}}-3 & \lt 0\\\therefore \displaystyle \frac{{-3-3(x-3)(x-1)}}{{(x-3)(x-1)}} & \lt 0\\\therefore \displaystyle \frac{{-3-3({{x}^{2}}-4x+3)}}{{(x-3)(x-1)}} & \lt 0\\\therefore \displaystyle \frac{{-3-3{{x}^{2}}+12x-9}}{{(x-3)(x-1)}} & \lt 0\\\therefore \displaystyle \frac{{-3{{x}^{2}}+12x-12}}{{(x-3)(x-1)}} & \lt 0\quad \text{Multiply through by }-1\text{ and reverse the inequality}\\\therefore \displaystyle \frac{{3{{x}^{2}}-12x+12}}{{(x-3)(x-1)}} & \gt 0\quad \text{You can take out a common factor of }3\text{ or factorise as is}\\\therefore \displaystyle \frac{{(3x-6)(x-2)}}{{(x-3)(x-1)}} & \gt 0\\\therefore \displaystyle \frac{{3(x-2)(x-2)}}{{(x-3)(x-1)}} & \gt 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=1[/latex], [latex]\scriptsize x=2[/latex] and [latex]\scriptsize x=3[/latex][latex]\scriptsize x \lt 1[/latex] [latex]\scriptsize x=1[/latex] [latex]\scriptsize 1 \lt x \lt 2[/latex] [latex]\scriptsize x=2[/latex] [latex]\scriptsize 2 \lt x \lt 3[/latex] [latex]\scriptsize x=3[/latex] [latex]\scriptsize x \gt 3[/latex] [latex]\scriptsize \displaystyle \frac{{3(x-2)(x-2)}}{{(x-3)(x-1)}}[/latex] [latex]\scriptsize +[/latex] Undef [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] Undef [latex]\scriptsize +[/latex] [latex]\scriptsize x\in (-\infty ,1)\bigcup \text{(3,}\infty )[/latex]
[latex]\scriptsize \{x|x\in \mathbb{R},x \lt 1,x \gt 3\}[/latex]
.
You could also recognise that the numerator [latex]\scriptsize 3{{(x-2)}^{2}}\ge 0[/latex]. Therefore for the fraction to be positive, the denominator must be positive. Hence, you could consider a condensed table of critical values.[latex]\scriptsize x \lt 1[/latex] [latex]\scriptsize x=1[/latex] [latex]\scriptsize 1 \lt x \lt 3[/latex] [latex]\scriptsize x=3[/latex] [latex]\scriptsize x \gt 3[/latex] [latex]\scriptsize \displaystyle \frac{{3(x-2)(x-2)}}{{(x-3)(x-1)}}[/latex] [latex]\scriptsize +[/latex] Undef [latex]\scriptsize -[/latex] Undef [latex]\scriptsize +[/latex] - .
[latex]\scriptsize \displaystyle \frac{{{{x}^{2}}+3}}{{3x-2}}\le 0,x\ne \displaystyle \frac{2}{3}[/latex]
[latex]\scriptsize {{x}^{2}}\ge 0\therefore {{x}^{2}}+3\ge 3[/latex]. Therefore, the numerator is always positive.
Critical values: [latex]\scriptsize x=\displaystyle \frac{2}{3}[/latex][latex]\scriptsize x \lt \displaystyle \frac{2}{3}[/latex] [latex]\scriptsize x=\displaystyle \frac{2}{3}[/latex] [latex]\scriptsize x \gt \displaystyle \frac{2}{3}[/latex] [latex]\scriptsize \displaystyle \frac{{{{x}^{2}}+3}}{{3x-2}}[/latex] [latex]\scriptsize -[/latex] Undef [latex]\scriptsize +[/latex] [latex]\scriptsize x\in (-\infty ,\displaystyle \frac{2}{3})[/latex]
[latex]\scriptsize \{x|x\in \mathbb{R},x \lt \displaystyle \frac{2}{3}\}[/latex]
Unit 5: Assessment
- .
- .
[latex]\scriptsize \begin{align*}2+x-{{x}^{2}} & \le 0\\\therefore {{x}^{2}}-x-2 & \ge 0\\\therefore (x+1)(x-2) & \ge 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=-1[/latex] and [latex]\scriptsize x=2[/latex][latex]\scriptsize x \lt -1[/latex] [latex]\scriptsize x=-1[/latex] [latex]\scriptsize -1 \lt x \lt 2[/latex] [latex]\scriptsize x=2[/latex] [latex]\scriptsize x \gt 2[/latex] [latex]\scriptsize (x+1)(x-2)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] 
- .
[latex]\scriptsize \begin{align*}(x-1)(x-2) & \lt 6\\\therefore {{x}^{2}}-3x+2-6 & \lt 0\\\therefore {{x}^{2}}-3x-4 & \lt 0\\\therefore (x+1)(x-4) & \lt 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=-1[/latex] and [latex]\scriptsize x=4[/latex][latex]\scriptsize x \lt -1[/latex] [latex]\scriptsize x=-1[/latex] [latex]\scriptsize -1 \lt x \lt 4[/latex] [latex]\scriptsize x=4[/latex] [latex]\scriptsize x \gt 4[/latex] [latex]\scriptsize (x+1)(x-4)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize \{x|x\in \mathbb{R},-1 \lt x \lt 4\}[/latex]
- .
[latex]\scriptsize \begin{align*}-10x & \lt -{{x}^{2}}\\\therefore {{x}^{2}}-10x & \lt 0\\\therefore x(x-10) & \lt 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=0[/latex] and [latex]\scriptsize x=10[/latex][latex]\scriptsize x \lt 0[/latex] [latex]\scriptsize x=0[/latex] [latex]\scriptsize 0 \lt x \lt 10[/latex] [latex]\scriptsize x=10[/latex] [latex]\scriptsize x \gt 10[/latex] [latex]\scriptsize x(x-10)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize \{x|x\in \mathbb{R},0 \lt x \lt 10\}[/latex]
- .
[latex]\scriptsize \displaystyle \frac{{{{x}^{2}}+4}}{{x-7}}\le 0,x\ne 7[/latex]
[latex]\scriptsize {{x}^{2}}\ge 0\therefore {{x}^{2}}+4\ge 4[/latex]. The numerator is always positive.
Critical value: [latex]\scriptsize x=7[/latex][latex]\scriptsize x \lt 7[/latex] [latex]\scriptsize x=7[/latex] [latex]\scriptsize x \gt 7[/latex] [latex]\scriptsize \displaystyle \frac{{{{x}^{2}}+4}}{{x-7}}[/latex] [latex]\scriptsize -[/latex] Undefined [latex]\scriptsize +[/latex] [latex]\scriptsize x\in (-\infty ,7)[/latex]
- .
[latex]\scriptsize \begin{align*}{{x}^{2}}+4x & \lt -4\\\therefore {{x}^{2}}+4x+4 & \lt 0\\\therefore (x+2)(x+2) & \lt 0\end{align*}[/latex]
Critical value: [latex]\scriptsize x=-2[/latex][latex]\scriptsize x \lt -2[/latex] [latex]\scriptsize x=-2[/latex] [latex]\scriptsize x \gt -2[/latex] [latex]\scriptsize (x+2)(x+2)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] No solution
.
Alternative approach:
[latex]\scriptsize \begin{align*}{{x}^{2}}+4x & \lt -4\\\therefore {{x}^{2}}+4x+4 & \lt 0\\\therefore (x+2)(x+2) & \lt 0\\\therefore {{(x+2)}^{2}} & \lt 0\end{align*}[/latex]
But [latex]\scriptsize {{(x+2)}^{2}}[/latex] is always positive. Therefore, there is no solution. - .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{x+2}}{x} & \gt 1,x\ne 0\\\therefore \displaystyle \frac{{x+2}}{x}-1 & \gt 0\\\therefore \displaystyle \frac{{x+2-x}}{x} & \gt 0\\\therefore \displaystyle \frac{2}{x} & \gt 0\end{align*}[/latex]
Critical value: [latex]\scriptsize x=0[/latex][latex]\scriptsize x \lt 0[/latex] [latex]\scriptsize x=0[/latex] [latex]\scriptsize x \gt 0[/latex] [latex]\scriptsize \displaystyle \frac{2}{x}[/latex] [latex]\scriptsize -[/latex] Undefined [latex]\scriptsize +[/latex] [latex]\scriptsize x\in (0,\infty )[/latex]
- .
- .
[latex]\scriptsize -6\le {{x}^{2}}-5x\le 6[/latex]
[latex]\scriptsize -6\le {{x}^{2}}-5x[/latex] (1)
[latex]\scriptsize {{x}^{2}}-5x\le 6[/latex] (2)
.
From (1):
[latex]\scriptsize \begin{align*}-6 & \le {{x}^{2}}-5x\\\therefore {{x}^{2}}-5x+6 & \ge 0\\\therefore (x-2)(x-3) & \ge 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=2[/latex] and [latex]\scriptsize x=3[/latex][latex]\scriptsize x \lt 2[/latex] [latex]\scriptsize x=2[/latex] [latex]\scriptsize 2 \lt x \lt 3[/latex] [latex]\scriptsize x=3[/latex] [latex]\scriptsize x \gt 3[/latex] [latex]\scriptsize (x-2)(x-3)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] From (2):
[latex]\scriptsize \begin{align*}{{x}^{2}}-5x & \le 6\\\therefore {{x}^{2}}-5x-6 & \le 0\\\therefore (x+1)(x-6) & \le 0\end{align*}[/latex]
Critical values: [latex]\scriptsize x=-1[/latex] and [latex]\scriptsize x=6[/latex][latex]\scriptsize x \lt -1[/latex] [latex]\scriptsize x=-1[/latex] [latex]\scriptsize -1 \lt x \lt 6[/latex] [latex]\scriptsize x=6[/latex] [latex]\scriptsize x \gt 6[/latex] [latex]\scriptsize (x-1)(x-6)[/latex] [latex]\scriptsize +[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize -[/latex] [latex]\scriptsize 0[/latex] [latex]\scriptsize +[/latex] If we plot the results of the two sign tables above on the same number line, we get the following. We can see that the regions overlap (make [latex]\scriptsize -6\le {{x}^{2}}-5x[/latex] AND [latex]\scriptsize {{x}^{2}}-5x\le 6[/latex] at the same time) when [latex]\scriptsize -1\le x\le 2[/latex] or when [latex]\scriptsize 3\le x\le 6[/latex].
 Therefore, the final solution is [latex]\scriptsize x\in [-1,2]\bigcup [3,6][/latex].
Therefore, the final solution is [latex]\scriptsize x\in [-1,2]\bigcup [3,6][/latex].

Media Attributions
- figure1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example5.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example5.2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example5.3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure6 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure7 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example5.4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise5.1A4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentA1a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentA2part1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentA2part2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
