Unit outcomes

By the end of this unit you will be able to:

• Express complex numbers in polar form.
• Convert complex numbers from standard/rectangular form to polar form.
• Convert complex numbers from polar form to standard/rectangular form.

What you should know

Before you start this unit, make sure you can:

• Represent complex numbers using an Argand diagram. Refer to unit 2 in this subject outcome if you need help with this.
• Find the modulus of a complex number. Refer to unit 2 in this subject outcome if you need help with this.
• Find the argument of a complex number. Refer to unit 2 in this subject outcome if you need help with this.

Introduction

We saw in the previous unit that we can represent complex numbers on the complex plane. These are referred to as Argand diagrams. Figure 1 shows the complex number [latex]\scriptsize z=2-3i[/latex] represented in this way, where the complex number is represented as the point [latex]\scriptsize (x,y)=(2,-3)[/latex].

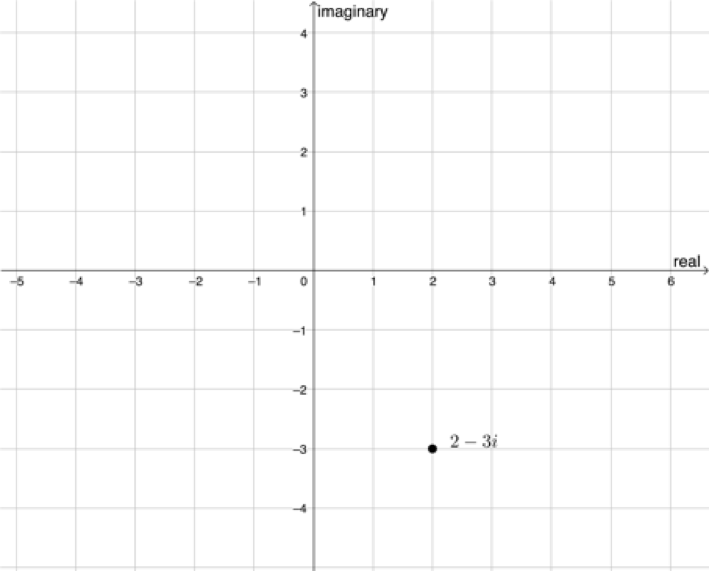
We also saw that we can calculate the length of the line joining the point representing a complex number with the origin. This is called the absolute value or modulus of the complex number and is represented as [latex]\scriptsize \left| z \right|[/latex]. The modulus of [latex]\scriptsize z=2-3i[/latex] is calculated as follows:

[latex]\scriptsize \begin{align*}\left| z \right| & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{2}^{2}}+{{{(-3)}}^{2}}}}\\ & =\sqrt{{4+9}}\\ & =\sqrt{{13}}\end{align*}[/latex]

We noted that it is not enough to know just the modulus of a complex number. We also need to know the angle that the line representing the modulus makes with the positive x-axis (or positive real axis). This angle is called the argument.

We can calculate the argument using either of the following trigonometric ratios:
[latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex] or [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}[/latex] where [latex]\scriptsize r[/latex] (the radius of the circle with centre the origin, passing through the point [latex]\scriptsize (x,y)[/latex] representing the complex number) has the same value as [latex]\scriptsize \left| z \right|[/latex].

In the case above the argument is calculated as:

[latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{y}{r}=\displaystyle \frac{{-3}}{{\sqrt{{13}}}}\\ & \therefore \theta ={{303.69}^\circ}\quad \text{The point is in the fourth quadrant}\end{align*}[/latex]

With all of this knowledge, we are ready to work with complex numbers in polar form.

Complex numbers in polar form

We say that [latex]\scriptsize z=2-3i[/latex] is written in standard or rectangular form where the number is expressed in terms of a real and an imaginary component. The polar form of a complex number expresses the number in terms of its modulus and argument.

Suppose we have a complex number [latex]\scriptsize z=x+yi[/latex]. We can represent this with an Argand diagram as shown in Figure 2.

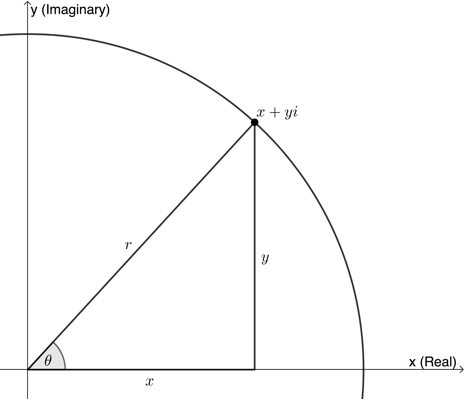
Now we know that [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}[/latex] and [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex]. Therefore, [latex]\scriptsize x=r\cos \theta[/latex] and [latex]\scriptsize y=r\sin \theta[/latex].

So, the point [latex]\scriptsize (x,y)[/latex] has coordinates given by [latex]\scriptsize x=r\cos \theta[/latex] and [latex]\scriptsize y=r\sin \theta[/latex] where [latex]\scriptsize r=\sqrt{{{{x}^{2}}+{{y}^{2}}}}[/latex]. Therefore:

[latex]\scriptsize \begin{align*}z & =x+yi\\ & =r\cos \theta +(r\sin \theta )i\\ & =r(\cos \theta +i\sin \theta )\end{align*}[/latex]

Take note!

We often use the abbreviation [latex]\scriptsize r\text{cis}\theta[/latex] to represent [latex]\scriptsize r(\cos \theta +i\sin \theta )[/latex].

Example 3.1

Find the polar form of [latex]\scriptsize z=4+4i[/latex].

Solution

Step 1: Find the value of [latex]\scriptsize r[/latex] (or [latex]\scriptsize \left| z \right|[/latex] or the modulus)

[latex]\scriptsize \begin{align*}r & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{4}^{2}}+{{4}^{2}}}}\\ & =\sqrt{{16+16}}\\ & =\sqrt{{32}}\quad 32=16\times 2\\ & =4\sqrt{2}\end{align*}[/latex]

Step 2: Find the value of [latex]\scriptsize \theta[/latex] (the argument)

[latex]\scriptsize \begin{align*}\cos \theta & =\displaystyle \frac{x}{r}=\displaystyle \frac{4}{{4\sqrt{2}}}=\displaystyle \frac{1}{{\sqrt{2}}}\\ & \therefore \theta ={{45}^\circ}\end{align*}[/latex]

In this case, we used the special angle of [latex]\scriptsize {{45}^\circ}[/latex]. We know the point is in the first quadrant so we do not need to transform the angle to another quadrant.

Note that we could also have used [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex] to find the argument.

Step 3: Write the solution

[latex]\scriptsize \begin{align*}z & =r(\cos \theta +i\sin \theta )\\ & =4\sqrt{2}(\cos {{45}^\circ}+i\sin {{45}^\circ})\\ & =4\sqrt{2}cis{{45}^\circ}\end{align*}[/latex]

Take note!

When finding the argument, remember that you need to pay attention to which quadrant the complex number is in. A useful strategy can be to make the ratio for [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}[/latex] (or [latex]\scriptsize \sin \theta =\displaystyle \frac{y}{r}[/latex]) positive, in order to find the reference acute angle [latex]\scriptsize \alpha[/latex], and then to transfer this angle into the necessary quadrant as follows:

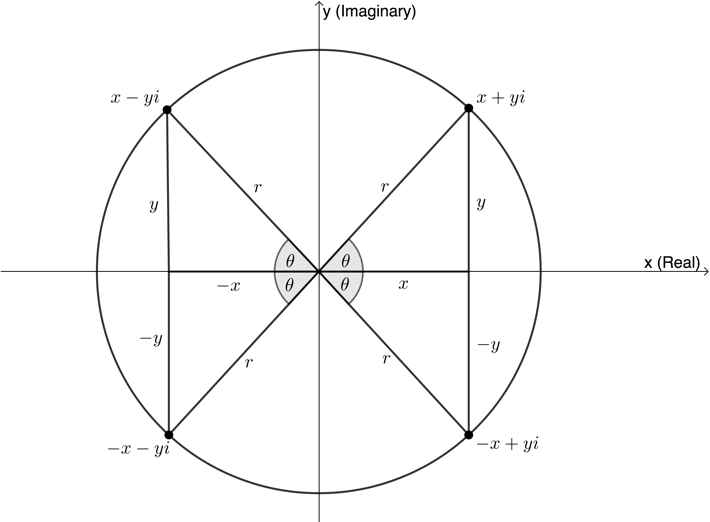
• Second quadrant: [latex]\scriptsize {{180}^\circ}-\alpha[/latex]
• Third quadrant: [latex]\scriptsize {{180}^\circ}+\alpha[/latex]
• Fourth quadrant: [latex]\scriptsize {{360}^\circ}-\alpha[/latex]

Example 3.2

Find the polar form of [latex]\scriptsize z=-4-4i[/latex].

Solution

Step 1: Find the value of [latex]\scriptsize r[/latex] (or [latex]\scriptsize \left| z \right|[/latex] or the modulus)

[latex]\scriptsize \begin{align*}r & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{{(-4)}}^{2}}+{{{(-4)}}^{2}}}}\\ & =\sqrt{{16+16}}\\ & =\sqrt{{32}}\\ & =4\sqrt{2}\end{align*}[/latex]

Step 2: Find the value of [latex]\scriptsize \theta[/latex] (the argument)

[latex]\scriptsize z[/latex] is in the third quadrant. Find the reference angle [latex]\scriptsize \alpha[/latex].
[latex]\scriptsize \cos \alpha =\displaystyle \frac{x}{r}=\displaystyle \frac{4}{{4\sqrt{2}}}=\displaystyle \frac{1}{{\sqrt{2}}}[/latex]

While we can use the special angle of [latex]\scriptsize {{45}^\circ}[/latex], we need to recognise that the point lies in the third quadrant where the ratios for cosine and sine are negative. Both the [latex]\scriptsize x[/latex] (or real) and [latex]\scriptsize y[/latex] (or imaginary) components are negative.

So while the reference angle is [latex]\scriptsize {{45}^\circ}[/latex], we need to move this into the third quadrant by adding [latex]\scriptsize {{180}^\circ}[/latex] to it. Therefore [latex]\scriptsize \theta ={{180}^\circ}+{{45}^\circ}={{225}^\circ}[/latex].

Step 3: Write the solution

[latex]\scriptsize \begin{align*}z & =r(\cos \theta +i\sin \theta )\\ & =4\sqrt{2}(\cos {{225}^\circ}+i\sin {{225}^\circ})\\ & =4\sqrt{2}\text{cis22}{{5}^\circ}\end{align*}[/latex]

Remember that this is just a shorthand expression for the full polar form of [latex]\scriptsize z=4\sqrt{2}(cos{{225}^\circ}+i\sin {{225}^\circ})[/latex].

Exercise 3.1

Write the following complex numbers in polar form:

1. [latex]\scriptsize z=5-12i[/latex]
2. [latex]\scriptsize z=-7+2i[/latex]

The full solutions are at the end of the unit.

Convert polar form to rectangular form

Sometimes it is necessary to convert a complex number in polar form into standard or rectangular form. To do this, we need to first evaluate the trigonometric functions [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex], then multiply through by [latex]\scriptsize r[/latex].

Example 3.3

Convert [latex]\scriptsize z=12\text{cis}{{30}^\circ}[/latex] into standard/rectangular form.

Solution

Step 1: Evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex]

We can use the fact that [latex]\scriptsize {{30}^\circ}[/latex] is a special angle to evaluate without a calculator.

[latex]\scriptsize \cos {{30}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex]
[latex]\scriptsize \sin {{30}^\circ}=\displaystyle \frac{1}{2}[/latex]

Step 2: Find the standard form

We know that the complex number is in the first quadrant where cosine and sine are both positive.

[latex]\scriptsize \begin{align*}z & =12(\cos {{30}^\circ}+i\sin {{30}^\circ})\\ & =12\left( {\displaystyle \frac{{\sqrt{3}}}{2}+\displaystyle \frac{1}{2}i} \right)\\ & =\displaystyle \frac{{12\sqrt{3}}}{2}+6i\\ & =6\sqrt{3}+6i\end{align*}[/latex]

The complex number in standard form is [latex]\scriptsize z=6\sqrt{3}+6i[/latex].

Example 3.4

Convert [latex]\scriptsize z=4\text{cis12}{{\text{0}}^\circ}[/latex] into standard/rectangular form.

Solution

Step 1: Evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex]

[latex]\scriptsize {{120}^\circ}[/latex] is not a special angle but [latex]\scriptsize {{180}^\circ}-{{120}^\circ}={{60}^\circ}[/latex] is a special angle. Therefore, we can evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex] without a calculator and transfer the angle into the correct quadrant, in this case, the second quadrant.

[latex]\scriptsize \cos {{60}^\circ}=\displaystyle \frac{1}{2}[/latex]
[latex]\scriptsize \sin {{60}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex]

Step 2: Find the standard form

We know that the complex number is in the second quadrant where cosine is negative and sine is positive.

[latex]\scriptsize \begin{align*}z &=4(\cos {{120}^\circ}+i\sin {{120}^\circ})\\ & =4\left( {-\displaystyle \frac{1}{2}+\displaystyle \frac{{\sqrt{3}}}{2}i} \right) && \text{Remember that cosine is negative in the }\\ &&&\text{second quadrant}\\ &=-2+\displaystyle \frac{{4\sqrt{3}}}{2}i\\ &=-2+2\sqrt{3}i\end{align*}[/latex]

The complex number in standard form is [latex]\scriptsize z=-2+2\sqrt{3}i[/latex].

Example 3.5

Convert [latex]\scriptsize z=3\text{cis4}{{\text{3}}^\circ}[/latex] into standard/rectangular form.

Solution

Step 1: Evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex]

[latex]\scriptsize {{43}^\circ}[/latex] is not a special angle. Therefore, we have to evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex] with a calculator. The complex number is in the first quadrant.

[latex]\scriptsize \cos {{43}^\circ}=0.7314[/latex]
[latex]\scriptsize \sin {{43}^\circ}=0.6820[/latex]

Step 2: Find the standard form

We know that the complex number is in the first quadrant where cosine and sine are both positive.

[latex]\scriptsize \displaystyle \begin{align*}z & =3(\cos {{43}^\circ}+i\sin {{43}^\circ})\\ & =3\left( {0.7314+0.6820i} \right)\\ & =2.9142+2.046i\end{align*}[/latex]

The complex number in standard form is [latex]\scriptsize z=2.9142+2.046i[/latex].

Exercise 3.2

Convert the following complex numbers into standard/rectangular form:

1. [latex]\scriptsize z=6\text{cis}{{45}^\circ}[/latex]
2. [latex]\scriptsize z=\sqrt{5}\text{cis21}{{\text{0}}^\circ}[/latex]
3. [latex]\scriptsize z=2\text{cis}{{40}^\circ}[/latex]

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to represent complex numbers in polar form.
• How to convert between standard/rectangular form and polar form.

Unit 3: Assessment

Suggested time to complete: 15 minutes

1. Represent the following in polar form:
   1. [latex]\scriptsize z=\sqrt{3}+1i[/latex]
   2. [latex]\scriptsize z=8-4i[/latex]
2. Represent the following in rectangular form:
   1. [latex]\scriptsize z=3\text{cis}{{240}^\circ}[/latex]
   2. [latex]\scriptsize z=7\text{cis}{{25}^\circ}[/latex]

The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

1. [latex]\scriptsize z=5-12i[/latex]
   Find [latex]\scriptsize r[/latex]:
   [latex]\scriptsize \begin{align*}r & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{5}^{2}}+{{{12}}^{2}}}}\\ & =\sqrt{{25+144}}\\ & =\sqrt{{169}}\\ & =13\end{align*}[/latex]
   Find [latex]\scriptsize \theta[/latex] ([latex]\scriptsize \theta[/latex] is in the fourth quadrant):
   [latex]\scriptsize \begin{align*}\cos \theta & =\displaystyle \frac{x}{r}=\displaystyle \frac{5}{{13}}\\\therefore \text{reference angle} & ={{67.38}^\circ}\\\therefore \theta & ={{360}^\circ}-{{67.38}^\circ}={{292.62}^\circ}\end{align*}[/latex]
   Polar form: [latex]\scriptsize z=13\text{cis}{{292.62}^\circ}[/latex]
2. [latex]\scriptsize z=-7+2i[/latex]
   Find [latex]\scriptsize r[/latex]:
   [latex]\scriptsize \begin{align*}r & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{{(-7)}}^{2}}+{{2}^{2}}}}\\& =\sqrt{{49+4}}\\ & =\sqrt{{53}}\end{align*}[/latex]
   Find [latex]\scriptsize \theta[/latex] ([latex]\scriptsize \theta[/latex] is in the second quadrant):
   [latex]\scriptsize \cos \theta =\displaystyle \frac{x}{r}=\displaystyle \frac{{-7}}{{\sqrt{{53}}}}[/latex]
   Work with [latex]\scriptsize \cos \theta =\displaystyle \frac{7}{{\sqrt{{53}}}}[/latex] to find a referance angle.
   [latex]\scriptsize \begin{align*}\therefore \text{reference angle} & ={{15.95}^\circ}\\\therefore \theta & ={{180}^\circ}-{{15.95}^\circ}={{164.05}^\circ}\end{align*}[/latex]
   Polar form: [latex]\scriptsize z=\sqrt{{53}}\text{cis164}\text{.0}{{\text{5}}^\circ}[/latex]

Back to Exercise 3.1

Exercise 3.2

1. [latex]\scriptsize z=6\text{cis}{{45}^\circ}[/latex]
   [latex]\scriptsize {{45}^\circ}[/latex] is a special angle and the complex number is in the first quadrant.
   [latex]\scriptsize \cos {{45}^\circ}=\displaystyle \frac{1}{{\sqrt{2}}}[/latex]
   [latex]\scriptsize \sin {{45}^\circ}=\displaystyle \frac{1}{{\sqrt{2}}}[/latex]
   [latex]\scriptsize \displaystyle \begin{align*}z & =6(\cos {{45}^\circ}+i\sin {{45}^\circ})\\ & =6\left( {\displaystyle \frac{1}{{\sqrt{2}}}+\displaystyle \frac{1}{{\sqrt{2}}}i} \right)\\ & =\displaystyle \frac{6}{{\sqrt{2}}}+\displaystyle \frac{6}{{\sqrt{2}}}i\end{align*}[/latex]
   The complex number in standard form is [latex]\scriptsize \displaystyle z=\displaystyle \frac{6}{{\sqrt{2}}}+\displaystyle \frac{6}{{\sqrt{2}}}i[/latex].
2. [latex]\scriptsize z=\sqrt{5}\text{cis21}{{\text{0}}^\circ}[/latex]
   [latex]\scriptsize {{180}^\circ}+{{30}^\circ}={{210}^\circ}[/latex]. Therefore, we use the special angle of [latex]\scriptsize {{30}^\circ}[/latex] in the third quadrant.
   [latex]\scriptsize \cos {{210}^\circ}=\cos ({{180}^\circ}+{{30}^\circ})=-\cos {{30}^\circ}=-\displaystyle \frac{{\sqrt{3}}}{2}[/latex]
   [latex]\scriptsize \sin {{210}^\circ}=\sin ({{180}^\circ}+{{30}^\circ})=-\sin {{30}^\circ}=-\displaystyle \frac{1}{2}[/latex]
   [latex]\scriptsize \displaystyle \begin{align*}z & =\sqrt{5}(\cos {{210}^\circ}+i\sin {{210}^\circ})\\ & =\sqrt{5}\left( {-\displaystyle \frac{{\sqrt{3}}}{2}-\displaystyle \frac{1}{2}i} \right)\quad \text{Both cosine and sine are negative in the third quadrant}\\ & =-\displaystyle \frac{{\sqrt{{15}}}}{2}-\displaystyle \frac{{\sqrt{5}}}{2}i\end{align*}[/latex]
   The complex number in standard form is [latex]\scriptsize \displaystyle z=-\displaystyle \frac{{\sqrt{{15}}}}{2}-\displaystyle \frac{{\sqrt{5}}}{2}i[/latex].
3. [latex]\scriptsize z=2\text{cis}{{40}^\circ}[/latex]
   [latex]\scriptsize {{40}^\circ}[/latex] is not a special angle. The complex number is in the first quadrant.
   [latex]\scriptsize \cos {{40}^\circ}=0.7660[/latex]
   [latex]\scriptsize \sin {{40}^\circ}=0.6428[/latex]
   [latex]\scriptsize \displaystyle \begin{align*}z & =2(\cos {{40}^\circ}+i\sin {{40}^\circ})\\ & =2\left( {0.7660+0.6428i} \right)\quad \text{Both cosine and sine are positive in the first quadrant}\\ & =1.532+1.2856i\end{align*}[/latex]
   The complex number in standard form is [latex]\scriptsize \displaystyle z=1.532+1.2856i[/latex].

Back to Exercise 3.2

Unit 3: Assessment

1. .
   1. [latex]\scriptsize z=\sqrt{3}+1i[/latex]
      Find [latex]\scriptsize r[/latex]:
      [latex]\scriptsize \begin{align*}r & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{{\left( {\sqrt{3}} \right)}}^{2}}+{{1}^{2}}}}\\ & =\sqrt{{3+1}}\\ & =2\end{align*}[/latex]
      Find [latex]\scriptsize \theta[/latex]:
      The complex number is in the first quadrant.
      [latex]\scriptsize \begin{align*}\cos \theta & =\displaystyle \frac{x}{r}=\displaystyle \frac{{\sqrt{3}}}{2}\\\therefore \theta & ={{30}^\circ}\end{align*}[/latex]
      Polar form: [latex]\scriptsize z=2\text{cis}{{30}^\circ}[/latex]
   2. [latex]\scriptsize z=8-4i[/latex]
      Find [latex]\scriptsize r[/latex]:
      [latex]\scriptsize \begin{align*}r & =\sqrt{{{{x}^{2}}+{{y}^{2}}}}\\ & =\sqrt{{{{8}^{2}}+{{{(-4)}}^{2}}}}\\ & =\sqrt{{64+16}}\\ & =\sqrt{{80}}\\ & =4\sqrt{5}\end{align*}[/latex]
      Find [latex]\scriptsize \theta[/latex]:
      The complex number is in the fourth quadrant.
      [latex]\scriptsize \begin{align*}\cos \theta & =\displaystyle \frac{x}{r}=\displaystyle \frac{8}{{4\sqrt{5}}}=\displaystyle \frac{2}{{\sqrt{5}}}\\\therefore \text{Reference angle} & ={{26.57}^\circ}\\\therefore \theta & ={{360}^\circ}-{{26.57}^\circ}={{333.43}^\circ}\end{align*}[/latex]
      Polar form: [latex]\scriptsize z=4\sqrt{5}\text{cis}{{333.43}^\circ}[/latex]
2. .
   1. [latex]\scriptsize z=3\text{cis}{{240}^\circ}[/latex]
      [latex]\scriptsize {{240}^\circ}[/latex] is not a special angle but [latex]\scriptsize {{240}^\circ}-{{180}^\circ}={{60}^\circ}[/latex] is a special angle. Therefore, we can evaluate [latex]\scriptsize \cos \theta[/latex] and [latex]\scriptsize \sin \theta[/latex] without a calculator and transfer the angle into the correct quadrant, in this case, the third quadrant.
      [latex]\scriptsize \cos {{60}^\circ}=\displaystyle \frac{1}{2}[/latex]
      [latex]\scriptsize \sin {{60}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex]
      The complex number is in the third quadrant where cosine and sine are both negative.
      [latex]\scriptsize \displaystyle \begin{align*}z & =3(\cos {{240}^\circ}+i\sin {{240}^\circ})\\ & =3\left( {-\displaystyle \frac{1}{2}-\displaystyle \frac{{\sqrt{3}}}{2}i} \right)\quad \text{cosine and sine are negative in the third quadrant}\\ & =-\displaystyle \frac{3}{2}-\displaystyle \frac{{3\sqrt{3}}}{2}i\end{align*}[/latex]
      Standard form is [latex]\scriptsize z=-\displaystyle \frac{3}{2}-\displaystyle \frac{{3\sqrt{3}}}{2}i[/latex].
   2. [latex]\scriptsize z=7\text{cis}{{25}^\circ}[/latex]
      [latex]\scriptsize {{25}^\circ}[/latex] is not a special angle. The complex number is in the first quadrant.
      [latex]\scriptsize \cos {{25}^\circ}=0.9063[/latex]
      [latex]\scriptsize \sin {{25}^\circ}=0.4226[/latex]The complex number is in the first quadrant where cosine and sine are positive.
      [latex]\scriptsize \displaystyle \begin{align*}z & =7(\cos {{25}^\circ}+i\sin {{25}^\circ})\\ & =7\left( {0.9063+0.4226i} \right)\quad \text{cosine and sine are positive in the first quadrant}\\ & =6.3441+2.9582i\end{align*}[/latex]
      Standard form is [latex]\scriptsize z=6.3441+2.9582i[/latex].

Back to Unit 3: Assessment