Space, shape and measurement: Solve problems by constructing and interpreting trigonometric models
Unit 2: Use reduction formulae to simplify trig ratios
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Apply reduction formulae for function values of [latex]\scriptsize ({{90}^\circ}\pm \theta )[/latex].
- Apply reduction formulae for function values of [latex]\scriptsize ({{180}^\circ}\pm \theta )[/latex].
- Apply reduction formulae for function values of [latex]\scriptsize ({{360}^\circ}\pm \theta )[/latex].
- Simplify trigonometric ratios involving any combination of reduction formulae.
What you should know
Before you start this unit, make sure you can:
- Define the three basic trigonometric ratios of sine, cosine and tangent.
- Use the CAST diagram to determine in which quadrants the three trigonometric ratios are positive or negative.
Introduction
We have said many times that one of the unique properties of the trigonometric functions is that they are periodic. They repeat themselves. We know that the period of the sine and cosine functions are [latex]\scriptsize {{360}^\circ}[/latex] and the period of the tangent function is [latex]\scriptsize {{180}^\circ}[/latex].
A good way to understand why the trig functions are periodic is to consider the unit circle, something we have done on numerous occasions. Each time we complete one revolution of the unit circle, we are basically starting at [latex]\scriptsize {{0}^\circ}[/latex] again and so the behaviour of the trig functions simply repeat themselves.
If you need a reminder of this and have an internet connection, then spend some time playing with the following interactive simulations for the sine and cosine functions. In each case, you will find a slider that will allow you to change the angle between [latex]\scriptsize -{{720}^\circ}[/latex] and [latex]\scriptsize {{720}^\circ}[/latex].
For each function, remind yourself how the point on the unit circle, as the angle with the positive x-axis changes, produces the function’s graph in each case. Also note how the functions repeat themselves every [latex]\scriptsize {{360}^\circ}[/latex].
One of the consequences of this periodicity is that there are specific rules we can use to reduce the trig ratios of angles greater than [latex]\scriptsize {{90}^\circ}[/latex] to their equivalents with angles between [latex]\scriptsize {{0}^\circ}[/latex] and [latex]\scriptsize {{90}^\circ}[/latex].
Reduce sine, cosine and tangent
Let’s begin by investigating how we can reduce the sine of angles in the second, third and fourth quadrants to their equivalent acute or first quadrant ratios.
Activity 2.1: Reduce sine
Time required: 20 minutes
What you need:
- an internet connection
What to do:
For this activity, you will need a working Internet connection.
- Open this interactive sine function simulation with a slider to change the angle from [latex]\scriptsize {{0}^\circ}[/latex] to [latex]\scriptsize {{360}^\circ}[/latex]If you have access to the internet, visit this interactive simulation.
As you change the angle, you can see that the angles in the unit circle and on the graph change. You will also notice that the angles within each of the four unit circle quadrants have also been marked on the graph. - Move the slider slowly from [latex]\scriptsize {{0}^\circ}[/latex] to [latex]\scriptsize {{180}^\circ}[/latex] and notice each time the function value is [latex]\scriptsize 0.5[/latex]. From unit 1 you should already know what angle results in a sine ratio of [latex]\scriptsize \displaystyle \frac{1}{2}[/latex].
- When [latex]\scriptsize \sin \theta =\displaystyle \frac{1}{2}[/latex] in the second quadrant, what angle does the radius of the unit circle make with the positive x-axis? What angle does it make with the negative x-axis? What is the relationship between these two angles?
- What can you say about the values of [latex]\scriptsize \sin {{30}^\circ}[/latex] and [latex]\scriptsize \sin {{150}^\circ}[/latex]?
- Does this relationship hold for other angles in the first and second quadrants? What value of [latex]\scriptsize \theta[/latex] in the second quadrant gives the same value as [latex]\scriptsize \sin {{45}^\circ}[/latex]? What value of [latex]\scriptsize \theta[/latex] in the second quadrant gives the same value as [latex]\scriptsize \sin {{60}^\circ}[/latex]? What is the size of the angle between the radius and the negative x-axis in each case?
- Can you write a general expression for this relationship that is true for any angle for [latex]\scriptsize {{0}^\circ}\le \theta \le {{90}^\circ}[/latex]?
- Now continue to move the slider into the third and fourth quadrants. What angles result in a function value of [latex]\scriptsize \sin \theta =-\displaystyle \frac{1}{2}[/latex]?
- What can you say about the values of [latex]\scriptsize \sin {{30}^\circ}[/latex] and [latex]\scriptsize \sin {{210}^\circ}[/latex] and [latex]\scriptsize \sin {{330}^\circ}[/latex]?
- Can you write general rules for these relationships that are true for [latex]\scriptsize {{0}^\circ}\le \theta \le {{90}^\circ}[/latex] that are similar to the one you wrote in response to question 6? In each case, think about what angle the radius of the unit circle makes with the negative and positive x-axis respectively?
What did you find?
- The interactive simulation at the link provided is shown in Figure 1.
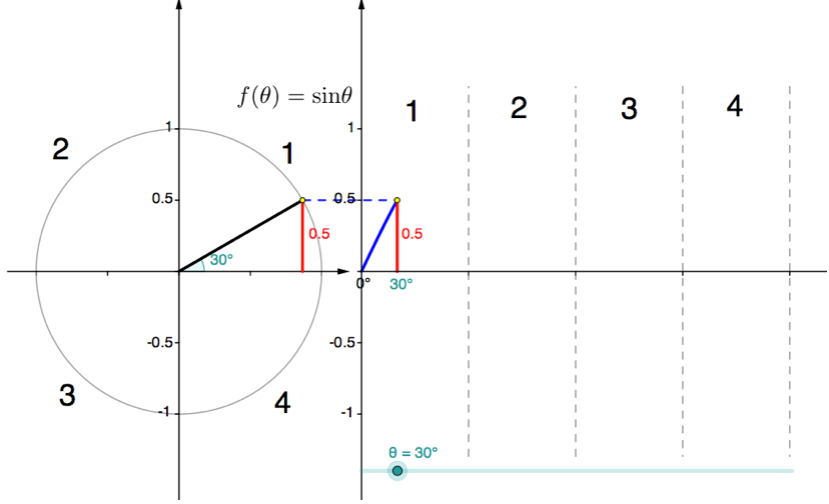
Figure 1: Interactive sine function simulation - [latex]\scriptsize \sin \theta =\displaystyle \frac{1}{2}[/latex] at two angles: [latex]\scriptsize {{30}^\circ}[/latex] (see Figure 1) and [latex]\scriptsize {{150}^\circ}[/latex] (see Figure 2).
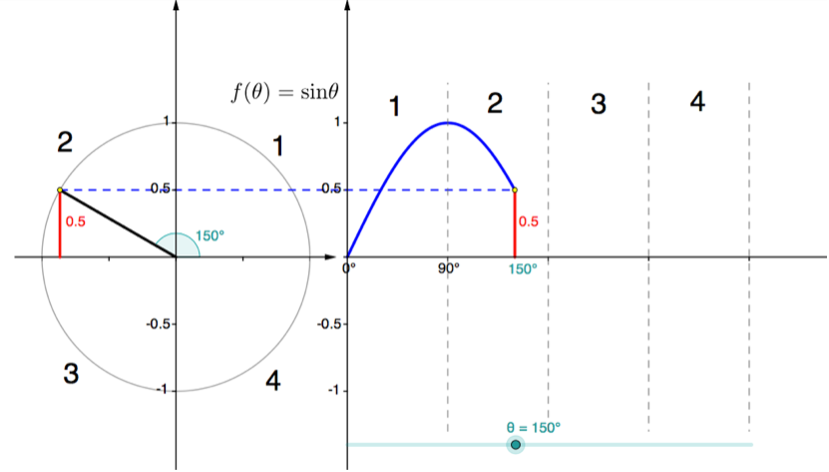
Figure 2: [latex]\scriptsize \sin {{150}^\circ}=\displaystyle \frac{1}{2}[/latex] - The radius makes an angle of [latex]\scriptsize {{150}^\circ}[/latex] with the positive x-axis but an angle of [latex]\scriptsize {{30}^\circ}[/latex] with the negative x-axis. Therefore, the angle made with the negative x-axis is [latex]\scriptsize {{180}^\circ}-{{150}^\circ}={{30}^\circ}[/latex].
- [latex]\scriptsize \sin {{30}^\circ}=\sin {{150}^\circ}=0.5[/latex]
- [latex]\scriptsize \sin {{45}^\circ}=\sin {{135}^\circ}[/latex](see Figure 3). The size of the angle between the radius and negative x-axis is [latex]\scriptsize {{45}^\circ}[/latex].
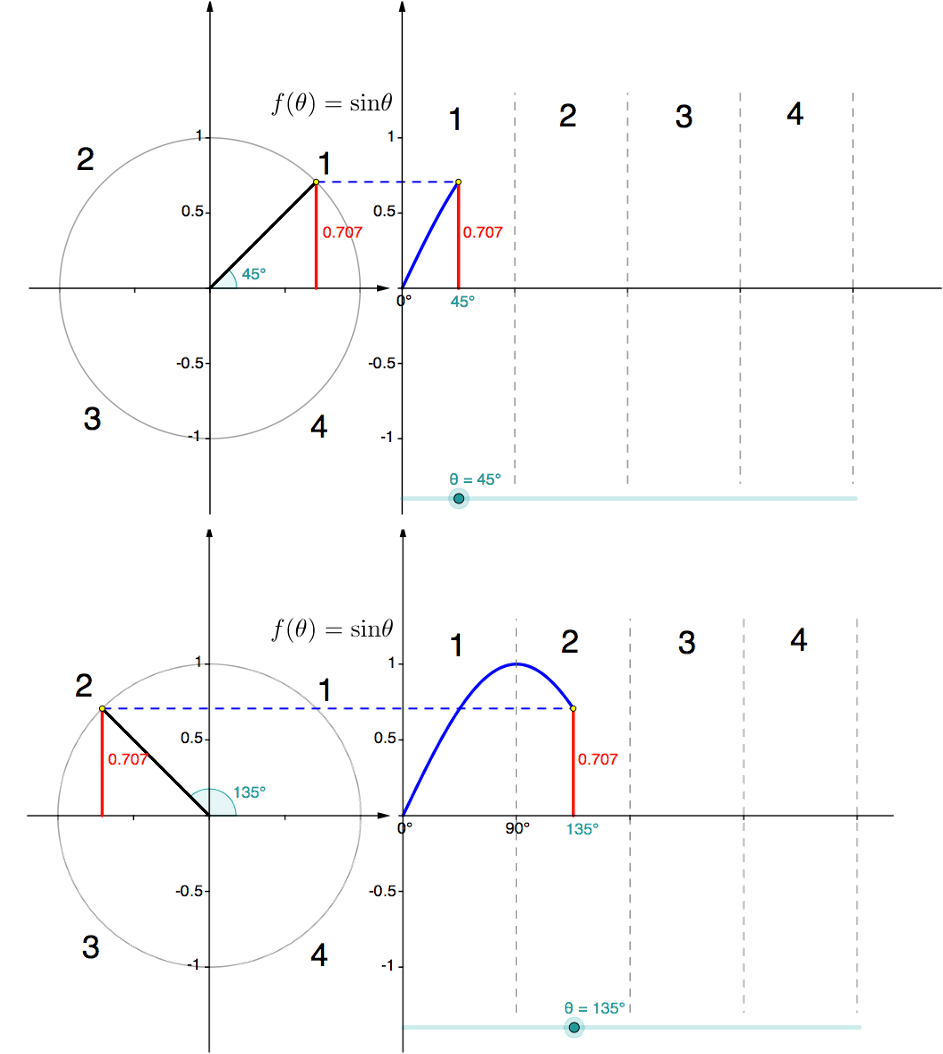
Figure 3: [latex]\scriptsize \sin {{45}^\circ}=\sin {{135}^\circ}[/latex] [latex]\scriptsize \sin {{60}^\circ}=\sin {{120}^\circ}[/latex] (see Figure 4). The size of the angle between the radius and negative x-axis is [latex]\scriptsize {{60}^\circ}[/latex].
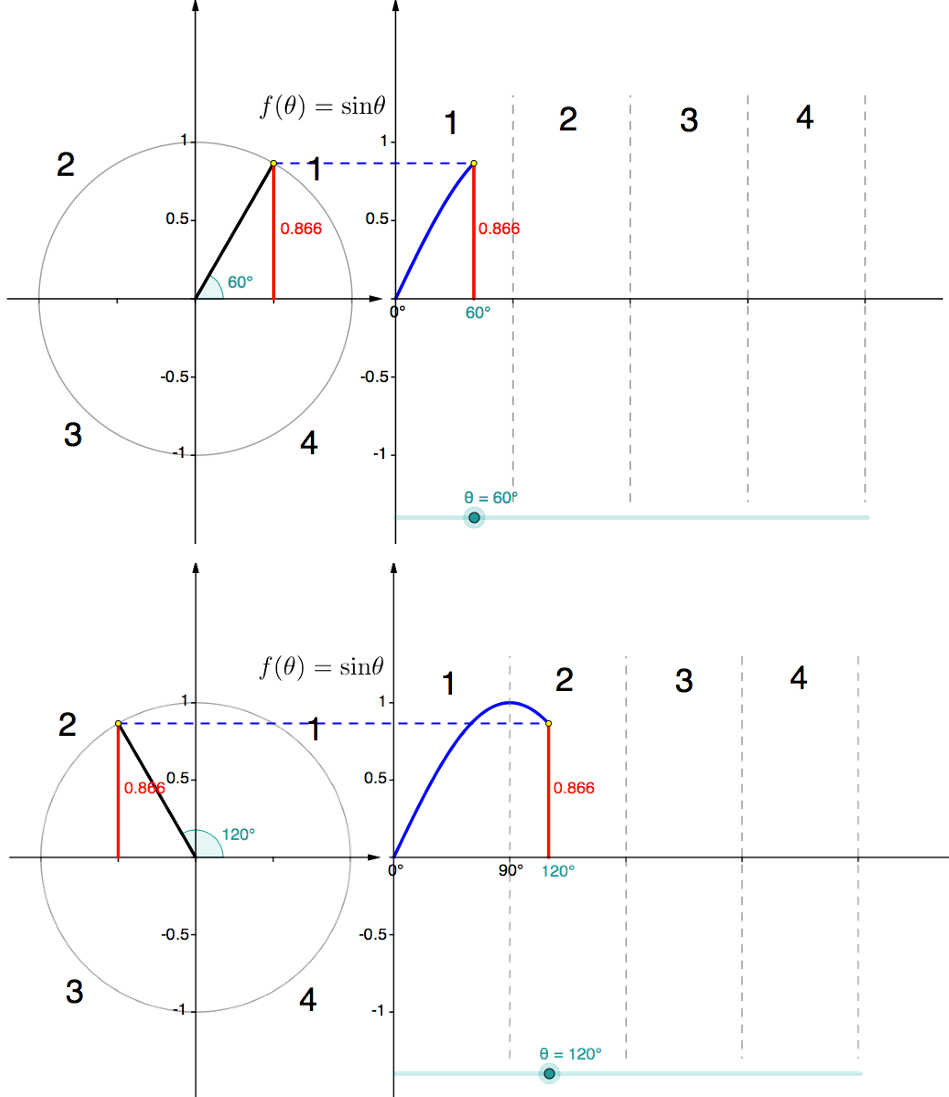
Figure 4: [latex]\scriptsize \sin {{60}^\circ}=\sin {{120}^\circ}[/latex] - [latex]\scriptsize \sin \theta =\sin ({{180}^\circ}-\theta )[/latex]
- [latex]\scriptsize \sin {{210}^\circ}=-\displaystyle \frac{1}{2}[/latex] and [latex]\scriptsize \sin {{330}^\circ}=-\displaystyle \frac{1}{2}[/latex]
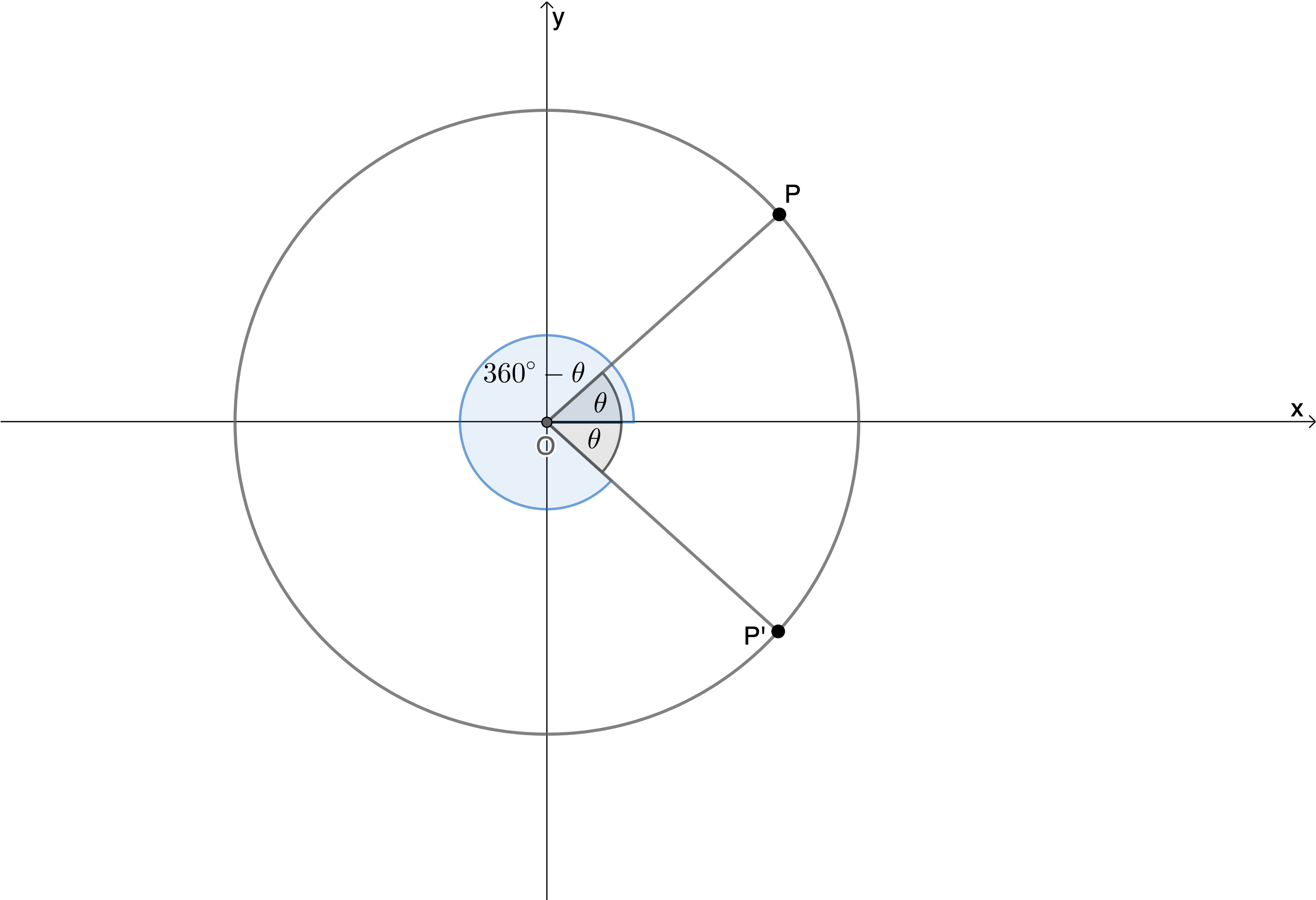
- [latex]\scriptsize \sin {{30}^\circ}=-\sin {{210}^\circ}[/latex] or [latex]\scriptsize -\sin {{30}^\circ}=\sin {{210}^\circ}[/latex] (see Figure 5)
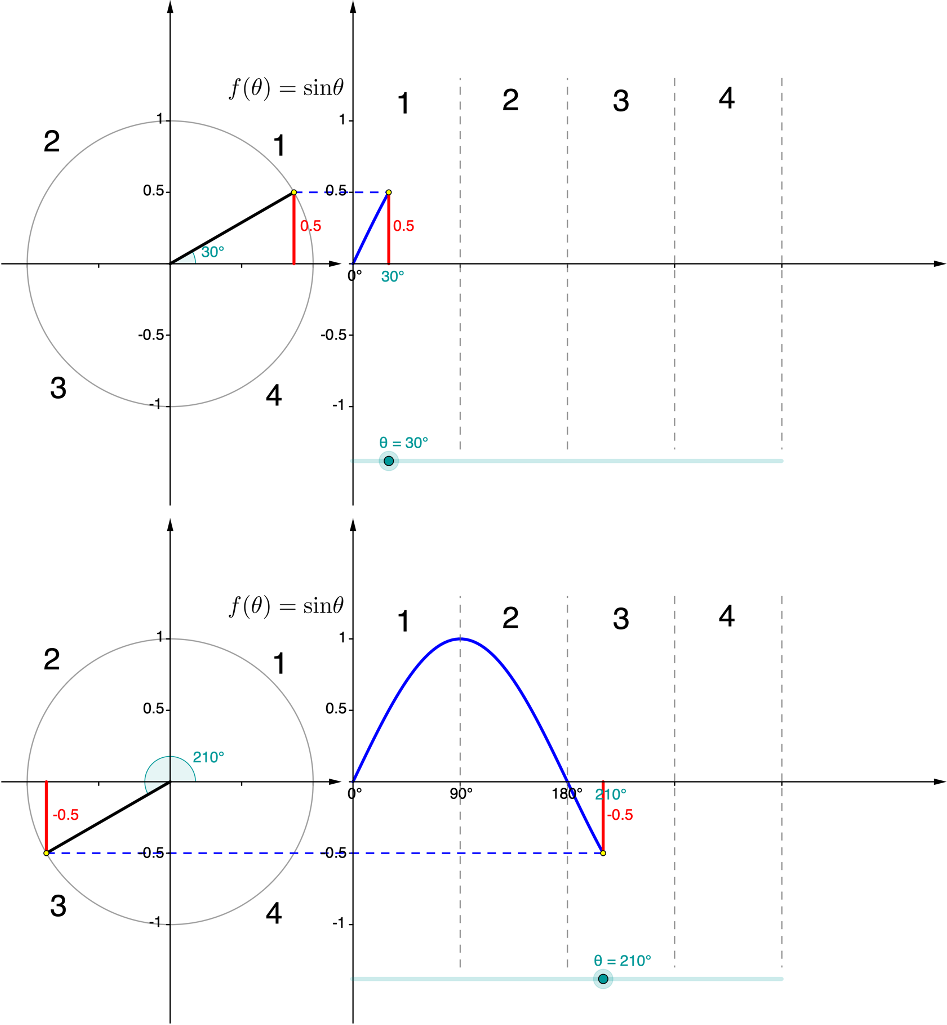
Figure 5: [latex]\scriptsize \sin {{30}^\circ}=-\sin {{210}^\circ}[/latex] or [latex]\scriptsize -\sin {{30}^\circ}=\sin {{210}^\circ}[/latex] [latex]\scriptsize \sin {{30}^\circ}=-\sin {{330}^\circ}[/latex] or [latex]\scriptsize -\sin {{30}^\circ}=\sin {{330}^\circ}[/latex] (see Figure 6)
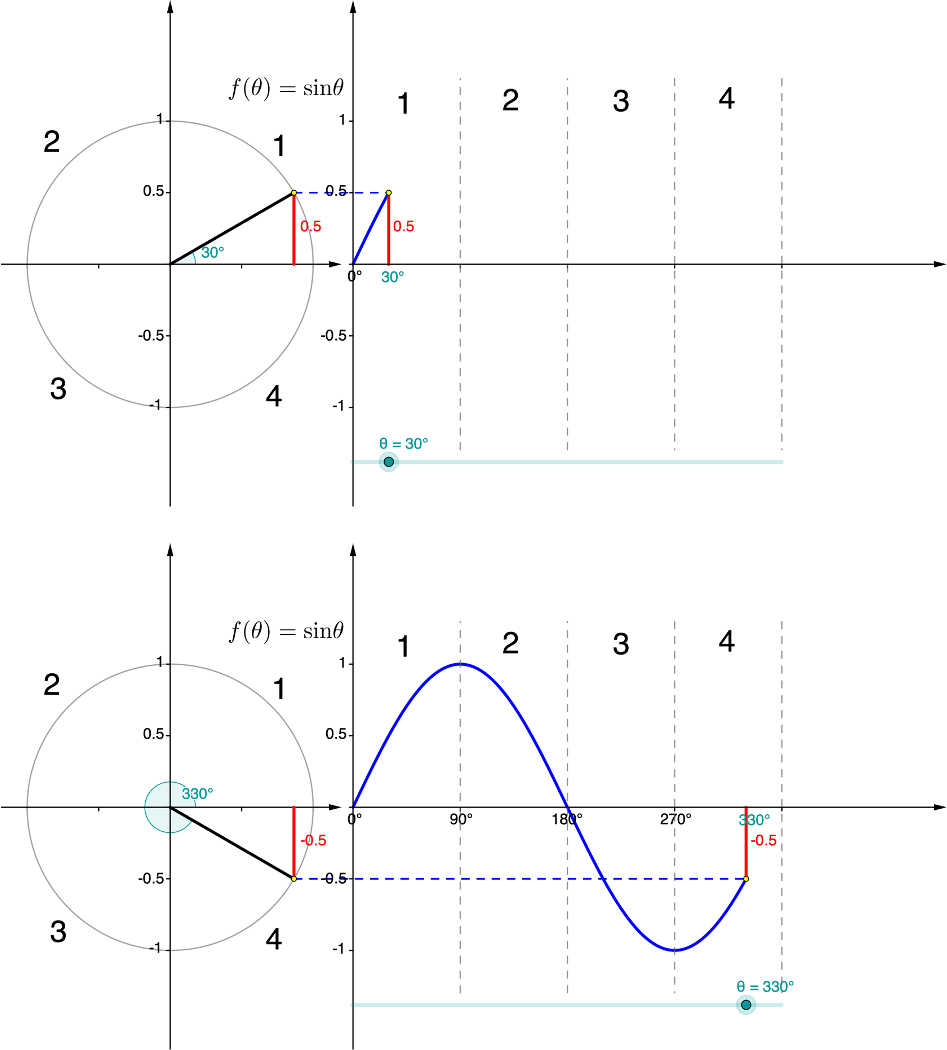
Figure 6: [latex]\scriptsize \sin {{30}^\circ}=-\sin {{330}^\circ}[/latex] or [latex]\scriptsize -\sin {{30}^\circ}=\sin {{330}^\circ}[/latex] - [latex]\scriptsize \sin \theta =-\sin ({{180}^\circ}+\theta )[/latex] or
[latex]\scriptsize \sin \theta =-\sin ({{360}^\circ}-\theta )[/latex] or [latex]\scriptsize \sin \theta =-\sin (-\theta )[/latex]
We have ways to rewrite the sine of angles that are between [latex]\scriptsize {{90}^\circ}[/latex] and [latex]\scriptsize {{360}^\circ}[/latex] (angles that are in the second, third or fourth quadrants) in terms of the equivalent ratio of an acute angle in the first quadrant.
We saw that:
- [latex]\scriptsize \sin \theta =\sin ({{180}^\circ}-\theta )[/latex] ̶ the graph shows that sine is positive in the first and second quadrants.
- [latex]\scriptsize \sin \theta =-\sin ({{180}^\circ}+\theta )[/latex] ̶ the graph shows that that sine is negative in the third quadrant, hence we need the negative sign.
- [latex]\scriptsize \sin \theta =-\sin ({{360}^\circ}-\theta )[/latex] or [latex]\scriptsize \sin \theta =-\sin (-\theta )[/latex] ̶ the graph shows that sine is negative in the fourth quadrant, hence we need the negative sign. We can write the acute angle in the fourth quadrant either as [latex]\scriptsize ({{360}^\circ}-\theta )[/latex] or just [latex]\scriptsize (-\theta )[/latex].
Reduction rules for sine:
[latex]\scriptsize \sin ({{180}^\circ}-\theta )=\sin \theta[/latex]
[latex]\scriptsize \sin ({{180}^\circ}+\theta )=-\sin \theta[/latex]
[latex]\scriptsize \sin ({{360}^\circ}-\theta )=-\sin \theta[/latex] or [latex]\scriptsize \sin (-\theta )=-\sin \theta[/latex]
The same kind of reduction rules exist for the cosine and tangent functions. If you have an internet connection, satisfy yourself that this is true by exploring the cosine function simulation.
If you have access to the internet, visit this interactive simulation.
While you explore, see if you can write down the same set of reduction rules as above but this time for cosine. Pay careful attention to the quadrants in which cosine is negative and positive.
Reduction rules for cosine:
- [latex]\scriptsize \cos ({{180}^\circ}-\theta )=-\cos \theta[/latex]
- [latex]\scriptsize \cos ({{180}^\circ}+\theta )=-\cos \theta[/latex]
- [latex]\scriptsize \cos ({{360}^\circ}-\theta )=\cos \theta[/latex] or [latex]\scriptsize \cos (-\theta )=\cos \theta[/latex]
Can you write the same set of reduction rules for tangent? If you have an internet connection have a look at and the tangent function simulation.
f you have access to the internet, visit this interactive simulation.
Pay careful attention to the quadrants in which tangent is negative and positive.
Reduction rules for tangent:
- [latex]\scriptsize \tan ({{180}^\circ}-\theta )=-\tan \theta[/latex]
- [latex]\scriptsize \tan ({{180}^\circ}+\theta )=\tan \theta[/latex]
- [latex]\scriptsize \tan ({{360}^\circ}-\theta )=-\tan \theta[/latex] or [latex]\scriptsize \tan (-\theta )=-\tan \theta[/latex]
Example 2.1
Simplify the following trig ratios to ratios of an acute angle:
- [latex]\scriptsize \sin {{300}^\circ}[/latex]
- [latex]\scriptsize \cos {{213}^\circ}[/latex]
- [latex]\scriptsize \tan {{117}^\circ}[/latex]
Solution
- .
[latex]\scriptsize \begin{align*}\sin 300^\circ&=\sin(360^\circ=60^\circ)\\ &=-\sin60^\circ &&300^\circ\text{ is in the fourth quadrant where sin in negative}\\\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\cos {{213}^\circ}&=\cos ({{180}^\circ}+{{33}^\circ})\\&=-\cos {{33}^\circ}&&{{213}^\circ}\text{ is in the third quadrant where cosine is negative}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\tan {{117}^\circ}&=\tan ({{180}^\circ}-{{63}^\circ})\\&=-\tan {{63}^\circ}&&{{117}^\circ}\text{ is in the second quadrant where tangent is negative}\end{align*}[/latex]
Example 2.2
Simplify the following to ratios of an acute angle:
[latex]\scriptsize \displaystyle \frac{{\sin {{{163}}^\circ}}}{{\cos {{{197}}^\circ}}}+\tan {{17}^\circ}[/latex]
Solution
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin {{{163}}^\circ}}}{{\cos {{{197}}^\circ}}}+\tan {{17}^\circ}&=\displaystyle \frac{{\sin ({{{180}}^\circ}-{{{17}}^\circ})}}{{\cos ({{{180}}^\circ}+{{{17}}^\circ})}}+\tan {{17}^\circ}\\&=\displaystyle \frac{{\sin {{{17}}^\circ}}}{{-\cos {{{17}}^\circ}}}+\tan {{17}^\circ}\end{align*}[/latex]
Example 2.3
Determine the value of the following expression without a calculator:
[latex]\scriptsize \tan {{150}^\circ}\sin {{210}^\circ}-\cos {{210}^\circ}[/latex]
Solution
Remember that ‘without a calculator’ means that you are expected to use special angles.
[latex]\scriptsize \begin{align*}\tan {{150}^\circ}\sin {{210}^\circ}-\cos {{210}^\circ}&=\tan ({{180}^\circ}-{{30}^\circ})\sin ({{180}^\circ}+{{30}^\circ})-\cos ({{180}^\circ}+{{30}^\circ})\\& \text{Write each of the angles with a special angle}\\&=(-\tan {{30}^\circ})(-\sin {{30}^\circ})-(-\cos {{30}^\circ})\\& \text{Apply the reduction rules being careful about signs}\\&=\left( {-\displaystyle \frac{1}{{\sqrt{3}}}} \right)\times \left( {-\displaystyle \frac{1}{2}} \right)+\displaystyle \frac{{\sqrt{3}}}{2}\\&=\displaystyle \frac{1}{{2\sqrt{3}}}+\displaystyle \frac{{\sqrt{3}}}{2}\\&=\displaystyle \frac{{1+\sqrt{3}}}{{2\sqrt{3}}}\\&=\displaystyle \frac{{1+\sqrt{3}}}{{2\sqrt{3}}}\times \displaystyle \frac{{\sqrt{3}}}{{\sqrt{3}}}\\&=\displaystyle \frac{{\sqrt{3}+3}}{6}\end{align*}[/latex]
Exercise 2.1
- Simplify the following to ratios of an acute angle:
- [latex]\scriptsize \cos {{257}^\circ}[/latex]
- [latex]\scriptsize \tan {{198}^\circ}[/latex]
- [latex]\scriptsize \tan {{162}^\circ}[/latex]
- [latex]\scriptsize \tan (-{{18}^\circ})[/latex]
- [latex]\scriptsize \sin {{241}^\circ}[/latex]
- [latex]\scriptsize \displaystyle \frac{{\sin {{{67}}^\circ}}}{{\tan {{{293}}^\circ}}}+\cos {{113}^\circ}[/latex]
- Determine the value of the following expressions without a calculator:
- [latex]\scriptsize \displaystyle \frac{{{{{\tan }}^{2}}{{{225}}^\circ}-\sin (-{{{30}}^\circ})\cos (-{{{30}}^\circ})}}{{\tan {{{300}}^\circ}}}[/latex]
- [latex]\scriptsize {{\left( {\displaystyle \frac{{\sin {{{210}}^\circ}}}{{\cos {{{210}}^\circ}}}} \right)}^{2}}+2\tan {{210}^\circ}[/latex]
The full solutions are at the end of the unit.
Co-function reductions
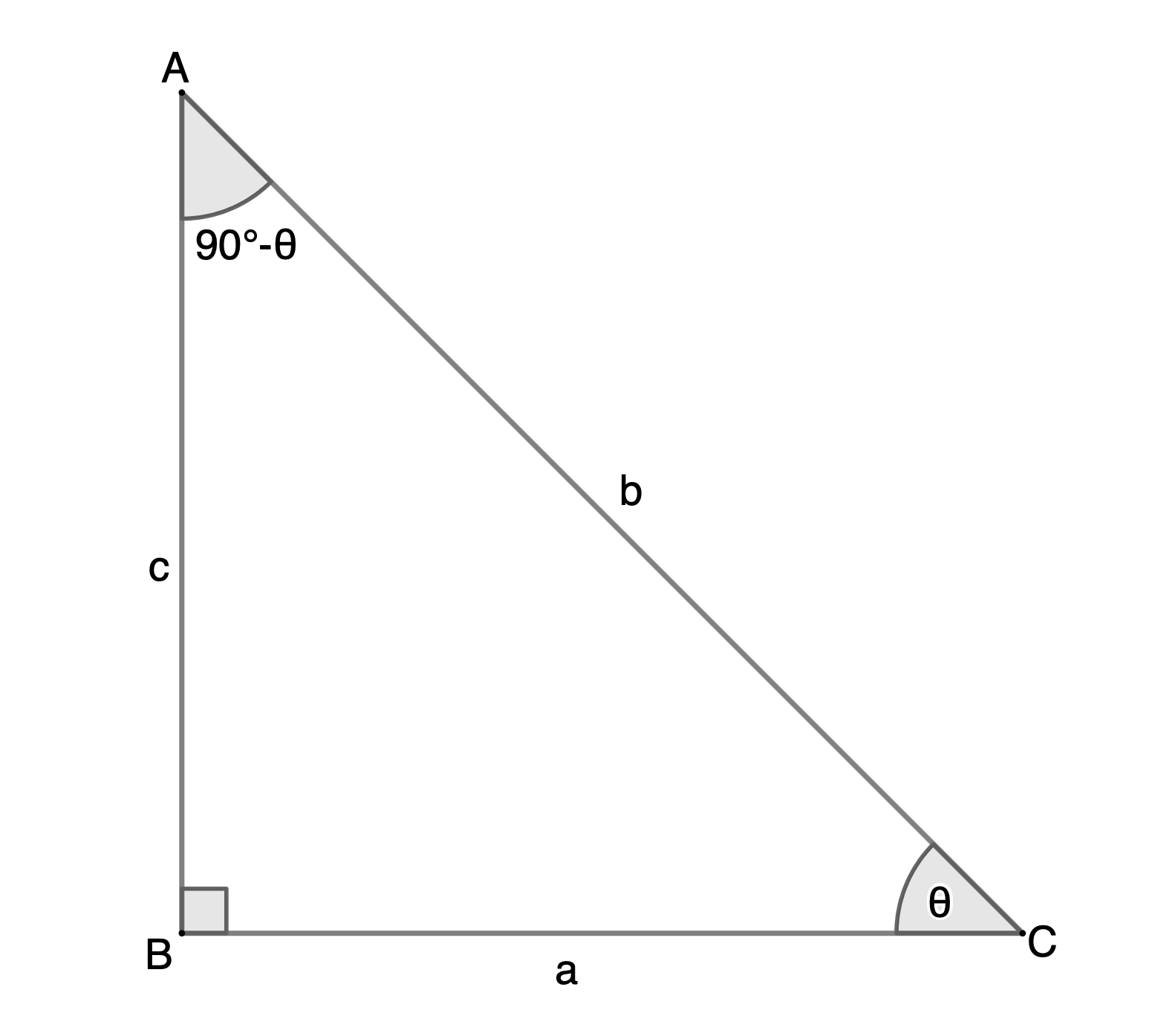
In unit 1 you might have noticed that [latex]\scriptsize \sin {{30}^\circ}=\displaystyle \frac{1}{2}=\cos {{60}^\circ}[/latex] and that [latex]\scriptsize \sin {{45}^\circ}=\displaystyle \frac{1}{{\sqrt{2}}}=\cos {{45}^\circ}[/latex]. Can you see a pattern? Can you write a general rule for this relationship between sine and cosine in any right-angled triangle?
We can see from Figure 7 that if the angle at [latex]\scriptsize C[/latex] is [latex]\scriptsize \theta[/latex], then the angle at [latex]\scriptsize A[/latex] must be [latex]\scriptsize ({{90}^\circ}-\theta )[/latex] (the angles inside a triangle are supplementary). Therefore, if [latex]\scriptsize \sin \theta =\displaystyle \frac{c}{b}[/latex], [latex]\scriptsize \cos ({{90}^\circ}-\theta )=\displaystyle \frac{c}{b}[/latex] and [latex]\scriptsize \sin \theta =\cos ({{90}^\circ}-\theta )[/latex]. Also, [latex]\scriptsize \cos \theta =\sin ({{90}^\circ}-\theta )[/latex].
On the Cartesian plane, we can see that the angles [latex]\scriptsize \theta[/latex] and [latex]\scriptsize {{90}^\circ}-\theta[/latex] create two identical triangles such that [latex]\scriptsize \sin \theta =\cos ({{90}^\circ}-\theta )[/latex] and [latex]\scriptsize \cos \theta =\sin ({{90}^\circ}-\theta )[/latex] (see Figure 8).
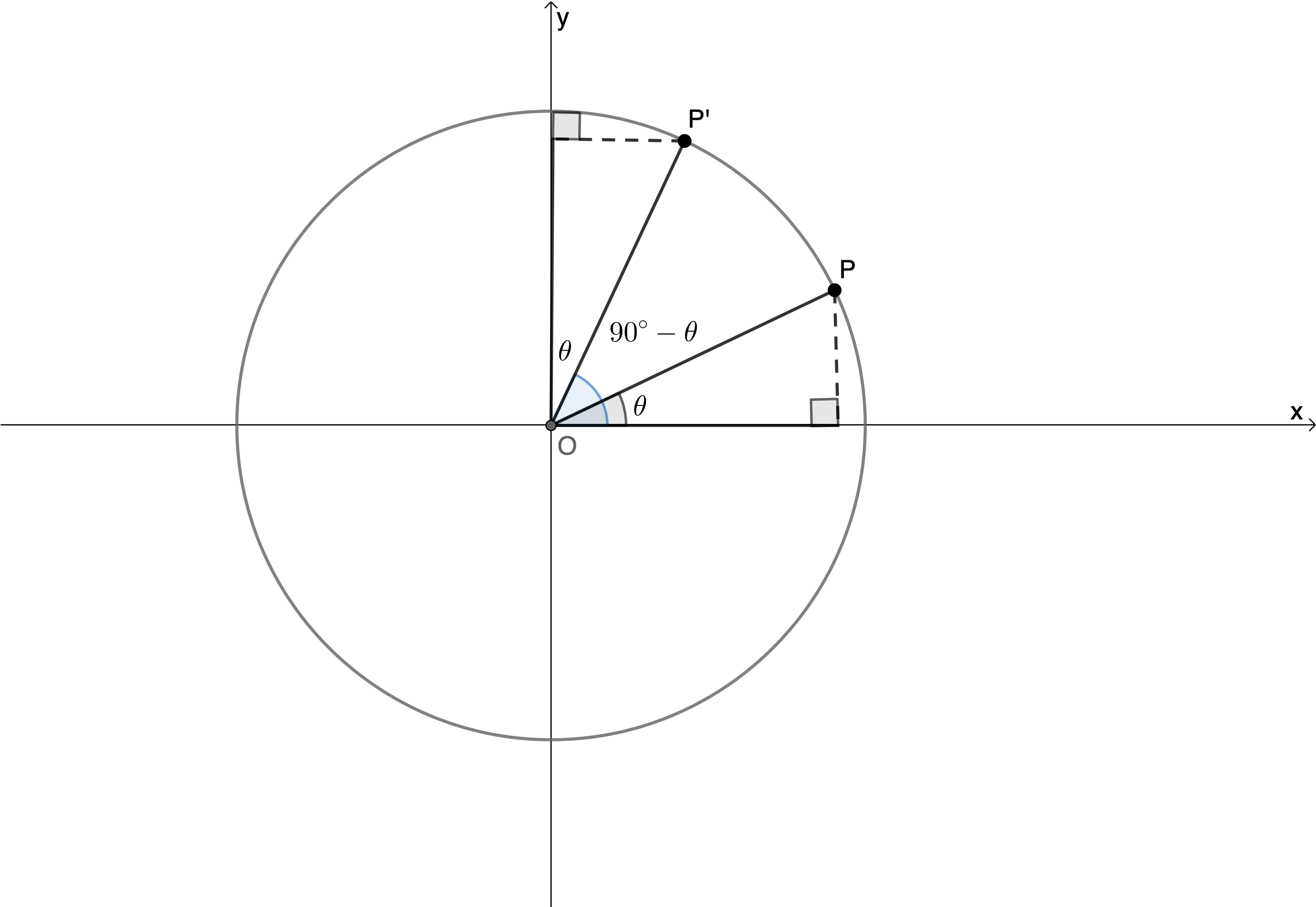
Because of this relationship, we say that sine and cosine are co-functions. This is why cosine is called cosine. It is the co-function of sine!
Did you know?
The co-function of tangent is called cotangent or cot for short. If [latex]\scriptsize \tan \theta =\displaystyle \frac{y}{x}[/latex] then [latex]\scriptsize \cot \theta =\displaystyle \frac{x}{y}[/latex]. In other words, [latex]\scriptsize \cot \theta =\displaystyle \frac{1}{{\tan \theta }}[/latex]. The cotangent function is not part of the NC(V) level 3 curriculum.
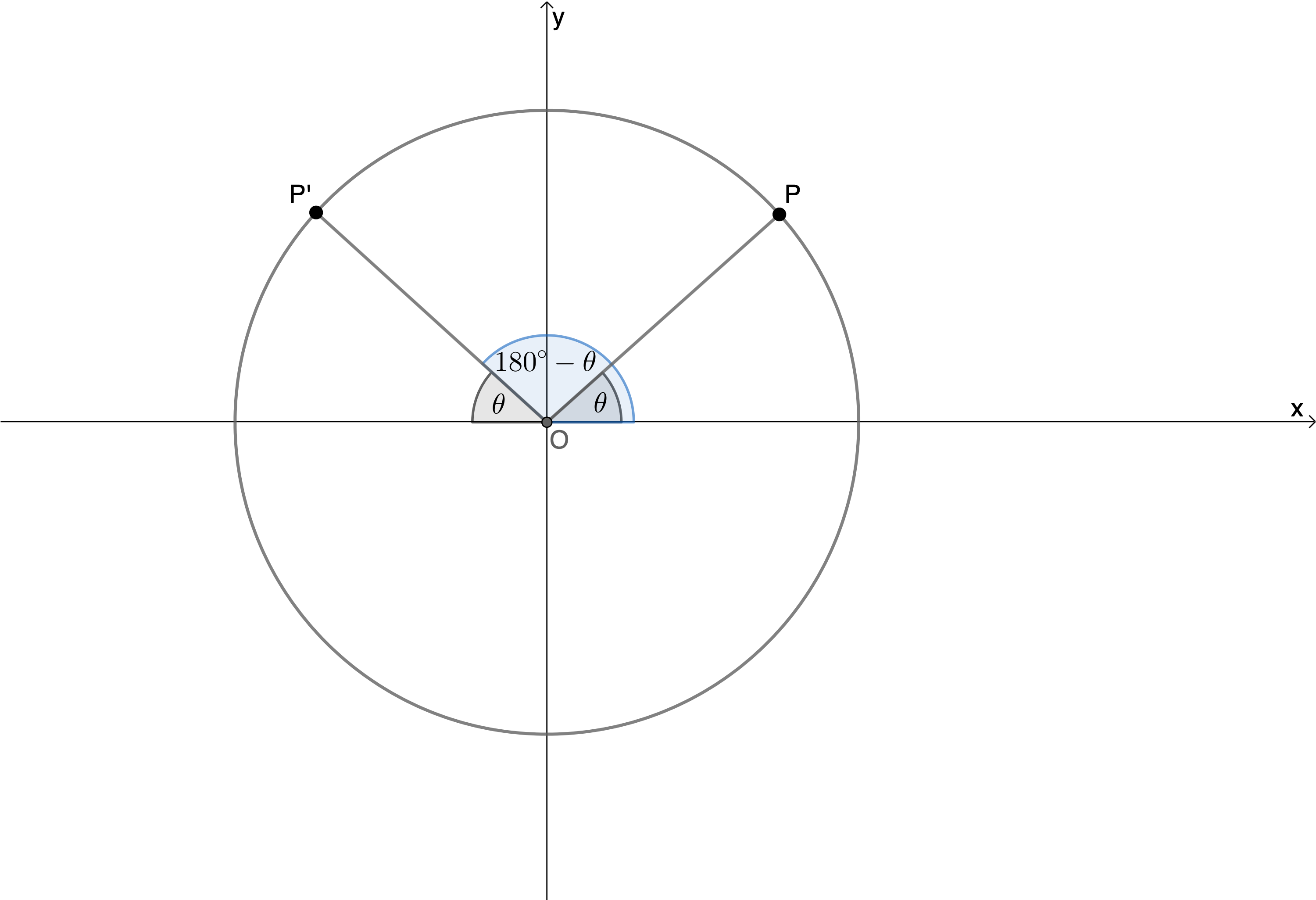
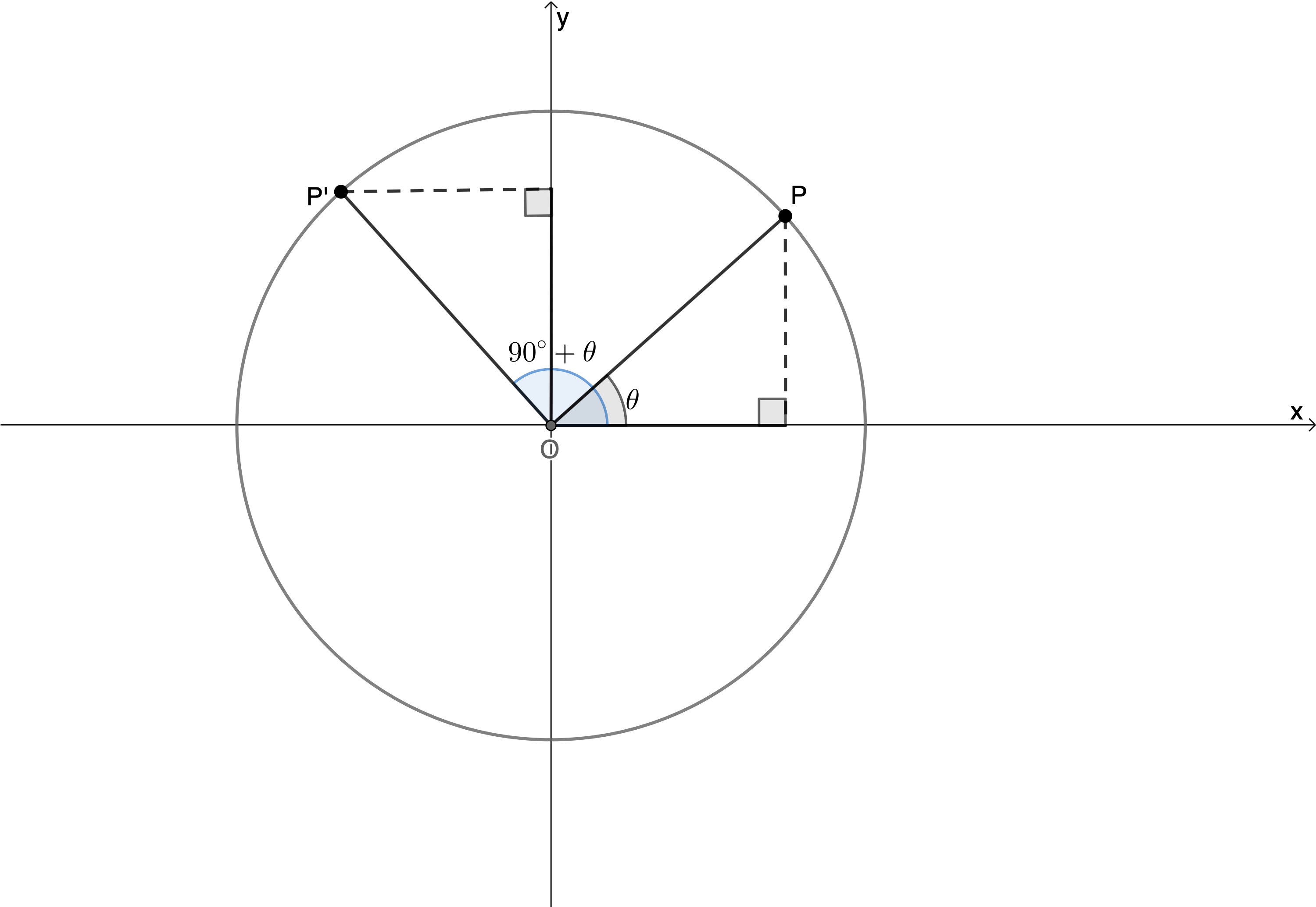
Does this relationship between sine and cosine extend outside the first quadrant? In other words, is [latex]\scriptsize \sin ({{90}^\circ}+\theta )=\cos \theta[/latex]? Have a look at Figure 9.
Here we can see that [latex]\scriptsize \theta[/latex] and [latex]\scriptsize {{90}^\circ}+\theta[/latex] create two identical triangles such that [latex]\scriptsize \sin ({{90}^\circ}+\theta )=\cos \theta[/latex] and [latex]\scriptsize \cos ({{90}^\circ}+\theta )=-\sin \theta[/latex] . Notice that the distance P from the y-axis is a negative value on the x-axis, so cosine is negative in the second quadrant, and we need the negative sign).
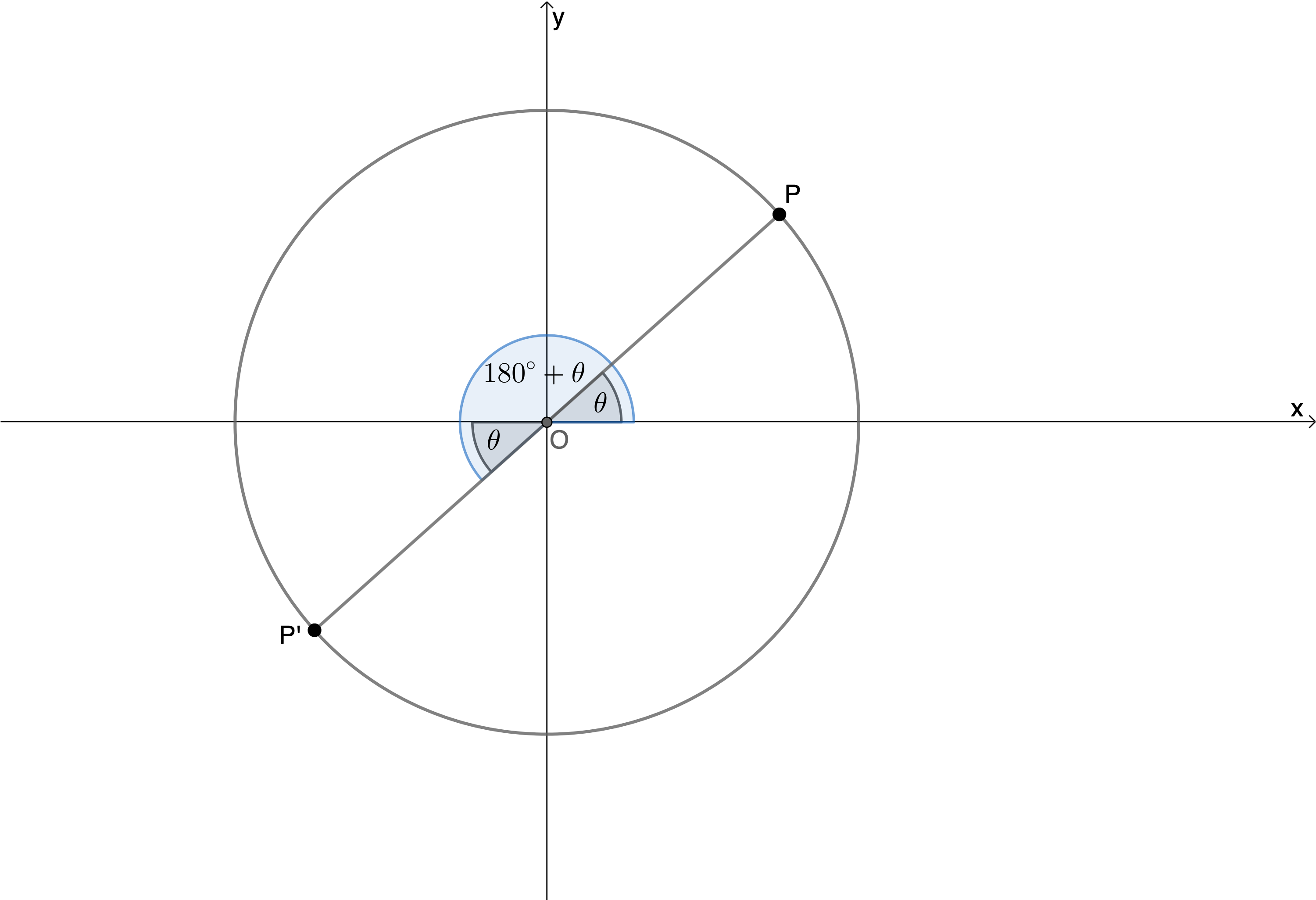
The same is true for angles in the third and fourth quadrants where:
- [latex]\scriptsize \sin ({{270}^\circ}-\theta )=-\cos \theta[/latex] and [latex]\scriptsize \cos ({{270}^\circ}-\theta )=-\sin \theta[/latex] (sine and cosine are both negative in the third quadrant)
- [latex]\scriptsize \sin ({{270}^\circ}+\theta )=-\cos \theta[/latex] and [latex]\scriptsize \cos ({{270}^\circ}+\theta )=\sin \theta[/latex] (only sine is negative in the fourth quadrant).
Note: The co-function reduction rules for [latex]\scriptsize {{270}^\circ}\pm \theta[/latex] are not officially part of the NC(V) level 3 curriculum.
Co-function reduction rules:
- [latex]\scriptsize \sin ({{90}^\circ}-\theta )=\cos \theta[/latex]
- [latex]\scriptsize \sin ({{90}^\circ}+\theta )=\cos \theta[/latex]
- [latex]\scriptsize \cos ({{90}^\circ}-\theta )=\sin \theta[/latex]
- [latex]\scriptsize \cos ({{90}^\circ}+\theta )=-\sin \theta[/latex] ̶ cosine is negative in the second quadrant hence the need for the negative sign
Example 2.4
Write the following as ratios of [latex]\scriptsize {{20}^\circ}[/latex]:
- [latex]\scriptsize \sin {{70}^\circ}[/latex]
- [latex]\scriptsize \cos {{110}^\circ}[/latex]
- [latex]\scriptsize \sin {{250}^\circ}[/latex]
- [latex]\scriptsize \cos (\theta -{{90}^\circ})[/latex]
Solutions
- [latex]\scriptsize \begin{align*}\sin {{70}^\circ}&=\sin ({{90}^\circ}-{{20}^\circ})\\&=\cos {{20}^\circ}\end{align*}[/latex]
- .
[latex]\scriptsize \begin{align*}\cos {{110}^\circ}&=\cos ({{90}^\circ}+{{20}^\circ})\\&=-\sin {{20}^\circ}\quad \text{Don }\!\!'\!\!\text{ t forget the negative sign; cosine is negative in the second quadrant}\end{align*}[/latex] - We could answer this as follows:
[latex]\scriptsize \sin {{250}^\circ}=\sin ({{270}^\circ}-{{20}^\circ})=-\cos {{20}^\circ}[/latex]However, the [latex]\scriptsize {{270}^\circ}\pm \theta[/latex] co-function reduction rules are not part of the curriculum, so we answer it as follows:
[latex]\scriptsize \begin{align*}\sin {{250}^\circ}&=\sin ({{180}^\circ}+{{70}^\circ})\\&=-\sin {{70}^\circ}\\&=-\sin ({{90}^\circ}-{{20}^\circ})\\&=-\cos {{20}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\cos (\theta -{{90}^\circ})&=\cos (-{{90}^\circ}+\theta )\\&=\cos \left( {-({{{90}}^\circ}-\theta )} \right)&& \text{The angle }-({{90}^\circ}-\theta )\text{ is in the fourth quadrant where}\\ &&&\text{cosine is positive}\\&=\cos ({{90}^\circ}-\theta )\\&=\sin \theta \end{align*}[/latex]
Example 2.5
Express the following with all ratios in terms of [latex]\scriptsize \theta[/latex] alone and simplify:
[latex]\scriptsize \displaystyle \frac{{\text{cos(}\theta -\text{9}{{\text{0}}^\circ}\text{) cos(72}{{\text{0}}^\circ}+\theta \text{) tan(}\theta -\text{36}{{\text{0}}^\circ})}}{{\text{si}{{\text{n}}^{2}}\text{(}\theta \text{+36}{{\text{0}}^\circ}\text{) cos(}\theta \text{+9}{{\text{0}}^\circ}\text{)}}}[/latex]
Solution
Let’s break this question down and look at each trig ratio separately first.
- .
[latex]\scriptsize \begin{align*}\cos (\theta -{{90}^\circ})&=\cos (-{{90}^\circ}+\theta )\\&=\cos \left( {-({{{90}}^\circ}-\theta )} \right)\quad -({{90}^\circ}-\theta )\text{ is in the fourth quadrant where cosine is positive}\\&=\cos ({{90}^\circ}-\theta )\\&=\sin \theta \end{align*}[/latex]- [latex]\scriptsize \cos ({{720}^\circ}+\theta )=\cos \theta\quad \text{because }{{720}^\circ}\text{ is just two full revolutions or two full periods}[/latex]
- [latex]\scriptsize \tan (\theta -{{360}^\circ})=\tan \theta \quad -{{360}^\circ}\text{ is one full revolution or two full periods}[/latex]
- [latex]\scriptsize {{\sin }^{2}}(\theta +{{360}^\circ})={{\sin }^{2}}\theta \quad {{360}^\circ}\text{ is one full revolution or one full period}[/latex]
- [latex]\scriptsize \cos (\theta +{{90}^\circ})=\cos ({{90}^\circ}+\theta )=-\sin \theta[/latex]
Therefore:
[latex]\scriptsize \begin{align*}\displaystyle \frac{\cos(\theta-90^\circ)\cos(720^\circ+\theta)\tan(\theta-360^\circ)}{\sin^2(\theta+360^\circ)\cos(\theta+90^\circ)}=\displaystyle\frac{\sin\theta\cos\theta\tan\theta}{\sin^2\theta(-\sin\theta)}\end{align*}[/latex]Now we can simplify the expression.
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin \theta \text{ cos}\theta \text{ tan}\theta }}{{\text{si}{{\text{n}}^{2}}\theta (-\text{sin}\theta )}}&=\displaystyle \frac{{\bcancel{{\sin \theta }}\text{ cos}\theta \text{ tan}\theta }}{{\text{si}{{\text{n}}^{2}}\theta (-\bcancel{{\text{sin}\theta }})}}\\&=-\displaystyle \frac{{\cos \theta \tan \theta }}{{{{{\sin }}^{2}}\theta }}\end{align*}[/latex]
Exercise 2.2
- Simplify the following to a ratio of [latex]\scriptsize {{38}^\circ}[/latex]:
- [latex]\scriptsize \sin {{52}^\circ}[/latex]
- [latex]\scriptsize \sin {{128}^\circ}[/latex]
- [latex]\scriptsize \cos {{128}^\circ}[/latex]
- [latex]\scriptsize \sin {{308}^\circ}[/latex]
- Simplify the following expressions:
- [latex]\scriptsize \displaystyle \frac{{\cos ({{{90}}^\circ}+\theta )\sin ({{{90}}^\circ}+\theta )}}{{\sin ({{{90}}^\circ}-\theta )\sin ({{{180}}^\circ}+\theta )}}[/latex]
- [latex]\scriptsize \displaystyle \frac{{2\sin ({{{90}}^\circ}-x)\sin ({{{90}}^\circ}+x)}}{{{{{\cos }}^{2}}({{{90}}^\circ}+x)+\cos ({{{180}}^\circ}+x)}}[/latex]
- Determine the value of the following expression without a calculator:
[latex]\scriptsize \displaystyle \frac{{\tan {{{225}}^\circ}-{{{\sin }}^{2}}{{{300}}^\circ}}}{{\cos ({{{90}}^\circ}+{{{30}}^\circ})}}[/latex]
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- The reduction rules for sine, cosine and tangent:
- [latex]\scriptsize \sin ({{180}^\circ}-\theta )=\sin \theta[/latex]
- [latex]\scriptsize \sin ({{180}^\circ}+\theta )=-\sin \theta[/latex]
- [latex]\scriptsize \sin ({{360}^\circ}-\theta )=\sin \theta[/latex] or [latex]\scriptsize \sin (-\theta )=\sin \theta[/latex]
- [latex]\scriptsize \cos ({{180}^\circ}-\theta )=-\cos \theta[/latex]
- [latex]\scriptsize \cos ({{180}^\circ}+\theta )=-\cos \theta[/latex]
- [latex]\scriptsize \cos ({{360}^\circ}-\theta )=\cos \theta[/latex] or [latex]\scriptsize \cos (-\theta )=\cos \theta[/latex]
- [latex]\scriptsize \tan ({{180}^\circ}-\theta )=-\tan \theta[/latex]
- [latex]\scriptsize \tan ({{180}^\circ}+\theta )=\tan \theta[/latex]
- [latex]\scriptsize \tan ({{360}^\circ}-\theta )=-\tan \theta[/latex] or [latex]\scriptsize \tan (-\theta )=-\tan \theta[/latex].
- The co-function reduction rules for sine and cosine for [latex]\scriptsize {{90}^\circ}\pm \theta[/latex]:
- [latex]\scriptsize \sin ({{90}^\circ}-\theta )=\cos \theta[/latex]
- [latex]\scriptsize \sin ({{90}^\circ}+\theta )=\cos \theta[/latex]
- [latex]\scriptsize \cos ({{90}^\circ}-\theta )=\sin \theta[/latex]
- [latex]\scriptsize \cos ({{90}^\circ}+\theta )=-\sin \theta[/latex].
Unit 2: Assessment
Suggested time to complete: 25 minutes
- Write the following as a function of an angle less than [latex]\scriptsize {{45}^\circ}[/latex]:
- [latex]\scriptsize \sin {{167}^\circ}[/latex]
- [latex]\scriptsize \tan {{214}^\circ}[/latex]
- [latex]\scriptsize \cos (-{{236}^\circ})[/latex]
- If [latex]\scriptsize {{\cos }^{2}}\theta =\displaystyle \frac{{16}}{{25}}[/latex] and [latex]\scriptsize {{0}^\circ}\le \theta \le {{90}^\circ}[/latex], calculate the following:
- [latex]\scriptsize \cos \theta[/latex]
- [latex]\scriptsize \tan ({{180}^\circ}-\theta )[/latex]
- [latex]\scriptsize {{\cos }^{2}}({{180}^\circ}+\theta )+{{\sin }^{2}}({{180}^\circ}+\theta )[/latex]
- [latex]\scriptsize \displaystyle \frac{{\sin (-\theta )\cos ({{{180}}^\circ}+\theta )\cos ({{{90}}^\circ}+\theta )}}{{\tan ({{{360}}^\circ}-\theta )\sin ({{{90}}^\circ}+\theta )}}[/latex]
- Prove that [latex]\scriptsize \displaystyle \frac{{\sin {{{210}}^\circ}\cos {{{150}}^\circ}\tan {{{315}}^\circ}}}{{\sin {{{120}}^\circ}}}=\displaystyle \frac{1}{2}[/latex].
- Determine the value of the following without a calculator:
- [latex]\scriptsize \displaystyle \frac{{\cos (-{{{30}}^\circ})}}{{\tan {{{150}}^\circ}}}+\sin {{330}^\circ}[/latex]
- [latex]\scriptsize \sin {{780}^\circ}-(\cos {{315}^\circ})(\sin {{405}^\circ})[/latex]
- [latex]\scriptsize \sqrt{2}\tan {{150}^\circ}.\cos {{225}^\circ}.\sin {{240}^\circ}[/latex]
The full solutions are at the end of the unit.
Unit 2: Solutions
Exercise 2.1
- .
- .
[latex]\scriptsize \begin{align*}\cos {{257}^\circ}&=\cos ({{180}^\circ}+{{77}^\circ})\\&=-\cos {{77}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\tan {{198}^\circ}&=\tan ({{180}^\circ}+{{18}^\circ})\\&=\tan {{18}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\tan {{162}^\circ}&=\tan ({{180}^\circ}-{{18}^\circ})\\&=-\tan {{18}^\circ}\end{align*}[/latex] - [latex]\scriptsize \tan (-{{18}^\circ})=-\tan {{18}^\circ}[/latex]
- .
[latex]\scriptsize \begin{align*}\sin {{241}^\circ}&=\sin ({{180}^\circ}+{{61}^\circ})\\&=-\sin {{61}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin {{{67}}^\circ}}}{{\tan {{{293}}^\circ}}}+\cos {{113}^\circ}&=\displaystyle \frac{{\sin {{{67}}^\circ}}}{{\tan ({{{360}}^\circ}-{{{67}}^\circ})}}+\cos ({{180}^\circ}-{{67}^\circ})\\&=\displaystyle \frac{{\sin {{{67}}^\circ}}}{{-\tan {{{67}}^\circ}}}-\cos {{67}^\circ}\end{align*}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{{{{\tan }}^{2}}{{{225}}^\circ}-\sin (-{{{30}}^\circ})\cos (-{{{30}}^\circ})}}{{\tan {{{300}}^\circ}}}&=\displaystyle \frac{{{{{\tan }}^{2}}({{{180}}^\circ}+{{{45}}^\circ})+\sin {{{30}}^\circ}\cos {{{30}}^\circ}}}{{\tan ({{{360}}^\circ}-{{{60}}^\circ})}}\\&=\displaystyle \frac{{{{{\tan }}^{2}}{{{45}}^\circ}+\sin {{{30}}^\circ}\cos {{{30}}^\circ}}}{{-\tan {{{60}}^\circ}}}\\&=\displaystyle \frac{{{{1}^{2}}+\displaystyle \frac{1}{2}\times \displaystyle \frac{{\sqrt{3}}}{2}}}{{-\displaystyle \frac{{\sqrt{3}}}{1}}}\\&=\displaystyle \frac{{1+\displaystyle \frac{{\sqrt{3}}}{4}}}{{-\sqrt{3}}}\\&=\displaystyle \frac{{\displaystyle \frac{{4+\sqrt{3}}}{4}}}{{-\sqrt{3}}}\\&=\displaystyle \frac{{4+\sqrt{3}}}{4}\times \displaystyle \frac{1}{{-\sqrt{3}}}\\&=\displaystyle \frac{{4+\sqrt{3}}}{{-4\sqrt{3}}}\quad \text{Multiply by }\displaystyle \frac{{\sqrt{3}}}{{\sqrt{3}}}\\&=-\displaystyle \frac{{4\sqrt{3}+3}}{{12}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{\left( {\displaystyle \frac{{\sin {{{210}}^\circ}}}{{\cos {{{210}}^\circ}}}} \right)}^{2}}+2\tan {{210}^\circ}&={{\left( {\displaystyle \frac{{\sin ({{{180}}^\circ}+{{{30}}^\circ})}}{{\cos ({{{180}}^\circ}+{{{30}}^\circ})}}} \right)}^{2}}+2\tan ({{180}^\circ}+{{30}^\circ})\\&={{\left( {\displaystyle \frac{{-\displaystyle \frac{1}{2}}}{{-\displaystyle \frac{{\sqrt{3}}}{2}}}} \right)}^{2}}+2\times \displaystyle \frac{1}{{\sqrt{3}}}\\&={{\left( {\displaystyle \frac{1}{2}\times \displaystyle \frac{2}{{\sqrt{3}}}} \right)}^{2}}+\displaystyle \frac{2}{{\sqrt{3}}}\\&={{\left( {\displaystyle \frac{2}{{2\sqrt{3}}}} \right)}^{2}}+\displaystyle \frac{2}{{\sqrt{3}}}\\&=\displaystyle \frac{4}{{12}}+\displaystyle \frac{2}{{\sqrt{3}}}\\&=\displaystyle \frac{{\sqrt{3}+6}}{{3\sqrt{3}}}\\&=\displaystyle \frac{{3+6\sqrt{3}}}{9}\\&=\displaystyle \frac{{3\left( {1+2\sqrt{3}} \right)}}{9}\\&=\displaystyle \frac{{1+2\sqrt{3}}}{3}\end{align*}[/latex]
- .
Exercise 2.2
- .
- [latex]\scriptsize \sin {{52}^\circ}=\sin ({{90}^\circ}-{{38}^\circ})=\cos {{38}^\circ}[/latex]
- [latex]\scriptsize \sin {{128}^\circ}=\sin ({{90}^\circ}+{{38}^\circ})=\cos {{38}^\circ}[/latex]
- [latex]\scriptsize \cos {{128}^\circ}=\cos ({{90}^\circ}+{{38}^\circ})=-\sin {{38}^\circ}[/latex]
- [latex]\scriptsize \sin {{308}^\circ}=\sin ({{360}^\circ}-{{52}^\circ})=-\sin {{52}^\circ}=-\sin ({{90}^\circ}-{{38}^\circ})=-\cos {{38}^\circ}[/latex]
- .
- .
[latex]\scriptsize \begin{align*} \displaystyle \frac{\cos(90^\circ+\theta)\sin(90^\circ+\theta)}{\sin(90^\circ-\theta)\sin(180^\circ+\theta)} &=\displaystyle \frac{-\sin\theta\cos\theta}{\cos\theta(-\sin\theta)}\\ &=1 \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*} &\displaystyle \frac{2\sin(90^\circ-x)\sin(90^\circ+x)}{\cos^2(90^\circ+x)+\cos(180^\circ+x)}&&\left[ \cos^2(90^\circ +x)=\cos(90^\circ +x)\cos(90^\circ +x)=(-\sin x)(-\sin x)=\sin^2 x\right]\\ &=\displaystyle \frac{2\cos x\cos x}{\sin^2 x-\cos x}\\ &=\displaystyle \frac{2\cos^2 x}{\sin^2 x-\cos x} \end{align*}[/latex]
- .
- .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\tan {{{225}}^\circ}-{{{\sin }}^{2}}{{{300}}^\circ}}}{{\cos ({{{90}}^\circ}+{{{30}}^\circ})}}&=\displaystyle \frac{{\tan \left( {{{{180}}^\circ}+{{{45}}^\circ}} \right)-{{{\sin }}^{2}}({{{360}}^\circ}-{{{60}}^\circ})}}{{-\sin {{{30}}^\circ}}}\\&=\displaystyle \frac{{\tan {{{45}}^\circ}-{{{\sin }}^{2}}{{{60}}^\circ}}}{{-\sin {{{30}}^\circ}}}\quad \left[ {{{{\sin }}^{2}}({{{360}}^\circ}-{{{60}}^\circ})=\sin ({{{360}}^\circ}-{{{60}}^\circ})\times \sin ({{{360}}^\circ}-{{{60}}^\circ})} \right]\\&=\displaystyle \frac{{1-{{{\left( {\displaystyle \frac{{\sqrt{3}}}{2}} \right)}}^{2}}}}{{-\displaystyle \frac{1}{2}}}\\&=\displaystyle \frac{{1-\displaystyle \frac{3}{4}}}{{-\displaystyle \frac{1}{2}}}\\&=\displaystyle \frac{{\displaystyle \frac{1}{4}}}{{-\displaystyle \frac{1}{2}}}\\&=-\displaystyle \frac{1}{4}\times \displaystyle \frac{2}{1}\\&=-\displaystyle \frac{1}{2}\end{align*}[/latex]
Unit 2: Assessment
- .
- [latex]\scriptsize \sin {{167}^\circ}=\sin ({{180}^\circ}-{{13}^\circ})=\sin {{13}^\circ}[/latex]
- [latex]\scriptsize \tan {{214}^\circ}=\tan ({{180}^\circ}+{{34}^\circ})=\tan {{34}^\circ}[/latex]
- [latex]\scriptsize \cos (-{{236}^\circ})=\cos (-{{236}^\circ}+{{360}^\circ})=\cos {{124}^\circ}=\cos ({{90}^\circ}+{{34}^\circ})=-\sin {{34}^\circ}[/latex]
- [latex]\scriptsize \cos^2 \theta=\displaystyle \frac{16}{25}[/latex] and [latex]\scriptsize 0^\circ\le\theta\le90^\circ[/latex]
To complete the question, we need to find the missing side of the triangle.
[latex]\scriptsize \begin{align*}{{y}^{2}}+{{4}^{2}} & ={{5}^{2}}\\\therefore {{y}^{2}} & =25-16=9\\\therefore y & =3\end{align*}[/latex]- [latex]\scriptsize \cos \theta =\displaystyle \frac{4}{5}[/latex]
- [latex]\scriptsize \tan ({{180}^\circ}-\theta )=-\tan \theta =-\displaystyle \frac{3}{4}[/latex]
- .
[latex]\scriptsize \begin{align*}\cos^2(180^\circ+\theta)+\sin^2(180^\circ+\theta) &=\cos^2\theta+\sin^2\theta\\ &=\displaystyle \frac{16}{25}+\displaystyle \frac{9}{25}\\ &=1 \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*} \displaystyle \frac{-\sin\theta\cos(180^\circ+\theta)\cos(90^\circ+\theta)}{\tan(360^\circ-\theta)\sin(90^\circ+\theta)} &=\displaystyle \frac{-\sin\theta(-\cos\theta)(-\sin\theta)}{(-\tan\theta)\cos\theta}\\ &=\displaystyle \frac{\sin^2\theta\cos\theta}{\tan\theta\cos\theta}\\ &=\displaystyle \frac{\displaystyle \frac{9}{25}}{\displaystyle \frac{3}{4}}\\ &=\displaystyle \frac{9}{25}\times \displaystyle \frac{4}{3}\\ &=\displaystyle \frac{12}{25} \end{align*}[/latex]
- .
[latex]\scriptsize \begin{align*} \text{LHS}&=\displaystyle \frac{\sin210^\circ\cos150^\circ\tan315^\circ}{\sin120^\circ}\\ &=\displaystyle \frac{\sin(180^\circ+30^\circ)\cos(180^\circ-30^\circ)\tan(360^\circ-45^\circ)}{\sin(180^\circ-60^\circ)}\\ &=\displaystyle \frac{(-\sin30^\circ)(-\cos30^\circ)(-\tan45^\circ)}{\sin60^\circ}\\ &=\displaystyle \frac{-\displaystyle \frac{1}{2}\cdot-\displaystyle \frac{\sqrt{3}}{2}\cdot-1}{\displaystyle \frac{\sqrt{3}}{2}}\\ &=\displaystyle \frac{-\displaystyle \frac{\sqrt{3}}{4}}{\displaystyle \frac{\sqrt{3}}{2}}\\ &=-\displaystyle \frac{\sqrt{3}}{4}\times\displaystyle \frac{2}{\sqrt{3}}\\ &=-\displaystyle \frac{1}{2}=\text{RHS} \end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\cos (-{{{30}}^\circ})}}{{\tan {{{150}}^\circ}}}+\sin {{330}^\circ}&=\displaystyle \frac{{\cos {{{30}}^\circ}}}{{\tan ({{{180}}^\circ}-{{{30}}^\circ})}}+\sin ({{360}^\circ}-{{30}^\circ})\\&=\displaystyle \frac{{\cos {{{30}}^\circ}}}{{-\tan {{{30}}^\circ}}}-\sin {{30}^\circ}\\&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{3}}}{2}}}{{-\displaystyle \frac{1}{{\sqrt{3}}}}}-\displaystyle \frac{1}{2}\\&=\displaystyle \frac{{\sqrt{3}}}{2}\times \left( {-\displaystyle \frac{{\sqrt{3}}}{1}} \right)-\displaystyle \frac{1}{2}\\&=-\displaystyle \frac{3}{2}-\displaystyle \frac{1}{2}\\&=-2\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\sin {{780}^\circ}-(\cos {{315}^\circ})(\sin {{405}^\circ})&=\sin ({{720}^\circ}+{{60}^\circ})-\left( {\cos ({{{360}}^\circ}-{{{45}}^\circ})} \right)\left( {\sin ({{{360}}^\circ}+{{{45}}^\circ}} \right)\\&=\sin (2\times {{360}^\circ}+{{60}^\circ})-\left( {\cos ({{{360}}^\circ}-{{{45}}^\circ})} \right)\left( {\sin ({{{360}}^\circ}+{{{45}}^\circ}} \right)\\&=\sin {{60}^\circ}-\cos {{45}^\circ}\sin {{45}^\circ}\\&=\displaystyle \frac{{\sqrt{3}}}{2}-\displaystyle \frac{1}{{\sqrt{2}}}\times \displaystyle \frac{1}{{\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{3}}}{2}-\displaystyle \frac{1}{2}\\&=\displaystyle \frac{{\sqrt{3}-1}}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\sqrt{2}\tan {{150}^\circ}.\cos {{225}^\circ}.\sin {{240}^\circ}&=\sqrt{2}\tan ({{180}^\circ}-{{30}^\circ}).\cos ({{180}^\circ}+{{45}^\circ}).\sin ({{180}^\circ}+{{60}^\circ})\\&=\sqrt{2}(-\tan {{30}^\circ}).(-\cos {{45}^\circ}).(-\sin {{60}^\circ})\\&=\sqrt{2}\left( {-\displaystyle \frac{1}{{\sqrt{3}}}} \right)\cdot \left( {-\displaystyle \frac{1}{{\sqrt{2}}}} \right)\cdot \left( {-\displaystyle \frac{{\sqrt{3}}}{2}} \right)\\&=-\displaystyle \frac{{\sqrt{6}}}{{2\sqrt{6}}}\\&=-\displaystyle \frac{1}{2}\end{align*}[/latex]
- .
Media Attributions
- figure1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure3 © DHET is licensed under a CC BY (Attribution) license
- figure4 © DHET is licensed under a CC BY (Attribution) license
- figure5 © DHET is licensed under a CC BY (Attribution) license
- figure6 © DHET is licensed under a CC BY (Attribution) license
- 180-theta © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- 180+theta © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- 360-theta © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure7 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure8 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure9 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
