Unit outcomes

By the end of this unit you will be able to:

• Apply the area rule in 2-D triangles.

What you should know

Before you start this unit, make sure you can:

• Calculate the area of a triangle using the formula [latex]\scriptsize \text{area}=\displaystyle \frac{1}{2}\times b\times h[/latex].
• Use a calculator to calculate the sine of a given angle. Refer to level 2 subject outcome 3.6 unit 2 if you need help with this.
• Use a calculator to calculate the angle from a given ratio for sine. Refer to level 2 subject outcome 3.6 unit 2 if you need help with this.

Introduction

Trigonometry is not just useful for finding the lengths of unknown sides or the sizes of unknown angles in right-angled triangles. It can also be put to work in non-right-angled triangles and it can be used to find measures other than the lengths of sides and the sizes of angles.

The area rule, for example, is a useful trigonometric identity (remember those from unit 3?) that can be used to find the area of any triangle, even triangles that have no [latex]\scriptsize {{90}^\circ}[/latex] angles. But why do we need another way to calculate the area of a triangle if we already have the well-known formula [latex]\scriptsize \text{Area}=\displaystyle \frac{1}{2}\times b\times h[/latex]? Well, sometimes, we might not know the length of the perpendicular height or the base. Instead, we might know the size of one of the angles inside the triangle.

In this unit, we are going to derive the area rule and see how to use it to find the areas of all sorts of different triangles in different contexts.

Derive the area rule

Deriving the area rule is not too difficult. You will be led through this process in Activity 5.1.

Activity 5.1: Derive the area rule

Time required: 15 minutes

What you need:

• a piece of paper
• a pen or pencil
• a ruler

What to do:

1. On your piece of paper, draw any triangle [latex]\scriptsize \text{ABC}[/latex] and label the sides in relation to the opposite vertices (see Figure 1). The triangle can be any size and shape.
2. Now drop a perpendicular from [latex]\scriptsize \text{B}[/latex] to the opposite side and call this perpendicular [latex]\scriptsize h[/latex] (see Figure 2).
3. Write the expression for the area of triangle [latex]\scriptsize \text{ABC}[/latex] based on its base and perpendicular height.
4. Write an expression for [latex]\scriptsize \sin \text{A}[/latex].
5. Write a new expression for the area of triangle [latex]\scriptsize \text{ABC}[/latex] that includes the term [latex]\scriptsize \sin A[/latex]. Hint: look for a substitution.
6. Now, write an expression for [latex]\scriptsize \sin \text{C}[/latex] and then write a similar expression for the area of the triangle in terms of[latex]\scriptsize \sin \text{C}[/latex].
7. What do you think the area of triangle [latex]\scriptsize \text{ABC}[/latex] would be in terms of [latex]\scriptsize \sin \text{B}[/latex]?

What did you find?

1. Remember that your triangle [latex]\scriptsize \text{ABC}[/latex] can be any size and shape. Figure 1 shows just one possible triangle.
   

   

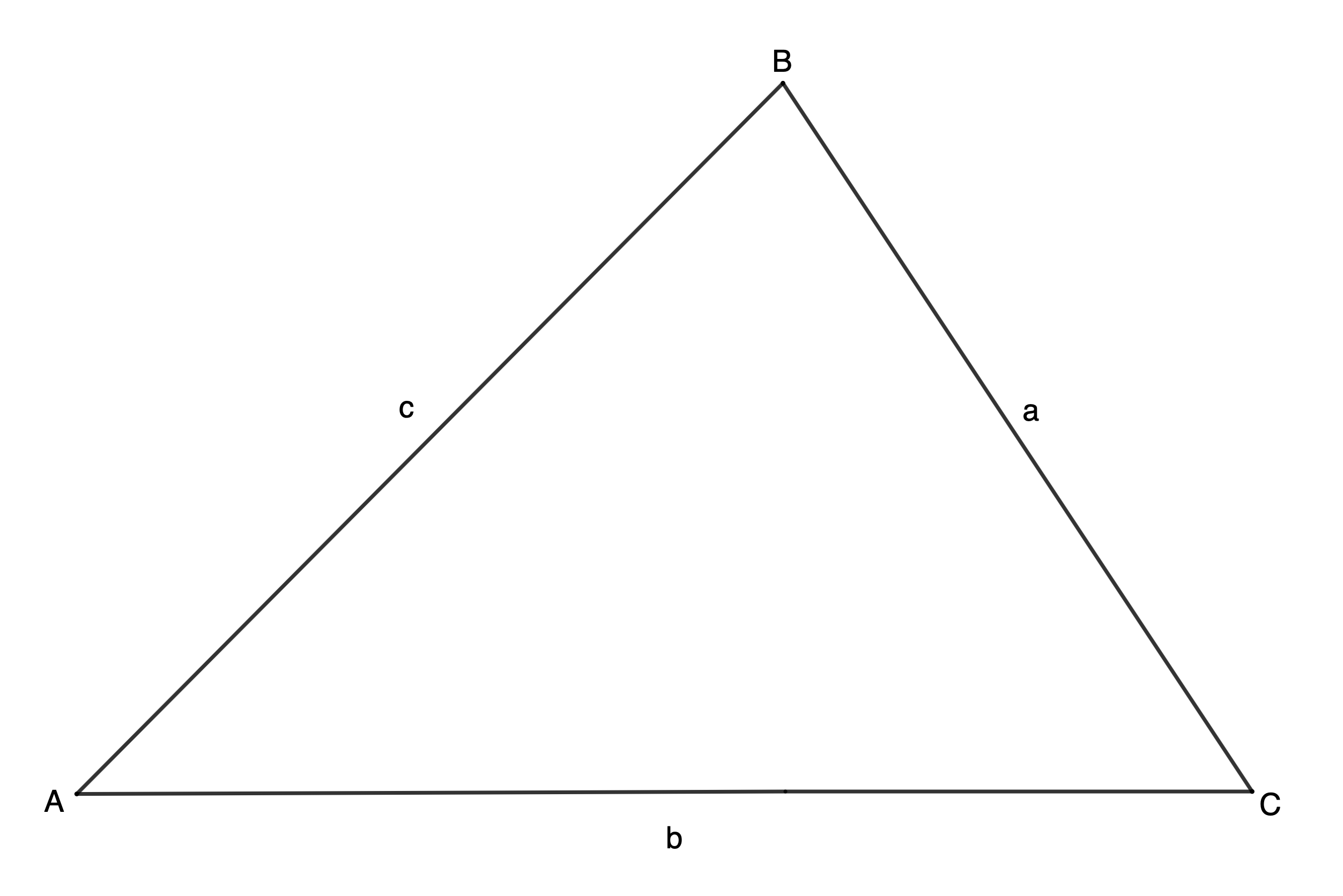
2. Remember that dropping a perpendicular means that the new line meets the other line at [latex]\scriptsize {{90}^\circ}[/latex]. Figure 2 shows what your perpendicular line may look like.
   

   

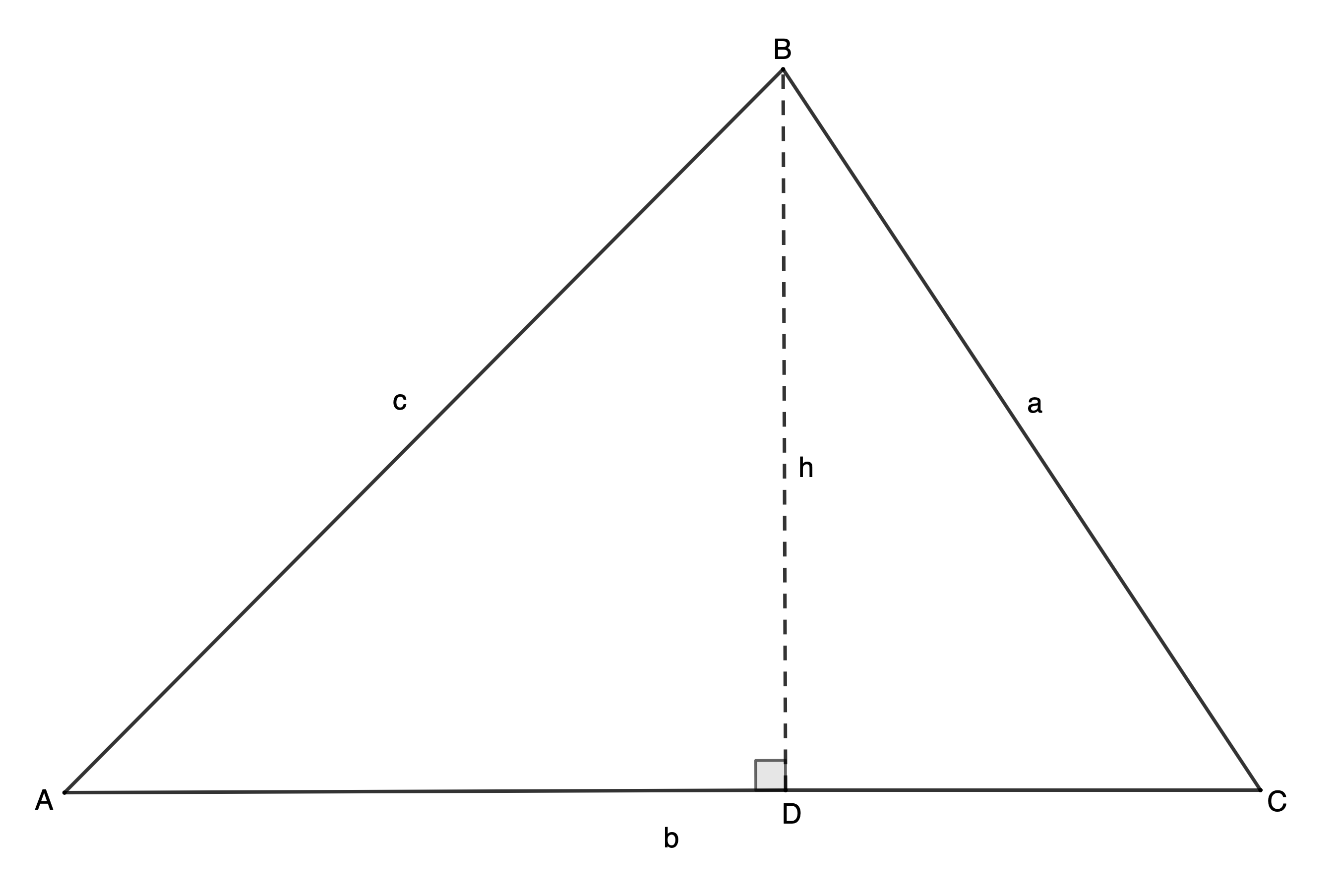
3. The area of triangle [latex]\scriptsize \text{ABC}[/latex] is given by [latex]\scriptsize A=\displaystyle \frac{1}{2}\times b\times h[/latex] where the base is side [latex]\scriptsize \text{b}[/latex] and the perpendicular height is [latex]\scriptsize \text{h}[/latex]. Therefore, area of [latex]\scriptsize \Delta \text{ABC}[/latex] is [latex]\scriptsize \displaystyle \frac{1}{2}\times \text{b}\times \text{h}[/latex].
4. [latex]\scriptsize \sin \text{A}=\displaystyle \frac{{\text{opposite}}}{{\text{hypotenuse}}}=\displaystyle \frac{\text{h}}{\text{c}}[/latex].
5. [latex]\scriptsize \sin \text{A}=\displaystyle \frac{\text{h}}{\text{c}}\therefore \text{h}=\text{c}\times \sin \text{A}[/latex]. But area [latex]\scriptsize \Delta \text{ABC}[/latex] is [latex]\scriptsize \displaystyle \frac{1}{2}\times \text{b}\times \text{h}[/latex]. Therefore, area [latex]\scriptsize \Delta \text{ABC}=\displaystyle \frac{1}{2}\times \text{b}\times \text{c}\times \sin text{A}=\displaystyle \frac{1}{2}\text{bc}\sin \text{A}[/latex].
6. [latex]\scriptsize \sin \text{C}=\displaystyle \frac{{\text{opposite}}}{{\text{hypotenuse}}}=\displaystyle \frac{\text{h}}{\text{a}}[/latex]. Therefore [latex]\scriptsize \text{h}=\text{a}\times \sin \text{C}[/latex] and area [latex]\scriptsize \Delta \text{ABC}=\displaystyle \frac{1}{2}\times \text{b}\times \text{a}\times \sin\text{C}=\displaystyle \frac{1}{2}\text{ab}\sin \text{C}[/latex]
7. In each case above, the expression for the area of the triangle is the product of the length of two sides and the sine of the angle between these two sides. Therefore, area [latex]\scriptsize \Delta \text{ABC}=\displaystyle \frac{1}{2}\text{ac}\sin \text{B}[/latex].

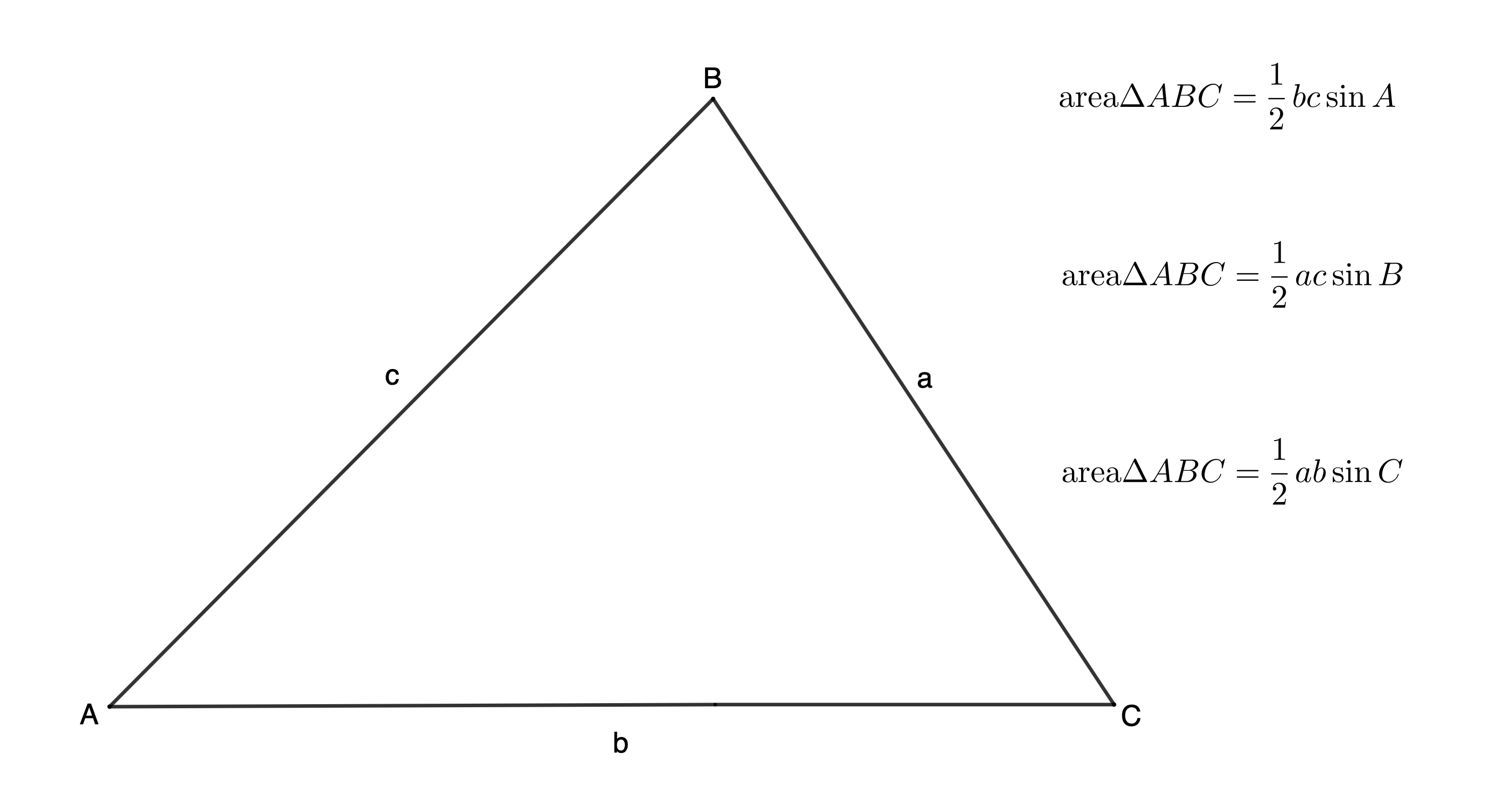
Take note!

The area rule works for any triangle for which you know the length of any two sides and the size of the included angle (the angle between the two known sides).

Use the area rule

Let’s look at some examples of how to apply the area rule.

Example 5.2

Find the area of [latex]\scriptsize \Delta \text{ABC}[/latex] correct to two decimal places.

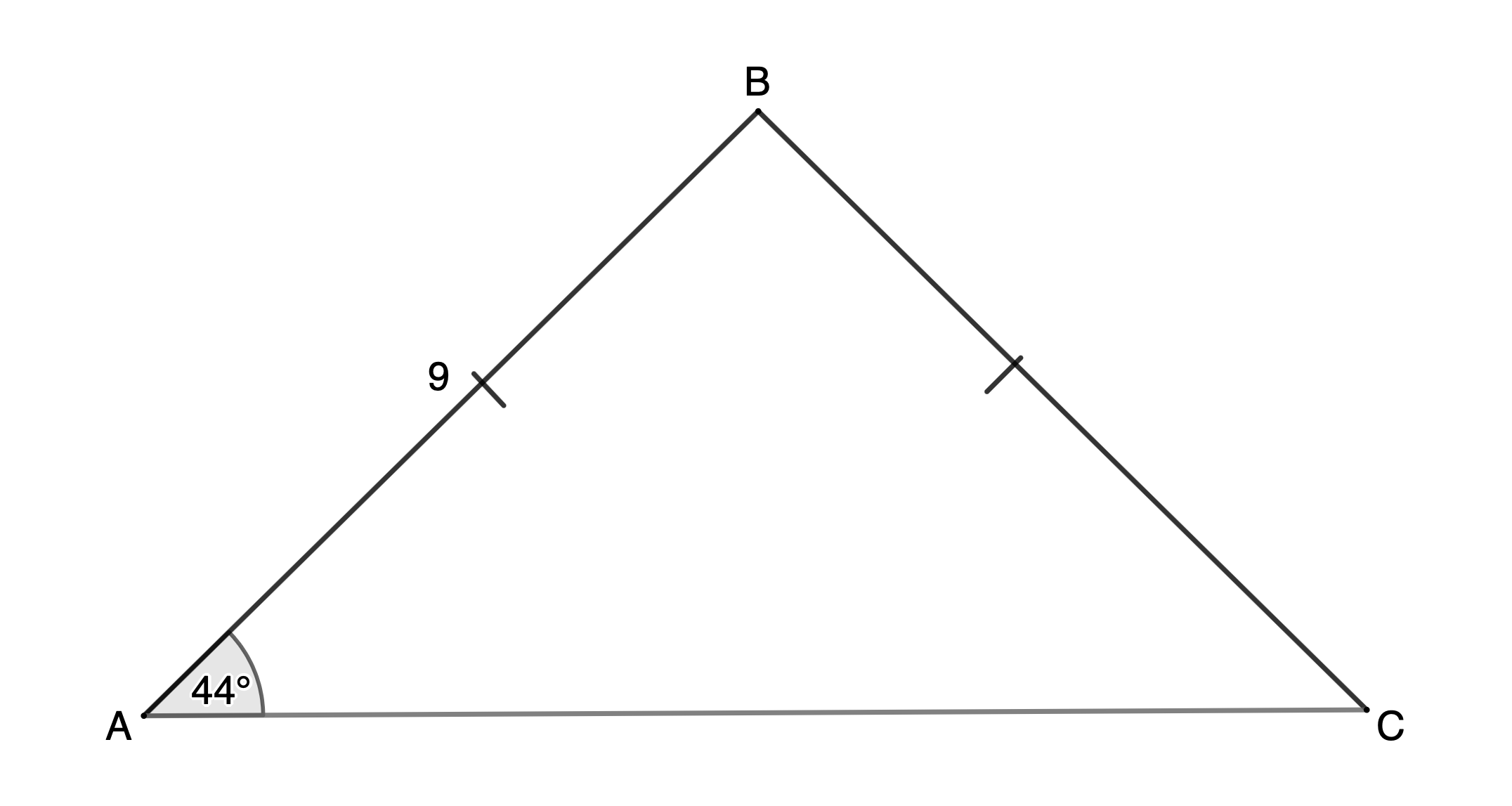
Solution

We are not given the lengths of two sides and the included angle, so we cannot use the area rule with the information we currently have. We need to find the size of [latex]\scriptsize \hat{B}[/latex]. To do this, we can use the fact that [latex]\scriptsize AB=BC[/latex] (given) and therefore, [latex]\scriptsize \hat{A}=\hat{C}={{43}^\circ}[/latex] (angles opposite equal sides). Then we can use that fact that angles in a triangle are supplementary to find [latex]\scriptsize \hat{B}[/latex].

[latex]\scriptsize AB=BC[/latex] (given)
[latex]\scriptsize \therefore \hat{A}=\hat{C}={{43}^\circ}[/latex] (angles opposite equal sides)
[latex]\scriptsize \begin{align*}\therefore \hat{B} & ={{180}^\circ}-\hat{A}-\hat{C}\\ & ={{180}^\circ}-{{43}^\circ}-{{43}^\circ}\\ & ={{94}^\circ}\end{align*}[/latex] (angles in a triangle are supplementary)

Now we can use the area rule.
[latex]\scriptsize \begin{align*}\text{Area }\Delta ABC&=\displaystyle \frac{1}{2}ac\sin B\\&=\displaystyle \frac{1}{2}\times 8\times 8\times \sin {{94}^\circ}\\&=31.92\ {{\text{m}}^{2}}\end{align*}[/latex]

Remember to round off your final answer and include the correct area units.

Example 5.3

A parallelogram has adjacent sides of [latex]\scriptsize 16\ \text{cm}[/latex] and [latex]\scriptsize 23\ \text{cm}[/latex]. The angle between them is [latex]\scriptsize {{43}^\circ}[/latex]. Calculate the area of the parallelogram correct to two decimal places.

Solution

If no diagram is given, it is always best to draw your own using the given information. This does not have to be accurate.

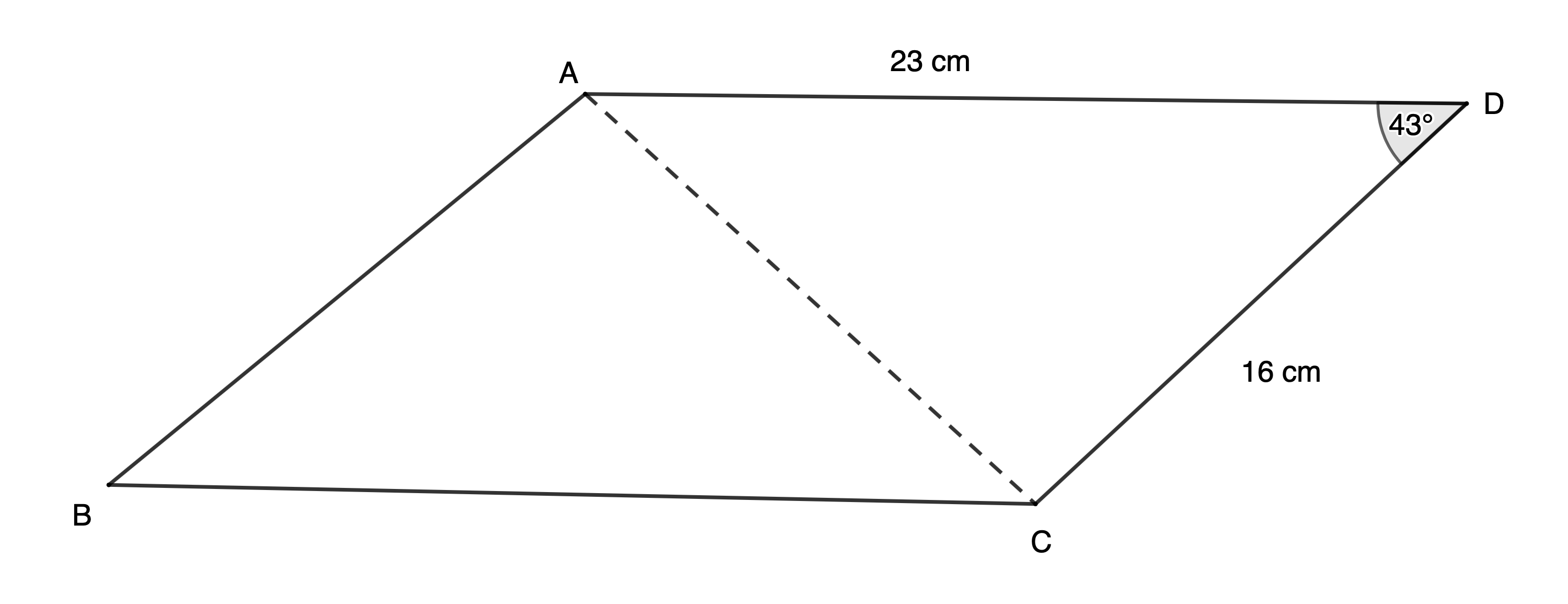
We know that [latex]\scriptsize ABCD[/latex] is a parallelogram. Therefore, if we can find the area of [latex]\scriptsize \Delta ACD[/latex] we can multiply this by [latex]\scriptsize 2[/latex] to find the area of [latex]\scriptsize ABCD[/latex].

In [latex]\scriptsize \Delta ACD[/latex], we know two sides and the included angle so we can use the area rule.
[latex]\scriptsize \begin{align*}\text{Area }\Delta ADC&=\displaystyle \frac{1}{2}ac\sin D\\&=\displaystyle \frac{1}{2}\times 23\times 16\times \sin {{43}^\circ}\\&=125.49\ \text{c}{{\text{m}}^{2}}\end{align*}[/latex]

The area of parallelogram [latex]\scriptsize ABCD=2\times 125.49\ \text{c}{{\text{m}}^{2}}=250.98\ \text{c}{{\text{m}}^{2}}[/latex].

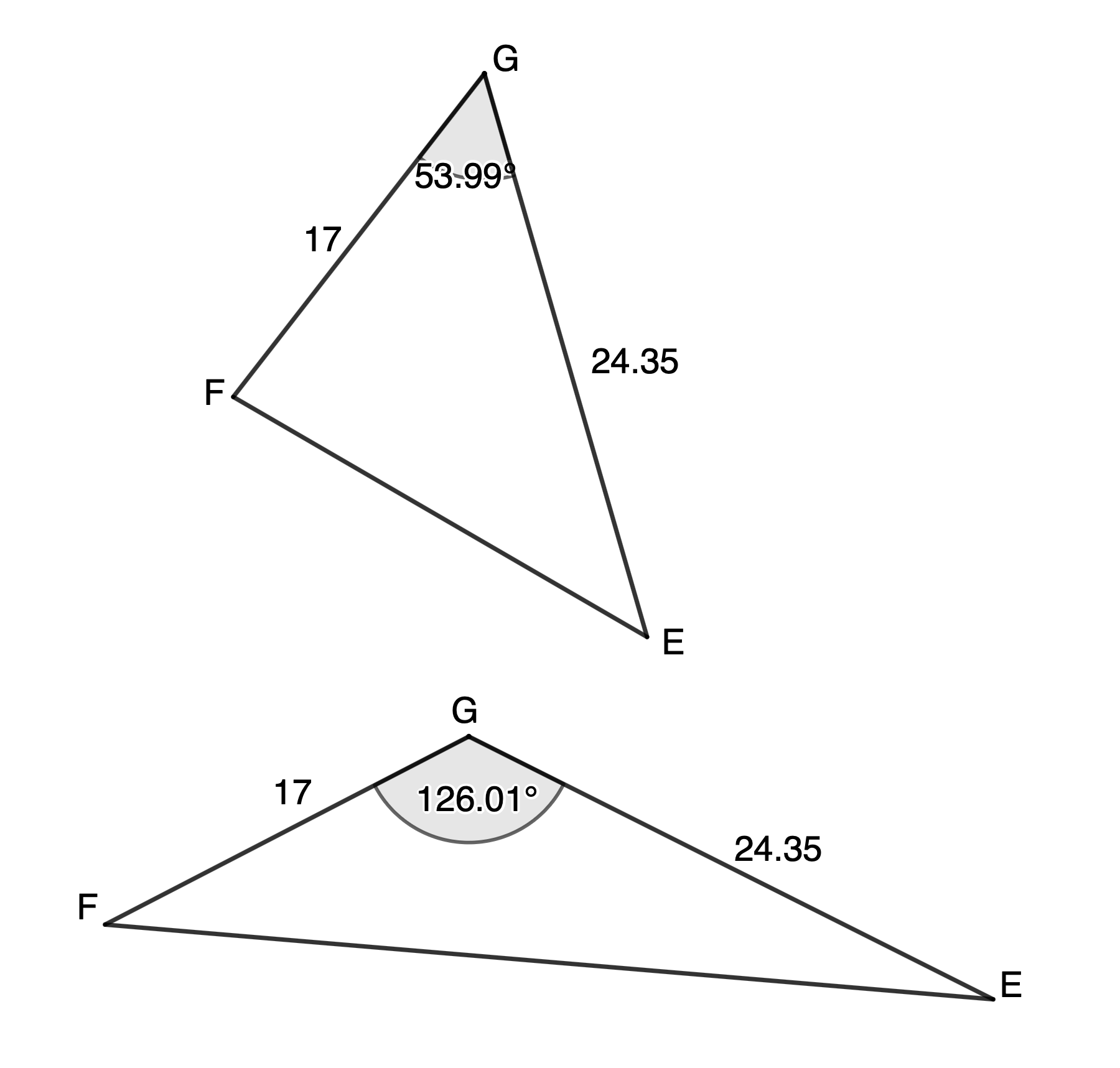
Example 5.4

If [latex]\scriptsize \Delta EFG[/latex] has an area of [latex]\scriptsize 167.43\ \text{c}{{\text{m}}^{2}}[/latex] and [latex]\scriptsize e=17\ \text{cm}[/latex] and [latex]\scriptsize f=24.35\ \text{cm}[/latex], what are the two possible sizes of [latex]\scriptsize \hat{G}[/latex], correct to two decimal places.

Solution

This question gives us the area and asks us to calculate the size of [latex]\scriptsize \hat{G}[/latex].

[latex]\scriptsize \begin{align*}\text{Area }\Delta EFG & =\displaystyle \frac{1}{2}ef\sin G\\\therefore 167.43 & =\displaystyle \frac{1}{2}\times 17\times 24.35\times \sin G\\\therefore \sin G & ={{53.99}^\circ}\end{align*}[/latex]

We have found that [latex]\scriptsize \hat{G}={{53.99}^\circ}[/latex] but the question mentions two possible solutions. Remember that sine is also positive in the second quadrant, in other words, for angles [latex]\scriptsize 90{}^\circ \le \theta \le {{180}^\circ}[/latex]. Therefore, [latex]\scriptsize \hat{G}={{180}^\circ}-{{53.99}^\circ}={{126.01}^\circ}[/latex] as well. But does this make physical sense? Does such a triangle exist? Figure 3 shows both possible triangles with these dimensions.

Exercise 5.1

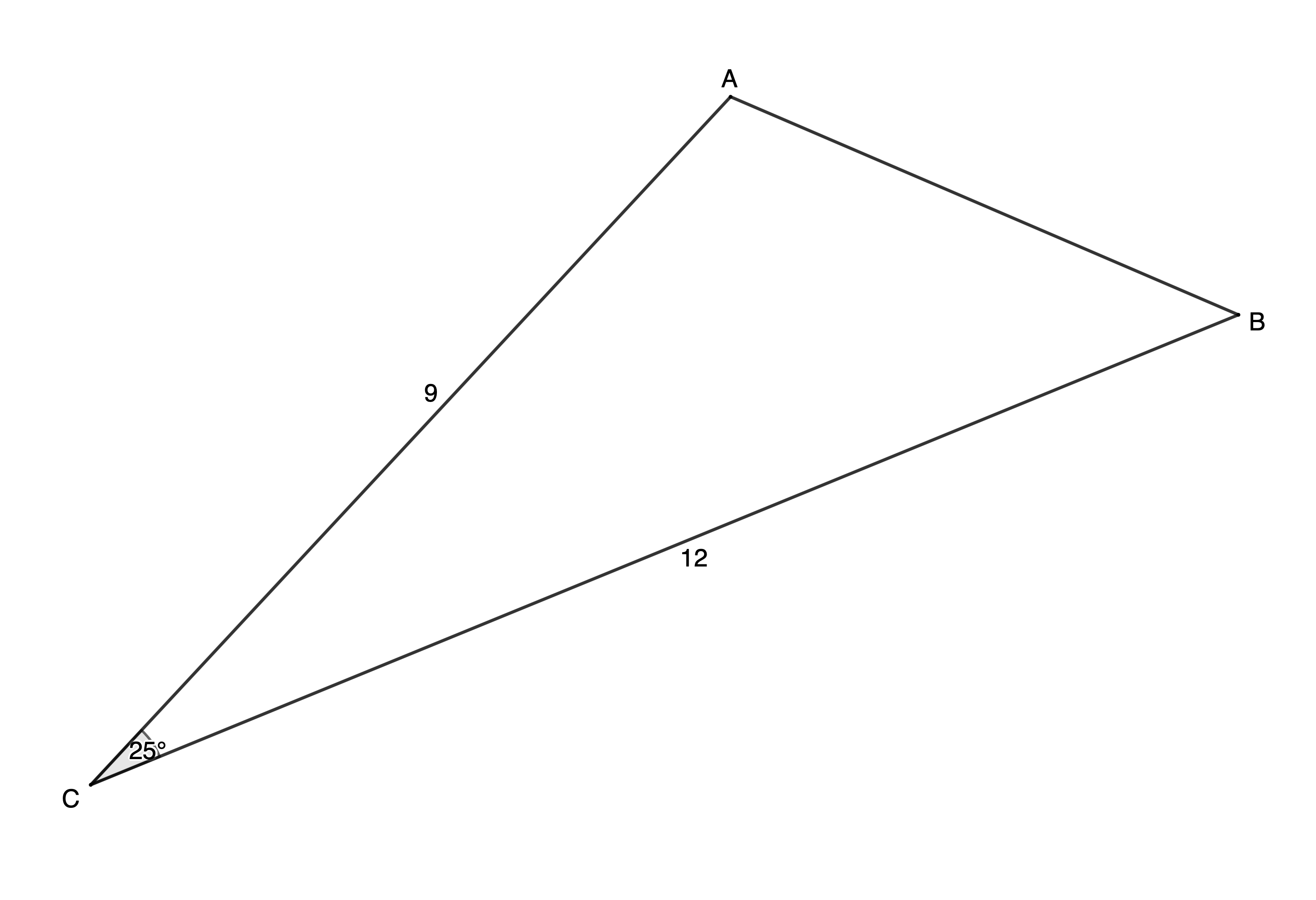
1. Calculate the area of [latex]\scriptsize \Delta ABC[/latex] to two decimal places.
   
2. Calculate the area of [latex]\scriptsize \Delta ABC[/latex] given [latex]\scriptsize a=10\ \text{cm}[/latex], [latex]\scriptsize c=8\ \text{cm}[/latex] and [latex]\scriptsize \hat{B}={{35}^\circ}[/latex], to three decimal places.
3. Determine the area of equilateral [latex]\scriptsize \Delta PQR[/latex] with [latex]\scriptsize p=14\ \text{cm}[/latex] to two decimal places.
4. Determine, to two decimal places, the area of a parallelogram in which two adjacent sides are [latex]\scriptsize 10\ \text{cm}[/latex] and [latex]\scriptsize 13\ \text{cm}[/latex] and the angle between them is [latex]\scriptsize {{55}^\circ}[/latex].
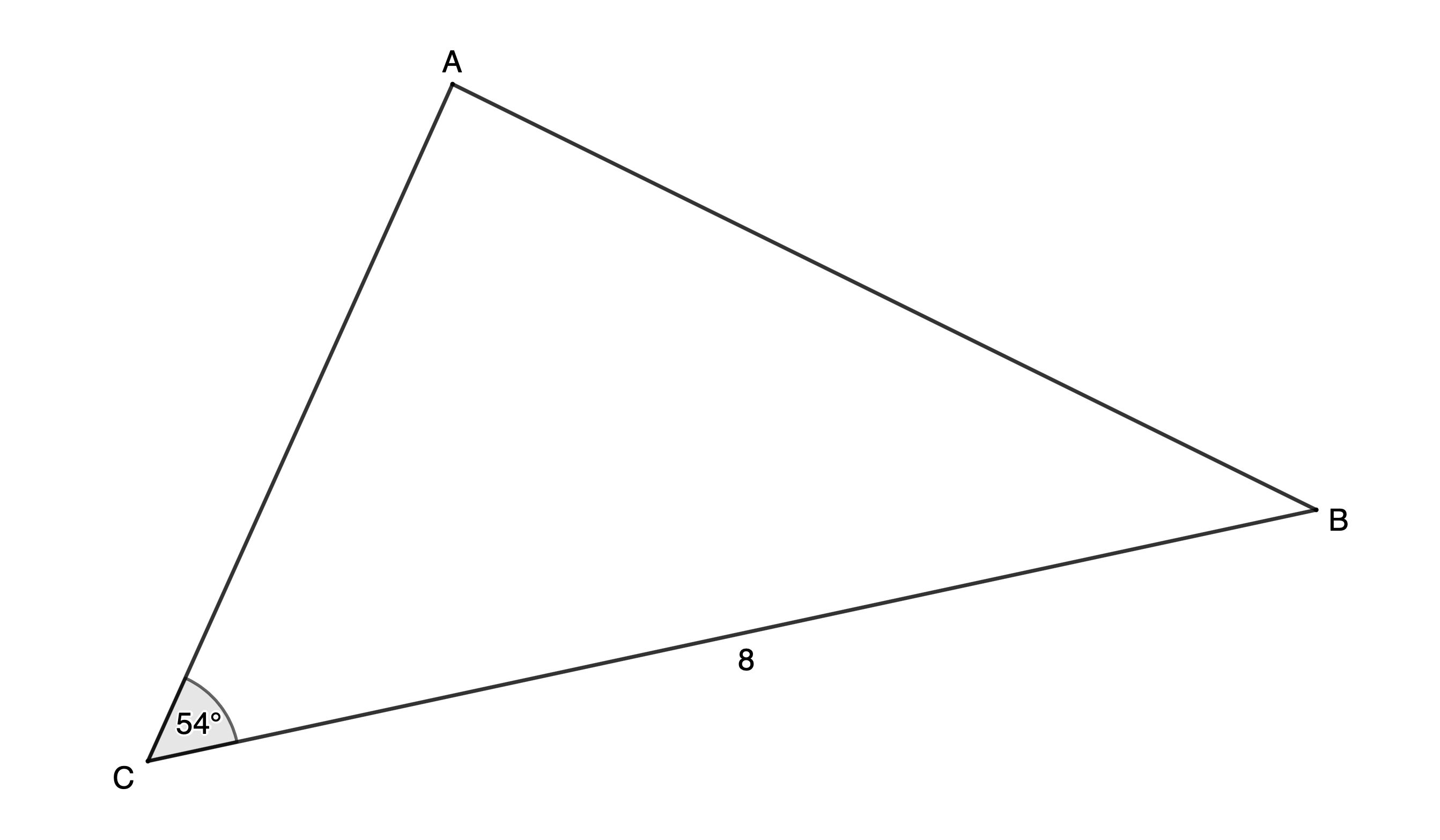
5. Determine the length of [latex]\scriptsize AC[/latex] (to one decimal place) if the area of [latex]\scriptsize \Delta ABC=16.18\ {{\text{m}}^{2}}[/latex].
   

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• What the area rule is.
  
• How to use the area rule to find the area of any triangle where two sides and the included angle are known.

Unit 5: Assessment

Suggested time to complete: 40 minutes

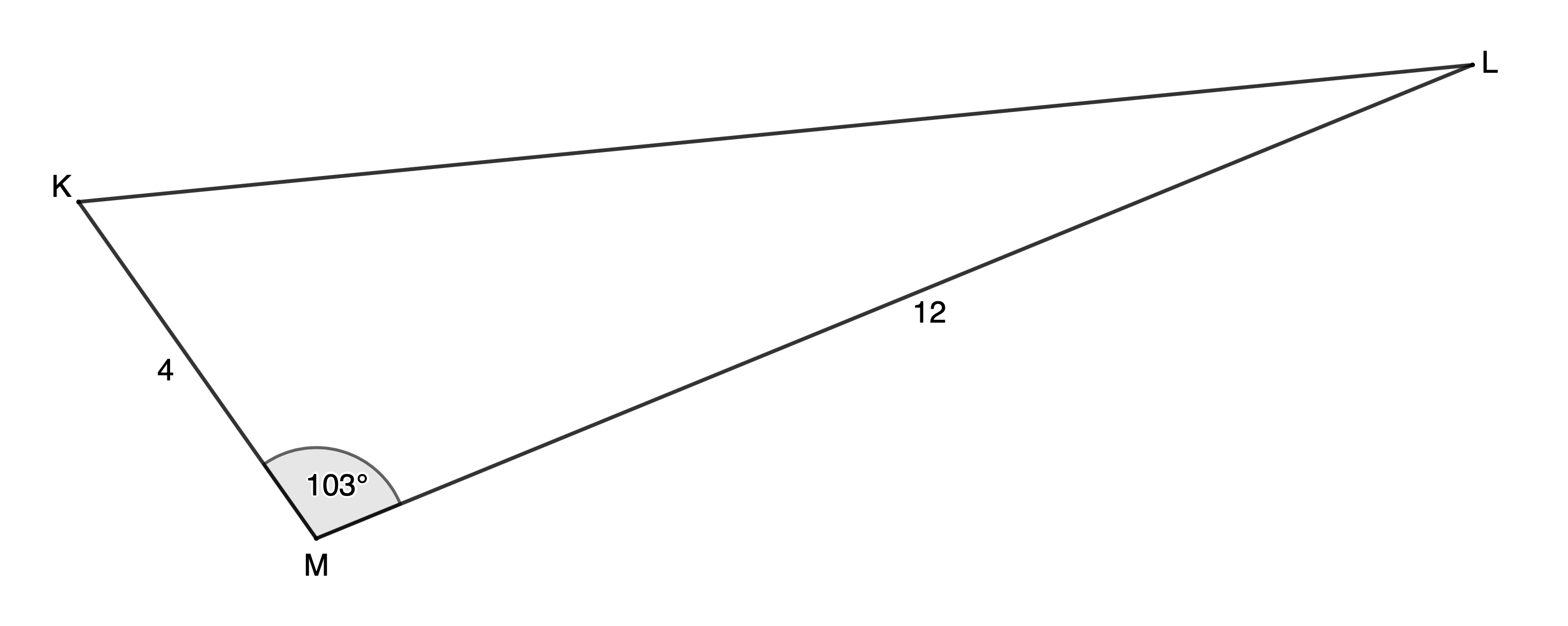
1. Calculate the area of [latex]\scriptsize \Delta KLM[/latex] to two decimal places.
   
2. Calculate, to two decimal places, the area of [latex]\scriptsize \Delta ABC[/latex] given [latex]\scriptsize b=19\ \text{cm}[/latex], [latex]\scriptsize c=18\ \text{cm}[/latex] and [latex]\scriptsize \hat{A}={{49}^\circ}[/latex].
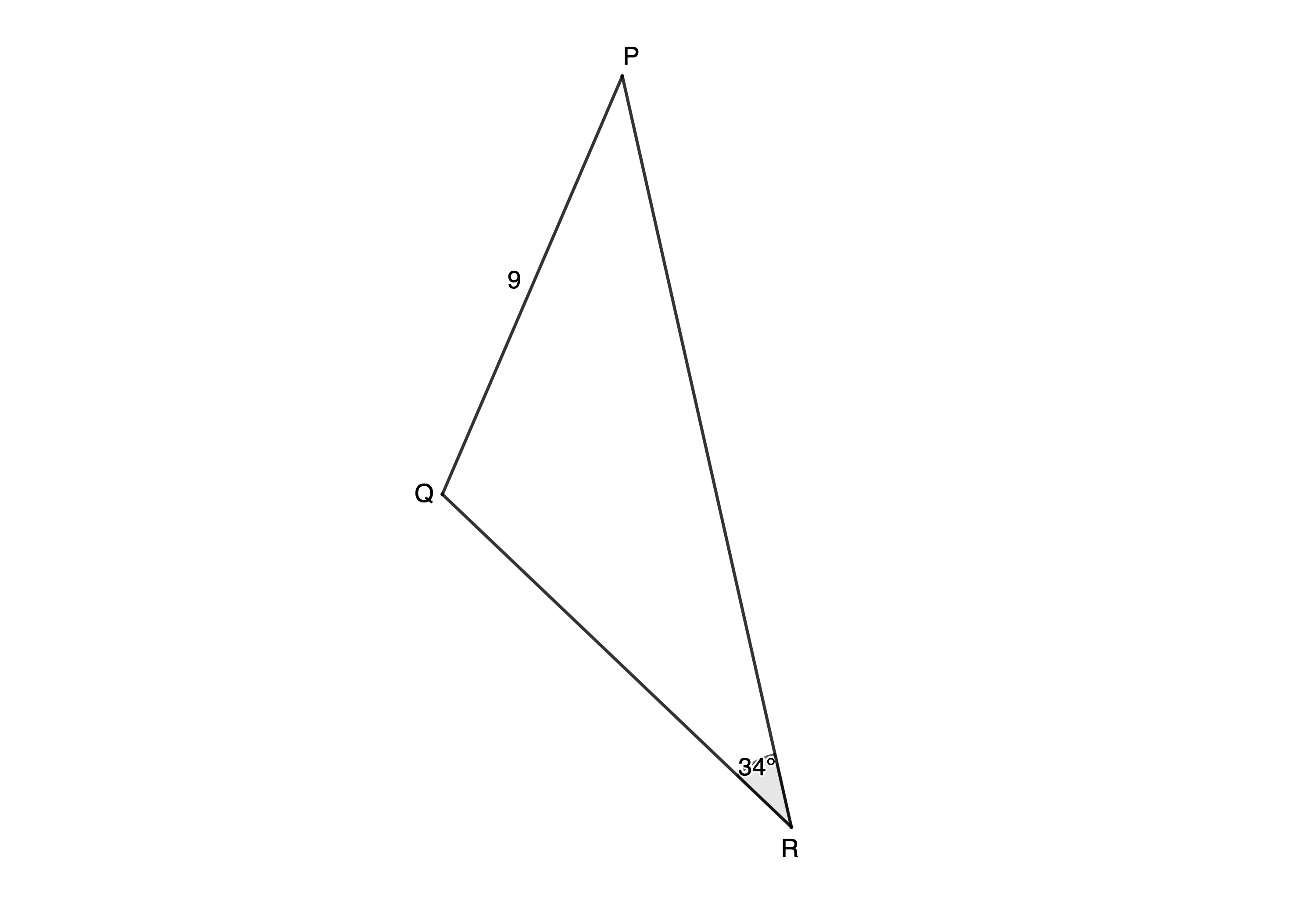
3. Determine, to two decimal places, the area of [latex]\scriptsize \Delta PQR[/latex] with [latex]\scriptsize p=r=9\ \text{m}[/latex].
   
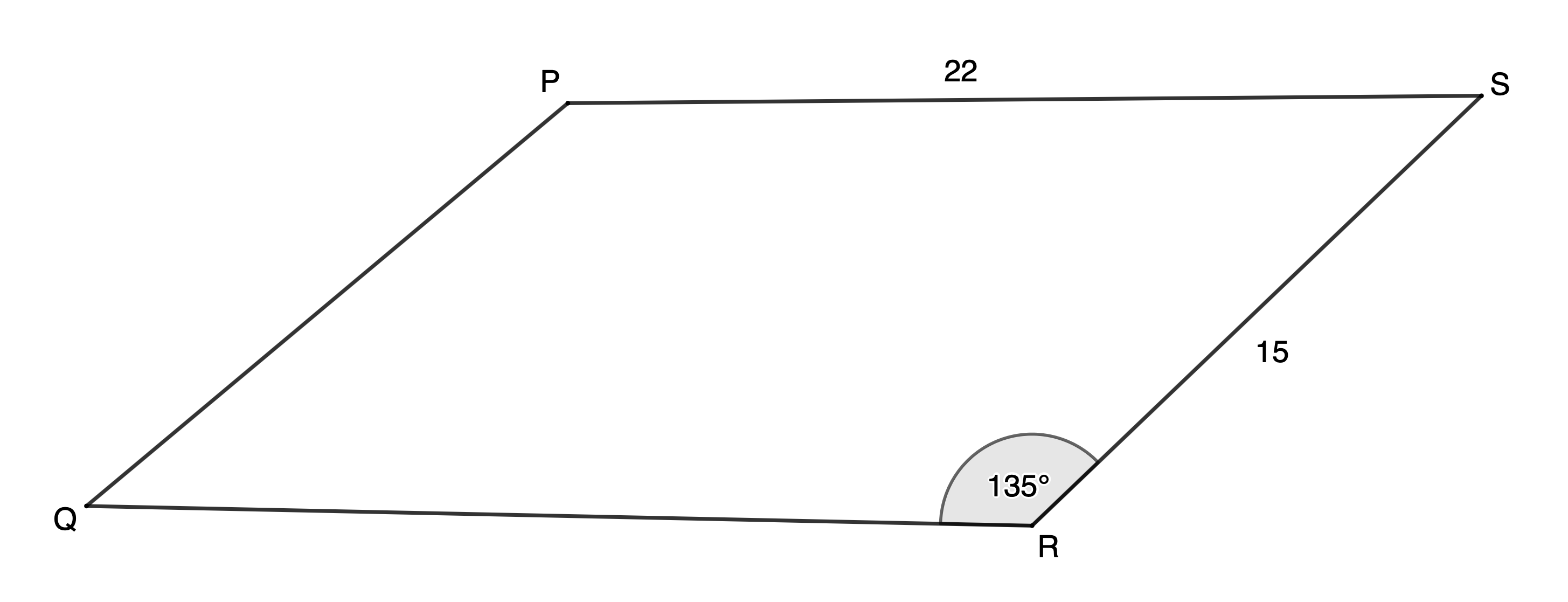
4. Determine the area of a parallelogram [latex]\scriptsize PQRS[/latex] to two decimal places.
   
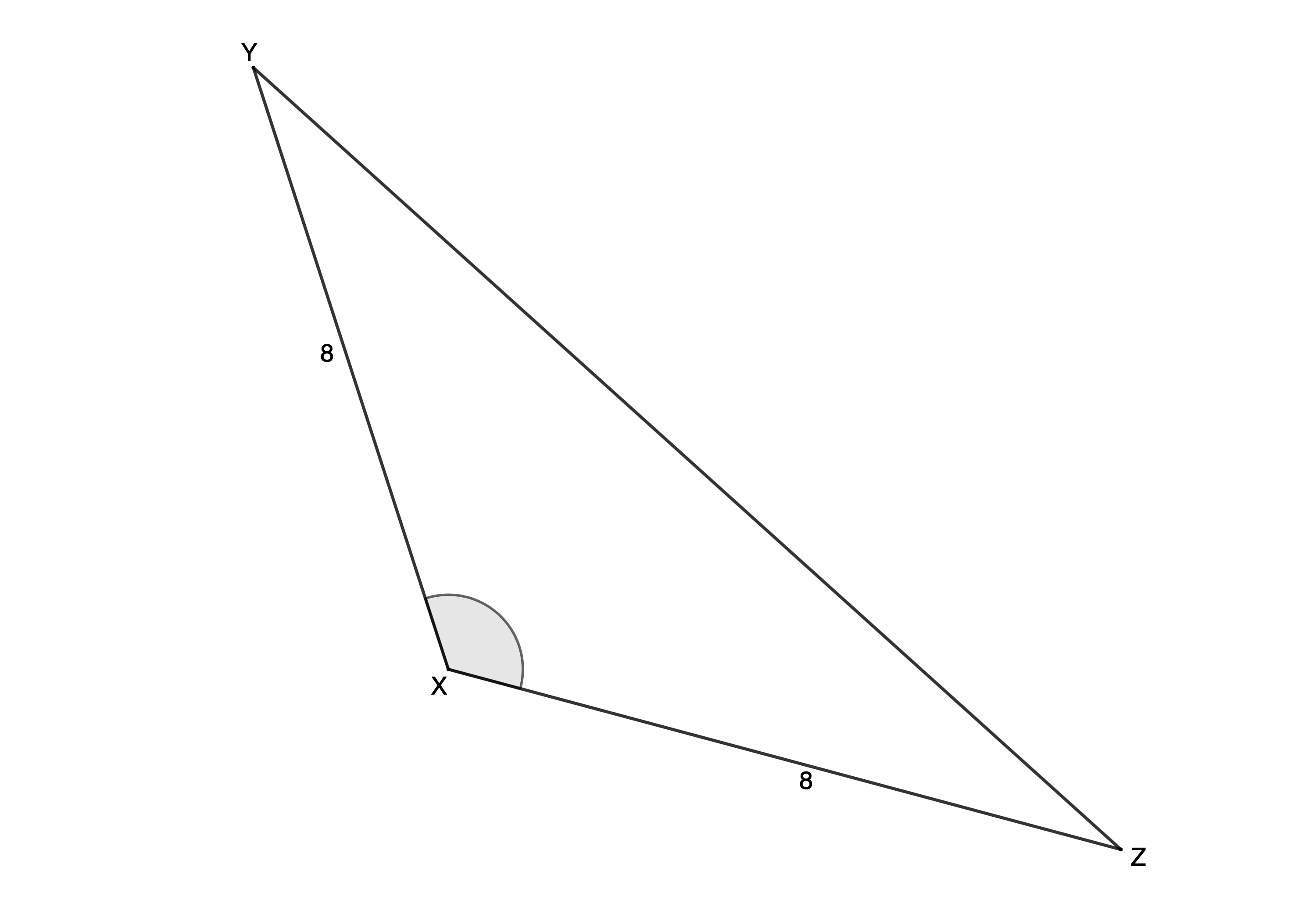
5. Determine two possible values for [latex]\scriptsize \hat{X}[/latex] (to one decimal place) if the area of [latex]\scriptsize \Delta XYZ=26.72\ {{\text{m}}^{2}}[/latex].
   

The full solutions are at the end of the unit.

Unit 5: Solutions

Exercise 5.1

1. .
   [latex]\scriptsize \begin{align*}\text{Area }\Delta ABC&=\displaystyle \frac{1}{2}ab\sin C\\&=\displaystyle \frac{1}{2}\times 12\times 9\times \sin {{25}^\circ}\\&=22.82\ {{\text{u}}^{2}}\end{align*}[/latex]
   Note: No units were given so we include [latex]\scriptsize {{\text{u}}^{2}}[/latex] for units squared.
2. .
   [latex]\scriptsize \begin{align*}\text{Area }\Delta ABC&=\displaystyle \frac{1}{2}ac\sin B\\&=\displaystyle \frac{1}{2}\times 10\times 8\times \sin {{35}^\circ}\\&=22.943\ \text{c}{{\text{m}}^{2}}\end{align*}[/latex]
3. [latex]\scriptsize \Delta PQR[/latex] is an equilateral triangle. Therefore, all three sides have length [latex]\scriptsize 14\ \text{cm}[/latex] and all three angles are [latex]\scriptsize {{60}^\circ}[/latex]. We can choose any combination of sides and angle.
   [latex]\scriptsize \begin{align*}\text{Area }\Delta ABC&=\displaystyle \frac{1}{2}pq\sin R\\&=\displaystyle \frac{1}{2}\times 14\times 14\times \sin {{60}^\circ}\\&=84.87\ \text{c}{{\text{m}}^{2}}\end{align*}[/latex]
4. .
   
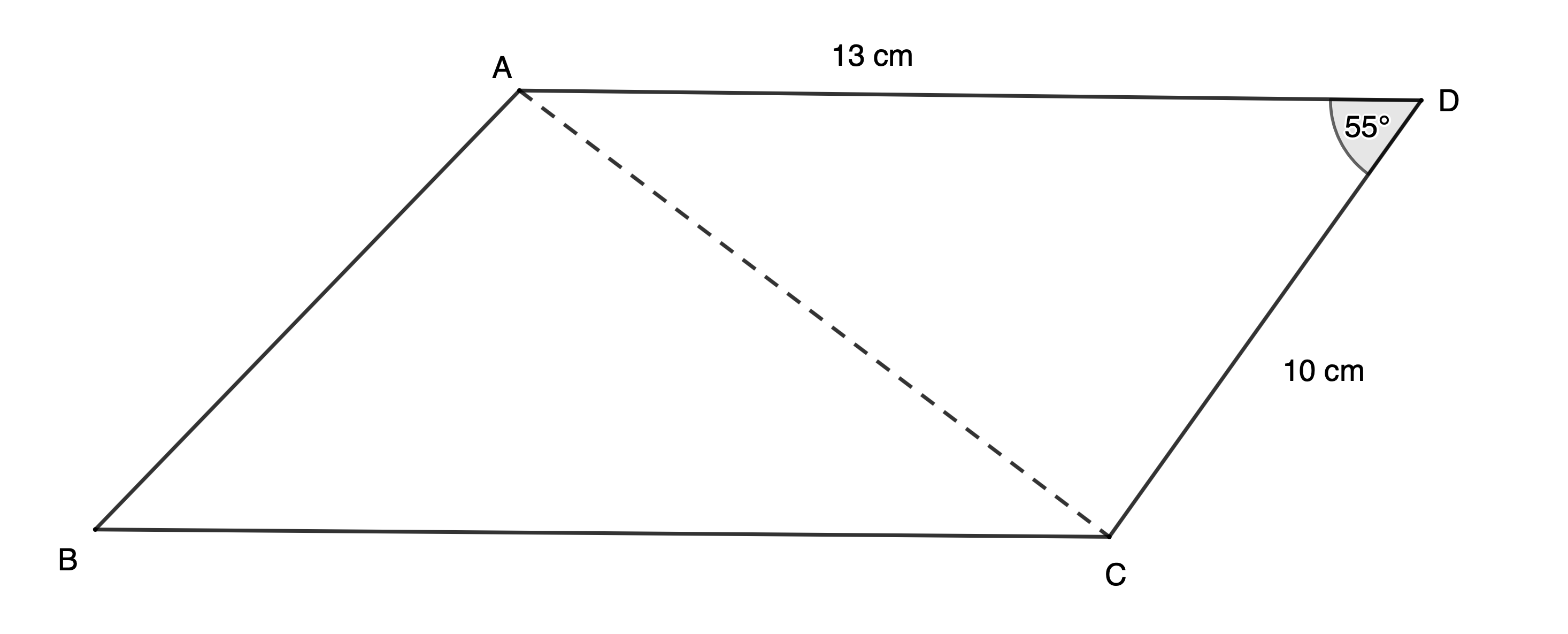
   [latex]\scriptsize \begin{align*}\text{Area }\Delta ACD&=\displaystyle \frac{1}{2}ac\sin D\\&=\displaystyle \frac{1}{2}\times 10\times 13\times \sin {{55}^\circ}\\&=53.24\ \text{c}{{\text{m}}^{2}}\end{align*}[/latex]
   Area of parallelogram [latex]\scriptsize ABCD=2\times 53.24\ \text{c}{{\text{m}}^{2}}=106.49\ \text{c}{{\text{m}}^{2}}[/latex]
5. .
   [latex]\scriptsize \begin{align*}\text{Area }\Delta ABC & =16.18\ {{\text{m}}^{2}}\\\therefore 16.18 & =\displaystyle \frac{1}{2}\times AC\times 8\times \sin {{54}^\circ}\\\therefore AC & =4.045\sin {{54}^\circ}\\\therefore AC & =3.3\ \text{m}\end{align*}[/latex]

Back to Exercise 5.1

Unit 5: Assessment

1. .
   [latex]\scriptsize \begin{align*}\text{Area }\Delta KLM&=\displaystyle \frac{1}{2}kl\sin M\\&=\displaystyle \frac{1}{2}\times 12\times 4\times \sin {{103}^\circ}\\&=23.38\ {{\text{u}}^{2}}\end{align*}[/latex]
2. .
   [latex]\scriptsize \begin{align*}\text{Area }\Delta ABC&=\displaystyle \frac{1}{2}bc\sin A\\&=\displaystyle \frac{1}{2}\times 19\times 18\times \sin {{49}^\circ}\\&=129.06\ \text{c}{{\text{m}}^{2}}\end{align*}[/latex]
3. [latex]\scriptsize PQ=RQ[/latex] (given)
   [latex]\scriptsize \therefore \hat{R}=\hat{P}={{34}^\circ}[/latex] (angles opposite equal sides)
   [latex]\scriptsize \begin{align*}\therefore \hat{Q} & ={{180}^\circ}-R-P\\ & ={{180}^\circ}-{{34}^\circ}-{{34}^\circ}\\ & ={{112}^\circ}\end{align*}[/latex] (angles in a triangle are supplementary)
   [latex]\scriptsize \begin{align*}\text{Area }\Delta PQR&=\displaystyle \frac{1}{2}pr\sin Q\\&=\displaystyle \frac{1}{2}\times 9\times 9\times \sin {{112}^\circ}\\&=37.55\ {{\text{m}}^{2}}\end{align*}[/latex]
4. [latex]\scriptsize PQRS[/latex] is a parallelogram (given)
   [latex]\scriptsize \therefore QR=PS=22[/latex] (opposite sides of parallelogram)
   
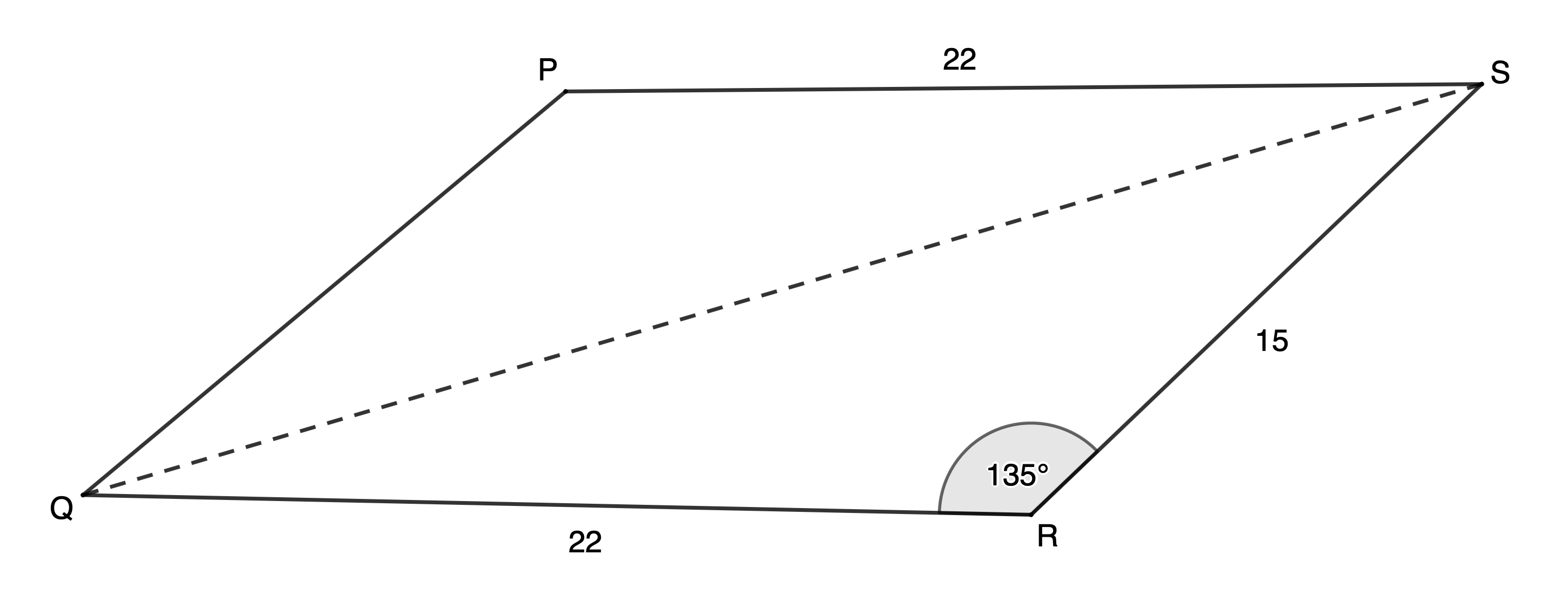
   [latex]\scriptsize \begin{align*}\text{Area }\Delta QRS&=\displaystyle \frac{1}{2}qs\sin R\\&=\displaystyle \frac{1}{2}\times 15\times 22\times \sin {{135}^\circ}\\&=116.67\ {{\text{u}}^{2}}\end{align*}[/latex]
   [latex]\scriptsize \text{Area }PQRS=2\times 116.67=233.35\ {{\text{u}}^{2}}[/latex](rounding off in the final step)
5. [latex]\scriptsize \text{Area }\Delta XYZ=26.72\ {{\text{m}}^{2}}[/latex]
   [latex]\scriptsize \begin{align*}\therefore 26.72 & =\displaystyle \frac{1}{2}yz\sin X\\ & =\displaystyle \frac{1}{2}\times 8\times 8\times \sin X\\\therefore \sin X & =0.835\\\therefore \hat{X} & ={{56.6}^\circ}\text{ or }\hat{X} & ={{180}^\circ}-{{56.62}^\circ}={{123.4}^\circ}\end{align*}[/latex]

Back to Unit 5: Assessment