Space, shape and measurement: Use the Cartesian co-ordinate system to derive and apply equations
Unit 3: Determine the angle of inclination of a line
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Use the gradient of a straight line to determine the angle of inclination of the line with the x-axis.
- Use the angle of inclination to determine the gradient of a straight line.
What you should know
Before you start this unit, make sure you can:
- Define the tangent ratio.
- Use a calculator to determine the tangent of an angle.
- Use a calculator to determine the angle from a given tangent ratio.
- Use the CAST diagram to identify where tangent is positive and negative.
Refer to level 2 subject outcome 3.6 unit 1 if you need help with any of this.
Introduction
So far in this subject outcome we have been calculating the gradients of straight lines using the idea of a gradient being [latex]\scriptsize \displaystyle \frac{{\text{rise}}}{{\text{run}}}[/latex] – the vertical distance between two points on the straight line divided by the horizontal distance between those points. This idea leads us to an equation for gradient that we know well: [latex]\scriptsize m=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}[/latex].
However, there is another way in which we can measure the gradient of a straight line on the Cartesian plane and this is to measure the angle that the line makes with the x-axis. This is called the angle of inclination.
The angle of inclination
Figure 1 shows what we mean by the angle of inclination. It is the angle that a straight line makes with the positive x-axis.
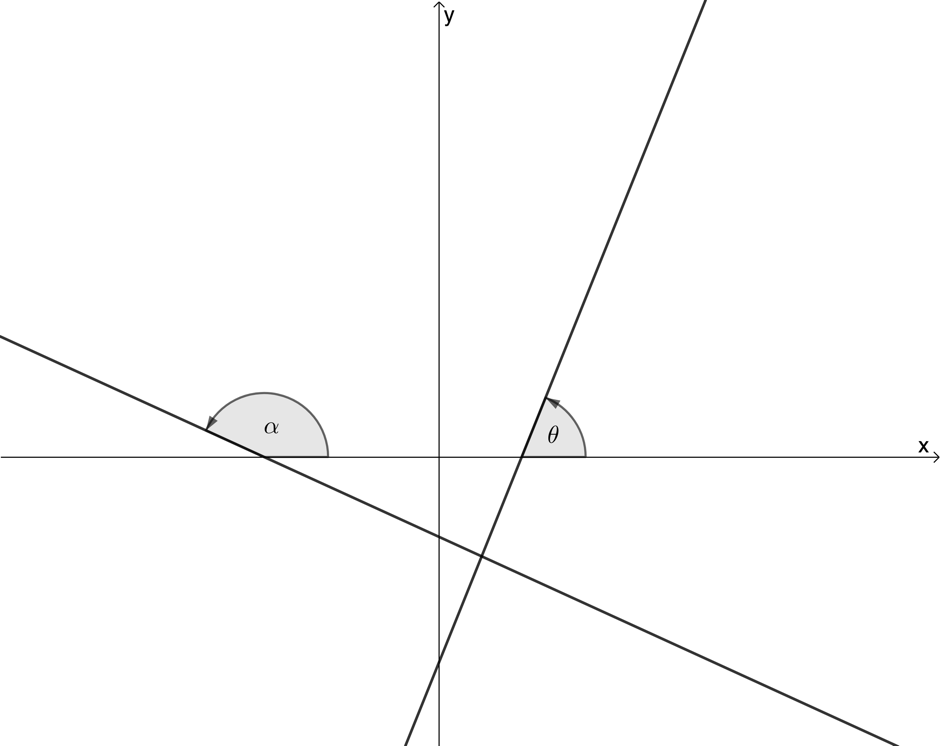
Notice how we always measure the angle of inclination in an anti-clockwise direction from the more positive side of the x-axis of where the line intersects with it.
This means that:
- the angle of inclination is always [latex]\scriptsize {{0}^\circ}\le \theta \le {{180}^\circ}[/latex]
- positive gradients have an angle of inclination [latex]\scriptsize {{0}^\circ} \lt \theta \lt {{90}^\circ}[/latex]
- negative gradients have an angle of inclination [latex]\scriptsize {{90}^\circ} \lt \theta \lt {{180}^\circ}[/latex].
As the gradient of the straight line changes, so does its angle of inclination. If you have an internet connection visit this practical example.
Here you will find a slider with which to change the gradient of the line. Change the gradient to see how this affects the angle of inclination of the straight line.
We know that [latex]\scriptsize m=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{\Delta y}}{{\Delta x}}[/latex] or the change in [latex]\scriptsize y[/latex] divided by the change in [latex]\scriptsize x[/latex]. However, if you look at Figure 2, you will see that, with respect to the angle of inclination, [latex]\scriptsize \theta[/latex], [latex]\scriptsize \Delta y[/latex] is the opposite side of the triangle and [latex]\scriptsize \Delta x[/latex] is the adjacent side.
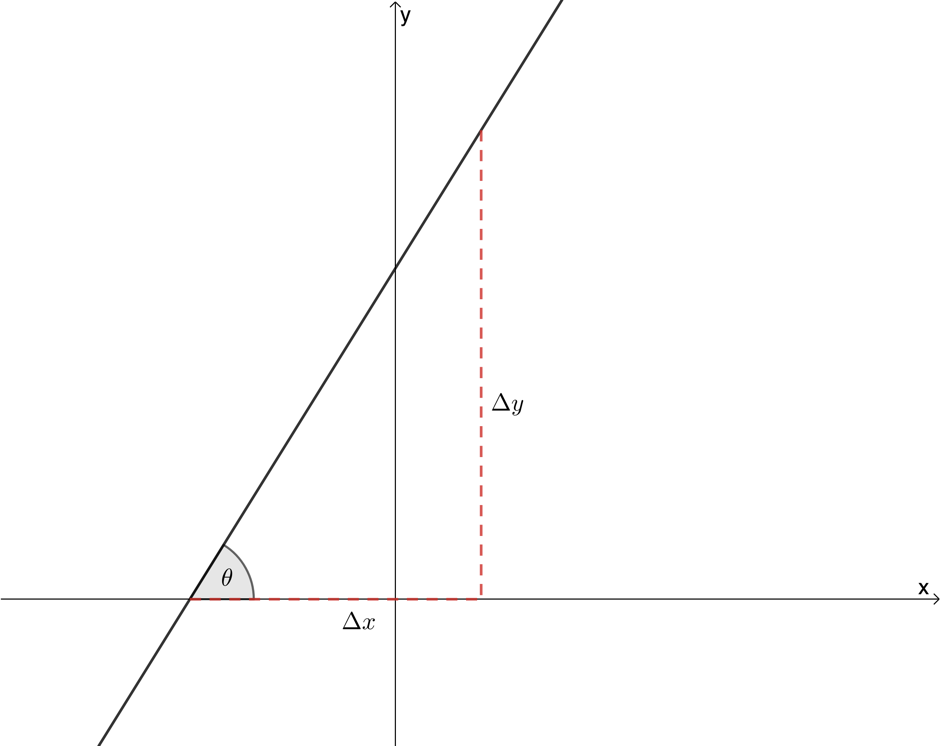
Therefore, we can say that [latex]\scriptsize \tan \theta =\displaystyle \frac{{\text{opposite}}}{{\text{adjacent}}}=\displaystyle \frac{{\Delta y}}{{\Delta x}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=m[/latex]. In other words, [latex]\scriptsize \tan \theta =m[/latex] for [latex]\scriptsize {{0}^\circ}\le \theta \le {{180}^\circ}[/latex].
We know that the tangent function is positive in the first quadrant ([latex]\scriptsize {{0}^\circ} \lt \theta \lt {{90}^\circ}[/latex]) and negative in the second quadrant ([latex]\scriptsize {{90}^\circ} \lt \theta \lt {{180}^\circ}[/latex]). So, it makes sense that lines with an angle of inclination [latex]\scriptsize {{0}^\circ} \lt \theta \lt {{90}^\circ}[/latex] have a positive gradient and lines with an angle of inclination [latex]\scriptsize {{90}^\circ} \lt \theta \lt {{180}^\circ}[/latex] have a negative gradient.
Angle of inclination and gradient:
[latex]\scriptsize m=\tan \theta[/latex]
Example 3.1
Determine the gradient of a straight line with an angle of inclination of:
- [latex]\scriptsize {{63}^\circ}[/latex]
- [latex]\scriptsize {{107}^\circ}[/latex]
Solution
We know that [latex]\scriptsize m=\tan \theta[/latex]. Therefore, we need to use a calculator to determine the gradient in each case.
[latex]\scriptsize \tan {{63}^\circ}=1.96[/latex]
[latex]\scriptsize \tan {{107}^\circ}=-3.27[/latex]
We can see that the angle of inclination [latex]\scriptsize {{0}^\circ} \lt \theta \lt {{90}^\circ}[/latex] results in a positive gradient, while the angle of inclination [latex]\scriptsize {{90}^\circ} \lt \theta \lt {{180}^\circ}[/latex] results in a negative gradient.
Example 3.2
Determine the angle of inclination of a straight line with a gradient of:
- [latex]\scriptsize m=\displaystyle \frac{3}{7}[/latex]
- [latex]\scriptsize m=-\displaystyle \frac{4}{3}[/latex]
Solution
We know that [latex]\scriptsize m=\tan \theta[/latex] but in this case, we have been given [latex]\scriptsize m[/latex] and we need to use a calculator to determine the angle of inclination, [latex]\scriptsize \theta[/latex]. So, we need to use the [latex]\scriptsize {{\tan }^{{-1}}}[/latex] button on our calculator.
[latex]\scriptsize \begin{align*}\tan \theta & =\displaystyle \frac{3}{7}\\\therefore \theta & ={{23.20}^\circ}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\tan \theta & =-\displaystyle \frac{4}{3}\\\therefore \theta & =-{{53.13}^\circ}\end{align*}[/latex]
In this case, the calculator gives an angle in the fourth quadrant. We need to add [latex]\scriptsize {{180}^\circ}[/latex] to put the angle into the second quadrant.
[latex]\scriptsize \theta =-{{53.13}^\circ}+{{180}^\circ}={{126.87}^\circ}[/latex]
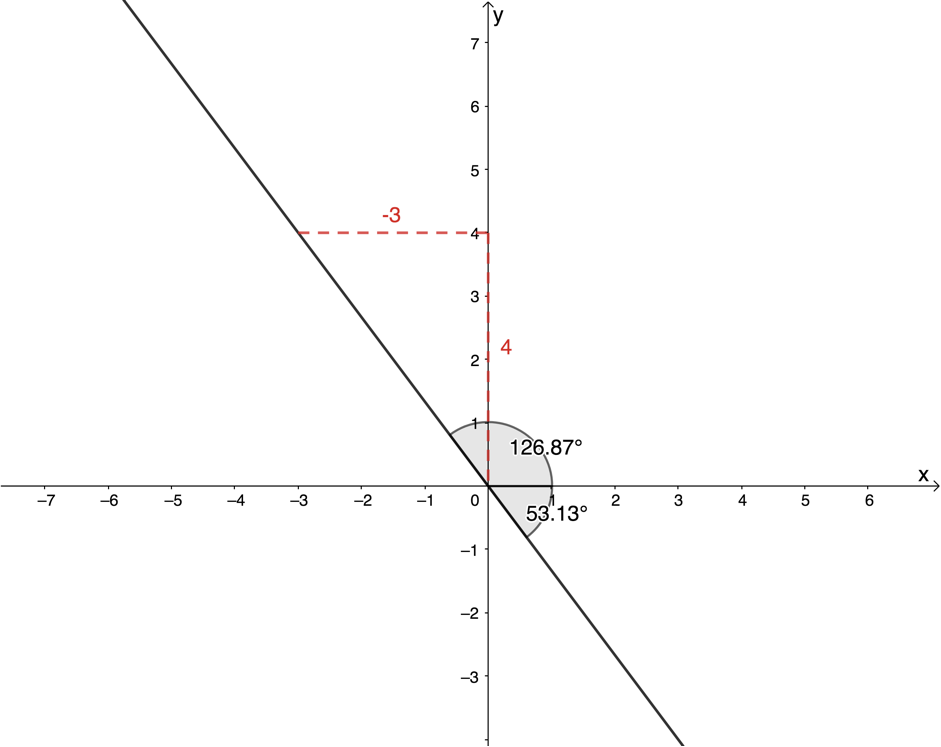
We can see that positive gradients give angles of inclination [latex]\scriptsize {{0}^\circ} \lt \theta \lt {{90}^\circ}[/latex] while negative gradients give angles of inclination [latex]\scriptsize {{90}^\circ} \lt \theta \lt {{180}^\circ}[/latex].
Exercise 3.1
- Determine the gradient (correct to two decimal places) of straight lines with the following angles of inclination:
- [latex]\scriptsize {{60}^\circ}[/latex]
- [latex]\scriptsize {{50}^\circ}[/latex]
- [latex]\scriptsize {{152}^\circ}[/latex]
- [latex]\scriptsize {{0}^\circ}[/latex]
- [latex]\scriptsize {{180}^\circ}[/latex]
- [latex]\scriptsize {{90}^\circ}[/latex]
- Determine the angle of inclination (to two decimal places) of the following straight lines:
- [latex]\scriptsize 3x+2y-6=0[/latex]
- [latex]\scriptsize \displaystyle \frac{1}{2}y-x=3[/latex]
- The line passing through [latex]\scriptsize (2,-3)[/latex] and [latex]\scriptsize (4,7)[/latex]
- [latex]\scriptsize y=6[/latex]
- [latex]\scriptsize x=\sqrt{3}[/latex]
The full solutions are at the end of the unit.
Example 3.3
Determine the equation of the straight line passing through [latex]\scriptsize (\displaystyle \frac{1}{2},\displaystyle \frac{1}{4})[/latex] and perpendicular to a line with an angle of inclination of [latex]\scriptsize {{71.57}^\circ}[/latex].
Solution
The angle of inclination of the other line is [latex]\scriptsize {{71.57}^\circ}[/latex]. Therefore, we can find its gradient.
[latex]\scriptsize \tan {{71.57}^\circ}=3[/latex]
[latex]\scriptsize {{m}_{1}}=3[/latex]. Therefore, [latex]\scriptsize {{m}_{2}}=-\displaystyle \frac{1}{3}[/latex]
[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-\displaystyle \frac{1}{4} & =-\displaystyle \frac{1}{3}\left( {x-\displaystyle \frac{1}{2}} \right)\\\therefore y-\displaystyle \frac{1}{4} & =-\displaystyle \frac{1}{3}x+\displaystyle \frac{1}{6}\\\therefore y & =-\displaystyle \frac{1}{3}x+\displaystyle \frac{{2+3}}{{12}}\\y&=-\displaystyle \frac{1}{3}x+\displaystyle \frac{5}{{12}}\end{align*}[/latex]
Exercise 3.2
Determine the equation of the straight line perpendicular to the line with an angle of inclination of [latex]\scriptsize {{165.964}^\circ}[/latex] and passing through the point [latex]\scriptsize (-1,2)[/latex].
The full solution is at the end of the unit.
Example 3.4
Determine the acute angle (correct to one decimal place) between the line passing through [latex]\scriptsize (-2,4)[/latex] and [latex]\scriptsize (4,-2)[/latex] and the straight line [latex]\scriptsize y=3x+2[/latex].
Solution
It will help to draw a sketch of the situation. We can see the angle of inclination of each line ([latex]\scriptsize \theta[/latex] and [latex]\scriptsize \alpha[/latex]) and that the acute angle between the two lines is [latex]\scriptsize \beta[/latex]. If we find [latex]\scriptsize \theta[/latex] and [latex]\scriptsize \alpha[/latex], we can find [latex]\scriptsize \beta[/latex] using angles in a triangle.
[latex]\scriptsize y=3x+2[/latex]. Therefore, [latex]\scriptsize m=3[/latex].
[latex]\scriptsize \begin{align*}\tan \theta & =3\\\therefore \theta & ={{71.57}^\circ}\end{align*}[/latex]
[latex]\scriptsize m=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{4-(-2)}}{{-2-4}}=\displaystyle \frac{6}{{-6}}=-1[/latex]
[latex]\scriptsize \begin{align*}\tan \alpha & =-1\\\therefore \alpha & ={{135}^\circ}\end{align*}[/latex]
So, the angle next to [latex]\scriptsize \alpha[/latex] inside the triangle is [latex]\scriptsize {{45}^\circ}[/latex] (angles on a straight line are supplementary).
[latex]\scriptsize \beta ={{180}^\circ}-{{45}^\circ}-{{71.57}^\circ}={{63.43}^\circ}[/latex] (angles inside a triangle are supplementary).
Exercise 3.3
Determine the angle between the straight lines [latex]\scriptsize y=-x+3[/latex] and [latex]\scriptsize y-x=\displaystyle \frac{1}{2}[/latex]. What can you say about these two straight lines?
The full solution is at the end of the unit.
Summary
In this unit you have learnt the following:
- The angle of inclination, [latex]\scriptsize \theta[/latex], is the angle made between a straight line and the positive x-axis.
- The angle of inclination is always [latex]\scriptsize {{0}^\circ}\le \theta \le {{180}^\circ}[/latex].
- Gradient [latex]\scriptsize m=\tan \theta[/latex].
- Positive gradients have an angle of inclination [latex]\scriptsize {{0}^\circ}\le \theta \le {{90}^\circ}[/latex].
- Negative gradients have an angle of inclination [latex]\scriptsize {{90}^\circ}\le \theta \le {{180}^\circ}[/latex].
Unit 3: Assessment
Suggested time to complete: 50 minutes
Question 1 is adapted from NC(V) Mathematics Level 3 Paper 2 November 2014 question 1.3
- In the diagram below [latex]\scriptsize A(4,3)[/latex], [latex]\scriptsize B(2,7)[/latex], [latex]\scriptsize C(-2,5)[/latex] and [latex]\scriptsize D(0,1)[/latex] are four points on the Cartesian plane.
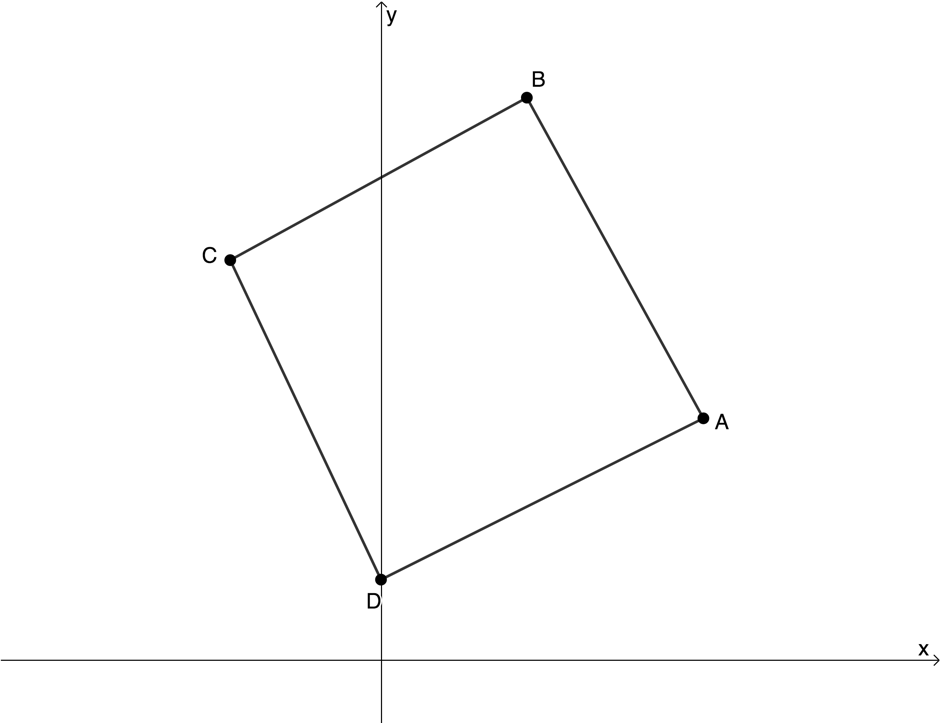
- Calculate the length of [latex]\scriptsize BD[/latex] (leaving the answer in the simplest surd form if necessary).
- Show that [latex]\scriptsize CA=BD[/latex].
- Calculate the co-ordinates of [latex]\scriptsize M[/latex] , the midpoint of [latex]\scriptsize BD[/latex].
- Prove that [latex]\scriptsize AM\bot BD[/latex].
- What is the name given to quadrilateral [latex]\scriptsize ABCD[/latex]? Give a reason for your answer.
Question 2 is adapted from NC(V) Mathematics Level 3 Paper 2 November 2016 question 1.3
- In the diagram below, [latex]\scriptsize \displaystyle \Delta PQR[/latex] has vertices [latex]\scriptsize P(-2,-4)[/latex], [latex]\scriptsize Q(-4,2)[/latex]and [latex]\scriptsize R(7,-1)[/latex]. The angle of inclination of [latex]\scriptsize QP[/latex] is [latex]\scriptsize \theta[/latex].
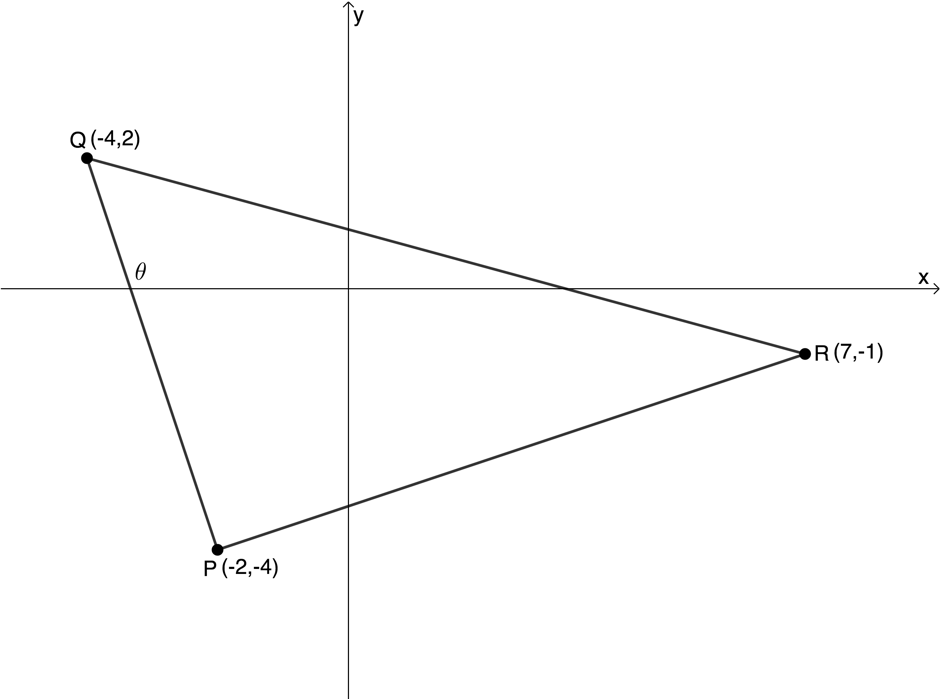
- Determine the coordinates of [latex]\scriptsize M[/latex], the midpoint of [latex]\scriptsize QR[/latex].
- Prove that [latex]\scriptsize QP\bot PR[/latex].
- Calculate the size of [latex]\scriptsize \theta[/latex] to the nearest degree.
Question 3 is adapted from Everything Maths Grade 11 Exercise 4-9 question 3
- [latex]\scriptsize P(2,3)[/latex], [latex]\scriptsize Q(-4,0)[/latex] and [latex]\scriptsize R(5,-3)[/latex] are the vertices of [latex]\scriptsize \Delta PQR[/latex] in the Cartesian plane. [latex]\scriptsize PR[/latex] intersects the x-axis at [latex]\scriptsize S[/latex].
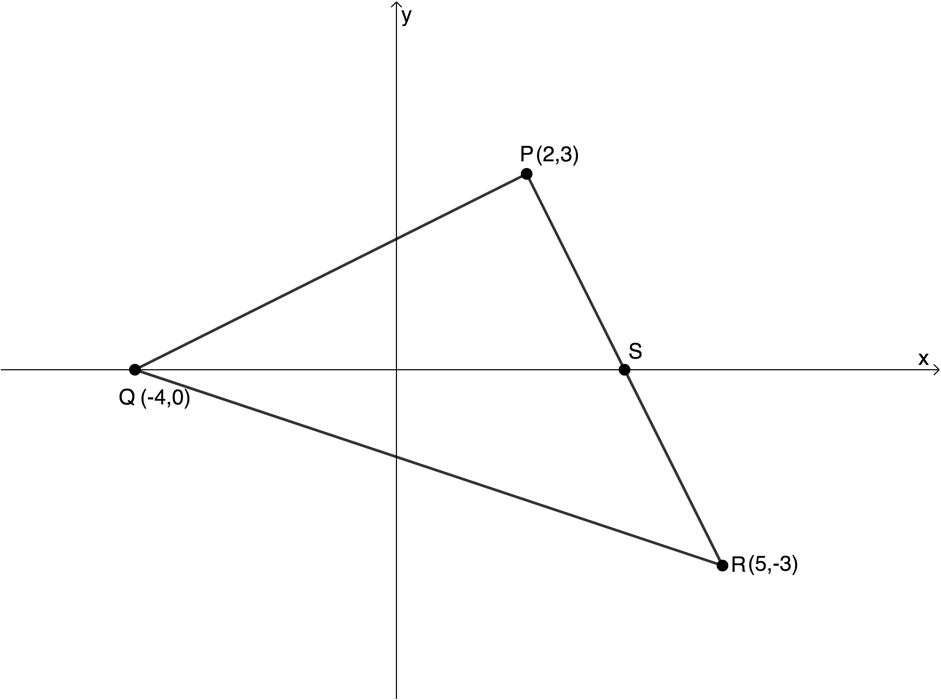
Determine the following:- The equation of the line [latex]\scriptsize PR[/latex].
- The coordinates of point [latex]\scriptsize S[/latex].
- The angle of inclination of [latex]\scriptsize PR[/latex] (correct to two decimal places).
- The gradient of line [latex]\scriptsize PQ[/latex].
- [latex]\scriptsize Q\hat{P}R[/latex].
- The equation of the line perpendicular to [latex]\scriptsize PQ[/latex] and passing through the origin.
- The mid-point [latex]\scriptsize M[/latex] of [latex]\scriptsize QR[/latex].
- The equation of the line parallel to [latex]\scriptsize PR[/latex] and passing through point [latex]\scriptsize M[/latex].
Question 4 is adapted from Everything Maths Grade 11 Exercise 4-9 question 8
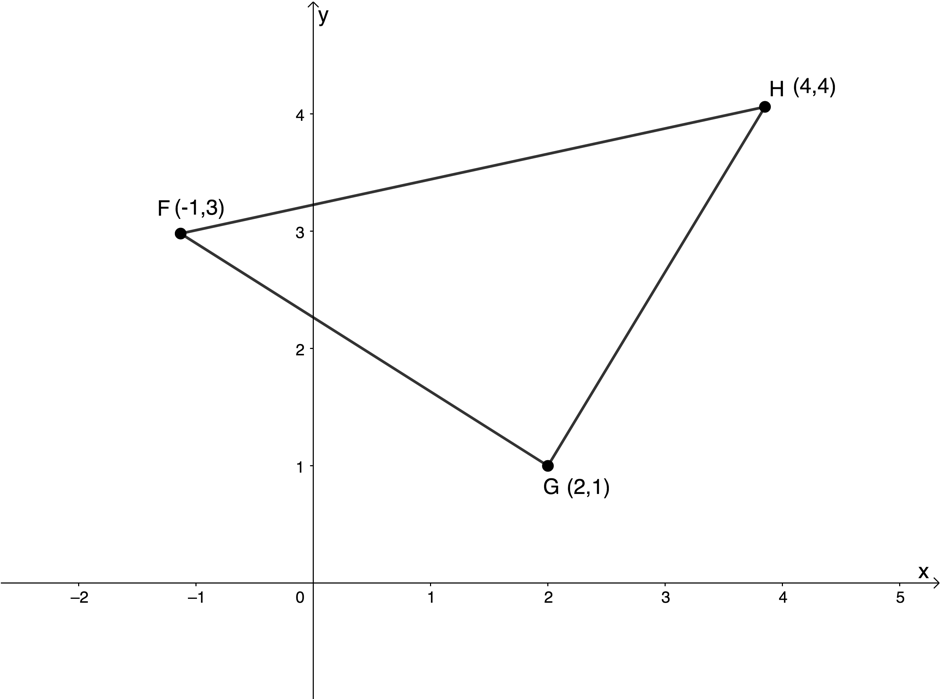
- Consider triangle [latex]\scriptsize FGH[/latex] with vertices [latex]\scriptsize F(-1,3)[/latex], [latex]\scriptsize G(2,1)[/latex] and [latex]\scriptsize H(4,4)[/latex].
- Sketch [latex]\scriptsize \Delta FGH[/latex] on the Cartesian plane.
- Show that [latex]\scriptsize \Delta FGH[/latex] is an isosceles triangle.
- Determine the equation of the line [latex]\scriptsize PQ[/latex], the perpendicular bisector of [latex]\scriptsize FH[/latex].
- Does [latex]\scriptsize G[/latex] lie on the line [latex]\scriptsize PQ[/latex]?
- Determine the equation of the line parallel to [latex]\scriptsize GH[/latex] and passing through point [latex]\scriptsize F[/latex].
The full solutions are at the end of the unit.
Unit 3: Solutions
Exercise 3.1
- .
- [latex]\scriptsize \tan {{60}^\circ}=1.73[/latex]. Therefore, [latex]\scriptsize m=1.73[/latex].
- [latex]\scriptsize \tan {{50}^\circ}=1.19[/latex]. Therefore, [latex]\scriptsize m=1.19[/latex].
- [latex]\scriptsize \tan {{152}^\circ}=-0.53[/latex]. Therefore, [latex]\scriptsize m=-0.53[/latex].
- [latex]\scriptsize \tan {{0}^\circ}=0[/latex]. Therefore, [latex]\scriptsize m=0[/latex].
- [latex]\scriptsize \tan {{180}^\circ}=0[/latex]. Therefore, [latex]\scriptsize m=0[/latex].
- [latex]\scriptsize \tan {{90}^\circ}[/latex] is undefined. Therefore [latex]\scriptsize m[/latex] is undefined, and the line is vertical.
- .
- .
[latex]\scriptsize \begin{align*} 3x+2y-6&=0\\ \therefore 2y&=-3x+6\\ \therefore y&=-\displaystyle \frac{3}{2}x+3 \end{align*}[/latex]
[latex]\scriptsize m=-\displaystyle \frac{3}{2}[/latex]
[latex]\scriptsize \begin{align*}\tan \theta &=-\displaystyle \frac{3}{2}\\\therefore \theta &=-{{56.31}^\circ}\end{align*}[/latex]
But we need the second quadrant angle. Therefore, [latex]\scriptsize \theta =-{{56.31}^\circ}+{{180}^\circ}={{123.69}^\circ}[/latex]. - .
[latex]\scriptsize \begin{align*}\displaystyle \frac{1}{2}y-x & =3\\\therefore \displaystyle \frac{1}{2}y & =x+3\\\therefore y & =2x+6\end{align*}[/latex]
[latex]\scriptsize m=2[/latex]
[latex]\scriptsize \begin{align*}\tan \theta &=2\\\therefore \theta &={{63.43}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize m=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{7-(-3)}}{{4-2}}=\displaystyle \frac{{10}}{2}=5[/latex]
[latex]\scriptsize \begin{align*}\tan \theta &=5\\\therefore \theta &={{78.69}^\circ}\end{align*}[/latex] - [latex]\scriptsize m=0[/latex]. Therefore, [latex]\scriptsize \theta ={{0}^\circ}[/latex]
- [latex]\scriptsize m[/latex] is undefined. Therefore [latex]\scriptsize \theta ={{90}^\circ}[/latex]
- .
Exercise 3.2
[latex]\scriptsize \begin{align*}{{m}_{1}} & =\tan {{165.964}^\circ}\\\therefore {{m}_{1}} & =-0.25=-\displaystyle \frac{1}{4}\end{align*}[/latex]
[latex]\scriptsize {{m}_{2}}=4[/latex]
[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-2 & =4\left( {x-(-1)} \right)\\\therefore y-2 & =4(x+1)\\\therefore y-2 & =4x+4\\\therefore y & =4x+6\end{align*}[/latex]
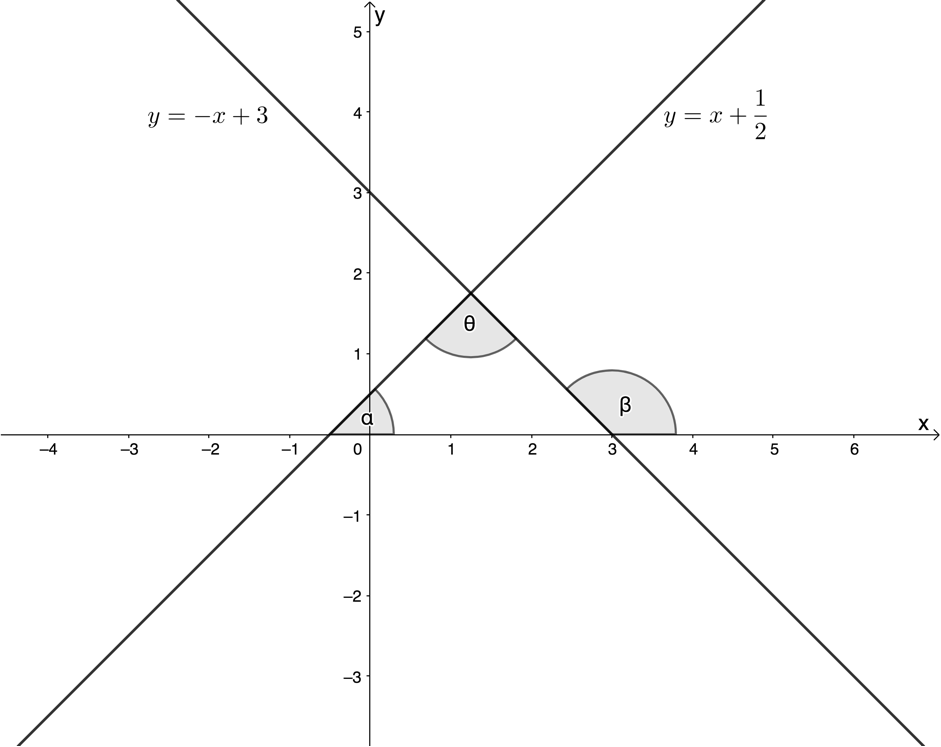
[latex]\scriptsize y=-x+3[/latex]
[latex]\scriptsize m=-1[/latex]
[latex]\scriptsize \begin{align*}\tan \beta & =-1\\\therefore \beta & ={{135}^\circ}\end{align*}[/latex]
Therefore, the angle next to [latex]\scriptsize \beta[/latex] inside the triangle is [latex]\scriptsize {{45}^\circ}[/latex] (angles on straight line are supplementary).
[latex]\scriptsize \begin{align*}y-x & =\displaystyle \frac{1}{2}\\\therefore y & =x+\displaystyle \frac{1}{2}\end{align*}[/latex]
[latex]\scriptsize m=1[/latex]
[latex]\scriptsize \begin{align*}\tan \alpha &=1\\\therefore \alpha &={{45}^\circ}\end{align*}[/latex]
[latex]\scriptsize \theta ={{180}^\circ}-{{45}^\circ}-{{45}^\circ}={{90}^\circ}[/latex]
The two straight lines are perpendicular.
Unit 3: Assessment
- .
- .
[latex]\scriptsize \begin{align*} BD&=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\\ &=\sqrt{\left(0-2\right)^2+\left(1-7\right)^2}\\ &=\sqrt{2^{2}+6^{2}}\\ &=\sqrt{4+36}\\ &=\sqrt{40}\\ &=2\sqrt{10} \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}CA&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{(-2-4)}}^{2}}+{{{(5-3)}}^{2}}}}\\&=\sqrt{{{{{(-6)}}^{2}}+{{2}^{2}}}}\\&=\sqrt{{36+4}}\\&=\sqrt{{40}}\\&=2\sqrt{{10}}\end{align*}[/latex]
[latex]\scriptsize CA=BD[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{{M}_{{BD}}}&=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\\&=\left( {\displaystyle \frac{{2+0}}{2},\displaystyle \frac{{7+1}}{2}} \right)\\&=\left( {\displaystyle \frac{2}{2},\displaystyle \frac{8}{2}} \right)\\&=(1,4)\end{align*}[/latex] - [latex]\scriptsize A(4,3)[/latex], [latex]\scriptsize M(1,4)[/latex]
[latex]\scriptsize {{m}_{{AM}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{4-3}}{{1-4}}=-\displaystyle \frac{1}{3}[/latex]
[latex]\scriptsize {{m}_{{BD}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{1-7}}{{0-2}}=\displaystyle \frac{6}{2}=3[/latex]
[latex]\scriptsize {{m}_{{AM}}}\times {{m}_{{BD}}}=-1[/latex]. Therefore [latex]\scriptsize AM\bot BD[/latex]. - [latex]\scriptsize ABCD[/latex] is a rhombus. The diagonals bisect at [latex]\scriptsize {{90}^\circ}[/latex].
- .
- .
- .
[latex]\scriptsize \begin{align*}{{M}_{{QR}}}&=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\\&=\left( {\displaystyle \frac{{7-4}}{2},\displaystyle \frac{{-1+2}}{2}} \right)\\&=\left( {\displaystyle \frac{3}{2},\displaystyle \frac{1}{2}} \right)\end{align*}[/latex] - [latex]\scriptsize \displaystyle {{m}_{{QP}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{-4-2}}{{-2-(-4)}}=\displaystyle \frac{{-6}}{{-2+4}}=-\displaystyle \frac{6}{2}=-3[/latex]
[latex]\scriptsize \displaystyle {{m}_{{PR}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{-1-(-4)}}{{7-(-2)}}=\displaystyle \frac{{-1+4}}{{7+2}}=\displaystyle \frac{3}{9}=\displaystyle \frac{1}{3}[/latex]
[latex]\scriptsize {{m}_{{QP}}}\times {{m}_{{PR}}}=-1[/latex]. Therefore, [latex]\scriptsize QP\bot PR[/latex]. - .
[latex]\scriptsize \begin{align*}\tan \theta & ={{m}_{{QP}}}=-3\\\therefore \theta & ={{108}^\circ}\end{align*}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{y-{{y}_{1}}}}{{x-{{x}_{1}}}} & =\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}\\\therefore \displaystyle \frac{{y-3}}{{x-2}} & =\displaystyle \frac{{-3-3}}{{5-2}}\\\therefore \displaystyle \frac{{y-3}}{{x-2}} & =-\displaystyle \frac{6}{3}=-2\\\therefore y-3 & =-2(x-2)\\\therefore y-3 & =-2x+4\\\therefore y & =-2x+7\end{align*}[/latex] - [latex]\scriptsize S[/latex] is the x-axis intercept of the line segment [latex]\scriptsize PR[/latex].
x-intercept (let [latex]\scriptsize y=0[/latex]):
[latex]\scriptsize \begin{align*}0&=-2x+7\\\therefore 2x&=7\\\therefore x&=\displaystyle \frac{7}{2}\end{align*}[/latex]
[latex]\scriptsize S(\displaystyle \frac{7}{2},0)[/latex] - .
[latex]\scriptsize \begin{align*}{{m}_{{PR}}} & =-2=\tan \theta \\\therefore \theta & ={{116.57}^\circ}\end{align*}[/latex] - [latex]\scriptsize {{m}_{{PQ}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{0-3}}{{-4-2}}=\displaystyle \frac{{-3}}{{-6}}=\displaystyle \frac{1}{2}[/latex]
- [latex]\scriptsize {{m}_{{PR}}} =-2[/latex], [latex]\scriptsize m_{PQ}=\displaystyle \frac{1}{2}[/latex]
[latex]\scriptsize {{m}_{{PR}}}\times {{m}_{{PQ}}}=-1[/latex]. Therefore, [latex]\scriptsize P\hat{Q}R={{90}^\circ}[/latex] - [latex]\scriptsize {{m}_{{PQ}}}=\displaystyle \frac{1}{2}[/latex]. Therefore, gradient of the line is [latex]\scriptsize \displaystyle \frac{1}{2}[/latex].
Equation of the line is [latex]\scriptsize y=\displaystyle \frac{1}{2}x[/latex] - .
[latex]\scriptsize \begin{align*}{{M}_{{QR}}}&=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\\&=\left( {\displaystyle \frac{{5-4}}{2},\displaystyle \frac{{-3+0}}{2}} \right)\\&=\left( {\displaystyle \frac{1}{2},-\displaystyle \frac{3}{2}} \right)\end{align*}[/latex] - [latex]\scriptsize {{m}_{{PR}}} =-2[/latex], [latex]\scriptsize (\displaystyle \frac{1}{2},-\displaystyle \frac{3}{2})[/latex]
[latex]\scriptsize \begin{align*}y-{{y}_{1}}&=m(x-{{x}_{1}})\\\therefore y-\left( {-\displaystyle \frac{3}{2}} \right)&=-2\left( {x-\displaystyle \frac{1}{2}} \right)\\\therefore y+\displaystyle \frac{3}{2}&=-2x+1\\\therefore y&=-2x-\displaystyle \frac{1}{2}\end{align*}[/latex]
- .
- Consider triangle [latex]\scriptsize FGH[/latex] with vertices [latex]\scriptsize F(-1,3)[/latex], [latex]\scriptsize G(2,1)[/latex] and [latex]\scriptsize H(4,4)[/latex].
- .
- .
[latex]\scriptsize \displaystyle \begin{align*}FG&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{\left( {2-(-1)} \right)}}^{2}}+{{{\left( {1-3} \right)}}^{2}}}}\\&=\sqrt{{{{{\left( 3 \right)}}^{2}}+{{{\left( 2 \right)}}^{2}}}}\\&=\sqrt{{9+4}}\\&=\sqrt{{13}}\end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}GH&=\sqrt{{{{{({{x}_{2}}-{{x}_{1}})}}^{2}}+{{{({{y}_{2}}-{{y}_{1}})}}^{2}}}}\\&=\sqrt{{{{{\left( {4-1} \right)}}^{2}}+{{{\left( {4-2} \right)}}^{2}}}}\\&=\sqrt{{{{{\left( 3 \right)}}^{2}}+{{{\left( 2 \right)}}^{2}}}}\\&=\sqrt{{9+4}}\\&=\sqrt{{13}}\end{align*}[/latex]
[latex]\scriptsize FG=GH[/latex]. Therefore, [latex]\scriptsize \Delta FGH[/latex] is an isosceles triangle. - .
[latex]\scriptsize \begin{align*}{{M}_{{FH}}}&=\left( {\displaystyle \frac{{{{x}_{1}}+{{x}_{2}}}}{2},\displaystyle \frac{{{{y}_{1}}+{{y}_{2}}}}{2}} \right)\\&=\left( {\displaystyle \frac{{4-1}}{2},\displaystyle \frac{{4+3}}{2}} \right)\\&=\left( {\displaystyle \frac{3}{2},\displaystyle \frac{7}{2}} \right)\end{align*}[/latex]
[latex]\scriptsize {{m}_{{FH}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{4-3}}{{4-(-1)}}=\displaystyle \frac{1}{5}[/latex]
[latex]\scriptsize {{m}_{{PQ}}}=-5[/latex] and [latex]\scriptsize PQ[/latex] passes through [latex]\scriptsize M(\displaystyle \frac{3}{2},\displaystyle \frac{7}{2})[/latex].
[latex]\scriptsize \displaystyle \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-\displaystyle \frac{7}{2} & =-5\left( {x-\displaystyle \frac{3}{2}} \right)\\\therefore y-\displaystyle \frac{7}{2} & =-5x+\displaystyle \frac{{15}}{2}\\\therefore y & =-5x+\displaystyle \frac{{22}}{2}\\y & =-5x+11\end{align*}[/latex] - [latex]\scriptsize G(2,1)[/latex]. If [latex]\scriptsize G[/latex] lies on [latex]\scriptsize PQ[/latex], [latex]\scriptsize G[/latex] will satisfy the equation of [latex]\scriptsize PQ[/latex].
[latex]\scriptsize y=-5x+11[/latex]
Substitute the x-coordinate from [latex]\scriptsize G(2,1)[/latex] into the equation of [latex]\scriptsize PQ[/latex]:
[latex]\scriptsize \begin{align*}\text{y} & =-2(5)+11\\ & =-10+11\\ & =1\end{align*}[/latex]
The x- and y-coordinates of [latex]\scriptsize G[/latex] satisfy the equation of [latex]\scriptsize PQ[/latex]. Therefore [latex]\scriptsize G[/latex] lies on [latex]\scriptsize PQ[/latex]. - [latex]\scriptsize {{m}_{{GH}}}=\displaystyle \frac{{{{y}_{2}}-{{y}_{1}}}}{{{{x}_{2}}-{{x}_{1}}}}=\displaystyle \frac{{4-1}}{{4-2}}=\displaystyle \frac{3}{2}[/latex]
Therefore, gradient of the line passing through [latex]\scriptsize F(-1,3)[/latex] is [latex]\scriptsize \displaystyle \frac{3}{2}[/latex].
[latex]\scriptsize \begin{align*}y-{{y}_{1}} & =m(x-{{x}_{1}})\\\therefore y-3 & =\displaystyle \frac{3}{2}\left( {x-(-1)} \right)\\\therefore y-3 & =\displaystyle \frac{3}{2}x+\displaystyle \frac{3}{2}\\\therefore y & =\displaystyle \frac{3}{2}x+\displaystyle \frac{9}{2}\end{align*}[/latex]
- .
Media Attributions
- figure1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example3.2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentQ1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentQ2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentQ3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise3.3A1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentA4a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
