Unit outcomes

By the end of this unit you will be able to:

• Use the compound growth formula (or compound interest formula) to solve problems related to finance.
• Solve for [latex]\scriptsize A,P[/latex] and [latex]\scriptsize i[/latex] using the compound interest formula.

What you should know

Before you start this unit, make sure that you can:

• Use a scientific calculator. Look back to level 2 subject outcome 1.1 to revise this.
• Use basic laws of arithmetic.
• Solve simple equations. Level 2 subject outcome 2.2 unit 1 will provide help with these.
• Complete basic simple interest calculations. Refer to level 2 subject outcome 5.2 unit 1 for help with this.

Introduction

Simple and compound growth formulae are used most commonly when talking about financial loans and investments. Growth is calculated as ‘interest’ on an amount that is invested or borrowed for a period of time, and added to the investment or loan, so that it grows bigger. In this unit we will look at compound interest and how it is calculated.

Calculating compound interest

The elements of the compound growth formula are as follows:

See how this formula differs from that for simple interest, where [latex]\scriptsize n[/latex], the time period, is not in the exponent. Simple interest formula: [latex]\scriptsize A=P(1+i.n)[/latex].

With compound growth, interest is calculated on the sum of the principal and the interest accumulated in the previous time periods. The interest is repeatedly calculated on an increasing amount. Unless stated otherwise, interest is compounded annually (i.e. added each year to the existing sum of principal and accumulated interest).

Let’s look at a few of the same examples from unit 1, but this time, learning how to use this compound interest formula.

Example 2.1

A TV costs [latex]\scriptsize \text{R}4\text{ 500}[/latex] on a hire purchase loan agreement. The interest charged is [latex]\scriptsize 12\%[/latex] compound interest each year (or per annum, ‘p.a.’) based on the full purchase price of the TV. Portia repays the loan over three years.

1. Calculate the full amount of money that is paid for the TV.
2. Calculate how much must be paid each month if equal payments are made every month.

Solution

Remember to list all the information given so you can identify what variable must be calculated.

[latex]\scriptsize \begin{align*}P&=4\text{ }500\\i&=12\%\\n&=3\\A&=?\end{align*}[/latex]

1. .
   [latex]\scriptsize \displaystyle \begin{align*}A&=P{{(1+i)}^{n}}\\ &=4\text{ }500{{\left( {1+\displaystyle \frac{{12}}{{100}}} \right)}^{3}}\\ &=4\text{ }500{{(1+0.12)}^{3}}\\ &=4\text{ }500{{(1.12)}^{3}}\\ &=4\text{ }500(1.405)&& \text{This is the answer of }{{1.12}^{3}}\text{, correct to 3 decimal places}\\ &=\text{R}6\text{ }322.18&& \text{The more accurate form of }{{1.12}^{3}}\text{ is used for the calculation, with }\\ &&& \text{rounding off done only in the final answer}\end{align*}[/latex]
   A total of [latex]\scriptsize \text{R}6\text{ 322}\text{.18}[/latex] is paid over the period of three years or [latex]\scriptsize 36[/latex] months.
   .
   Note: If you compare the amount calculated as compound interest here to that for simple interest, as calculated in example 1.1 in unit 1 ([latex]\scriptsize \text{R}6\text{ 120}[/latex]), you will see that the compound interest total is greater.
2. Each monthly payment should be [latex]\scriptsize \displaystyle \frac{{6\text{ }322.18}}{{36}}=\text{R}175.62[/latex]

Example 2.2

Pumla borrows [latex]\scriptsize \text{R}175\text{ 000}[/latex]to start a business and repays the loan in one lump sum after six years. The total amount that she is required to pay is [latex]\scriptsize \text{R}354\text{ 775}\text{.14}[/latex]. If the interest on the loan was compound interest, calculate the annual interest rate.

Solution

[latex]\scriptsize \begin{align*}P&=175\text{ }000\\A&=354\text{ }775.14\\n&=6\\i&=?\end{align*}[/latex]

[latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{6}}\\\displaystyle \frac{A}{P}&={{(1+i)}^{6}}\\\sqrt[6]{{\displaystyle \frac{A}{P}}}&=1+i\\\sqrt[6]{{\displaystyle \frac{A}{P}}}-1&=i\\i&=\sqrt[6]{{\displaystyle \frac{{354\text{ }775.14}}{{175\text{ }000}}}}-1\\&=\sqrt[6]{{2.0273}}-1\\&=1.125-1\\&=0.125\text{ or 12}\text{.5 }\% \text{ }\end{align*}[/latex]

Note: To avoid round-off errors, it is a good idea to do the calculation as one complete process on your calculator, rather than inputting sub-answers step by step. In this case the calculator steps will be:

Example 2.3

A cell phone is advertised for [latex]\scriptsize \text{R}280[/latex] per month on hire purchase over a period of three years. If the compound interest rate charged is [latex]\scriptsize 33.9\%[/latex], calculate the original cash price of the phone. What would the buyer save by buying the phone for cash rather than on hire purchase?

Solution

[latex]\scriptsize \begin{align*}n&=3\text{ years}\\i&=33.9\%\\A&=280\times (3\times 12)=10\text{ }080\\P&=?\end{align*}[/latex]
[latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{3}}\\\displaystyle \frac{A}{{{{{(1+i)}}^{3}}}}&=P\\P&=\displaystyle \frac{{10\text{ }080}}{{{{{(1+0.339)}}^{3}}}}\\&=\displaystyle \frac{{10\text{ }080}}{{{{{(1.339)}}^{3}}}}\\&=\displaystyle \frac{{10\text{ }080}}{{2.4007}}\\&=4\text{ }198.738\end{align*}[/latex]
The cash price for the phone is [latex]\scriptsize \text{R}4\text{ 198}\text{.74}[/latex].
The buyer would save [latex]\scriptsize 10\text{ }080-4\text{ }198.74=R5\text{ }881.26[/latex] by paying cash rather than buying on hire purchase.

Note: If you compare this to Example 1.3 in unit 1, you will see that the compound interest on a phone costing [latex]\scriptsize \text{R}4\text{ 198}\text{.74}[/latex] is more than the simple interest at the same rate and over the same period on a phone costing [latex]\scriptsize \text{R}4\text{ 997}\text{.52}[/latex]. Compound interest thus accumulates faster than simple interest.

Exercise 2.1

1. [latex]\scriptsize \text{R}3\text{ }750[/latex] is invested in a savings account at [latex]\scriptsize 3.2\%[/latex] compound interest per annum.
   1. What is the total value of the investment after a period of four years?
   2. Explain how this answer compares to question 1 of Exercise 1.1 in unit 1, in which the given values are the same, but simple interest is calculated.
2. A laptop is advertised for [latex]\scriptsize \text{R}299[/latex] per month on hire purchase over a period of three years.
   1. If the compound interest rate charged is [latex]\scriptsize 35\%[/latex], calculate the original cash price of the laptop. How much would the buyer save by buying for cash rather than on hire purchase?
   2. Explain how this answer compares to question 3 of Exercise 1.1 in unit 1, in which the figures are the same, but simple interest is calculated.
3. Lusanda invests [latex]\scriptsize \text{R}10\text{ 000}[/latex], and after eight years her investment triples. Calculate the interest rate per annum if the interest was:
   1. simple interest
   2. compounded annually?
4. Thabiso needs to borrow [latex]\scriptsize \text{R}75\text{ 000}[/latex] to buy a machine for his business. The debt will be paid in six years’ time when one of his investments matures. There are two options:
   Option 1: Borrow the money from a relative at [latex]\scriptsize 18\text{ }\%[/latex] p.a. simple interest.
   Option 2: Borrow from a bank at an interest rate of [latex]\scriptsize 15\text{ }\% \text{ }[/latex] p.a. compound interest.
   .
   Indicate which is the cheaper option and calculate the amount of money that will be saved by choosing the cheaper option.

The full solutions are at the end of the unit.

Note

Compound interest is accumulated on the original amount saved/borrowed and on the interest already accumulated. Think of it like earning interest on interest. For example, the graph below shows the growth of [latex]\scriptsize \text{R}100[/latex] saved in each of two different accounts. The green line represents growth of [latex]\scriptsize 10\text{ }\%[/latex] simple interest over [latex]\scriptsize 40[/latex] years, while the purple line represents growth of [latex]\scriptsize 10\text{ }\%[/latex] compound interest over the same period.

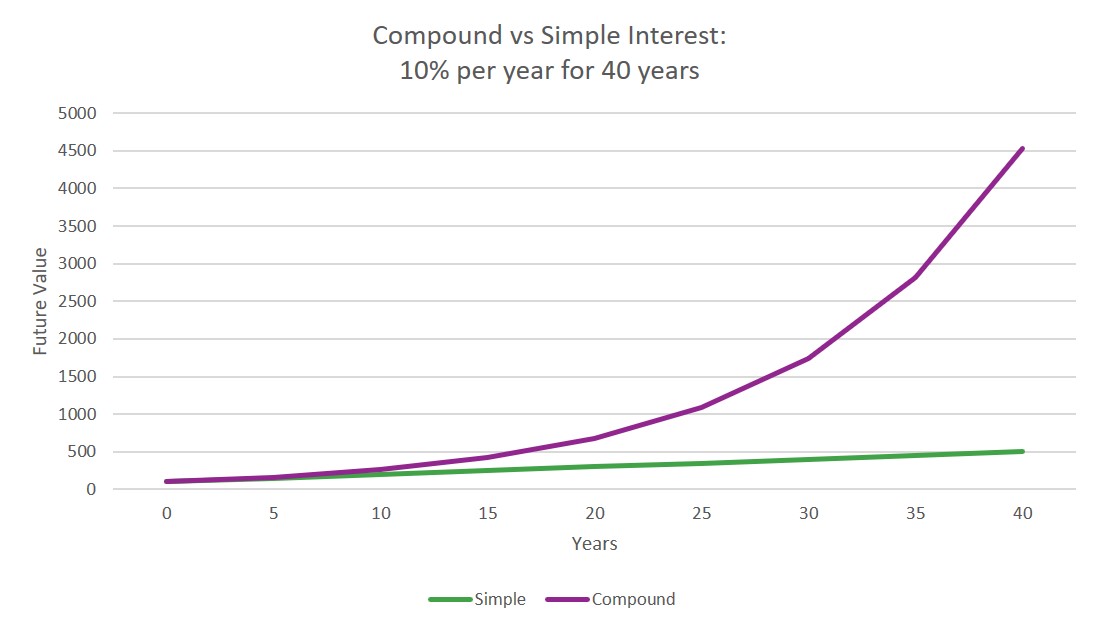
As you can see, compound interest grows your money much faster than simple interest, over the longer term.

Compounding interest more frequently than annually

The interest calculated on a principal amount can be added (or compounded) more often than annually, and this can be any regular period of time during the year. The most common are:

• semi-annually (i.e. every six months)
• quarterly (i.e. every three months)
• monthly
• daily.

The following slight changes to the compound interest formula allow these variations in the frequency of compounding to be taken into account:

• Dividing the interest rate by [latex]\scriptsize m[/latex] (the number of times it is compounded per unit time) results in the total amount of interest added per unit time being split into [latex]\scriptsize m[/latex] equal portions.
• Multiplying the index [latex]\scriptsize t[/latex] by [latex]\scriptsize m[/latex] results in the total number of additions of interest being [latex]\scriptsize m[/latex] every time period for [latex]\scriptsize t[/latex] time periods, i.e. [latex]\scriptsize t\times m[/latex].
• In the formula [latex]\scriptsize A=P{{(1+i)}^{n}}[/latex], [latex]\scriptsize i[/latex] represents the interest rate expressed as a percentage. If we were doing a calculation based on [latex]\scriptsize 12\text{ }\% \text{ }[/latex] interest, we would substitute [latex]\scriptsize i=\displaystyle \frac{{12}}{{100}}=0.12[/latex]. However, in the formula above, the conversion to a percentage (dividing by [latex]\scriptsize 100[/latex]) is included in the formula. Doing a calculation based on [latex]\scriptsize 12\text{ }\% \text{ }[/latex] interest using this formula, we would substitute [latex]\scriptsize r=12[/latex], seeing that the division by 100 is built into the formula.

Take note!

If the compounding period is not specifically mentioned, it should be assumed that compounding of interest takes place annually.

Example 2.4

[latex]\scriptsize \text{R}25\text{ }000[/latex] is deposited into a savings account. Calculate the value of the investment at the end of eight years, if the interest rate is:

1. [latex]\scriptsize 12\text{ }\%[/latex] p.a. compounded annually
2. [latex]\scriptsize 12\text{ }\%[/latex] p.a. compounded semi-annually
3. [latex]\scriptsize 12\text{ }\%[/latex] p.a. compounded quarterly
4. [latex]\scriptsize 12\text{ }\%[/latex] p.a. compounded monthly
5. [latex]\scriptsize 12\text{ }\%[/latex] p.a. compounded daily.

Solution

[latex]\scriptsize P=25\text{ }000;\text{ }t=8\text{; }r=12[/latex]

1. Annual compounding: [latex]\scriptsize m=1[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\&=25\text{ }000{{\left( {1+\displaystyle \frac{{12}}{{100\times 1}}} \right)}^{{8\times 1}}}\\&=25\text{ }000{{(1+0.12)}^{8}}\\&=25\text{ }000{{(1.12)}^{8}}\\&=25\text{ }000(2.47596)\\&=\text{R}61\text{ 899}\text{.08}\end{align*}[/latex]
   .
   Note: Remember that it is important to avoid round-off errors, so you need to think about how you will use your calculator so that you round off only at the final answer. BODMAS is a good guide to operations that should take priority, starting with Brackets, and Of (here – powers Of), as follows:
   .
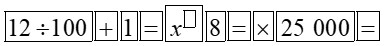   It is a good exercise to do the simpler calculations mentally, although you can always check your work with the calculator.
2. Semi-annual compounding: [latex]\scriptsize m=2[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\&=25\text{ }000{{\left( {1+\displaystyle \frac{{12}}{{100\times 2}}} \right)}^{{8\times 2}}}\\&=25\text{ }000{{(1+0.06)}^{{16}}}\\&=25\text{ }000{{(1.06)}^{{16}}}\\&=25\text{ }000(2.54035)\\&=\text{R}63\text{ 508}\text{.79}\end{align*}[/latex]
3. Quarterly compounding: [latex]\scriptsize m=4[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\&=25\text{ }000{{\left( {1+\displaystyle \frac{{12}}{{100\times 4}}} \right)}^{{8\times 4}}}\\&=25\text{ }000{{(1+0.03)}^{{32}}}\\&=25\text{ }000{{(1.03)}^{{32}}}\\&=25\text{ }000(2.575083...)\\&=\text{R}64\text{ 377}\text{.07}\end{align*}[/latex]
4. Monthly compounding: [latex]\scriptsize m=12[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\&=25\text{ }000{{\left( {1+\displaystyle \frac{{12}}{{100\times 12}}} \right)}^{{8\times 12}}}\\&=25\text{ }000{{(1+0.01)}^{{96}}}\\&=25\text{ }000{{(1.01)}^{{96}}}\\&=25\text{ }000(2.599272..)\\&=\text{R}64\text{ 981}\text{.82}\end{align*}[/latex]
5. Daily compounding: [latex]\scriptsize m=365[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\&=25\text{ }000{{\left( {1+\displaystyle \frac{{12}}{{100\times 365}}} \right)}^{{8\times 365}}}\\&=25\text{ }000{{(1+0.000328767...)}^{{2\text{ }920}}}\\&=25\text{ }000{{(1.000328767...)}^{{2\text{ }920}}}\\&=25\text{ }000(2.611284..)\\&=\text{R}65\text{ 282}\text{.11}\end{align*}[/latex]

Example 2.5

[latex]\scriptsize \displaystyle \text{R}120\text{ 000}[/latex] was deposited into a fixed deposit savings account for five years. The accumulated amount in the account at the end of the five-year period is [latex]\scriptsize \text{R}195\text{ 000}[/latex]. Calculate correct to one decimal place the interest rate per annum paid by the bank if:

1. the interest was compounded semi-annually
2. the interest was compounded daily.

Solution

1. [latex]\scriptsize A=195\text{ }000;\text{ P}=120\text{ }000;\text{ }t=5\text{; }m=2[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\\displaystyle \frac{A}{P}&={{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\\sqrt[{t\times m}]{{\displaystyle \frac{A}{P}}}&=1+\displaystyle \frac{r}{{100\times m}}\\\displaystyle \frac{r}{{100\times m}}&=\sqrt[{t\times m}]{{\displaystyle \frac{A}{P}}}-1\\r&=100m\left( {\sqrt[{t\times m}]{{\displaystyle \frac{A}{P}}}-1} \right)\\r&=200\left( {\sqrt[{10}]{{\displaystyle \frac{{195\text{ }000}}{{120\text{ }000}}}}-1} \right)\\&=200\left( {\sqrt[{10}]{{1.625}}-1} \right)\\&=200\left( {0.0497...} \right)\\&=9.5\text{ }\% \text{ }\end{align*}[/latex]
2. [latex]\scriptsize A=195000;\text{ P}=120000;\text{ }t=5\text{; }m=365[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\\displaystyle \frac{A}{P}&={{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\\sqrt[{t\times m}]{{\displaystyle \frac{A}{P}}}&=1+\displaystyle \frac{r}{{100\times m}}\\\displaystyle \frac{r}{{100\times m}}&=\sqrt[{t\times m}]{{\displaystyle \frac{A}{P}}}-1\\r&=36\ 500\left( {\sqrt[{t\times m}]{{\displaystyle \frac{A}{P}}}-1} \right)\\r&=36\ 500\left( {\sqrt[{5\times 365}]{{\displaystyle \frac{{195\text{ }000}}{{120\text{ }000}}}}-1} \right)\\&=36\ 500\left( {\sqrt[{1\text{ 825}}]{{1.625}}-1} \right)\\&=36\ 500\left( {0.000266...} \right)\\&=9.7\text{ }\% \text{ }\end{align*}[/latex]

Example 2.6

Find the amount of money that must be invested for five years at [latex]\scriptsize 3\text{ }\%[/latex] per annum, compounded monthly, to accumulate to [latex]\scriptsize \text{R}35\text{ 000}[/latex] by the end of the period.

Solution

[latex]\scriptsize A=35\ 000\text{; }t=5;\text{ }r=3\%;\quad m=12[/latex]
[latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\P&=\displaystyle \frac{A}{{{{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}}^{{t\times m}}}}}\\&=\displaystyle \frac{{35\text{ }000}}{{{{{\left( {1+\displaystyle \frac{3}{{100\times 12}}} \right)}}^{{5\times 12}}}}}\\&=\displaystyle \frac{{35\text{ }000}}{{{{{\left( {1+\displaystyle \frac{3}{{1200}}} \right)}}^{{60}}}}}\\&=\displaystyle \frac{{35\text{ }000}}{{{{{(1+0.0025)}}^{{60}}}}}\\&=\displaystyle \frac{{35\text{ }000}}{{{{{(1.0025)}}^{{60}}}}}\\&=\displaystyle \frac{{35\text{ }000}}{{1.6162}}\\&=\text{R}30\text{ }130.42\end{align*}[/latex]

The power of compound interest lies in the length of time that an investment is allowed to grow. Our patience is the deciding factor.

Example 2.7

Suppose Kekeletso and Tshiamo start working at age [latex]\scriptsize 24[/latex]. Kekeletso works until she is [latex]\scriptsize 65[/latex] years old, and Tshiamo until he is [latex]\scriptsize 55[/latex] years old. At the end of their first year of work, they each invest [latex]\scriptsize \text{R}1\text{ }500[/latex] in a savings plan that offers [latex]\scriptsize 11.11\text{ }\%[/latex] interest compounded monthly. What difference will the extra [latex]\scriptsize 10[/latex] years make to the value of their investments?

Solution

The initial investment amounts and interest rates are the same for both investments. Only the time periods differ.

[latex]\scriptsize A=1\text{ }500\text{; }r=11.11\text{ }\%;\text{ }m=12[/latex]
For Kekeletso, [latex]\scriptsize t=65-25=40[/latex] years
[latex]\scriptsize \begin{align*}{{A}_{K}}&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\&=1\text{ }500{{\left( {1+\displaystyle \frac{{11.11}}{{100\times 12}}} \right)}^{{40\times 12}}}\\&=1\text{ }500{{\left( {1+\displaystyle \frac{{11.11}}{{1\text{ }200}}} \right)}^{{480}}}\\&=1\text{ }500{{\left( {1+0.009258} \right)}^{{480}}}\\&=1\text{ }500{{(1.009258)}^{{480}}}\\&=1\text{ }500(83.392)\\&=\text{R}125\text{ }088.21\end{align*}[/latex]
So, after a period of [latex]\scriptsize 40[/latex] years, Kekeletso’s investment of [latex]\scriptsize \text{R}1\text{ }500[/latex] would have grown to the amount of [latex]\scriptsize \text{R}125\text{ 088}\text{.21}[/latex].

On the other hand, Tshiamo’s investment had [latex]\scriptsize t=55-25=30[/latex] years to grow.
[latex]\scriptsize \begin{align*}{{A}_{T}}&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\&=1\text{ }500{{\left( {1+\displaystyle \frac{{11.11}}{{100\times 12}}} \right)}^{{30\times 12}}}\\&=1\text{ }500{{\left( {1+\displaystyle \frac{{11.11}}{{1\text{ }200}}} \right)}^{{360}}}\\&=1\text{ }500{{\left( {1+0.009258} \right)}^{{360}}}\\&=1\text{ }500{{(1.009258)}^{{360}}}\\&=1\text{ }500(27.59585)\\&=\text{R}41\text{ }393.78\end{align*}[/latex]
Although Tshiamo’s [latex]\scriptsize \text{R}1\text{ }500[/latex] investment had grown impressively to [latex]\scriptsize \text{R}41\text{ }393.78[/latex], Kekeletso’s investment was worth [latex]\scriptsize \text{R}125\text{ }088.21-\text{R}41\text{ }393.78=\text{R}83\text{ 694}\text{.43}[/latex] more, as a result of the additional [latex]\scriptsize 10[/latex] years. In total Kekeletso’s investment was worth just over three times as much as Tshiamo’s!

Exercise 2.2

1. [latex]\scriptsize \text{R}120\text{ 000}[/latex] is needed to start a business. A loan can be obtained from the small business development fund or from a bank. The loan must be repaid in one amount at the end of three years. The small business development fund charges [latex]\scriptsize 9\text{ }\%[/latex] p.a. simple interest. The bank charges [latex]\scriptsize 7.2\text{ }\% \text{ }[/latex] p.a. compounded monthly. Which loan is cheaper, and how much cheaper is it?
2. [latex]\scriptsize \text{R}750\text{ 000}[/latex] is deposited into a fixed deposit savings account for six years, and amounts to [latex]\scriptsize \text{R}1\text{ 094 505}\text{.70}[/latex] by the end of this period. Calculate the interest rate per annum paid by the bank if:
   1. the interest is compounded annually
   2. the interest is compounded daily.
3. Calculate the amount of money that must be invested at [latex]\scriptsize 11\text{ }\% \text{ }[/latex] p.a. compounded monthly, if the accumulated investment is [latex]\scriptsize \text{R}135\text{ 000}[/latex] after a period of [latex]\scriptsize 15[/latex] years.

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to use the compound growth formula (or compound interest formula) to solve problems related to finance.
• How to solve for [latex]\scriptsize A\text{, }P[/latex] and [latex]\scriptsize i[/latex] using the compound interest formula.
• How to compare simple interest growth to compound interest growth.
• How to solve compound growth problems with interest compounded at various different regular intervals (semi-annually, quarterly, monthly and daily).

Unit 2: Assessment

Suggested time to complete: 40 minutes

1. A shop offers a [latex]\scriptsize \text{R}5\text{ }299.00[/latex] laptop that can be paid off in three ways:
   1. over [latex]\scriptsize 12[/latex] months at [latex]\scriptsize \text{R}627.67[/latex] per month
   2. over [latex]\scriptsize 24[/latex] months at [latex]\scriptsize \text{R}382.88[/latex] per month
   3. over [latex]\scriptsize 36[/latex] months at [latex]\scriptsize \text{R}303.70[/latex] per month.

Calculate the total amount paid for each option, and the compound interest rate charged for each.

2. [latex]\scriptsize \text{R}2\text{ }500[/latex] is deposited in each of the following:
   Option A: a savings account that pays [latex]\scriptsize 3.25\text{ }\%[/latex] compound interest, and permits immediate access to its funds
   Option B: a savings account paying [latex]\scriptsize 4.35\text{ }\% \text{ }[/latex] compound interest, where withdrawals require [latex]\scriptsize 32[/latex] days’ advance notice, or a penalty to be paid.
   If no withdrawals are made from either account, what will their balances be after three years?
3. What amount of money should be invested at [latex]\scriptsize 4\text{ }\%[/latex] p.a. compound interest to amount to [latex]\scriptsize \text{R}350\text{ 000}[/latex] in [latex]\scriptsize 20[/latex] years’ time?
4. [latex]\scriptsize \text{R}5\text{ 700}[/latex] was invested in a savings account at [latex]\scriptsize 8.75\text{ }\%[/latex] p.a. Calculate how much more money is in the account at the end of [latex]\scriptsize 18[/latex] months if interest is compounded daily than if interest is compounded semi-annually.

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. .
   1. [latex]\scriptsize P=\text{R}3\text{ 750}[/latex]
      [latex]\scriptsize i=3.2\text{ }\%[/latex]
      [latex]\scriptsize n=4[/latex]
      [latex]\scriptsize A=?[/latex]
      .
      [latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{n}}\\&=3\text{ }750{{\left( {1+\displaystyle \frac{{3.2}}{{100}}} \right)}^{4}}\\&=3\text{ }750{{(1+0.032)}^{4}}\\&=3\text{ }750{{(1.032)}^{4}}\\&=3\text{ }750(1.134)\\&=4\text{ }253.54\end{align*}[/latex]
      The total value of the investment after the period of four years is [latex]\scriptsize \text{R}4\text{ 230}[/latex].
   2. This is [latex]\scriptsize \text{R}23.54[/latex] more than if simple interest at the same rate had been calculated over the same period.
2. .
   1. [latex]\scriptsize n=3\text{ years}=36\text{ months}[/latex]
      [latex]\scriptsize i=35\text{ }\%[/latex]
      [latex]\scriptsize A=299\times 36=10\text{ }764[/latex]
      .
      [latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{n}}\\\displaystyle \frac{A}{{{{{(1+i)}}^{n}}}}&=P\\P&=\displaystyle \frac{{10\text{ }764}}{{{{{\left( {1+\displaystyle \frac{{35}}{{100}}} \right)}}^{3}}}}\\&=\displaystyle \frac{{10\text{ }764}}{{{{{(1+0.35)}}^{3}}}}\\&=\displaystyle \frac{{10\text{ }764}}{{{{{1.35}}^{3}}}}\&=\displaystyle \frac{{10\text{ }764}}{{2.460}}\\&=4\text{ }374.943\end{align*}[/latex]
      The original cash price of the laptop is [latex]\scriptsize \text{R}4\text{ }374.94[/latex].
      Buying for cash rather than on hire purchase would save [latex]\scriptsize \text{R}10\text{ }764-\text{R}4\text{ }374.94=\text{R}5\text{ }504.27[/latex]
   2. Comparing this to question 3 of Exercise 1.1 in unit 1, you can see that at the same rate and over the same period, the compound interest is greater.
3. .
   1. [latex]\scriptsize P=10\text{ 000}[/latex]
      [latex]\scriptsize A=3\times 10\text{ 000}=30\text{ 000}[/latex]
      [latex]\scriptsize n=8[/latex]
      [latex]\scriptsize \begin{align*}A&=P(1+i.n)\\\displaystyle \frac{A}{P}&=1+i.n\\\displaystyle \frac{A}{P}-1&=i.n\\\displaystyle \frac{1}{n}\left( {\displaystyle \frac{A}{P}-1} \right)&=i\\i&=\displaystyle \frac{1}{8}\left( {\displaystyle \frac{{30\text{ }000}}{{10\text{ }000}}-1} \right)\\&=\displaystyle \frac{1}{8}(3-1)\\&=\displaystyle \frac{1}{8}(2)\\&=0.25\text{ }\%\text{ simple interest}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{n}}\\\displaystyle \frac{A}{P}&={{(1+i)}^{n}}\\\sqrt[8]{{\displaystyle \frac{A}{P}}}&=1+i\\i&=\sqrt[8]{{\displaystyle \frac{A}{P}}}-1\\&=\sqrt[8]{{\displaystyle \frac{{30\text{ }000}}{{10\text{ }000}}}}-1\\&=\sqrt[8]{3}-1\\&=1.147-1\\&=0.147\text{ }\%\end{align*}[/latex]
      Note: A lower rate of compound interest achieves the same amount of growth as a higher rate of simple interest.
4. [latex]\scriptsize P=75\text{ }000[/latex]
   [latex]\scriptsize n=6\text{ years}[/latex]
   [latex]\scriptsize A=?[/latex]
   Option A: [latex]\scriptsize i=18\text{ }\%\text{ p}\text{.a}\text{. simple interest}[/latex]
   [latex]\scriptsize \begin{align*}A&=P(1+i.n)\\&=75\text{ }000[1+(0.18)(6)]\\&=75\text{ }000[1+1.08]\\&=75\text{ }000(2.08)\\&=\text{R}156\text{ 000}\end{align*}[/latex]
   .
   Option B: [latex]\scriptsize i=15\text{ }\%\text{ compound interest}[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{n}}\\&=75\text{ }000{{(1+0.15)}^{6}}\\&=75\text{ }000{{(1.15)}^{6}}\\&=75\text{ }000(2.3131)\\&=\text{R}173\text{ 479}\text{.56}\end{align*}[/latex]
   Borrowing at [latex]\scriptsize 18\text{ }\%[/latex] simple interest is cheaper than [latex]\scriptsize 15\text{ }\%[/latex] compound interest. By doing this, there will be a saving of [latex]\scriptsize \text{R}173\text{ 479}\text{.56}-\text{R}156\text{ 000=R17 479}\text{.56}[/latex].

Back to Exercise 2.1

Exercise 2.2

1. [latex]\scriptsize P=\text{R}120\text{ }000[/latex]
   [latex]\scriptsize n=3\text{ years}[/latex]
   Small business development fund: [latex]\scriptsize i=9\text{ }\%=0.09\text{ p}\text{.a}\text{. simple interest}[/latex]
   [latex]\scriptsize \begin{align*}A&=120\text{ }000(1+0.09\times 3)\\&=120\text{ }000(1.27)\\&=\text{R}152\text{ 000}\end{align*}[/latex]
   .
   Bank: [latex]\scriptsize i=7.2\text{ }\%\text{ p}\text{.a}\text{. compounded monthly}[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{{7.2}}{{100\times 12}}} \right)}^{{3\times 12}}}\\&=120\text{ }000{{\left( {1+\displaystyle \frac{{7.2}}{{1200}}} \right)}^{{36}}}\\&=120\text{ }000{{(1.006)}^{{36}}}\\&=120\text{ }000(1.240)\\&=\text{R}148\text{ 836}\text{.19}\end{align*}[/latex]
   .
   The bank loan at [latex]\scriptsize 7.2\text{ }\% \text{ }[/latex] p.a. compounded monthly is cheaper:
   [latex]\scriptsize \text{R}152\text{ }000-\text{R}148\text{ }836.19=\text{R}3\text{ 163}\text{.81}[/latex]
2. .
   1. If the interest is compounded annually:
      [latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{n}}\\\sqrt[n]{{\displaystyle \frac{A}{P}}}&=1+i\\i&=\sqrt[n]{{\displaystyle \frac{A}{P}}}-1\\&=\sqrt[6]{{\displaystyle \frac{{1\text{ }094\text{ }505.70}}{{750\text{ }000}}}}-1\\&=1.065-1\\&=6.5\text{ }\% \text{ }\end{align*}[/latex]
   2. If the interest is compounded daily:
      [latex]\scriptsize \begin{align*}A&=P{{(1+\displaystyle \frac{r}{{100\times m}})}^{{t\times m}}}\\\displaystyle \frac{A}{P}&={{(1+\displaystyle \frac{r}{{100\times 365}})}^{{6\times 365}}}\\\sqrt[{2190}]{{\displaystyle \frac{{1094505.70}}{{750000}}}}&=1+\displaystyle \frac{r}{{36\ 500}}\\\displaystyle \frac{r}{{36500}}&=\sqrt[{2190}]{{\displaystyle \frac{{1094505.70}}{{750000}}}}-1\\r&=36500\left( {\sqrt[{2190}]{{\displaystyle \frac{{1094505.70}}{{750000}}}}-1} \right)\text{ }\\r&=36500(1.0001726-1)\text{ }\\r&=6.3\text{ }\%\end{align*}[/latex]
3. [latex]\scriptsize A=\text{R}135\text{ }000\text{ }i=11\text{ }\% \text{ p}\text{.a}\text{. compounded monthly }t=15\text{ years}[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}^{{t\times m}}}\\\displaystyle \frac{A}{{{{{\left( {1+\displaystyle \frac{r}{{100\times m}}} \right)}}^{{t\times m}}}}}&=P\\P&=\displaystyle \frac{{135\text{ }000}}{{{{{\left( {1+\displaystyle \frac{{11}}{{100\times 12}}} \right)}}^{{15\times 12}}}}}\\&=\displaystyle \frac{{135\text{ }000}}{{{{{\left( {1.00917} \right)}}^{{180}}}}}\\&=\displaystyle \frac{{135\text{ }000}}{{5.168}}\\&=\text{R}26\text{ }122.35\end{align*}[/latex]
   [latex]\scriptsize \text{R}26\text{ 122}\text{.35}[/latex] would need to be invested.

Back to Exercise 2.2

Unit 2: Assessment

1. [latex]\scriptsize P=5\text{ }299[/latex]
   1. [latex]\scriptsize A=12\times 627.67=7\text{ }532.04[/latex]; this is the cost of the laptop in this option
      [latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{n}}\\\displaystyle \frac{A}{P}&={{(1+i)}^{n}}\\{{(1+i)}^{1}}&=\displaystyle \frac{A}{P}\\1+i&=\displaystyle \frac{{7\text{ }532.04}}{{5\text{ }299}}\\i&=1.4214-1\\i&=0.4214\%\text{ p}\text{.a}\text{.}\end{align*}[/latex]
      Note: With the period being one year, the simple interest formula and compound interest formula produce the same answer.
   2. [latex]\scriptsize A=24\times \text{R}382.88=\text{R}9\text{ }189.12[/latex]; this is the cost of the laptop in this option
      [latex]\scriptsize \begin{align*}{{(1+i)}^{2}}&=\displaystyle \frac{A}{P}\\1+i&=\sqrt{{\displaystyle \frac{A}{P}}}\\i&=\sqrt{{\displaystyle \frac{{9189.12}}{{5299}}}}-1\\&=\sqrt{{1.7341}}-1\\&=1.3169-1\\&=0.3169\%\text{ p}\text{.a}\text{.}\end{align*}[/latex]
   3. [latex]\scriptsize A=36\times \text{R}303.70=\text{R}10\text{ }933.20[/latex]; this is the cost of the laptop in this option
      [latex]\scriptsize \begin{align*}{{(1+i)}^{3}}&=\displaystyle \frac{A}{P}\\1+i&=\sqrt[3]{{\displaystyle \frac{{10\text{ }933.2}}{{5\text{ }299}}}}\\i&=\sqrt[3]{{2.06326}}-1\\&=1.2731-1\\&=0.2731\%\text{ p}\text{.a}\text{.}\end{align*}[/latex]
2. [latex]\scriptsize P=2\text{ }500[/latex]
   Option A: [latex]\scriptsize i=3.25\text{ }\%[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{n}}\\&=2\text{ }500{{(1+0.0325)}^{3}}\\&=2\text{ }500{{(1.0325)}^{3}}\\&=2\text{ }500(1.1007)\\&=\text{R}2\text{ }751.76\end{align*}[/latex]
   .
   Option B: [latex]\scriptsize i=4.35\text{ }\%[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{n}}\\&=2\text{ }500{{(1+0.0435)}^{3}}\\&=2\text{ }500{{(1.0435)}^{3}}\\&=2\text{ }500(1.1353)\\&=\text{R}2\text{ }840.65\end{align*}[/latex]
3. [latex]\scriptsize A=350\text{ }000;\text{ }n=20;\text{ }i=4\text{ }\%\text{ }p.a.[/latex]
   [latex]\scriptsize \begin{align*}A&=P{{(1+i)}^{n}}\\\displaystyle \frac{A}{{{{{(1+i)}}^{n}}}}&=P\\P&=\displaystyle \frac{{350\text{ }000}}{{{{{(1+0.04)}}^{{20}}}}}\\&=\displaystyle \frac{{350\text{ }000}}{{{{{(1.04)}}^{{20}}}}}\\&=\displaystyle \frac{{350\text{ }000}}{{2.1912}}\\&=\text{R}159\text{ }735.43\end{align*}[/latex]

Back to Unit 2: Assessment