Unit outcomes

By the end of this unit you will be able to:

• Solve real problems by applying the area, sine and cosine rules.

What you should know

• Before you start this unit, make sure you can:
• Use the area rule. Refer to unit 5 of this subject outcome if you need help with this.
• Use the sine rule to find unknown sides and angles of triangles. Refer to unit 6 of this subject outcome if you need help with this.
• Use the cosine rule to find unknown sides and angles of triangles. Refer to unit 7 of this subject outcome if you need help with this.

Introduction

This is the final unit in this subject outcome. In this unit, we are going to bring much of what we have already learnt together to solve some problems in two dimensions. We will particularly be using the area, sine and cosine rules to work out unknown areas, sides and angles of triangles. Read the following note carefully about how to determine which of these rules to use, and when.

Take note!

Use the area rule if:

• no perpendicular height is given.

Use the sine rule if:

• no right angle is given
• two sides and an angle are given (not the included angle)
• two angles and a side are given.

Use the cosine rule if:

• no right angle is given
• two sides and the included angle are given
• three sides are given.

Bearings and angles of elevation and depression

Before we get into solving 2-D problems, it is important that you understand what is meant by a bearing, and by angles of elevation and depression.

We can measure direction using bearings. Bearings are measured as the angle from the north rotated in a clockwise direction. For example, Figure 1 shows a point [latex]\scriptsize \text{A}[/latex] at a bearing of [latex]\scriptsize {{215}^\circ}[/latex].

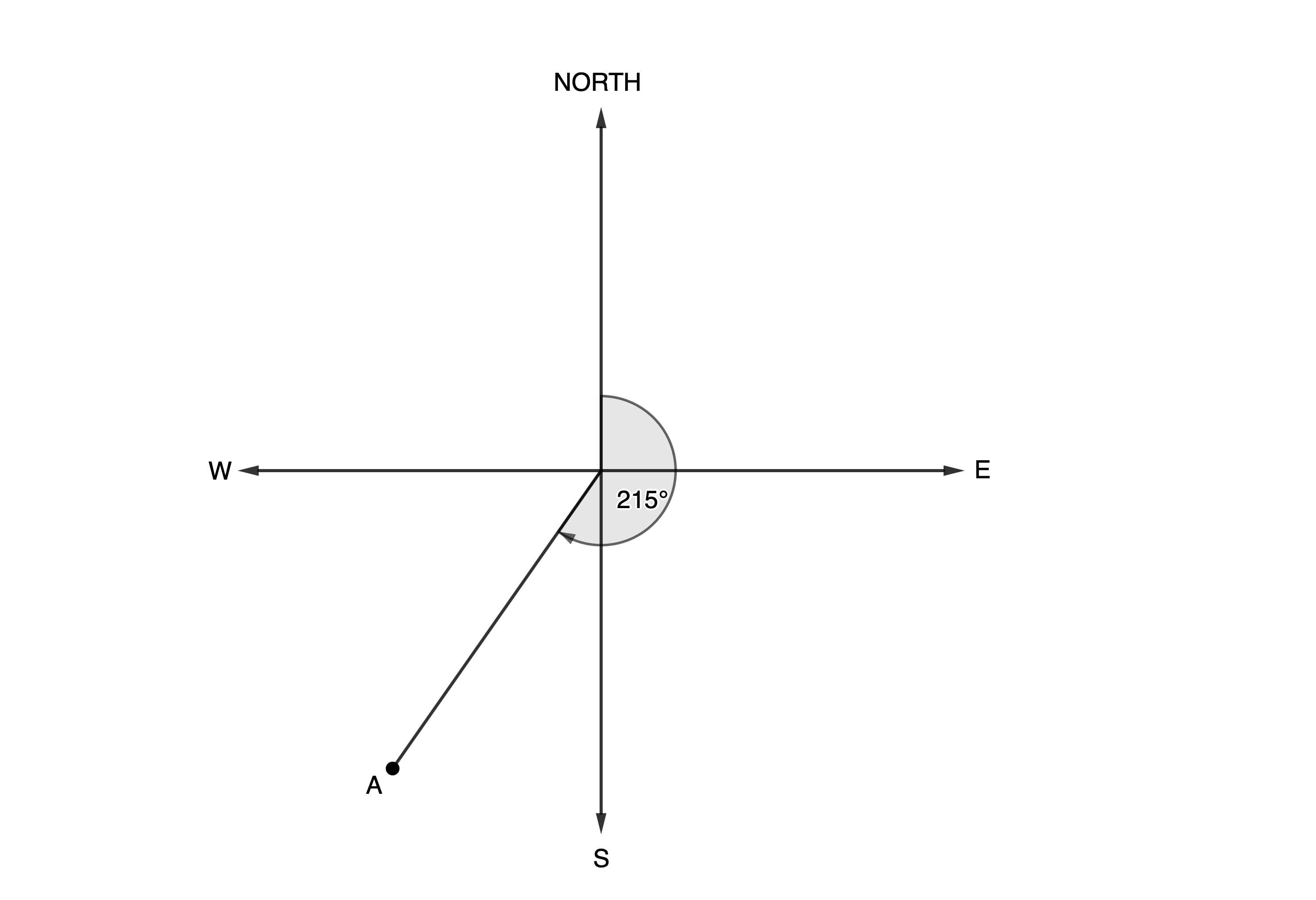
We can also measure direction as the number of degrees from any of the cardinal directions. For example, in Figure 2, point [latex]\scriptsize \text{A}[/latex] is [latex]\scriptsize \text{W}{{16}^\circ}\text{S}[/latex] or [latex]\scriptsize {{16}^\circ}[/latex] south of due west.

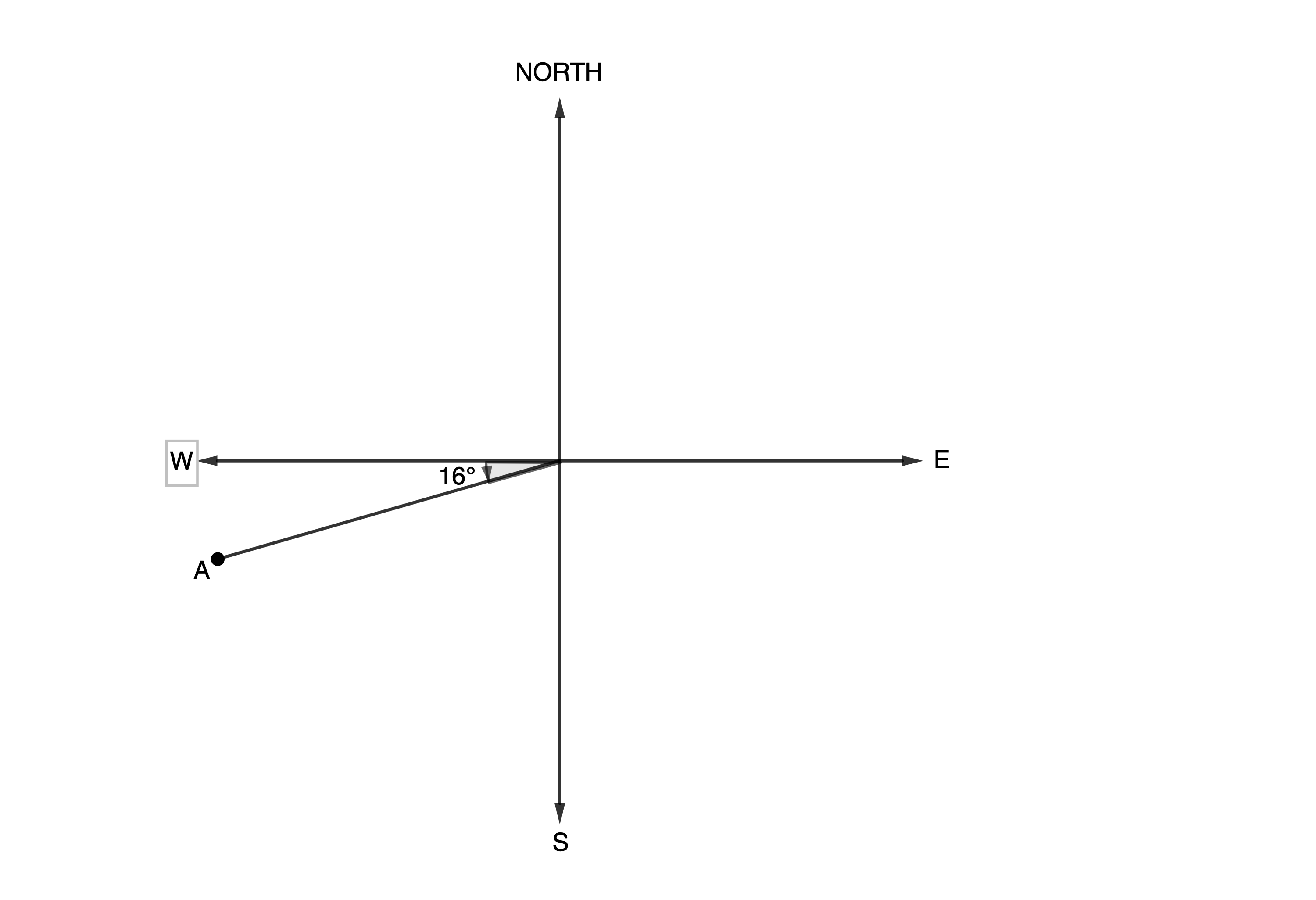
We measure how far an object is above a horizontal line using an angle of elevation. Figure 3 shows point [latex]\scriptsize \text{A}[/latex] at an angle of elevation of [latex]\scriptsize {{35}^\circ}[/latex].

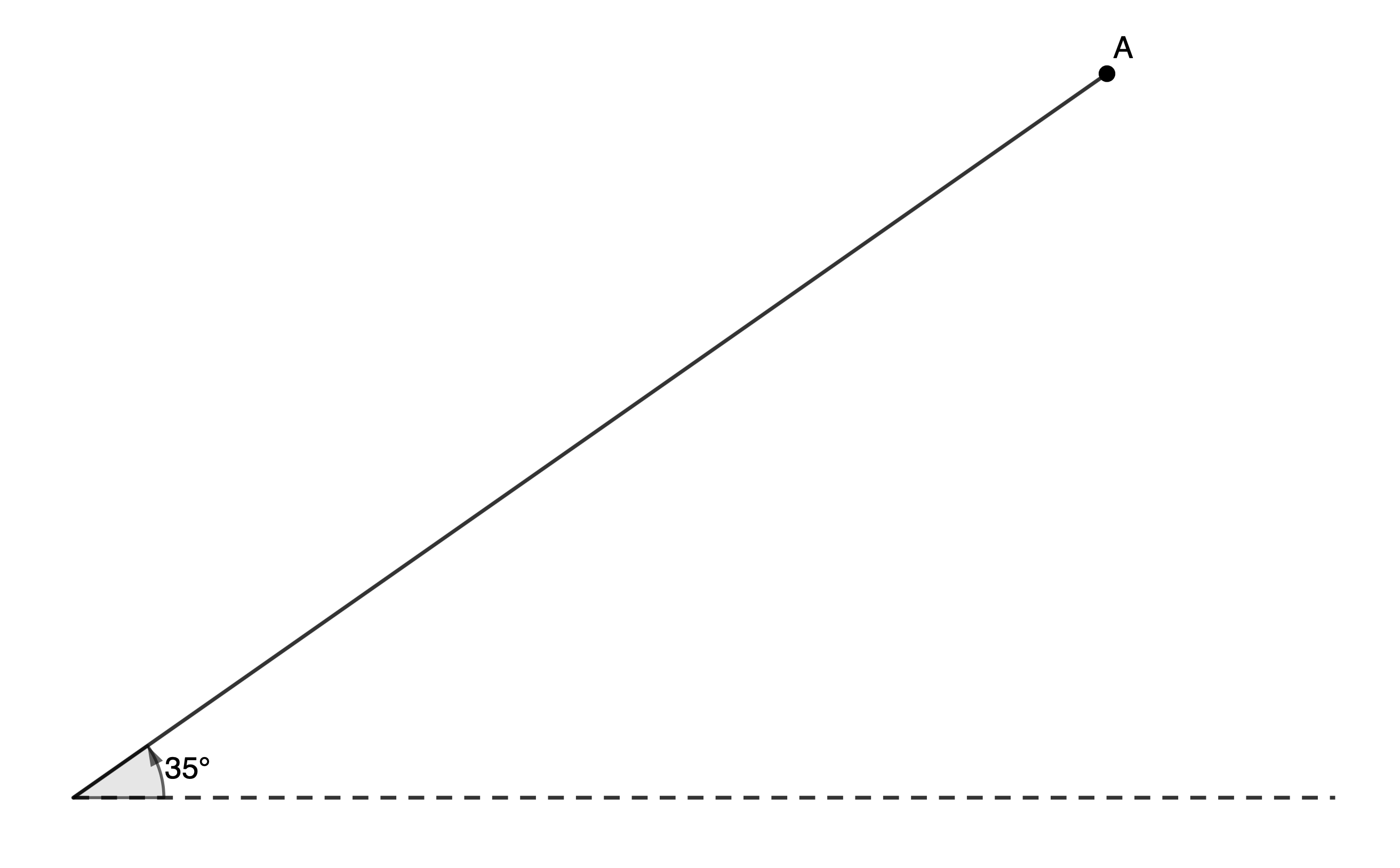
Similarly, we measure how far below the horizontal something is using an angle of depression. Figure 4 shows point [latex]\scriptsize \text{A}[/latex] at an angle of depression of [latex]\scriptsize {{47}^\circ}[/latex].

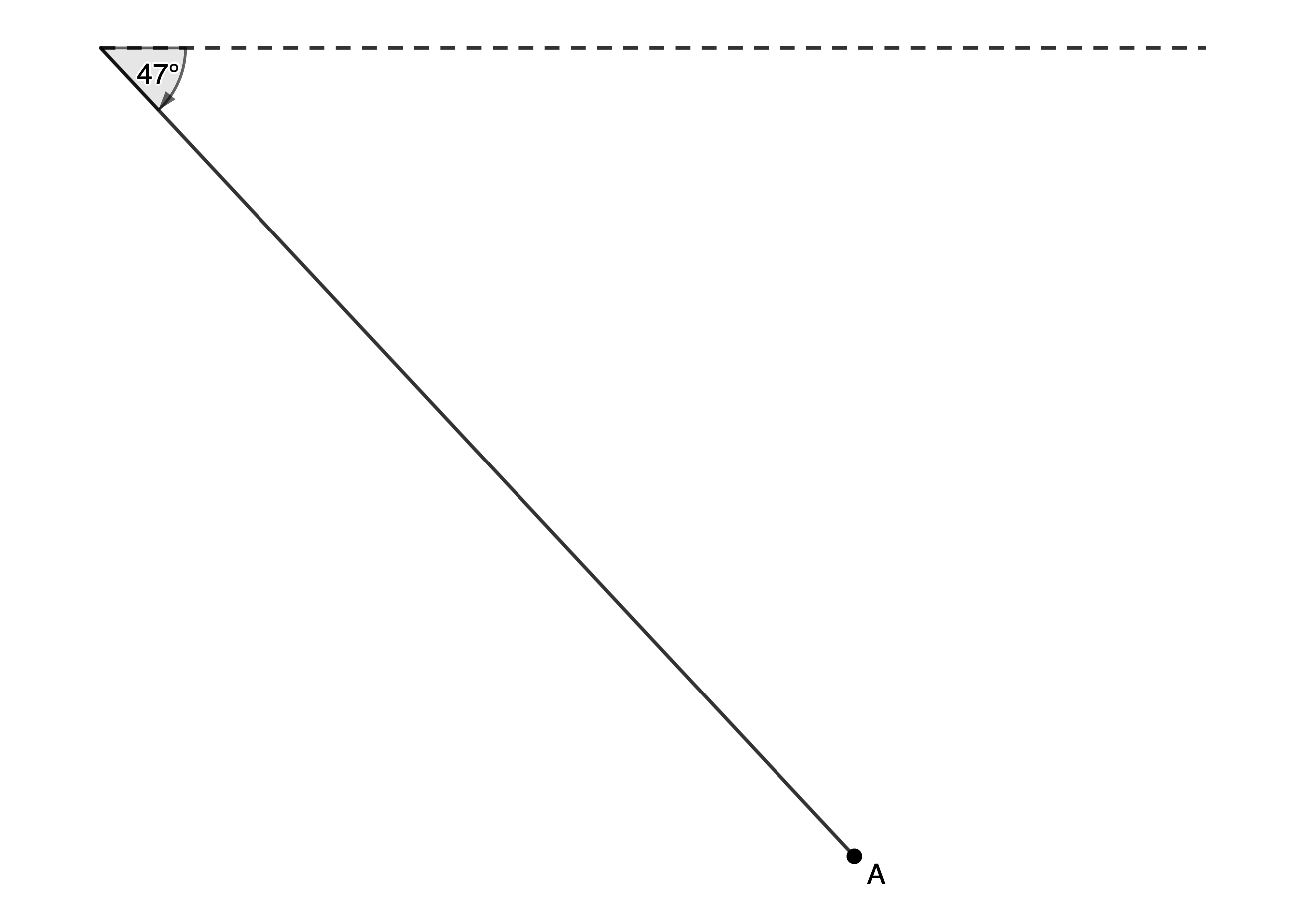
Solving problems in 2-D

Let’s now look at how we solve different types of two-dimensional problems.

Example 8.2

Two observers at [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex] respectively, are watching workmen fixing power lines at [latex]\scriptsize C[/latex]. The angle of elevation from [latex]\scriptsize A[/latex] to [latex]\scriptsize C[/latex] is [latex]\scriptsize {{37}^\circ}[/latex] and the angle of elevation from [latex]\scriptsize B[/latex] to [latex]\scriptsize C[/latex] is [latex]\scriptsize {{25}^\circ}[/latex]. If the observers are standing [latex]\scriptsize 15\ \text{m}[/latex] apart, calculate the height of the pole [latex]\scriptsize CD[/latex], correct to one decimal place.

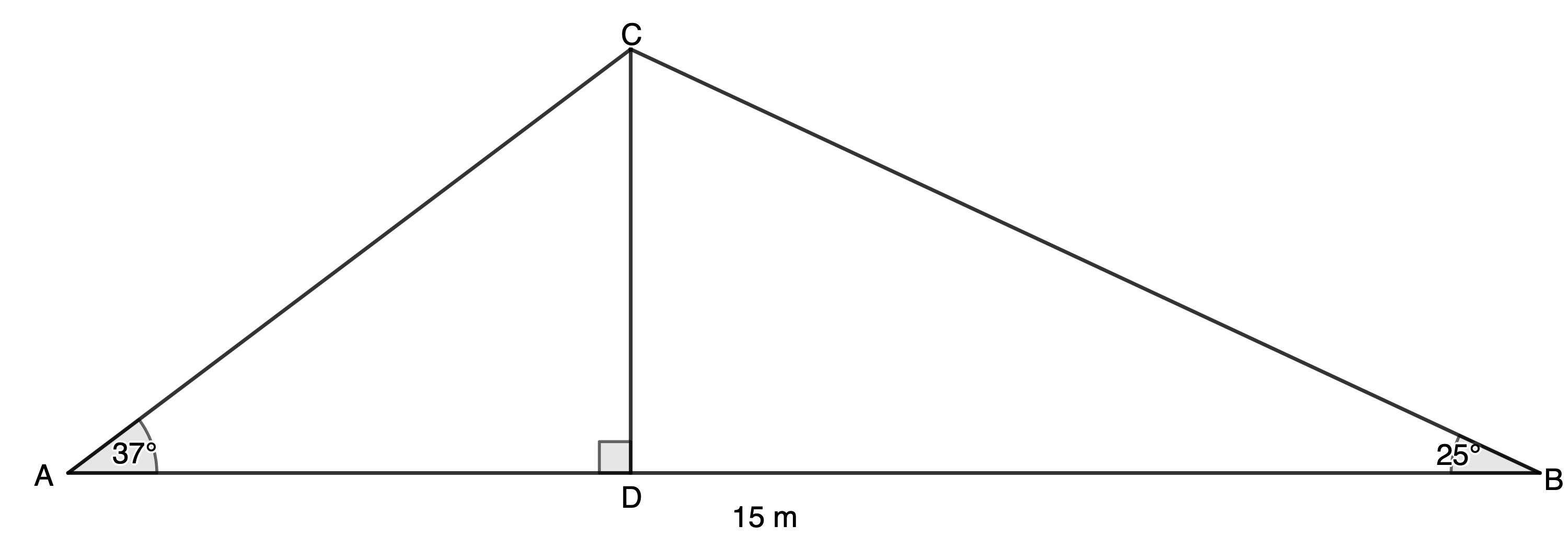
Solution

To calculate the length of [latex]\scriptsize CD[/latex], we first need to find the length of [latex]\scriptsize AC[/latex] or [latex]\scriptsize BC[/latex]. Then we can work in either of these smaller triangles to calculate [latex]\scriptsize CD[/latex]. To get [latex]\scriptsize AC[/latex] or [latex]\scriptsize BC[/latex] we need [latex]\scriptsize \hat{C}[/latex] which we can easily calculate.

[latex]\scriptsize \hat{C}={{180}^\circ}-\hat{A}-\hat{B}={{180}^\circ}-{{37}^\circ}-{{25}^\circ}={{118}^\circ}[/latex] (angles in a triangle are supplementary)
[latex]\scriptsize \begin{align*}\displaystyle \frac{{AC}}{{\sin B}} & =\displaystyle \frac{{AB}}{{\sin C}}\\\therefore \displaystyle \frac{{AC}}{{\sin {{{25}}^\circ}}} & =\displaystyle \frac{{15}}{{\sin {{{118}}^\circ}}}\\\therefore AC & =\displaystyle \frac{{15\sin {{{25}}^\circ}}}{{\sin {{{118}}^\circ}}}\\ & =7.18\ \text{m}\end{align*}[/latex]

Now that we have the length of [latex]\scriptsize AC[/latex] we can work in [latex]\scriptsize \Delta ACD[/latex] to determine [latex]\scriptsize CD[/latex].
[latex]\scriptsize \begin{align*}\displaystyle \frac{{CD}}{{\sin A}} & =\displaystyle \frac{{AC}}{{\sin C\hat{D}A}}\\\therefore \displaystyle \frac{{CD}}{{\sin {{{37}}^\circ}}} & =\displaystyle \frac{{7.18}}{{\sin {{{90}}^\circ}}}\\\therefore CD & =\displaystyle \frac{{7.18\sin {{{37}}^\circ}}}{{\sin {{{90}}^\circ}}}\\ & =4.32\ \text{m}\end{align*}[/latex]

Example 8.2

Two ships leave a harbour, [latex]\scriptsize H[/latex], at the same time. The first ship sails [latex]\scriptsize 42\ \text{km}[/latex] to point [latex]\scriptsize A[/latex] in a direction of [latex]\scriptsize \text{N}{{55}^\circ}\text{E}[/latex]. The second ship sails for [latex]\scriptsize 60\ \text{km}[/latex] to point [latex]\scriptsize B[/latex] on a bearing of [latex]\scriptsize {{315}^\circ}[/latex]. How far apart are the points [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex]?

Solution

We are not given a diagram of the situation so the first thing we need to do is to sketch our own. It does not need to be perfectly accurate or to scale. Always make sure you have a diagram representing the given information before trying to calculate anything.

We need to calculate the distance [latex]\scriptsize AB[/latex]. We will be working in [latex]\scriptsize \Delta ABH[/latex].
The angle between [latex]\scriptsize BH[/latex] and north is [latex]\scriptsize {{45}^\circ}[/latex] (angles around a point). Therefore, [latex]\scriptsize A\hat{H}B={{45}^\circ}+{{55}^\circ}={{100}^\circ}[/latex].

We can use the cosine rule to determine [latex]\scriptsize AB[/latex].
[latex]\scriptsize \begin{align*}A{{B}^{2}} & =A{{H}^{2}}+B{{H}^{2}}-2\cdot AH\cdot BH\cdot \cos A\hat{H}B\\\therefore A{{B}^{2}} & ={{42}^{2}}+{{60}^{2}}-2\cdot 42\cdot 60\cdot \cos {{100}^\circ}\\\therefore AB & =\sqrt{{{{{42}}^{2}}+{{{60}}^{2}}-2\cdot 42\cdot 60\cdot \cos {{{100}}^\circ}}}\\ & =78.99\ \text{km}\end{align*}[/latex]

NOTE: You might have noticed that the partial calculation for [latex]\scriptsize 2\cdot 42\cdot 60\cdot \cos {{100}^\circ}[/latex] gave a negative number. Remember that cosine is negative in the second quadrant.

Exercise 8.1

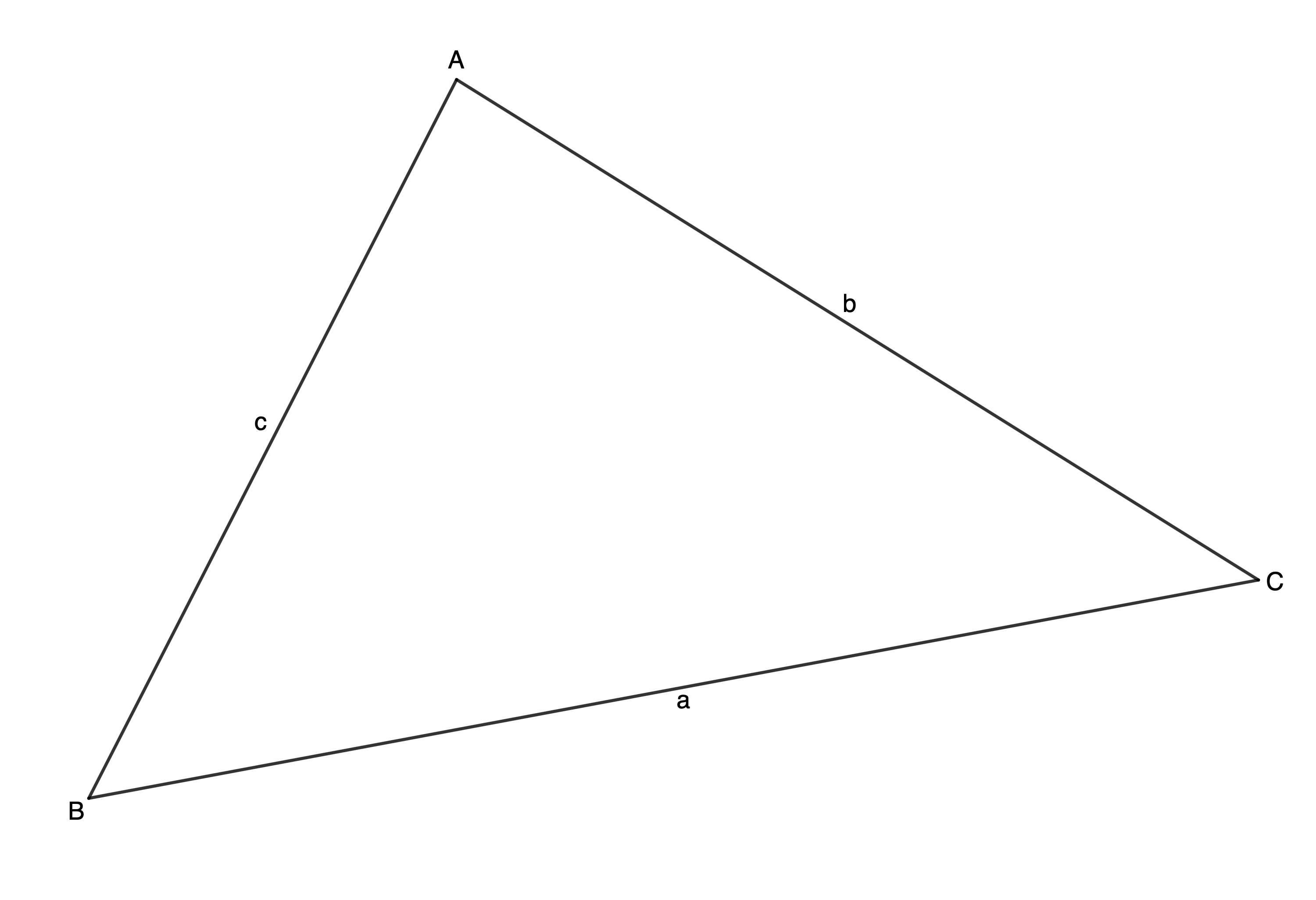
1. [latex]\scriptsize CP[/latex] is a radio mast. [latex]\scriptsize CA[/latex] and [latex]\scriptsize CB[/latex] are cables used to support the mast. [latex]\scriptsize B[/latex] and [latex]\scriptsize A[/latex] are on the same level as [latex]\scriptsize P[/latex]. [latex]\scriptsize CA=11\ \text{m}[/latex], [latex]\scriptsize CB=8\ \text{m}[/latex] and [latex]\scriptsize BA=10\ \text{m}[/latex].
   1. Determine [latex]\scriptsize C\hat{A}B[/latex].
   2. Hence, determine [latex]\scriptsize CP[/latex].
   3. Determine the area of [latex]\scriptsize \Delta CAB[/latex].
2. The diagram below shows a [latex]\scriptsize 34\ \text{m}[/latex] vertical observation tower [latex]\scriptsize AT[/latex] , and two cars, [latex]\scriptsize B[/latex] and [latex]\scriptsize C[/latex], on a road. The angle of depression from [latex]\scriptsize T[/latex] to car [latex]\scriptsize C[/latex] is [latex]\scriptsize {{32}^\circ}[/latex]. The angle of elevation from car [latex]\scriptsize B[/latex] to the top of the tower is [latex]\scriptsize {{45}^\circ}[/latex].[latex]\scriptsize A[/latex], [latex]\scriptsize B[/latex] and [latex]\scriptsize C[/latex] lie in a straight line and lie on the same horizontal plane as the base of the tower.
   
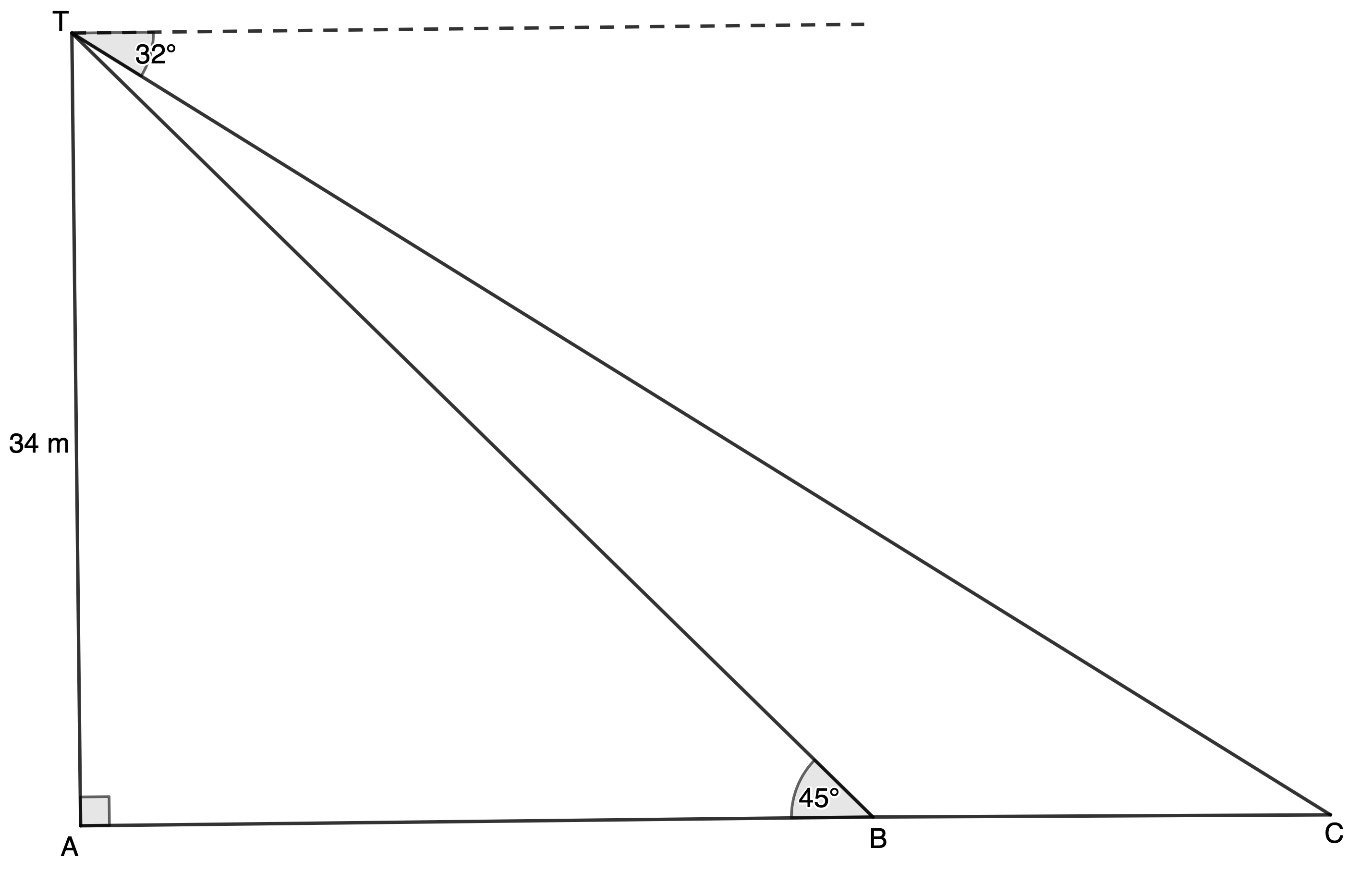
   1. Calculate the size of [latex]\scriptsize \hat{C}[/latex].
   2. Determine the length of [latex]\scriptsize BT[/latex].
   3. Hence, calculate the distance between the two cars.
3. A piece of land has the form of a quadrilateral [latex]\scriptsize ABCD[/latex] as shown below. All distances are in kilometres.
   
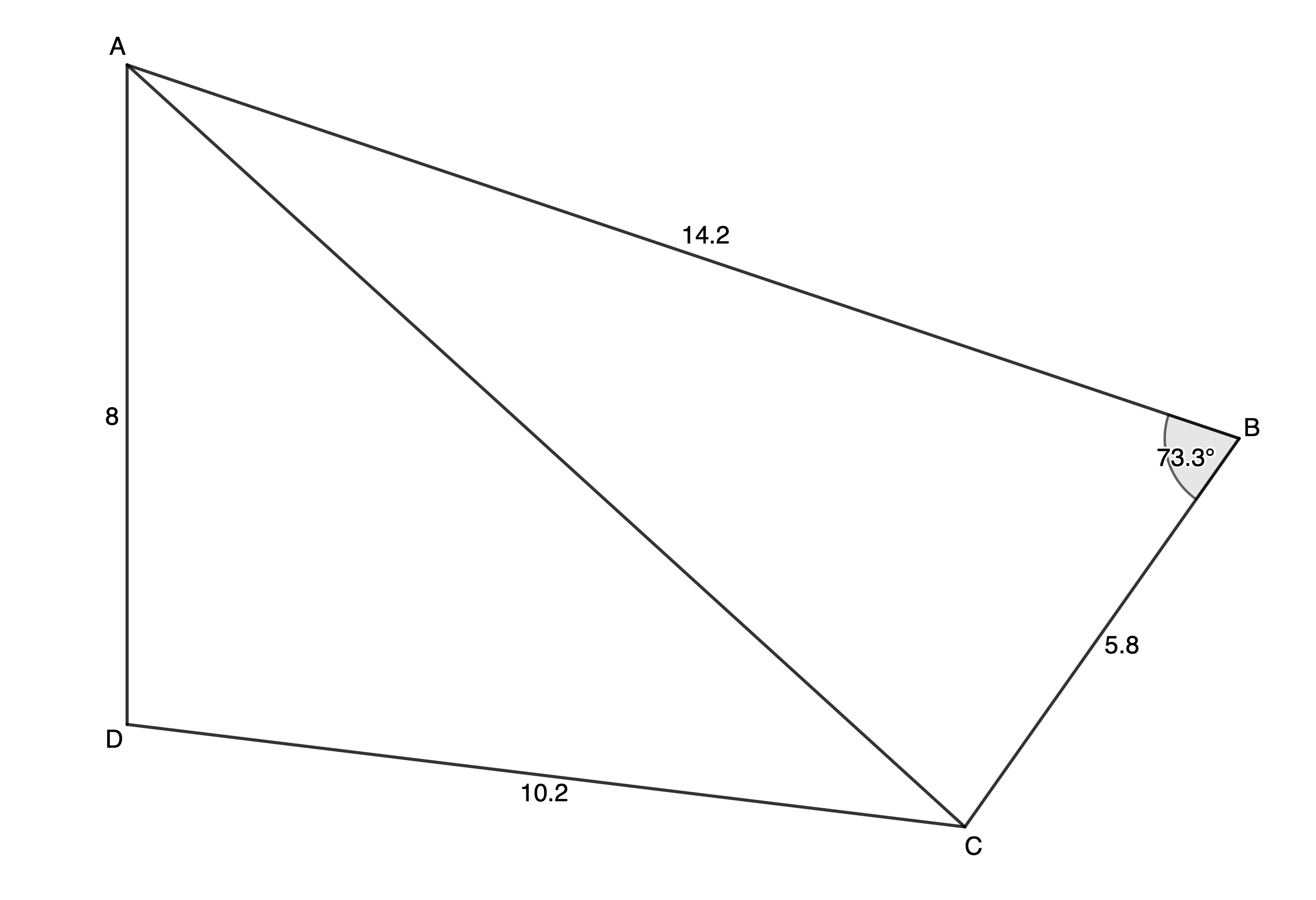
   The owner decides to divide the land into two plots by erecting a fence from [latex]\scriptsize A[/latex] to [latex]\scriptsize C[/latex].
   1. Calculate the length of the fence [latex]\scriptsize AC[/latex] correct to one decimal place.
   2. Calculate the size of [latex]\scriptsize B\hat{A}C[/latex] correct to the nearest degree.
   3. Calculate the size of [latex]\scriptsize \hat{D}[/latex], correct to the nearest degree.
   4. Calculate the area of the entire piece of land [latex]\scriptsize ABCD[/latex], correct to one decimal place.

The full solutions are at the end of the unit.

Summary

In this unit you have learnt the following:

• How to solve 2-D trigonometry problems using a combination of the area rule, sine rule and cosine rule.

Unit 8: Assessment

Suggested time to complete: 45 minutes

1. [latex]\scriptsize \Delta PQR[/latex] is an isosceles triangle with [latex]\scriptsize PQ=QR[/latex]. By using the cosine rule, prove that [latex]\scriptsize \cos Q=1-\displaystyle \frac{{{{q}^{2}}}}{{2{{p}^{2}}}}[/latex].
   
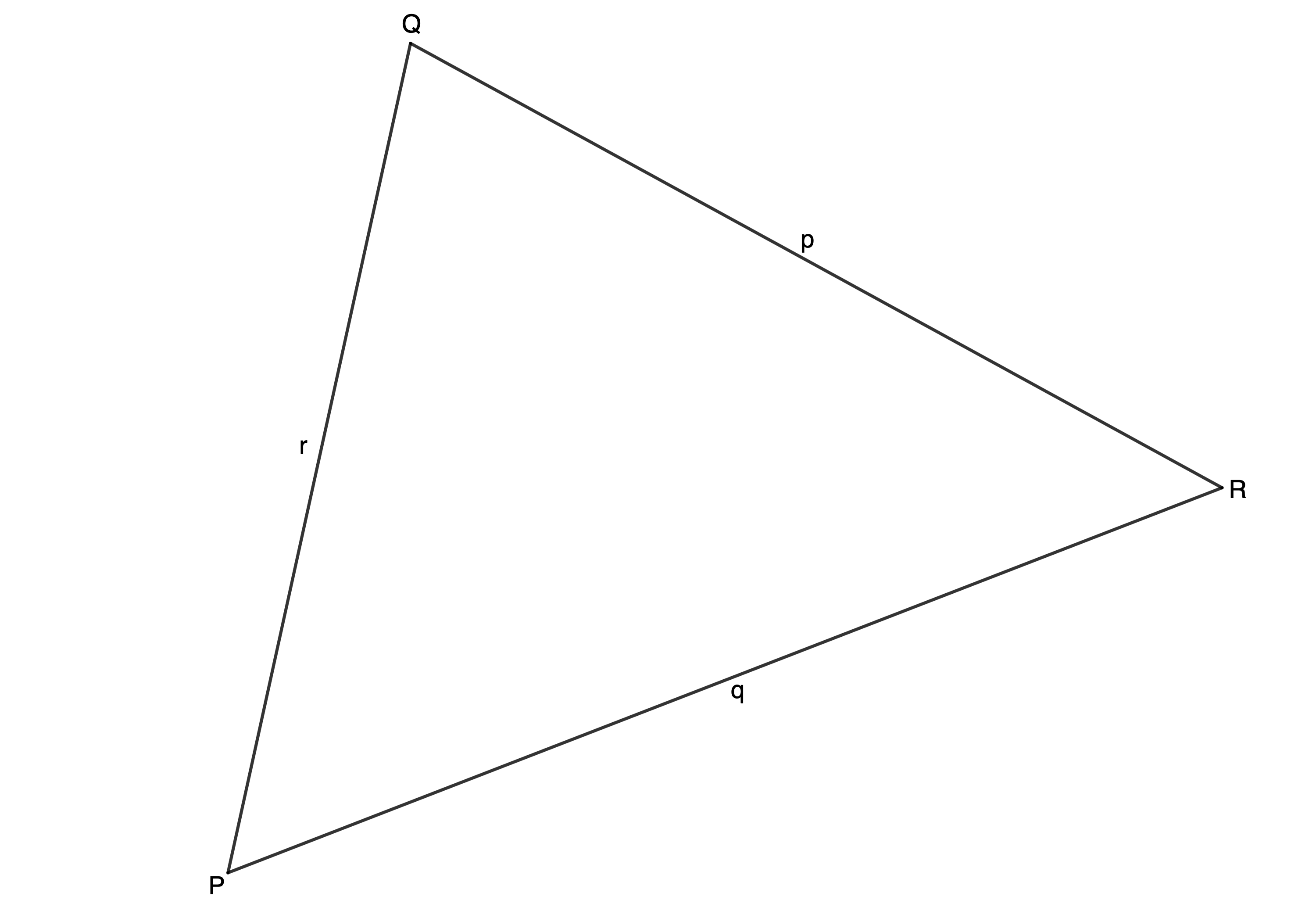
2. If [latex]\scriptsize b=c[/latex] and [latex]\scriptsize {{a}^{2}}=7{{b}^{2}}[/latex], show why it is impossible to construct [latex]\scriptsize \Delta ABC[/latex].
   
3. A game ranger [latex]\scriptsize M[/latex] is [latex]\scriptsize 10.9\ \text{km}[/latex] from control centre [latex]\scriptsize O[/latex] at a bearing of [latex]\scriptsize {{55}^\circ}[/latex], when he receives a call that there is an elephant at [latex]\scriptsize P[/latex], injured and needing attention as a result of a failed poaching attempt. The elephant is located [latex]\scriptsize 9.2\ \text{km}[/latex] at [latex]\scriptsize \text{E}{{15}^\circ}\text{S}[/latex] of the control centre. The diagram below is a representation of the situation.
   
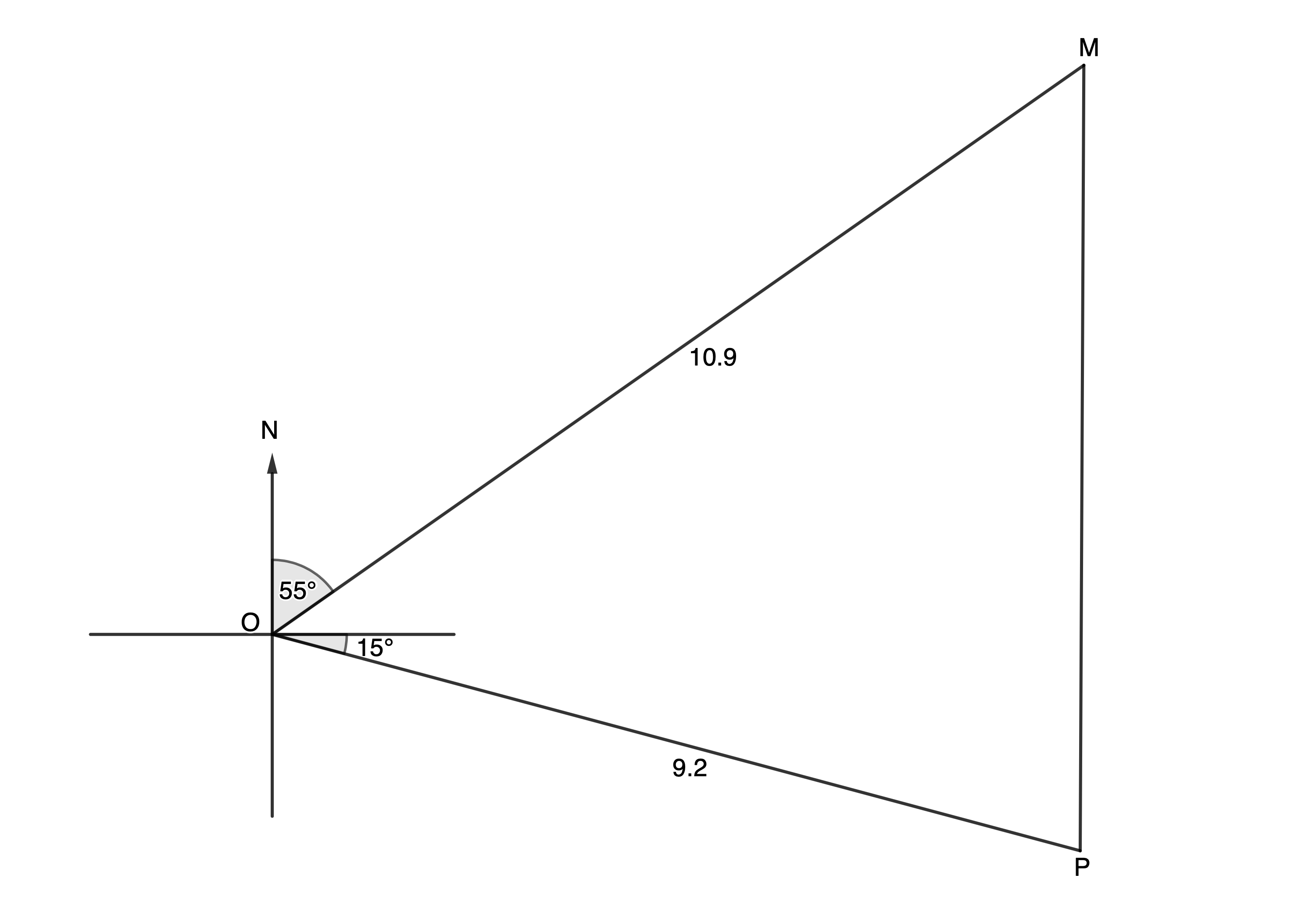
   1. Determine how far the game ranger is from the injured elephant.
   2. If it is believed that the poachers are in the area formed by [latex]\scriptsize \Delta MOP[/latex], calculate the area that needs to be searched.
4. Two ships, [latex]\scriptsize A[/latex] and [latex]\scriptsize B[/latex], are [latex]\scriptsize 155\ \text{km}[/latex] apart. Ship [latex]\scriptsize A[/latex] is at a bearing of [latex]\scriptsize {{67}^\circ}[/latex] from [latex]\scriptsize D[/latex] and [latex]\scriptsize 93\ \text{km}[/latex] away from [latex]\scriptsize D[/latex]. [latex]\scriptsize DN[/latex] points due north. Ship [latex]\scriptsize B[/latex] is at a bearing of [latex]\scriptsize {{208}^\circ}[/latex] from [latex]\scriptsize D[/latex].
   
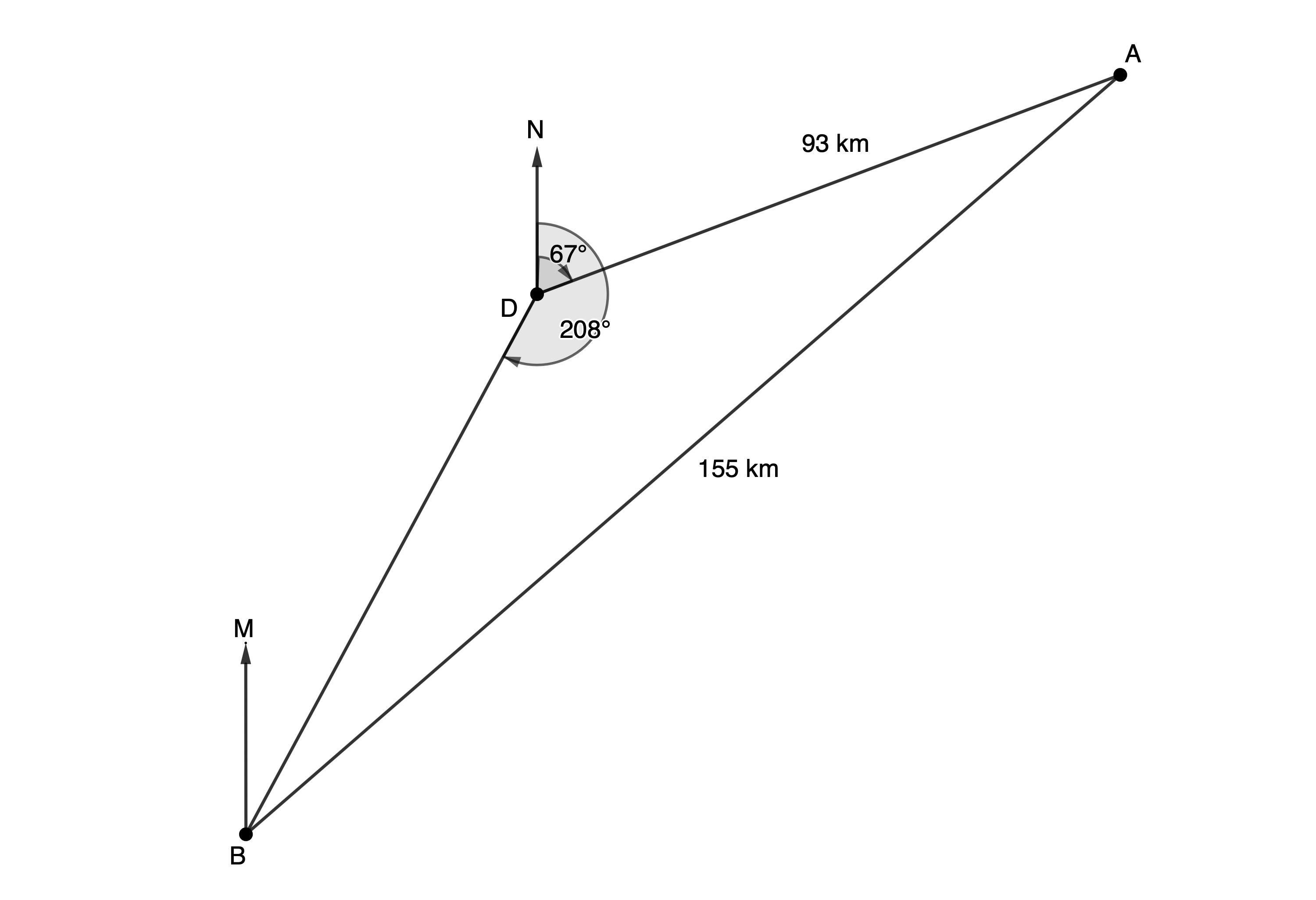
   1. Determine the bearing of Ship [latex]\scriptsize A[/latex] from Ship [latex]\scriptsize B[/latex], when [latex]\scriptsize BM\parallel DN[/latex].
   2. If Ship [latex]\scriptsize B[/latex] travels due north, and Ship [latex]\scriptsize A[/latex] travels due south, then at some instant in time, Ship [latex]\scriptsize A[/latex] is due east of Ship [latex]\scriptsize B[/latex]. Calculate the distance between the two ships at that instant.

The full solutions are at the end of the unit.

Unit 8: Solutions

Exercise 8.1

1. Start by making a sketch of the given information.
   
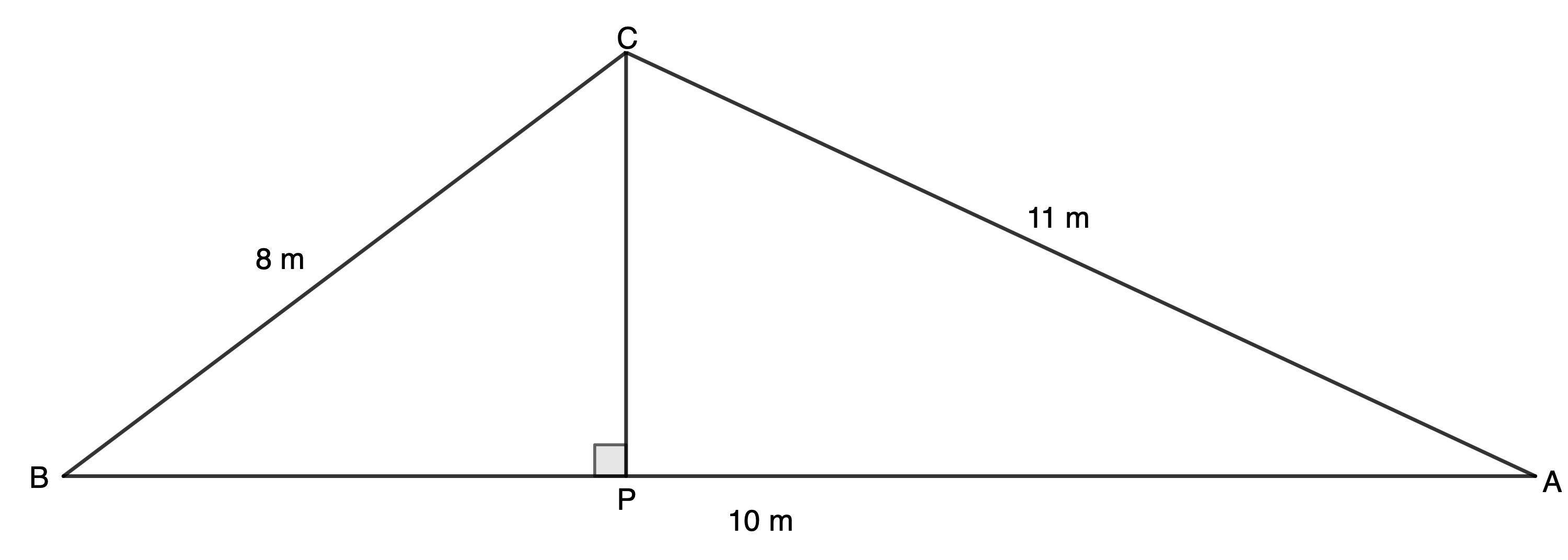
   1. [latex]\scriptsize C\hat{A}B=\hat{A}[/latex]
      [latex]\scriptsize \begin{align*}B{{C}^{2}} & =A{{B}^{2}}+A{{C}^{2}}-2\cdot AB\cdot AC\cdot \cos A\\\therefore \cos A & =\displaystyle \frac{{A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}}}}{{2\cdot AB\cdot AC}}\\ & =\displaystyle \frac{{{{{10}}^{2}}+{{{11}}^{2}}-{{8}^{2}}}}{{2\times 10\times 11}}\\\therefore A & ={{44.47}^\circ}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{CP}}{{\sin A}} & =\displaystyle \frac{{AC}}{{\sin A\hat{P}C}}\\\therefore \displaystyle \frac{{CP}}{{\sin {{{44.47}}^\circ}}} & =\displaystyle \frac{{11}}{{\sin {{{90}}^\circ}}}\\\therefore CP & =\displaystyle \frac{{11\sin {{{44.47}}^\circ}}}{{\sin {{{90}}^\circ}}}\\ & =7.71\ \text{m}\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}\text{area }\Delta ABC&=\displaystyle \frac{1}{2}\times AC\times AB\times \sin A\\ &=\displaystyle \frac{1}{2}\times 11\times 10\times \sin44.47^\circ\\ &=38.53\text{ m}^2 \end{align*}[/latex]
2. .
   1. [latex]\scriptsize AC[/latex] is parallel to the horizontal line from which the angle of depression to car [latex]\scriptsize C[/latex] is measured. Therefore, [latex]\scriptsize \hat{C}={{32}^\circ}[/latex] (alternate angles are equal)
   2. In [latex]\scriptsize \Delta ABT[/latex]:
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{BT}}{{\sin A}} & =\displaystyle \frac{{AT}}{{\sin A\hat{B}T}}\\\therefore \displaystyle \frac{{BT}}{{\sin {{{90}}^\circ}}} & =\displaystyle \frac{{34}}{{\sin {{{45}}^\circ}}}\\\therefore BT & =\displaystyle \frac{{34\sin {{{90}}^\circ}}}{{\sin {{{45}}^\circ}}}\\ & =48.08\ \text{m}\end{align*}[/latex]
   3. [latex]\scriptsize A\hat{T}B={{180}^\circ}-{{90}^\circ}-{{45}^\circ}={{45}^\circ}[/latex] (angles in a triangle are supplementary)
      [latex]\scriptsize B\hat{T}C={{90}^\circ}-A\hat{T}B-{{32}^\circ}={{90}^\circ}-{{45}^\circ}-{{32}^\circ}={{13}^\circ}[/latex]
      In [latex]\scriptsize \Delta BCT[/latex]:
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{BC}}{{\sin B\hat{T}C}} & =\displaystyle \frac{{BT}}{{\sin C}}\\\therefore \displaystyle \frac{{BC}}{{\sin {{{13}}^\circ}}} & =\displaystyle \frac{{48.08}}{{\sin {{{32}}^\circ}}}\\\therefore BC & =\displaystyle \frac{{48.08\sin {{{13}}^\circ}}}{{\sin {{{32}}^\circ}}}\\ & =20.41\ \text{m}\end{align*}[/latex]
3. .
   1. .
      [latex]\scriptsize \begin{align*}A{{C}^{2}} & =A{{B}^{2}}+B{{C}^{2}}-2\cdot AB\cdot BC\cdot \cos B\\\therefore A{{C}^{2}} & ={{14.2}^{2}}+{{5.8}^{2}}-2\cdot (14.2)\cdot (5.8)\cdot \cos {{73.3}^\circ}\\\therefore AC & =\sqrt{{{{{14.2}}^{2}}+{{{5.8}}^{2}}-2\cdot (14.2)\cdot (5.8)\cdot \cos {{{73.3}}^\circ}}}\\ & =13.7\ \text{km}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin B\hat{A}C}}{{BC}}&=\displaystyle \frac{{\sin B}}{{AC}}\\\therefore \displaystyle \frac{{\sin B\hat{A}C}}{{5.8}}&=\displaystyle \frac{{\sin {{{73.3}}^\circ}}}{{13.71}}\\\therefore \sin B\hat{A}C&=\displaystyle \frac{{5.8\sin {{{73.3}}^\circ}}}{{13.71}}\\\therefore B\hat{A}C&={{24}^\circ}\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}A{{C}^{2}} & =A{{D}^{2}}+C{{D}^{2}}-2\cdot AD\cdot CD\cdot \cos D\\\therefore \cos D & =\displaystyle \frac{{A{{D}^{2}}+C{{D}^{2}}-A{{C}^{2}}}}{{2\cdot AD\cdot CD}}\\\therefore \cos D & =\displaystyle \frac{{{{8}^{2}}+{{{10.2}}^{2}}-{{{13.7}}^{2}}}}{{2\cdot 8\cdot (10.2)}}\\\therefore \hat{D} & ={{97}^\circ}\end{align*}[/latex]
   4. [latex]\scriptsize \text{area }\Delta ABCD=\text{area }\Delta ABC+\text{area }\Delta ACD[/latex]
      [latex]\scriptsize \begin{align*}\text{area }\Delta ABC&=\displaystyle \frac{1}{2}\cdot AB\cdot BC\cdot \sin B\\&=\displaystyle \frac{1}{2}\cdot (14.2)\cdot (5.8)\cdot \sin {{73.3}^\circ}\\&=39.4\ \text{k}{{\text{m}}^{2}}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}\text{area }\Delta ACD&=\displaystyle \frac{1}{2}\cdot AD\cdot CD\cdot \sin D\\&=\displaystyle \frac{1}{2}\cdot 8\cdot (10.2)\cdot \sin {{97}^\circ}\\&=40.5\ \text{k}{{\text{m}}^{2}}\end{align*}[/latex]
      [latex]\scriptsize \text{area }ABCD=39.4+40.5=79.9\ \text{k}{{\text{m}}^{2}}[/latex]

Back to Exercise 8.1

Unit 8: Assessment

1. To prove: [latex]\scriptsize \cos Q=1-\displaystyle \frac{{{{q}^{2}}}}{{2{{p}^{2}}}}[/latex] using the cosine rule.
   [latex]\scriptsize \begin{align*}{{q}^{2}} & ={{p}^{2}}+{{r}^{2}}-2pr\cos Q\\\therefore \cos Q & =\displaystyle \frac{{{{p}^{2}}+{{r}^{2}}-{{q}^{2}}}}{{2pr}}\\\text{But: }PQ & =QR\therefore p =r\\\therefore \cos Q & =\displaystyle \frac{{{{p}^{2}}+{{p}^{2}}-{{q}^{2}}}}{{2p\cdot p}}\\&=\displaystyle \frac{{2{{p}^{2}}-{{q}^{2}}}}{{2{{p}^{2}}}}\\&=\displaystyle \frac{{2{{p}^{2}}}}{{2{{p}^{2}}}}-\displaystyle \frac{{{{q}^{2}}}}{{2{{p}^{2}}}}\\&=1-\displaystyle \frac{{{{q}^{2}}}}{{2{{p}^{2}}}}\end{align*}[/latex]
2. [latex]\scriptsize b=c[/latex] and [latex]\scriptsize {{a}^{2}}=7{{b}^{2}}[/latex], and assume one can construct [latex]\scriptsize \Delta ABC[/latex]. Then:
   [latex]\scriptsize \begin{align*}{{a}^{2}} & ={{b}^{2}}+{{c}^{2}}-2bc\cos A\\\text{But: }{{a}^{2}}=7{{b}^{2}}\text{ and }b=c\\\therefore 7{{b}^{2}} & ={{b}^{2}}+{{b}^{2}}-2{{b}^{2}}\cos A\\\therefore 7{{b}^{2}} & =2{{b}^{2}}-2{{b}^{2}}\cos A\\\therefore 7{{b}^{2}} & =2{{b}^{2}}(1-\cos A)\\\therefore \displaystyle \frac{{7\bcancel{{{{b}^{2}}}}}}{{2\bcancel{{{{b}^{2}}}}}} & =1-\cos A\\\therefore \cos A & =1-\displaystyle \frac{7}{2}=-\displaystyle \frac{5}{2}\end{align*}[/latex]
   But [latex]\scriptsize \cos A[/latex] cannot be less than [latex]\scriptsize -1[/latex]. Therefore, the construction is not possible.
3. .
   1. [latex]\scriptsize M\hat{O}P=({{90}^\circ}-{{55}^\circ})+{{15}^\circ}={{50}^\circ}[/latex]
      [latex]\scriptsize \begin{align*}M{{P}^{2}} & =M{{O}^{2}}+P{{O}^{2}}-2\cdot MO\cdot PO\cdot \cos M\hat{O}N\\\therefore M{{P}^{2}} & ={{10.9}^{2}}+{{9.2}^{2}}-2\cdot (10.9)\cdot (9.2)\cdot \cos {{50}^\circ}\\\therefore MP & =\sqrt{{{{{10.9}}^{2}}+{{{9.2}}^{2}}-2\cdot (10.9)\cdot (9.2)\cdot \cos {{{50}}^\circ}}}\\ & =8.63\ \text{km}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\text{area }\Delta MOP&=\displaystyle \frac{1}{2}\cdot MO\cdot PO\cdot \sin M\hat{O}N\\&=\displaystyle \frac{1}{2}\cdot (10.9)\cdot (9.2)\cdot \sin {{50}^\circ}\\&=38.41\ \text{k}{{\text{m}}^{2}}\end{align*}[/latex]
4. A sketch of the information was given.
   
   1. The bearing of Ship [latex]\scriptsize A[/latex] from Ship [latex]\scriptsize B[/latex] is [latex]\scriptsize M\hat{B}A[/latex].
      [latex]\scriptsize M\hat{B}A=D\hat{B}M+A\hat{B}D[/latex]
      [latex]\scriptsize N\hat{D}B={{360}^\circ}-{{208}^\circ}={{152}^\circ}[/latex] (angles at a point)
      [latex]\scriptsize BM\parallel DN[/latex] (given). Therefore, [latex]\scriptsize D\hat{B}M={{180}^\circ}-{{152}^\circ}={{28}^\circ}[/latex] (co-interior angles are supplementary, [latex]\scriptsize BM\parallel DN[/latex])
      In [latex]\scriptsize \Delta ADB[/latex]:
      [latex]\scriptsize A\hat{D}B={{208}^\circ}-{{67}^\circ}={{141}^\circ}[/latex]
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin A\hat{B}D}}{{AD}}&=\displaystyle \frac{{\sin A\hat{D}B}}{{AB}}\\\therefore \displaystyle \frac{{\sin A\hat{B}D}}{{93}}&=\displaystyle \frac{{\sin {{{141}}^\circ}}}{{155}}\\\therefore \sin A\hat{B}D&=\displaystyle \frac{{93\sin {{{141}}^\circ}}}{{155}}\\\therefore A\hat{B}D&={{22.18}^\circ}\end{align*}[/latex][latex]\scriptsize M\hat{B}A=28{}^\circ +22.18{}^\circ =50.18{}^\circ[/latex]
   2. It helps to makes another sketch to see what is happening.
      
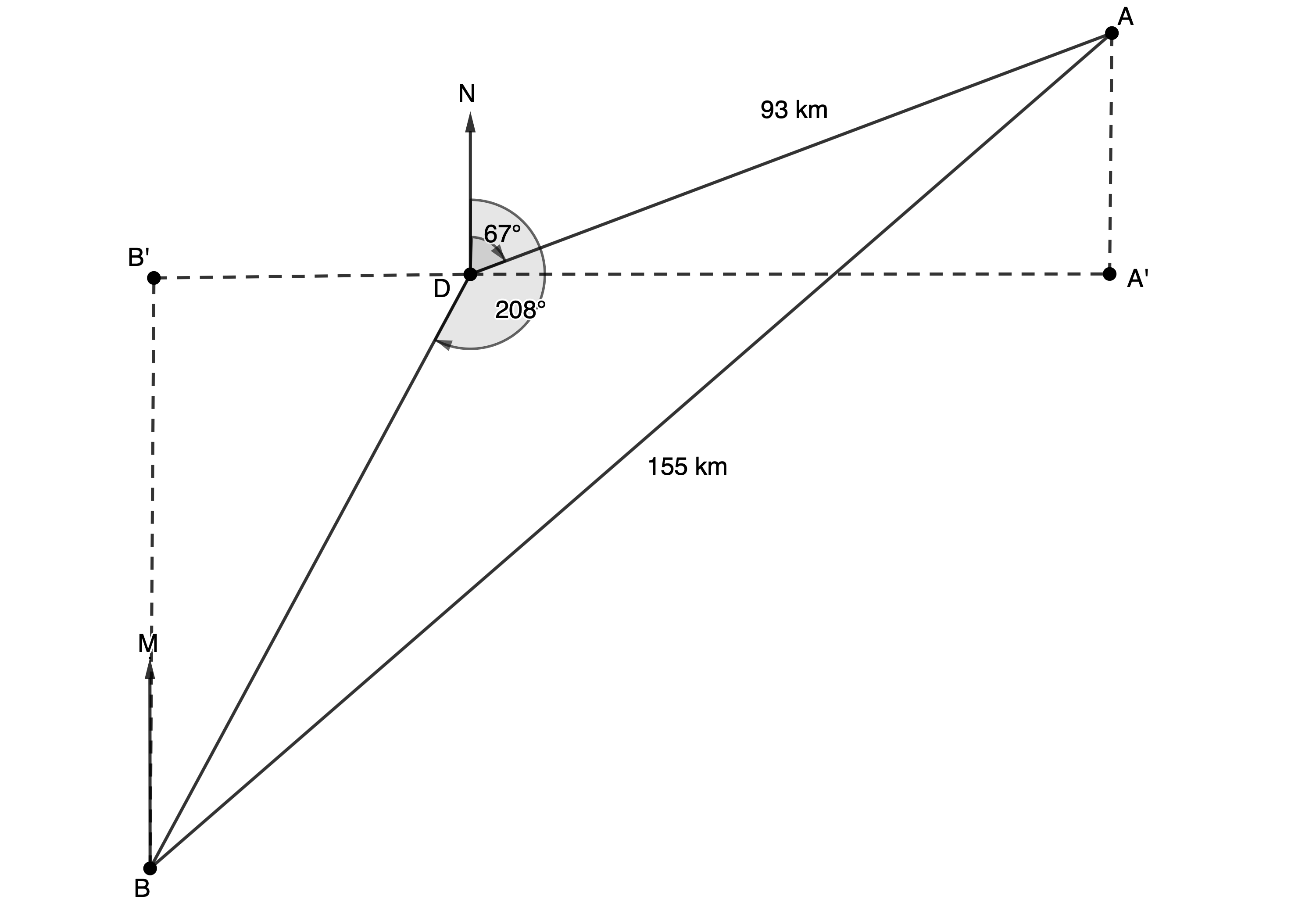
      The sketch shows when Ship [latex]\scriptsize A[/latex] is due east of Ship [latex]\scriptsize B[/latex]. We need to determine that the length of [latex]\scriptsize A'B'[/latex] which is equal to [latex]\scriptsize A'D+B'D[/latex]. Because we are told that the ships sail due north and due south respectively, we know that we are dealing with right-angled triangles.
      .
      In [latex]\scriptsize \Delta ADA'[/latex]:
      [latex]\scriptsize A\hat{D}A'={{90}^\circ}-{{67}^\circ}={{23}^\circ}[/latex]
      [latex]\scriptsize \begin{align*}\cos {{23}^\circ} & =\displaystyle \frac{{DA'}}{{93}}\\\therefore DA' & =93\cos {{23}^\circ}\\ & =85.61\ \text{km}\end{align*}[/latex]
      To determine [latex]\scriptsize B'D[/latex], we need the length of [latex]\scriptsize BD[/latex]. To determine [latex]\scriptsize BD[/latex], we need to determine [latex]\scriptsize D\hat{A}B[/latex].
      .
      In [latex]\scriptsize \Delta ABD[/latex]:
      [latex]\scriptsize A\hat{B}D={{22.18}^\circ}[/latex] (from a.)
      [latex]\scriptsize \begin{align*}\therefore D\hat{A}B&={{180}^\circ}-A\hat{D}B-A\hat{B}D&&\text{(angles in a triangle are supplementary)}\\&={{180}^\circ}-{{141}^\circ}-{{22.18}^\circ}\\&={{16.82}^\circ}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}\displaystyle \frac{{BD}}{{\sin D\hat{A}B}} & =\displaystyle \frac{{AB}}{{\sin A\hat{D}B}}\\\therefore \displaystyle \frac{{BD}}{{\sin {{{16.82}}^\circ}}} & =\displaystyle \frac{{155}}{{\sin {{{141}}^\circ}}}\\\therefore BD & =\displaystyle \frac{{155\sin {{{16.82}}^\circ}}}{{\sin {{{141}}^\circ}}}\\ & =71.27\ \text{km}\end{align*}[/latex]
      .
      In [latex]\scriptsize \Delta BDB'[/latex]:
      [latex]\scriptsize B\hat{D}B'={{270}^\circ}-{{208}^\circ}={{62}^\circ}[/latex]
      [latex]\scriptsize \begin{align*}\cos {{62}^\circ} & =\displaystyle \frac{{DB'}}{{BD}}\\\therefore DB' & =71.27\cos {{62}^\circ}\\ & =33.46\ \text{km}\end{align*}[/latex]
      .
      Therefore:
      [latex]\scriptsize \begin{align*}A'B'=85.61+33.46\\=119.07\ \text{km}\end{align*}[/latex]

Back to Unit 8: Assessment