Space, shape and measurement: Solve problems by constructing and interpreting trigonometric models
Unit 1: Special angles
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Simplify trigonometric ratios involving the angles [latex]\scriptsize {{30}^\circ}[/latex], [latex]\scriptsize {{45}^\circ}[/latex] and [latex]\scriptsize {{60}^\circ}[/latex].
What you should know
Before you start this unit, make sure you can:
- Define the three basic trigonometric ratios of sine, cosine and tangent. Refer to level 2 subject outcome 3.6 unit 1 if you need help with this.
Introduction
We know by now that the trigonometric, or trig, ratios of sine, cosine and tangent define the ratios of sides in a right-angled triangle in relation to its angles. In the following triangle, for example, the three basic trig ratios are:
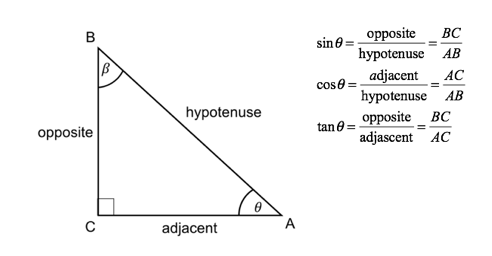
Most of the time, we need a calculator to work out what these ratios are. However, there are some special angles that give us ‘nice’ answers. You may have encountered these special angles in previous units. These angles come up so often that it is very worthwhile just remembering their trig ratios. This unit is all about these special angles.
The special angles
There are three special angles. They are [latex]\scriptsize {{30}^\circ}[/latex], [latex]\scriptsize {{45}^\circ}[/latex] and [latex]\scriptsize {{60}^\circ}[/latex]. They are special because they provide complementary pairs of angles ([latex]\scriptsize 30{}^\circ[/latex] and [latex]\scriptsize {{60}^\circ}[/latex], and [latex]\scriptsize {{45}^\circ}[/latex] and [latex]\scriptsize {{45}^\circ}[/latex]) for right-angled triangles. Trig ratios can easily be read off right-angled triangles, which can also be solved using Pythagoras’ Theorem.
Activity 1.1: Special angles
Time required: 15 minutes
What you need:
- a pen or pencil
- a blank piece of paper
- a ruler
- a protractor
What to do:
In this activity we are going to discover why the angles of [latex]\scriptsize {{30}^\circ}[/latex], [latex]\scriptsize {{45}^\circ}[/latex] and [latex]\scriptsize {{60}^\circ}[/latex] are considered ‘special angles’.
- On your piece of paper, draw a right-angled triangle with a [latex]\scriptsize {{30}^\circ}[/latex] angle in it making sure that the length of the side opposite the [latex]\scriptsize {{30}^\circ}[/latex] angle is a whole number.
- Measure the length of the hypotenuse of this triangle.
- Write down the value of [latex]\scriptsize \sin {{30}^\circ}[/latex] .
- Calculate, using the theorem of Pythagoras what the length of the side adjacent to the [latex]\scriptsize {{30}^\circ}[/latex] angle is.
- Write down the values of [latex]\scriptsize \cos {{30}^\circ}[/latex] and [latex]\scriptsize \tan {{30}^\circ}[/latex].
- Now write down what [latex]\scriptsize \sin {{60}^\circ}[/latex], [latex]\scriptsize \cos {{60}^\circ}[/latex] and [latex]\scriptsize \tan {{60}^\circ}[/latex] are. Do you need to draw a new triangle?
- On your piece of paper, draw another right-angled triangle with a [latex]\scriptsize {{45}^\circ}[/latex] angle in it, making sure that the length of the side opposite this [latex]\scriptsize {{45}^\circ}[/latex] angle is a whole number.
- What is the size of the other angle?
- Measure, or work out using the theorem of Pythagoras, what the lengths of the other two sides are and write down the values of [latex]\scriptsize \sin {{45}^\circ}[/latex], [latex]\scriptsize \cos {{45}^\circ}[/latex] and [latex]\scriptsize \tan {{45}^\circ}[/latex].
What did you find?
- Let’s assume that we drew a triangle like this where the side opposite the [latex]\scriptsize {{30}^\circ}[/latex] angle was [latex]\scriptsize 10\ \text{cm}[/latex] (see Figure 2).
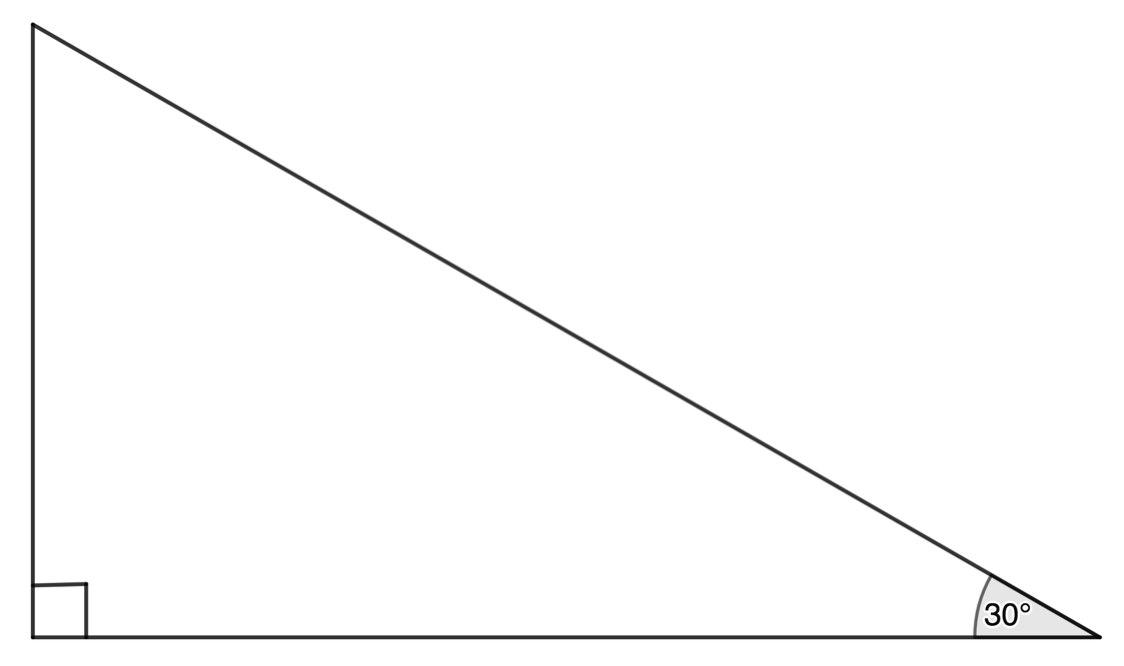
Figure 2: Right-angled triangle with a [latex]\scriptsize {{30}^\circ}[/latex] angle - You should find that the hypotenuse is exactly double the length of the side opposite the [latex]\scriptsize {{30}^\circ}[/latex] angle. In our case, it is [latex]\scriptsize 20\ \text{cm}[/latex].
- [latex]\scriptsize \sin {{30}^\circ}=\displaystyle \frac{1}{2}[/latex]. Remember, it does not matter how big your triangle is. The length of the side opposite the angle and the hypotenuse are always in the same ratio. When the angle is [latex]\scriptsize {{30}^\circ}[/latex], this ratio is [latex]\scriptsize \displaystyle \frac{1}{2}[/latex].
- Using Pythagoras, the length of the side adjacent to the [latex]\scriptsize {{30}^\circ}[/latex] angle is [latex]\scriptsize \sqrt{3}[/latex] or some multiple of [latex]\scriptsize \sqrt{3}[/latex] depending on how big your triangle is.
- [latex]\scriptsize \cos {{30}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex]. Remember, it does not matter how big your triangle is. The length of the side adjacent the angle and the hypotenuse are always in the same ratio. When the angle is [latex]\scriptsize {{30}^\circ}[/latex], this ratio is [latex]\scriptsize \displaystyle \frac{{\sqrt{3}}}{2}[/latex].
[latex]\scriptsize \tan {{30}^\circ}=\displaystyle \frac{1}{{\sqrt{3}}}[/latex]. Remember, it does not matter how big your triangle is. The length of the side adjacent the angle and the hypotenuse are always in the same ratio. When the angle is [latex]\scriptsize {{30}^\circ}[/latex], this ratio is [latex]\scriptsize \displaystyle \frac{1}{{\sqrt{3}}}[/latex]. - The other angle in our triangle is [latex]\scriptsize {{60}^\circ}[/latex] so we can just use this as our reference angle (see Figure 3). Now
[latex]\scriptsize \sin {{60}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex], [latex]\scriptsize \cos {{60}^\circ}=\displaystyle \frac{1}{2}[/latex] and [latex]\scriptsize \tan {{60}^\circ}=\displaystyle \frac{{\sqrt{3}}}{1}[/latex].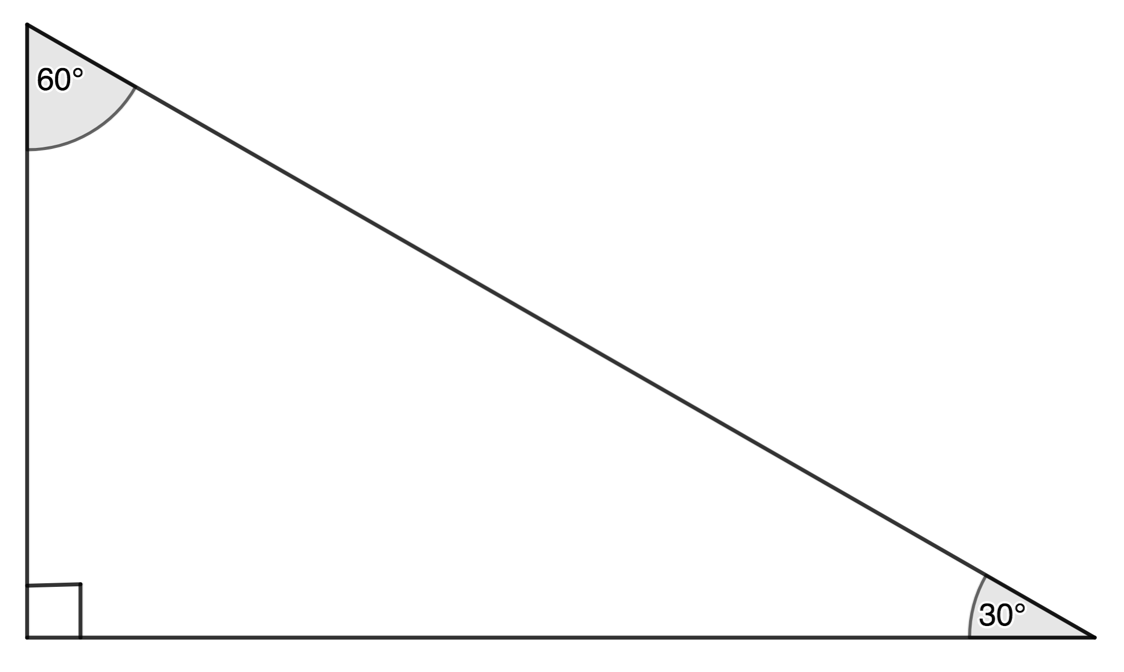
Figure 3: The other angle in the triangle is [latex]\scriptsize {{60}^\circ}[/latex] - Let’s assume that we drew a triangle like this where the side opposite the [latex]\scriptsize {{45}^\circ}[/latex] angle was [latex]\scriptsize 10\ \text{cm}[/latex] (see Figure 4).
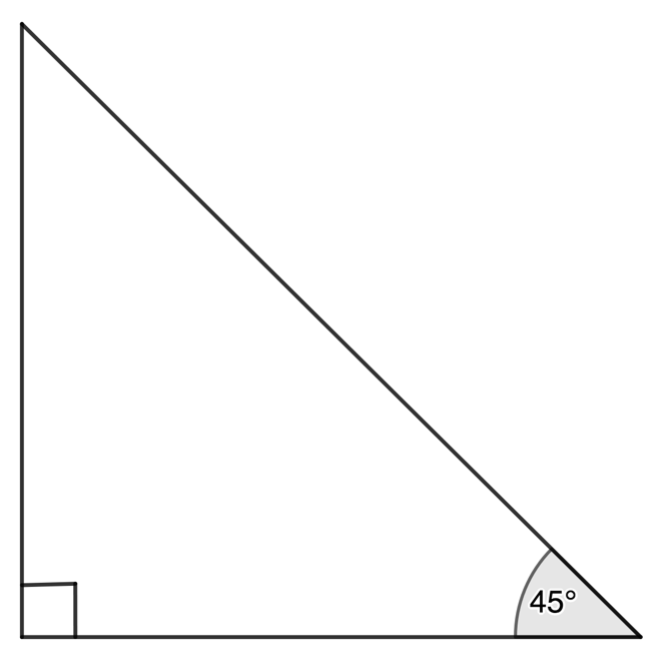
Figure 4: Right-angled triangle with a [latex]\scriptsize {{45}^\circ}[/latex] angle - The other angle is also [latex]\scriptsize {{45}^\circ}[/latex].
- You will find that the three trig ratios are [latex]\scriptsize \sin {{45}^\circ}=\displaystyle \frac{1}{{\sqrt{2}}}[/latex], [latex]\scriptsize \cos {{45}^\circ}=\displaystyle \frac{1}{{\sqrt{2}}}[/latex] and [latex]\scriptsize \tan {{45}^\circ}=1[/latex].
We have discovered the three basic trig ratios for the angles [latex]\scriptsize {{30}^\circ}[/latex], [latex]\scriptsize {{45}^\circ}[/latex] and [latex]\scriptsize {{60}^\circ}[/latex]. Remember that it does not matter how big the triangles are. The sides will always be in the same ratio. This ratio depends only on the angle.
Special angles:
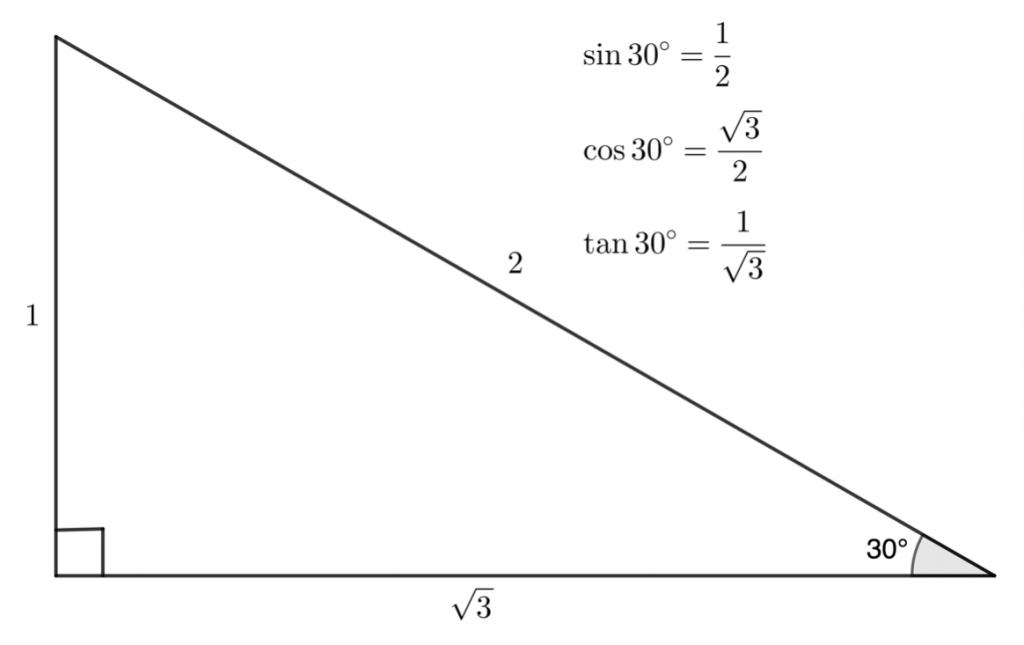
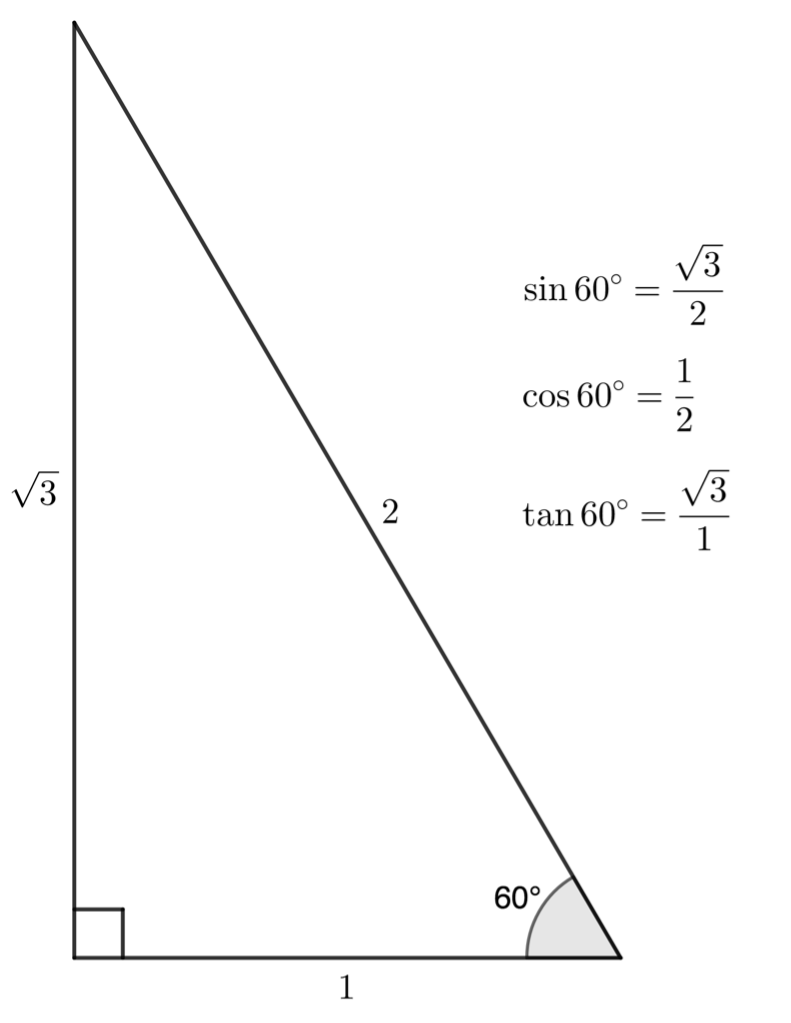
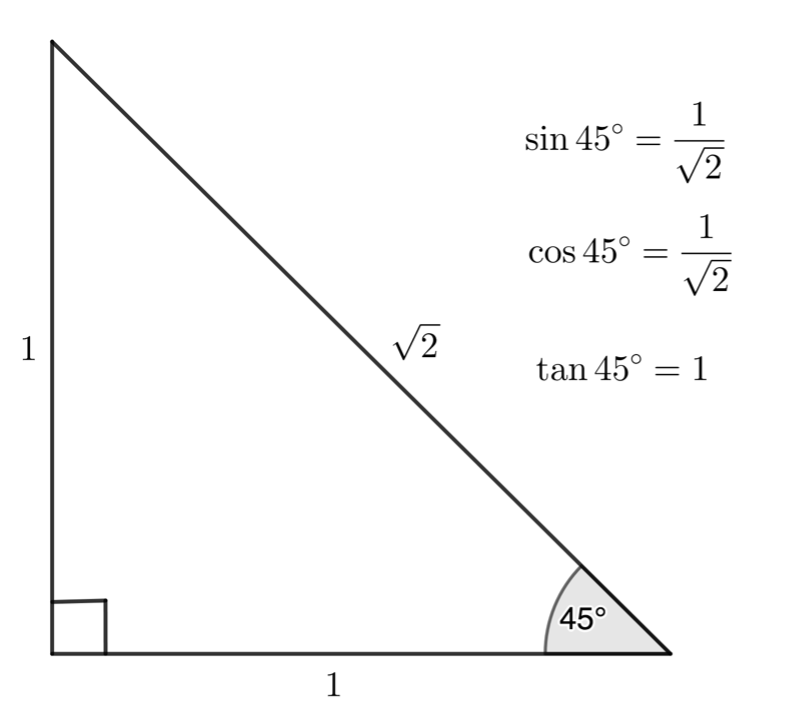
Simplify trig expressions with special angles
Note
If you ever come across a question requiring the calculation of values of trig ratios ‘without a calculator’, you know that you will be dealing with the trig ratios of these three special angles.
Example 1.1
Simplify the following trig expression without a calculator, leaving your answer in simplest surd form: [latex]\scriptsize \sin {{45}^\circ}+\sin {{30}^\circ}[/latex].
Solution
We are told that we may not use a calculator. Therefore, we need to use the special angle ratios.
[latex]\scriptsize \begin{align*}\sin {{45}^\circ}+\sin {{30}^\circ}&=\displaystyle \frac{1}{{\sqrt{2}}}+\displaystyle \frac{1}{2}\text{ }\\&=\displaystyle \frac{{2+\sqrt{2}}}{{2\sqrt{2}}}&&\text{We prefer not to have surds in the denominator, so multiply by }\displaystyle \frac{{\sqrt{2}}}{{\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{2}\times \left( {2+\sqrt{2}} \right)}}{{\sqrt{2}\times 2\sqrt{2}}}\\&=\displaystyle \frac{{2\sqrt{2}+2}}{4}\end{align*}[/latex]
Note
For greater accuracy, the denominators of fractions should be rational, rather than irrational numbers. The value of irrational numbers (such as [latex]\scriptsize \sqrt{2}[/latex]) can only be estimated, whereas the exact value of rational numbers is known. When we multiply by [latex]\scriptsize \displaystyle \frac{{\sqrt{2}}}{{\sqrt{2}}}[/latex]in the above example, we say that we are ‘rationalising the denominator’.
Example 1.2
Simplify the following trig expression without a calculator, leaving your answer in simplest surd form: [latex]\scriptsize \displaystyle \frac{{\cos {{{45}}^\circ}+\sin {{{45}}^\circ}}}{{\tan {{{45}}^\circ}}}[/latex].
Solution
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\cos {{{45}}^\circ}+\sin {{{45}}^\circ}}}{{\tan {{{45}}^\circ}}}&=\displaystyle \frac{{\displaystyle \frac{1}{{\sqrt{2}}}+\displaystyle \frac{1}{{\sqrt{2}}}}}{1}\\&=\displaystyle \frac{2}{{\sqrt{2}}}&& \text{Multiply by }\displaystyle \frac{{\sqrt{2}}}{{\sqrt{2}}}\text{ to rationalise the denominator}\\&=\displaystyle \frac{2}{{\sqrt{2}}}\times \displaystyle \frac{{\sqrt{2}}}{{\sqrt{2}}}\\&=\displaystyle \frac{{2\sqrt{2}}}{2}\end{align*}[/latex]
Example 1.3
Simplify the following trig expression without a calculator, leaving your answer in simplest surd form: [latex]\scriptsize \displaystyle \frac{{\sin {{{30}}^\circ}\cos {{{30}}^\circ}}}{{\tan {{{30}}^\circ}}}+\displaystyle \frac{{\sin {{{60}}^\circ}\cos {{{60}}^\circ}}}{{\tan {{{60}}^\circ}}}[/latex].
Solution
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\sin {{{30}}^\circ}\cos {{{30}}^\circ}}}{{\tan {{{30}}^\circ}}}+\displaystyle \frac{{\sin {{{60}}^\circ}\cos {{{60}}^\circ}}}{{\tan {{{60}}^\circ}}}\text{ }&=\displaystyle \frac{{\displaystyle \frac{1}{2}\times \displaystyle \frac{{\sqrt{3}}}{2}}}{{\displaystyle \frac{1}{{\sqrt{3}}}}}+\displaystyle \frac{{\displaystyle \frac{{\sqrt{3}}}{2}\times \displaystyle \frac{1}{2}}}{{\displaystyle \frac{{\sqrt{3}}}{1}}}\\&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{3}}}{4}}}{{\displaystyle \frac{1}{{\sqrt{3}}}}}+\displaystyle \frac{{\displaystyle \frac{{\sqrt{3}}}{4}}}{{\displaystyle \frac{{\sqrt{3}}}{1}}}\\&=\displaystyle \frac{{\sqrt{3}}}{4}\times \displaystyle \frac{{\sqrt{3}}}{1}+\displaystyle \frac{{\sqrt{3}}}{4}\times \displaystyle \frac{1}{{\sqrt{3}}}\\&=\displaystyle \frac{3}{4}+\displaystyle \frac{1}{4}\\&=1\end{align*}[/latex]
Exercise 1.1
Simplify the following trig expression without a calculator, leaving your answer in simplest surd form:
- [latex]\scriptsize {{\sin }}30^\circ+{{\tan }}60^\circ[/latex]
- [latex]\scriptsize \displaystyle \frac{{{{{\sin }}^\circ}60}}{{{{{\cos }}^\circ}60}}[/latex]
- [latex]\scriptsize {{\sin }^{2}}{{30}^\circ}+{{\cos }^{2}}{{30}^\circ}[/latex]
- [latex]\scriptsize \sqrt{\sin^2 45^\circ\cdot\cos^2 45^\circ }[/latex]
- [latex]\scriptsize \displaystyle \frac{{\sin {{{45}}^\circ}}}{{\cos {{{45}}^\circ}}}+\tan {{45}^\circ}[/latex]
The full solutions are at the end of the unit.
Finding special angles
In the previous section, we were asked to simplify expressions containing trig ratios of the special angles. If we discover that [latex]\scriptsize \sin \theta =\displaystyle \frac{1}{2}[/latex], for example, we can work in reverse to state that [latex]\scriptsize \theta ={{30}^\circ}[/latex].
Example 1.4
Given the following diagram, determine the values of [latex]\scriptsize \alpha[/latex] and [latex]\scriptsize \theta[/latex].
Solution
Let’s start with [latex]\scriptsize \theta[/latex] as our angle. With respect to [latex]\scriptsize \theta[/latex], we know that [latex]\scriptsize \cos \theta =\displaystyle \frac{{3\sqrt{3}}}{{6\sqrt{3}}}=\displaystyle \frac{1}{2}[/latex]. Therefore, [latex]\scriptsize \theta ={{60}^\circ}[/latex].
Because the angles inside a triangle are supplementary (they add up to [latex]\scriptsize {{180}^\circ}[/latex]), we know that [latex]\scriptsize \alpha ={{180}^\circ}-{{90}^\circ}-{{60}^\circ}={{30}^\circ}[/latex].
Exercise 1.2
- Determine the value of [latex]\scriptsize \theta[/latex] without a calculator:
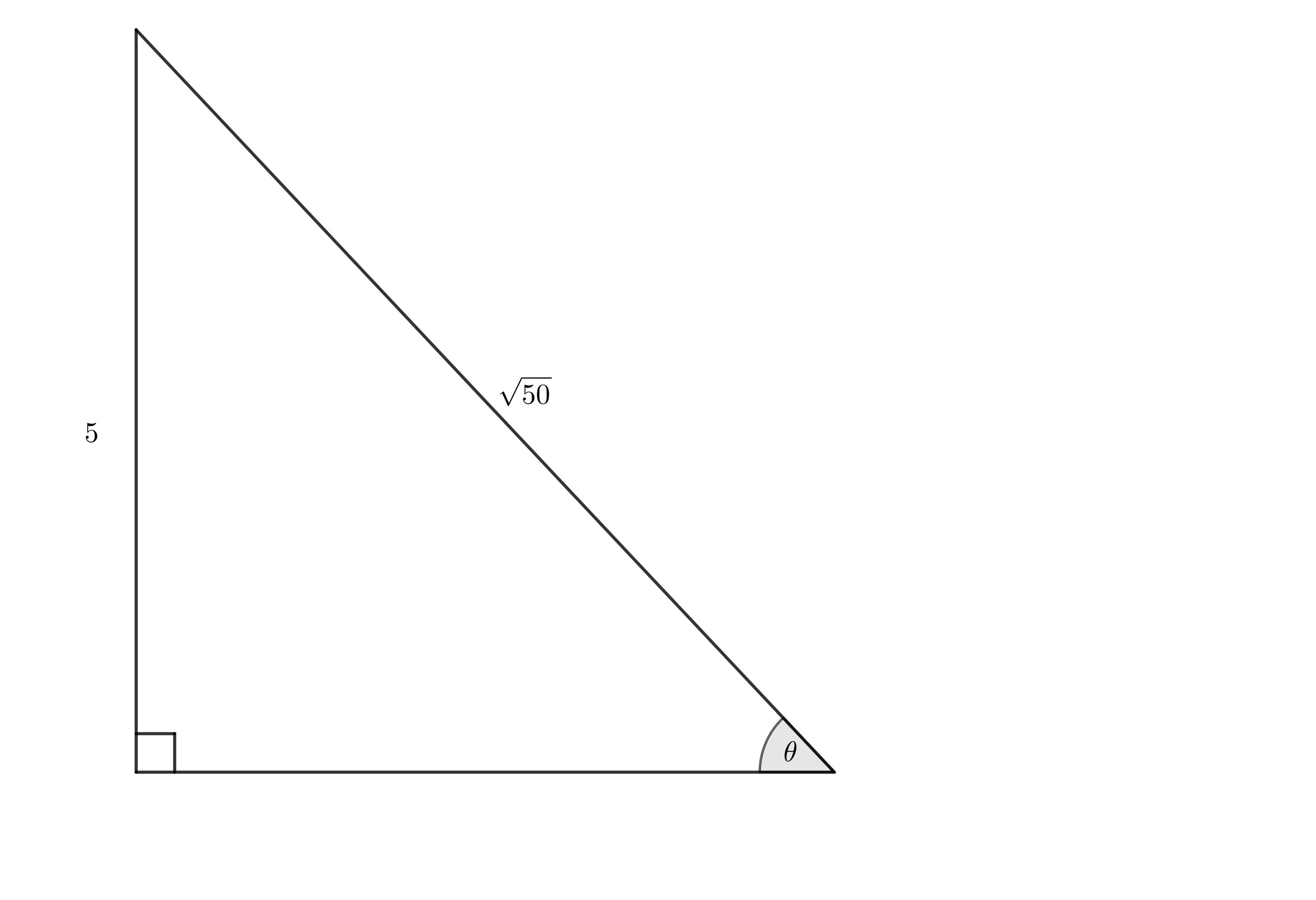
- Using the following diagram:
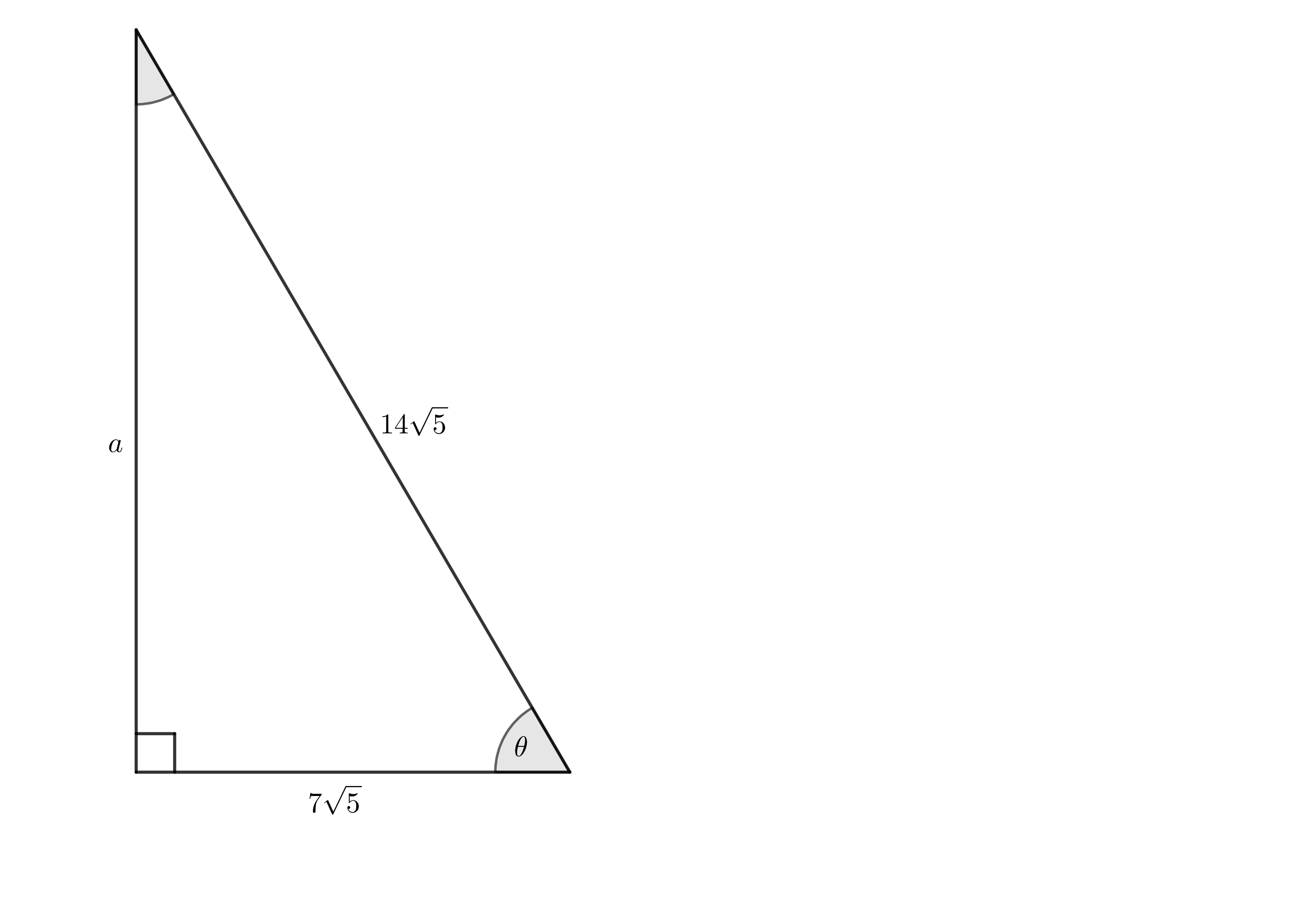
- Determine [latex]\scriptsize \theta[/latex] without a calculator.
- Find:
- [latex]\scriptsize \sin \theta[/latex]
- [latex]\scriptsize \tan \theta[/latex]
- Determine the length of [latex]\scriptsize a[/latex].
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- How to determine any of the basic trig ratios without a calculator if the angle involved is one of the special angles.
- How to determine the angle, if the sides of a triangle are in any of the special angle ratios.
Unit 1: Assessment
Suggested time to complete: 20 minutes
- Simplify the following trig expressions without a calculator, leaving your answer in simplest surd form:
- [latex]\scriptsize \sin {{45}^\circ}+\tan {{30}^\circ}[/latex]
- [latex]\scriptsize \sqrt{{1-{{{\sin }}^{2}}{{{45}}^\circ}}}[/latex]
- [latex]\scriptsize \displaystyle \frac{{{{{\sin }}^{2}}{{{30}}^\circ}}}{{{{{\tan }}^{2}}{{{60}}^\circ}\times {{{\cos }}^{2}}{{{60}}^\circ}}}[/latex]
- [latex]\scriptsize \text{sin6}{{\text{0}}^\circ}\text{cos3}{{\text{0}}^\circ}-\text{cos6}{{\text{0}}^\circ}\text{sin3}{{\text{0}}^\circ}\text{+ tan4}{{\text{5}}^\circ}[/latex]
- Prove, without a calculator, that [latex]\scriptsize \displaystyle \frac{{\sin {{{30}}^\circ}\cos {{{30}}^\circ}\tan {{{45}}^\circ}}}{{\sin {{{60}}^\circ}}}=\displaystyle \frac{1}{2}[/latex].
- Prove that [latex]\scriptsize \displaystyle \frac{{\sin {{{60}}^\circ}.\cos {{{60}}^\circ}}}{{\cos {{{45}}^\circ}.\sin {{{45}}^\circ}}}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex].
- Prove, without a calculator, that [latex]\scriptsize \sin ({{60}^\circ}).\tan {{60}^\circ}+\cos {{45}^\circ}.\sin {{45}^\circ}=2[/latex].
- Using the diagram:
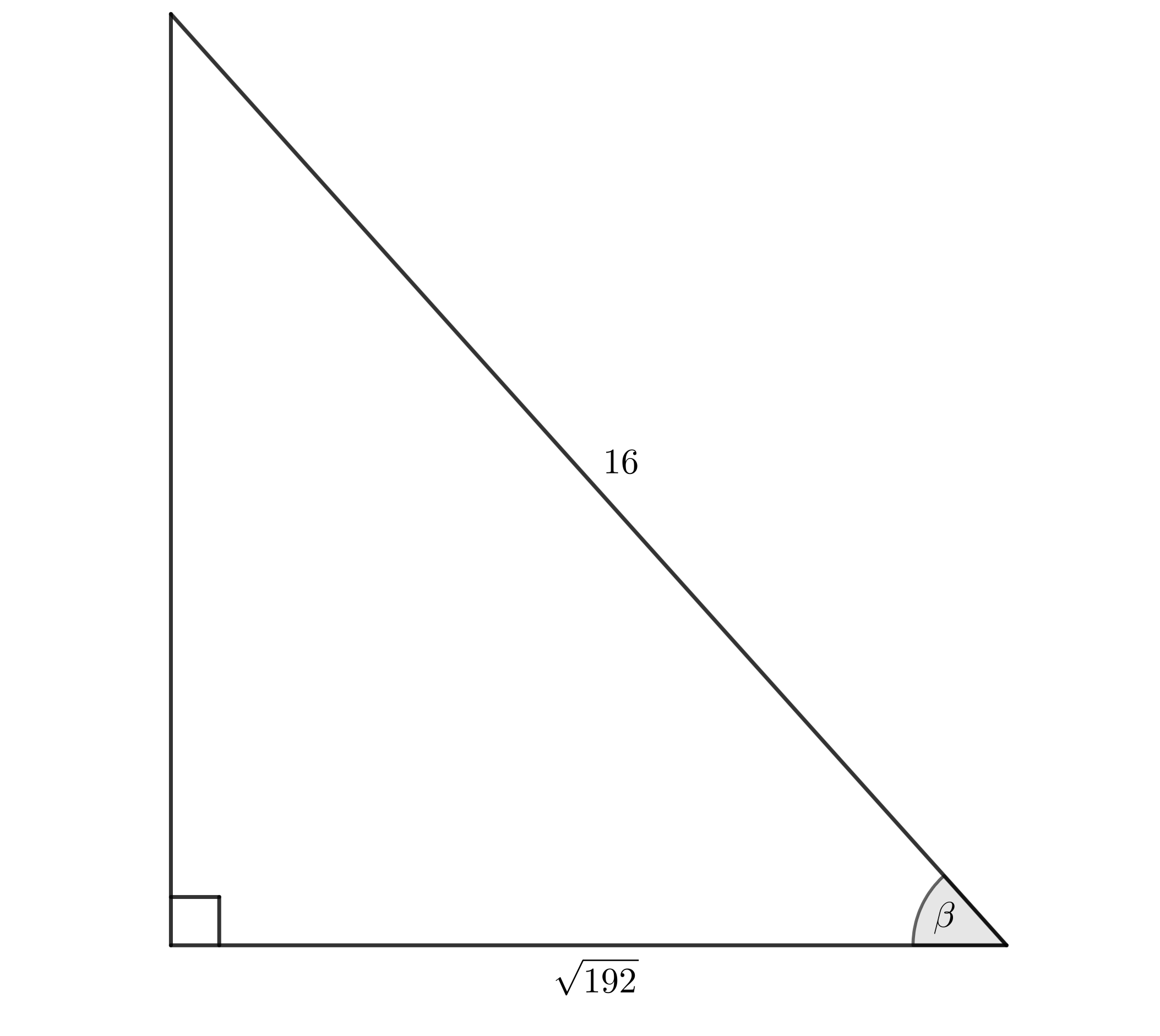
- Determine [latex]\scriptsize \beta[/latex] without using a calculator.
- Determine the value of [latex]\scriptsize \displaystyle \frac{{\tan \beta +\sin \beta }}{{{{{\cos }}^{2}}({{{90}}^\circ}-\beta )}}[/latex] without using a calculator.
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- .
[latex]\scriptsize \begin{align*}\sin 30{}^\circ +\tan 60{}^\circ&=\displaystyle \frac{1}{2}+\displaystyle \frac{{\sqrt{3}}}{1}\\&=\displaystyle \frac{{1+2\sqrt{3}}}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{{{{\sin }}}60^\circ}}{{{{{\cos }}}60^\circ}}&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{3}}}{2}}}{{\displaystyle \frac{1}{2}}}\\&=\displaystyle \frac{{\sqrt{3}}}{2}\times \displaystyle \frac{2}{1}\\&=\sqrt{3}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{\sin }^{2}}{{30}^\circ}+{{\cos }^{2}}{{30}^\circ}&={{\left( {\displaystyle \frac{1}{2}} \right)}^{2}}+{{\left( {\displaystyle \frac{{\sqrt{3}}}{2}} \right)}^{2}}\\&=\displaystyle \frac{1}{4}+\displaystyle \frac{3}{4}\\&=1\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\sqrt{\sin^2 45^\circ\cdot\cos^2 45^\circ }&=\sqrt{{{{{\left( {\displaystyle \frac{1}{{\sqrt{2}}}} \right)}}^{2}}\cdot {{{\left( {\displaystyle \frac{1}{{\sqrt{2}}}} \right)}}^{2}}}}\\&=\sqrt{{\displaystyle \frac{1}{2}\cdot \displaystyle \frac{1}{2}}}\\&=\sqrt{{\displaystyle \frac{1}{4}}}\\&=\pm \displaystyle \frac{1}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align}\displaystyle \frac{\sin 45{}^\circ }{\cos 45{}^\circ }+\tan 45{}^\circ & =\displaystyle \frac{\displaystyle \frac{1}{\sqrt{2}}}{\displaystyle \frac{1}{\sqrt{2}}}+1 \\ & =2 \\ \end{align}[/latex]
Exercise 1.2
- .
[latex]\scriptsize \begin{align*}\sin \theta & =\displaystyle \frac{5}{{\sqrt{{50}}}}\\&=\displaystyle \frac{5}{{\sqrt{{25\times 2}}}}\\&=\displaystyle \frac{5}{{5\sqrt{2}}}\\&=\displaystyle \frac{1}{{\sqrt{2}}}\\\therefore \theta & ={{45}^\circ}\end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*}\cos \theta & =\displaystyle \frac{{7\sqrt{5}}}{{14\sqrt{5}}}=\displaystyle \frac{1}{2}\\\therefore \theta & ={{60}^\circ}\end{align*}[/latex] - .
- [latex]\scriptsize \sin \theta =\sin {{60}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}[/latex]
- [latex]\scriptsize \tan \theta =\tan {{60}^\circ}=\displaystyle \frac{{\sqrt{3}}}{1}[/latex]
- .
[latex]\scriptsize \begin{align*}\tan \theta & =\displaystyle \frac{{\sqrt{3}}}{1}=\displaystyle \frac{a}{{7\sqrt{5}}}\\\therefore a & =7\sqrt{3}\sqrt{5}\\ & =7\sqrt{{15}}\end{align*}[/latex]
Note: You could also have used [latex]\scriptsize \sin \theta =\sin {{60}^\circ}=\displaystyle \frac{{\sqrt{3}}}{2}=\displaystyle \frac{a}{{14\sqrt{5}}}[/latex], etc.
- .
Unit 1: Assessment
- .
- .
[latex]\scriptsize \begin{align*}\sin 45{}^\circ +\tan 30{}^\circ&=\displaystyle \frac{1}{{\sqrt{2}}}+\displaystyle \frac{1}{{\sqrt{3}}}\\&=\displaystyle \frac{{\sqrt{3}+\sqrt{2}}}{{\sqrt{2}\sqrt{3}}}\\&=\displaystyle \frac{{\sqrt{3}+\sqrt{2}}}{{\sqrt{2}\sqrt{3}}}\times \displaystyle \frac{{\sqrt{2}\sqrt{3}}}{{\sqrt{2}\sqrt{3}}}\\&=\displaystyle \frac{{3\sqrt{2}+2\sqrt{3}}}{6}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\sqrt{{1-{{{\sin }}^{2}}{{{45}}^\circ}}}&=\sqrt{{1-{{{\left( {\displaystyle \frac{1}{{\sqrt{2}}}} \right)}}^{2}}}}\\&=\sqrt{{1-\displaystyle \frac{1}{2}}}\\&=\sqrt{{\displaystyle \frac{1}{2}}}\\&=\displaystyle \frac{1}{{\sqrt{2}}}\quad \text{Multiply by }\displaystyle \frac{{\sqrt{2}}}{{\sqrt{2}}}\\&=\displaystyle \frac{{\sqrt{2}}}{2}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{{{{\sin }}^{2}}{{{30}}^\circ}}}{{{{{\tan }}^{2}}{{{60}}^\circ}\times {{{\cos }}^{2}}{{{60}}^\circ}}}&=\displaystyle \frac{{{{{\left( {\displaystyle \frac{1}{2}} \right)}}^{2}}}}{{{{{\left( {\displaystyle \frac{{\sqrt{3}}}{1}} \right)}}^{2}}\times {{{\left( {\displaystyle \frac{1}{2}} \right)}}^{2}}}}\\&=\displaystyle \frac{{\displaystyle \frac{1}{4}}}{{\displaystyle \frac{3}{1}\times \displaystyle \frac{1}{4}}}\\&=\displaystyle \frac{{\displaystyle \frac{1}{4}}}{{\displaystyle \frac{3}{4}}}\\&=\displaystyle \frac{1}{4}\times \displaystyle \frac{4}{3}\\&=\displaystyle \frac{1}{3}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\text{sin6}{{\text{0}}^\circ}\text{cos3}{{\text{0}}^\circ}-\text{cos6}{{\text{0}}^\circ}\text{sin3}{{\text{0}}^\circ}\text{+ tan4}{{\text{5}}^\circ}\text{ }&=\displaystyle \frac{{\sqrt{3}}}{2}\centerdot \displaystyle \frac{{\sqrt{3}}}{2}-\displaystyle \frac{1}{2}\centerdot \displaystyle \frac{1}{2}+1\\&=\displaystyle \frac{3}{4}-\displaystyle \frac{1}{4}+1\\&=\displaystyle \frac{1}{2}+1\\&=\displaystyle \frac{3}{2}\end{align*}[/latex]
- .
- .
[latex]\scriptsize \begin{align*} \text{LHS}&=\displaystyle \frac{\sin30^\circ\cos30^\circ\tan45^\circ}{\sin60^\circ}\\ &=\displaystyle \frac{\displaystyle \frac{1}{2}\times\displaystyle \frac{\sqrt{3}}{2}\times1}{\displaystyle \frac{\sqrt{3}}{2}}\\ &=\displaystyle \frac{\displaystyle \frac{\sqrt{3}}{4}}{\displaystyle \frac{\sqrt{3}}{2}}\\ &=\displaystyle \frac{\sqrt{3}}{4}\times\displaystyle \frac{2}{\sqrt{3}}\\ &=\displaystyle \frac{1}{2}\\ &=\text{RHS} \end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\text{LHS}&=\displaystyle \frac{{\sin {{{60}}^\circ}.\cos {{{60}}^\circ}}}{{\cos {{{45}}^\circ}.\sin {{{45}}^\circ}}}\\&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{3}}}{2}\cdot \displaystyle \frac{1}{2}}}{{\displaystyle \frac{1}{{\sqrt{2}}}\cdot \displaystyle \frac{1}{{\sqrt{2}}}}}\\&=\displaystyle \frac{{\displaystyle \frac{{\sqrt{3}}}{4}}}{{\displaystyle \frac{1}{2}}}\\&=\displaystyle \frac{{\sqrt{3}}}{4}\times \displaystyle \frac{2}{1}\\&=\displaystyle \frac{{\sqrt{3}}}{2}=\text{RHS}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\text{LHS}&=\sin {{60}^\circ}.\tan {{60}^\circ}+\cos {{45}^\circ}.\sin {{45}^\circ}\\&=\displaystyle \frac{{\sqrt{3}}}{2}\cdot \displaystyle \frac{{\sqrt{3}}}{1}+\displaystyle \frac{1}{{\sqrt{2}}}\cdot \displaystyle \frac{1}{{\sqrt{2}}}\\&=\displaystyle \frac{3}{2}+\displaystyle \frac{1}{2}\\&=2=\text{RHS}\end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*}\cos \beta & =\displaystyle \frac{{\sqrt{{192}}}}{{16}}=\displaystyle \frac{{\sqrt{{64\cdot 3}}}}{{16}}=\displaystyle \frac{{8\sqrt{3}}}{{16}}=\displaystyle \frac{{\sqrt{3}}}{2}\\\therefore \beta & ={{30}^\circ}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}\displaystyle \frac{{\tan \beta +\sin \beta }}{{{{{\cos }}^{2}}({{{90}}^\circ}-\beta )}}&=\displaystyle \frac{{\tan {{{30}}^\circ}+\sin {{{30}}^\circ}}}{{{{{\cos }}^{2}}{{{60}}^\circ}}}\\&=\displaystyle \frac{{\displaystyle \frac{1}{{\sqrt{3}}}+\displaystyle \frac{1}{2}}}{{{{{\left( {\displaystyle \frac{1}{2}} \right)}}^{2}}}}\\&=\displaystyle \frac{{\displaystyle \frac{{2+\sqrt{3}}}{{2\sqrt{3}}}}}{{\displaystyle \frac{1}{4}}}\\&=\displaystyle \frac{{2+\sqrt{3}}}{{2\sqrt{3}}}\times \displaystyle \frac{4}{1}\\&=\displaystyle \frac{{8+4\sqrt{3}}}{{2\sqrt{3}}}\quad \text{Multiply by }\displaystyle \frac{{\sqrt{3}}}{{\sqrt{3}}}\\&=\displaystyle \frac{{8\sqrt{3}+12}}{6}\\&=\displaystyle \frac{{4\left( {2\sqrt{3}+3} \right)}}{6}\\&=\displaystyle \frac{{2\left( {2\sqrt{3}+3} \right)}}{3}\end{align*}[/latex]
- .
Media Attributions
- figure1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- 30degree © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- 60degree © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- 45degree © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.2Q1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise1.2Q2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- assessmentQ5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
