Space, shape and measurement: Calculate the surface area and volume of two- and three-dimensional shapes
Unit 1: Finding the volume of 3-D shapes
Natashia Bearam-Edmunds
Unit outcomes
By the end of this unit you will be able to:
- Apply the appropriate formulae to find the volume of:
- right pyramids (with square, equilateral triangle or regular hexagonal bases)
- right cones
- spheres.
- Determine and calculate the volume of combinations of these geometric objects.
What you should know
Before you start this unit, make sure you can:
- calculate perimeter and area of two-dimensional shapes, and surface area and volume of prisms. You can revise this in level 2 subject outcome 3.2.
Introduction
Volume is the amount of three-dimensional (3-D) space taken up by a solid, liquid or gas. Volume is measured in cubes or cubic units. The terms volume and capacity are often used to mean the same thing but there is a slight difference.
Capacity is the amount of liquid or other substance a container can hold. Capacity is only used in relation to containers. A can of cooldrink has volume, as it takes up a certain amount of space and has capacity to be filled with liquid. So, when you are filling a container with liquid or other substances you are working with capacity.
We saw in level 2 that we find the volume of right prisms and cylinders by multiplying the area of the base by the height of the 3-D shape. Now, we will find the volume of right pyramids, cones and spheres.
Pyramids
Pyramids have only one polygon base and the side faces are triangles that meet at a vertex called the apex. There are many types of pyramids, and they are named after the shape of their base. We call a pyramid a “right pyramid” if the line between the apex and the centre of the base is perpendicular to the base.
For example, in the square based pyramid the base is a square and the sides are isosceles triangles, which meet at the apex.
A tetrahedron or triangular pyramid has a triangular base and sides. It is made up of four equilateral triangles, has six edges and four vertices.
A hexagonal pyramid has a hexagonal base and six isosceles triangle faces as its sides.
To find the volume of a pyramid we divide the area of its base by three and multiply by its height.
[latex]\scriptsize \displaystyle \text{Volume of pyramid}=\displaystyle \frac{1}{3}\text{area of base}\times \text{height}[/latex]
Example 1.1
Find the volume of a regular square pyramid with base sides [latex]\scriptsize \displaystyle \text{5 cm}[/latex] and altitude [latex]\scriptsize \displaystyle 10\text{ cm}[/latex].
Solution
First, we find the area of the base, which is a square.
[latex]\scriptsize \displaystyle \begin{align*}\text{Area of square base}&=5\text{ cm}\times 5\text{ cm}\\&=25\text{ c}{{\text{m}}^{2}}\end{align*}[/latex]
Altitude is the same as the height. Now we multiply the area of the base by the height of the pyramid and divide by three to find its volume.
[latex]\scriptsize \displaystyle \begin{align*}\text{Volume }&=\displaystyle \frac{1}{3}(25\text{ c}{{\text{m}}^{2}})\times 10\text{ cm}\\&=83.3\text{ c}{{\text{m}}^{3}}\end{align*}[/latex]
Example 1.2
A paperweight is in the shape of a hexagonal pyramid with base sides [latex]\scriptsize \displaystyle \text{12 cm}[/latex] and a vertical height of [latex]\scriptsize \displaystyle \text{15 cm}[/latex]. Find the volume of the paperweight.
Solution
The area of a hexagon is given by: [latex]\scriptsize \displaystyle \frac{{3\sqrt{3}}}{2}{{\text{s}}^{2}}[/latex].
[latex]\scriptsize \displaystyle \begin{align*}\text{Volume }&=\displaystyle \frac{1}{3}\left[ {\displaystyle \frac{{3\sqrt{3}}}{2}{{{(12\text{ cm})}}^{2}}} \right]\times 15\text{ cm}\\&=1\text{ }870.61\text{ c}{{\text{m}}^{3}}\end{align*}[/latex]
Exercise 1.1
- The figure below shows a triangular pyramid shaped container with altitude of [latex]\scriptsize 2\text{ m}[/latex]. The side length is [latex]\scriptsize \text{3 m}[/latex] and the height of the triangle is [latex]\scriptsize 2.6\text{ m}[/latex].
- Find the volume of the container.
- The container must be packed into a box. If the box has a volume of [latex]\scriptsize 2.5\text{ }{{\text{m}}^{3}}[/latex] will the container fit into the box?
- We need to fit square pyramid ornaments with base side of [latex]\scriptsize 10\text{ mm}[/latex] and height of [latex]\scriptsize \text{5 mm}[/latex] into a rectangular box to be transported from Cape Town to Johannesburg. If the box has a length of [latex]\scriptsize 25\text{ cm}[/latex], a breadth of [latex]\scriptsize 15\text{ cm}[/latex]and a height of [latex]\scriptsize 5\text{ cm}[/latex], how many ornaments will fit into the box?
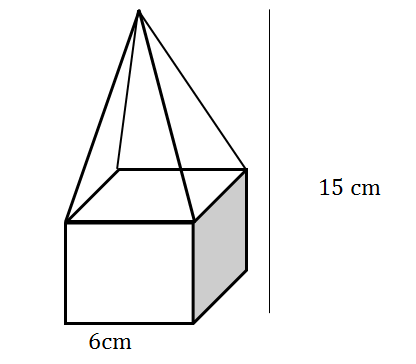
- The solid below is made of a cube and a square pyramid. Determine the volume of the shape.
The full solutions are at the end of the unit.
Cones
Cones are similar to pyramids except that their bases are circles instead of polygons.
We find the volume of a cone using a similar formula to that for right pyramids.
[latex]\scriptsize \displaystyle \begin{align*}\text{Volume of cone}&=\displaystyle \frac{1}{3}\text{area of base}\times \text{height of cone}\\ &= \displaystyle \frac{1}{3}\pi {{r}^{2}}H\end{align*}[/latex]
Example 1.3
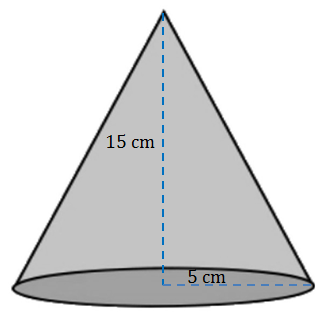
Find the volume of the following cone (correct to 1 decimal place).
 Solution
Solution
First, find the area of the base.
[latex]\scriptsize \displaystyle \begin{align*}A&=\pi {{r}^{2}}\\&=\pi {{(5\text{ cm)}}^{2}}\\&=25\pi \text{ c}{{\text{m}}^{2}}\end{align*}[/latex]
Next, calculate the volume of the cone.
[latex]\scriptsize \displaystyle \begin{align*}V&=\displaystyle \frac{1}{3}\text{area of base}\times \text{height of cone}\\ &= \displaystyle \frac{1}{3}(25\pi )\times 15\text{ }\\& =125 \pi \text{ c}{{\text{m}}^{3}}\\&=392.7\text{ c}{{\text{m}}^{3}}\end{align*}[/latex]
Spheres
Spheres are solids that are perfectly round and look the same from any direction.
Note
Watch this video to see an example of calculating the volume of a sphere.
Example 1.4
A world globe is in the shape of a sphere with radius of [latex]\scriptsize 12\text{ cm}[/latex]. Find its volume correct to one decimal place.

Solution
[latex]\scriptsize \begin{align*}{{V}_{{\text{sphere}}}}&=\displaystyle \frac{4}{3}\pi {{r}^{3}}\\&=\displaystyle \frac{4}{3}\pi {{(12)}^{3}}\\&=7238.2\text{ c}{{\text{m}}^{3}}\end{align*}[/latex]
Exercise 1.2
- Tom has [latex]\scriptsize 20[/latex] new marbles. If the marbles are spherical in shape and each one has a diameter of [latex]\scriptsize 4\text{ mm}[/latex] what is the total volume of Tom’s marbles?
- The vertical height of a cone is [latex]\scriptsize 7[/latex] units and the slant height is [latex]\scriptsize 7.28[/latex] units; the radius of the cone is [latex]\scriptsize 2[/latex] units. Calculate the volume of the cone. Round your answer off to two decimal places.
- An open rectangular fish tank, [latex]\scriptsize 80\text{ cm}[/latex] long, [latex]\scriptsize \text{35 cm}[/latex] wide and [latex]\scriptsize \text{45 cm}[/latex] high, is full to the top with water. John puts [latex]\scriptsize 30[/latex] marbles, each with a diameter of [latex]\scriptsize \text{1 cm}[/latex], into the tank resulting in some of the water spilling out of the fish tank.
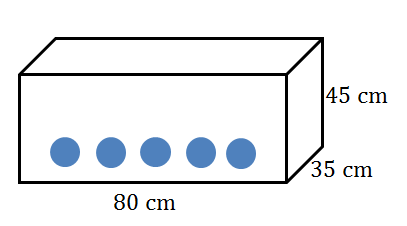
- Determine the initial volume of the water in the tank.
- Calculate the volume of one marble.
- Calculate the volume of the water that spilled out of the tank after all the marbles have been added in.
The full solutions are at the end of the unit.
Summary
In this unit you have learnt the following:
- How to find the volume of right pyramids.
- How to find the volume of spheres.
- How to find the volume of cones.
Unit 1: Assessment
Suggested time to complete: 30 minutes
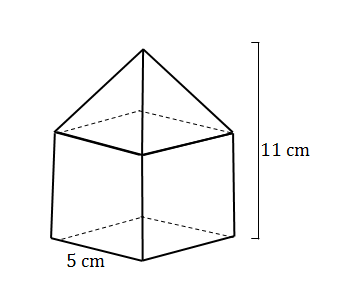
- A solid is made up of a cube and a square pyramid. Find its volume if the height of the solid is [latex]\scriptsize 11\text{ cm}[/latex] and the sides of the base are [latex]\scriptsize \text{5 cm}[/latex].
- An insecticide company has mistakenly manufactured cube-shaped moth balls instead of spherical-shaped moth balls. The cube-shaped moth balls have a side length of [latex]\scriptsize 16\text{ mm}[/latex]. The spherical-shaped moth balls must have a diameter of [latex]\scriptsize \text{20 mm}[/latex].
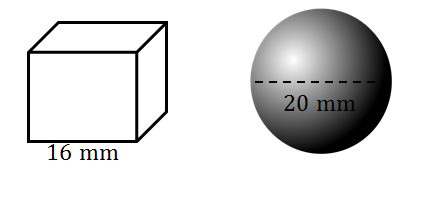
Calculate:- The volume of each cube-shaped moth ball.
- The volume of one spherical-shaped moth ball.
- The extra amount of material required if the original order was for [latex]\scriptsize 2[/latex] million [latex]\scriptsize \displaystyle (2\text{ }000\text{ }000)[/latex]spherical moth balls.
- A solid golden sphere with a diameter of [latex]\scriptsize \displaystyle 14\text{ mm}[/latex] is to be melted and cast into a piece of jewellery. The piece of jewellery is in the shape of a right pyramid with a square base. The square pyramid has a vertical height of [latex]\scriptsize \displaystyle 10\text{ mm}[/latex] and a side length of [latex]\scriptsize \displaystyle 20\text{ mm}[/latex]. Calculate the excess gold (gold left over) after the piece of jewellery has been made.
The full solutions are at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- .
- .
[latex]\scriptsize \begin{align*}V&=\displaystyle \frac{1}{3}\text{area of base}\times \text{height}\\ \therefore V&= \displaystyle \frac{1}{3}\left( {\displaystyle \frac{1}{2}(3)\times 2.6} \right)\times 2\\&=2.6\text{ }{{\text{m}}^{3}}\end{align*}[/latex] - The container will not fit into the box since its volume of [latex]\scriptsize 2.7\text{ }{{\text{m}}^{3}}[/latex] is greater than the volume of the box.
- .
- Remember to convert lengths from millimetres to centimetres.
[latex]\scriptsize \displaystyle \begin{align*}{{V}_{{\text{pyramid}}}}&=\displaystyle \frac{1}{3}\text{area of base}\times \text{height}\\&=\displaystyle \frac{1}{3}(1\text{ cm}\times 1\text{ cm})\times 0.5\text{ cm}\\ &= \displaystyle \frac{1}{6}\text{ c}{{\text{m}}^{3}}\end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}{{V}_{{\text{box}}}}&=25\text{ cm}\times 15\text{ cm}\times 5\text{ cm}\\ &= \text{ 1875 c}{{\text{m}}^{3}}\end{align*}[/latex]
Number of ornaments:
[latex]\scriptsize \begin{align*}\displaystyle \frac{{{{V}_{{\text{box}}}}}}{{{{V}_{{\text{ornaments}}}}}}&=1875\div \displaystyle \frac{1}{6}\\&=11\text{ }250\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{V}_{{\text{cube}}}}&={{s}^{3}}\\ &={{6}^{3}}\\&=216\text{ c}{{\text{m}}^{3}}\\ {{V}_{{\text{pyramid}}}}&=\displaystyle \frac{1}{3}{{\left( 6 \right)}^{2}}\times (15-6)\\ &=108\text{ c}{{\text{m}}^{3}}\\ \text{Total volume:}\text{ }\\ 216\text{ c}{{\text{m}}^{3}}+108\text{ c}{{\text{m}}^{3}}&=324\text{ c}{{\text{m}}^{3}} \end{align*}[/latex]
Exercise 1.2
- Remember to divide [latex]\scriptsize 4\text{ mm}[/latex] by two to get the length of the radius.
[latex]\scriptsize \displaystyle \begin{align*}V&=\displaystyle \frac{4}{3}\pi {{r}^{3}}\\&=\displaystyle \frac{4}{3}\pi {{(2)}^{3}}\\&=\displaystyle \frac{{32}}{3}\pi \text{ m}{{\text{m}}^{3}}\text{ volume of each marble}\\ \text{Total volume:}\\\displaystyle \frac{{32}}{3}\pi \text{ m}{{\text{m}}^{3}}\times 20&=670.2\text{ m}{{\text{m}}^{3}}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\text{Volume of cone}&=\displaystyle \frac{1}{3}\text{area of base}\times \text{height of cone}\\ &= \displaystyle \frac{1}{3}\pi {{(2)}^{2}}\times 7\\&=29.32\text{ cubic units}\end{align*}[/latex] - .
- Volume of the water in the tank:
[latex]\scriptsize \begin{align*}V&=l\times b\times h\\&=80\text{ cm}\times 35\text{ cm}\times 45\text{ cm}\\&=126\text{ }000\text{ c}{{\text{m}}^{3}}\end{align*}[/latex] - Volume of one marble:
Radius is [latex]\scriptsize 0.5\text{ cm}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}V&=\displaystyle \frac{4}{3}\pi {{r}^{3}}\\&=\displaystyle \frac{4}{3}\pi {{(0.5\text{ cm})}^{3}}\\&=\displaystyle \frac{1}{6}\pi \text{ c}{{\text{m}}^{3}}\\&=0.52\text{ c}{{\text{m}}^{3}}\end{align*}[/latex] - Total volume of marbles will give the amount of water that spilled over:
[latex]\scriptsize \displaystyle \displaystyle \frac{1}{6}\pi \text{ c}{{\text{m}}^{3}}\times 30=15.71\text{ c}{{\text{m}}^{3}}[/latex]
- Volume of the water in the tank:
Unit 1: Assessment
- .
[latex]\scriptsize \begin{align*}{{V}_{{\text{cube}}}}&={{s}^{3}}\\&={{5}^{3}}\\&=125\text{ c}{{\text{m}}^{3}}\\{{V}_{{\text{pyramid}}}}&=\displaystyle \frac{1}{3}{{\left( 5 \right)}^{2}}\times (11-5)\\&=50\text{ c}{{\text{m}}^{3}}\\\text{Total volume:}\text{ }\\125\text{ c}{{\text{m}}^{3}}+50\text{ c}{{\text{m}}^{3}}&=175\text{ c}{{\text{m}}^{3}}\end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*}{{V}_{{\text{cube}}}}&={{s}^{3}}\\&={{16}^{3}}\\&=4\text{ }096\text{ m}{{\text{m}}^{3}}\end{align*}[/latex] - .
Diameter of [latex]\scriptsize \text{20 mm}[/latex][latex]\scriptsize \therefore[/latex]radius of [latex]\scriptsize 10\text{ mm}[/latex].
[latex]\scriptsize \displaystyle \begin{align*}V&=\displaystyle \frac{4}{3}\pi {{r}^{3}}\\&=\displaystyle \frac{4}{3}\pi {{(10)}^{3}}\\&=\displaystyle \frac{{4\text{ }000}}{3}\pi \text{ m}{{\text{m}}^{3}}\\&=4188.79\text{ m}{{\text{m}}^{3}}\text{ correct to 2 decimal places}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle 2\text{ }000\text{ }000\times (\displaystyle \frac{{4000}}{3}\pi \text{ m}{{\text{m}}^{3}}-4\text{ }096\text{ m}{{\text{m}}^{3}})=185\text{ }580\text{ }409\text{ m}{{\text{m}}^{3}}[/latex]
- .
- .
[latex]\scriptsize \displaystyle \begin{align*}{{V}_{{\text{sphere}}}}&=\displaystyle \frac{4}{3}\pi {{r}^{3}}\\&=\displaystyle \frac{4}{3}\pi {{(7)}^{3}}\\&=\displaystyle \frac{{1\text{ 372}}}{3}\pi \text{ m}{{\text{m}}^{3}}\\\\{{V}_{{\text{pyramid}}}}&=\displaystyle \frac{1}{3}{{(20)}^{2}}\times 10\\&=\displaystyle \frac{{4\text{ }000}}{3}\text{ m}{{\text{m}}^{3}}\\\text{Excess gold:}\\\displaystyle \frac{{1\text{ 372}}}{3}\pi \text{ m}{{\text{m}}^{3}}-\displaystyle \frac{{4\text{ }000}}{3}\text{ m}{{\text{m}}^{3}}&=103.42\text{ m}{{\text{m}}^{3}}\end{align*}[/latex]
Media Attributions
- Square pyramid © kids-flashcards.com is licensed under a All Rights Reserved license
- triangular pyramid © kids-flashcards.com is licensed under a All Rights Reserved license
- hexagonal pyramid © kids-flashcards.com is licensed under a All Rights Reserved license
- Ex 1.1 Q1 © kids-flashcards.com is licensed under a All Rights Reserved license
- Ex 1.1 Q3 © kids-flashcards.com is licensed under a All Rights Reserved license
- cone © kids-flashcards.com is licensed under a All Rights Reserved license
- Example 1.3 © kids-flashcards.com is licensed under a All Rights Reserved license
- Example 1.4 © kids-flashcards.com is licensed under a All Rights Reserved license
- Ex 1.2 Q3 © DHET is licensed under a CC BY (Attribution) license
- Assess Q1 © DHET is licensed under a CC BY (Attribution) license
- Assess Q2 © DHET is licensed under a CC BY (Attribution) license
